有摩天大楼和鸡蛋的任务-不是牛顿的垃圾箱？

实际上，他是最。 但是首先是第一件事。

问题陈述

我精通python，解决了Codewars上的所有问题。 我遇到了一个关于摩天大楼和鸡蛋的著名任务。 唯一的区别是源数据不是100层和2个鸡蛋，而是更多。
给定：N个鸡蛋，M试图扔它们，无尽的摩天大楼。

定义：您可以扔鸡蛋而不破裂的最大地板。 鸡蛋在真空中呈球形，如果其中一个鸡蛋没有破裂，例如从第99层跌落，那么其他鸡蛋也将承受从所有楼层跌落不到百分之一的跌落。

0 <= N，M <= 20,000。
两次测试的运行时间为12秒。

寻找解决方案

我们需要编写一个函数高度（n，m），它将返回给定n，m的层数。 由于它经常被提及，并且每次您编写“高度”惰性时，除代码外，所有地方，我都将其指定为f（n，m）。

让我们从零开始。 显然，如果没有鸡蛋或尝试扔鸡蛋，则无法确定，答案为零。 f（0，m）= 0，f（n，0）= 0。

假设有一个鸡蛋，并且有10次尝试。您可以冒险冒险将其丢到第100层，但是一旦失败，您将无法确定其他任何东西，因此从第一层开始并在每次掷出后升上一层是更合乎逻辑的，直到尝试或鸡蛋结束。 如果鸡蛋没有失败，您可以获得的最大底数是地板号10。f（1，m）= m

拿第二个鸡蛋，再尝试10个。现在，那么您可以乘以百分之一的机会吗？ 如果破裂，将再尝试9次，至少可以通过9层。 因此，也许您需要冒险的不是第100个，而是第10个？ 是合乎逻辑的。 然后，如果成功，将保留2个鸡蛋和9个尝试。 打个比方，现在您需要再升9层。 有了一系列的成功-另外8、7、6、5、4、3、2和1。总计，我们位于第55层，拥有两个完整的鸡蛋，而且没有尝试。 答案是算术级数的前M个成员与第一个成员1和步骤1的总和。f（2，m）=（m * m + m）/ 2 。 同样清楚的是，在每个步骤中都调用了函数f（1，m），但这还不准确。

继续三个鸡蛋和十个尝试。 如果未成功进行第一掷，则从下面覆盖2个鸡蛋并进行9次尝试的地板，这意味着第一掷必须从地板f（2，9）+ 1进行。然后，如果成功，我们将获得3个鸡蛋9次尝试。 对于第二次尝试，您需要再上一层f（2.8）+ 1层楼。 依此类推，直到手上剩下3个鸡蛋和3个尝试。 然后是时候考虑一​​下N = M的情况了，这时蛋的数量与尝试的数量一样。


让我们回到f（3，10）。 实际上，每一步都归结为总和f（2，m-1）-发生故障时可以确定的楼层数，单位和f（3，m-1）-成功时可以确定的楼层数。 很明显，随着鸡蛋数量和尝试次数的增加，一切都不太可能改变。 f（n，m）= f（n-1，m-1）+ 1 + f（n，m-1） 。 这是可以用代码实现的通用公式。

from functools import lru_cache @lru_cache() def height(n,m): if n==0 or m==0: return 0 elif n==1: return m elif n==2: return (m**2+m)/2 elif n>=m: return 2**n-1 else: return height(n-1,m-1)+1+height(n,m-1) 

当然，之前我踩到了非记忆递归函数，发现f（10，40）花费了将近40秒的时间来调用它自己-97806983.但是记忆也仅在初始时间间隔内保存。 如果f（200,400）在0.8秒内执行，则f（200，500）在31秒内已经存在。 有趣的是，使用％timeit衡量运行时时，结果远不及实际情况。 显然，该函数的第一次运行花费大部分时间，而其余的仅使用其记忆化的结果。 说谎，公然的谎言和统计数据。

无需递归，我们可以进一步看

因此，例如，在测试中，出现了f（9477，10000），但我可怜的f（200，500）在合适的时间不再合适。 因此，还有另一种解决方案，无需递归，我们将继续进行搜索。 我通过对带有某些参数的函数调用进行计数来补充代码，以查看其最终分解为什么。 经过10次尝试，获得了以下结果：

f（3.10）= 7 + 1 * f（2.9）+ 1 * f（2.8）+ 1 * f（2.7）+ 1 * f（2.6）+ 1 * f（2 ，5）+ 1 * f（2,4）+ 1 * f（2,3）+ 1 * f（3,3）
f（4.10）= 27 + 1 * f（2.8）+ 2 * f（2.7）+ 3 * f（2.6）+ 4 * f（2.5）+ 5 * f（2 ，4）+ 6 * f（2,3）+ 6 * f（3,3）+ 1 * f（4,4）
f（5.10）= 55 + 1 * f（2.7）+ 3 * f（2.6）+ 6 * f（2.5）+ 10 * f（2.4）+ 15 * f（2 ，3）+ 15 * f（3.3）+ 5 * f（4.4）+ 1 * f（5.5）
f（6.10）= 69 + 1 * f（2.6）+ 4 * f（2.5）+ 10 * f（2.4）+ 20 * f（2.3）+ 20 * f（3 ，3）+ 10 * f（4.4）+ 4 * f（5.5）+ 1 * f（6.6）
f（7,10）= 55 + 1 * f（2,5）+ 5 * f（2,4）+ 15 * f（2,3）+ 15 * f（3,3）+ 10 * f（4 ，4）+ 6 * f（5.5）+ 3 * f（6.6）+ 1 * f（7.7）
f（8,10）= 27 + 1 * f（2,4）+ 6 * f（2,3）+ 6 * f（3,3）+ 5 * f（4,4）+ 4 * f（5 ，5）+ 3 * f（6.6）+ 2 * f（7.7）+ 1 * f（8.8）
f（9,10）= 7 + 1 * f（2,3）+ 1 * f（3,3）+ 1 * f（4,4）+ 1 * f（5,5）+ 1 * f（6 ，6）+ 1 * f（7.7）+ 1 * f（8.8）+ 1 * f（9.9）

可见一些规律性：



这些系数是从理论上计算的。 每个蓝色是顶部和左侧的总和。 紫色的与蓝色的相同，只是顺序相反。 您可以计算，但这又是递归，在其中我感到失望。 很可能，许多人（可惜不是我）已经学到了这些数字，但是现在，我将按照自己的解决方案保持这种好奇心。 我决定吐在他们身上，然后走到另一边。

他打开色板，用功能结果盖好盘子，然后开始寻找图案。 C3 = IF（C $ 2> $ B3; 2 ^ $ B3-1; C2 + B2 + 1），其中$ 2是包含鸡蛋数量的行（1-13），$ B是具有尝试次数（1-20）的列， C3-在两个蛋和一个尝试相交处的单元格。



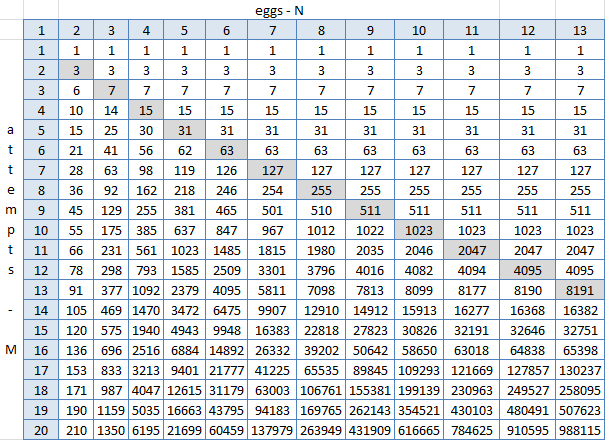
灰色对角线是N = M，在这里可以清楚地看到它的右边（对于N> M）没有任何变化。 可以看到-但是不能这样，因为这些都是公式工作的所有结果，其中给出的每个单元格等于顶部，左侧顶部和一个之和。 但是找不到一些通用的公式，您可以用它代替N和M并获得下限编号。 剧透：它不存在。 但是，那么在Excel中创建此表是如此简单，也许可以生成相同的python并从中拖动答案？

脾气暴躁你不

我记得有NumPy，它仅设计用于多维数组，为什么不尝试呢？ 首先，我们需要一个零个大小为N + 1的一维数组和一个大小为N个单位的一维数组。将第一个数组从零到倒数第二个元素，将其与第一个数组从第一个元素到最后一个元素逐个添加，并带有一个单位数组。 对于结果数组，在开头添加零。 重复M次。 结果数组的元素编号N将是答案。 前3个步骤如下所示：



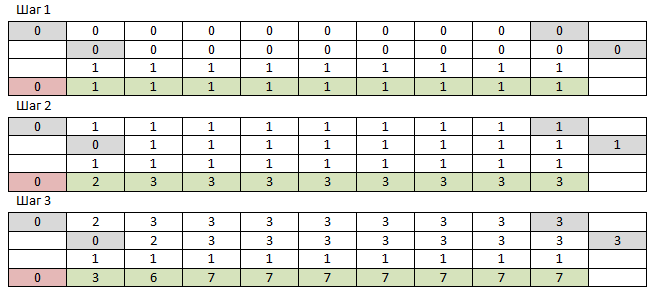
NumPy的运行速度如此之快，以至于我每次都再次读取必要的行时都没有保存整个表。 一件事-大量工作的结果是错误的。 较高的等级就像那些，而较低的等级则不是。 这就是从多个加法器中累加的浮点数的算术误差。 没关系-您可以将数组的类型更改为int。 不，麻烦-事实证明，为了提高速度，NumPy仅适用于其数据类型，并且其int与Python int不同，其值不能超过2 ^ 64-1，此后它默默地溢出并以-2 ^ 64继续。 我实际上希望数字不超过三千个字符。 但是它运行非常快，f（9477，10000）运行233毫秒，结果只是输出中有些废话。 因为这样的事情，我什至不给出代码。 我将尝试使它成为一个干净的python。

迭代，迭代但不迭代

 def height(n, m): arr = [0]*(n+1) while m > 0: arr = [0] + list(map(lambda x,y: x+y+1, arr[:-1], arr[1:])) m-=1 return arr[n] 

44秒计算f（9477，10000）有点多。 但绝对可以肯定。 有什么可以优化的？ 首先，无需考虑对角线M，M右边的所有内容。 第二个-为一个单元考虑最后一个数组的整体。 为此，前一个的后两个单元格将适合。 要计算f（10，20），仅这些灰色单元格就足够了：



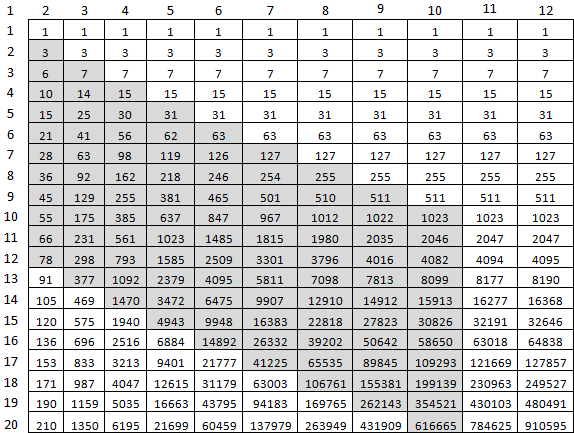
因此，它看起来在代码中：

 def height(n, m): arr = [0, 1, 1] i = 1 while i < n and i < mn: #    m,m arr = [0] + list(map(lambda x,y: x+y+1, arr[:-1], arr[1:])) arr += [arr[-1]] i+=1 arr.pop(-1) while i < n or i < mn: #        arr = list(map(lambda x,y: x+y+1, arr[:-1], arr[1:])) arr = arr + [arr[-1]+1] if n > len(arr) else [0] + arr i+=1 while i < m: # ,     -  arr = list(map(lambda x,y: x+y+1, arr[:-1], arr[1:])) i+=1 return arr[0] 

你觉得呢？ f（9477，10000）在2秒内！ 但是此输入太好了，任何阶段的数组长度都不会超过533个元素（10000-9477）。 让我们检查f（5477，10000）-11秒。 效果也不错，但仅与44秒相比-这次不会进行20次测试。

不是那样的 但是，既然有任务，那么就有解决方案，搜索将继续。 我开始再次查看Excel表。 （m，m）左边的像元总是少一个。 而且左侧的单元格不再存在，每行中的差异变得更大。 （m，m）以下的像元总是两倍大。 并且它下面的像元不再是两次，而是略小一些，但是对于每列而言，距离越远，则越大。 而且，第一行中的数字开始时快速增长，而在中间时则缓慢增长。 让我建立一个相邻单元之间的差异表，也许在那里会出现什么模式？

保暖

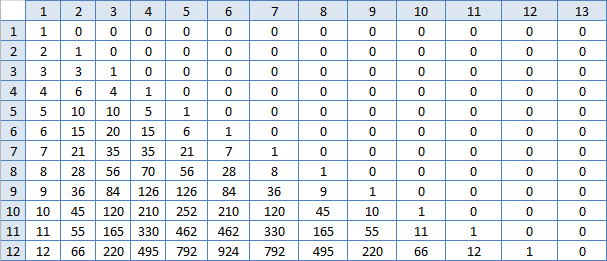
ah，熟悉的数字！ 即，行号M中这些数字的总和N是答案吗？ 没错，对它们进行计数与我已经做过的差不多，这不太可能大大加快工作速度。 但是您必须尝试：



更不用说一个更优化的解决方案。 它在某些数据上运行更快，而在某些数据上运行慢。 我们必须更深入。 这个三角形出现在溶液中两次的三角形是什么？ 承认是可耻的，但是我已经安全地忘记了三角形一定要在其中出现的高等数学，所以我不得不用谷歌搜索它。

宾果！

Pascal的Triangle ，被正式称为。 无限二项式系数表。 因此，用N个鸡蛋和M个投掷来解决问题的答案是M次的牛顿二项式展开式中前N个系数的总和，除了零。

可以通过行号和行中系数号的阶乘计算任意二项式系数：bk = m！/（N！*（Mn！））。 但是最好的部分是，您可以按顺序计算字符串中的数字，知道它的数字和零系数（总是一个）：bk [n] = bk [n-1] *（m-n + 1）/ n。 在每个步骤中，分子减少1，而分母增加。 简洁的最终解决方案如下所示：

 def height(n, m): h, bk = 0, 1 #      for i in range(1, n + 1): bk = bk * m // ih += bk m-=1 return h 

33毫秒 来计算f（9477，10000）！ 尽管在给定范围内，此解决方案也可以优化，并且效果很好。 如果n位于三角形的后半部分，则我们可以将其反转为mn，计算前n个系数的总和，然后将其从2 ^ m-2中减去。 如果n靠近中间且m为奇数，则也可以减少计算：该行的前一半的总和为2 ^（m-1）-1，可以通过阶乘计算前一半的最后一个系数，其数量为（m-1）/ 2，然后如果n在三角形的右半部分中继续相加系数，或者在n的左边中相减。 如果m为偶数，则您甚至无法计算线的一半，但可以通过阶乘计算平均值并将一半加到2 ^（m-1）-1中，从而找到前m / 2 + 1个系数的总和。 在10 ^ 6范围内的输入数据上，这非常明显地减少了执行时间。

一个成功的决定之后，我开始寻找别人对这个问题的研究，但是从访谈中我发现只有两个鸡蛋，是同一件事，这不是运动。 我决定，如果没有我的决定，互联网将是不完整的。