朱莉娅 熟人

朱莉娅颂

用这种语言来传达伴随着启动第一个程序和纠正第一个错误的所有热情是非常困难的。 像Python一样简单漂亮，有点像Fortran ，可以方便地使用数组和图形，甚至可以对虚拟对象进行剧烈的优化和并行化，例如 我 我的同学们。 您可以在不同的抽象级别上进行工作：从具有动态类型的高级编程开始，您可以使用汇编程序命令，也就是说，这里既具有Python可访问性，又具有Fortran计数器的执行速度。 我无法摆脱Mathcad ， Scilab甚至上帝原谅我的感觉， C ++开始逐渐淡出我的心。

我偶然涉足Khabrovian出版物 ，从而了解了这种语言，并且，作为一个印象深刻的学生，我开始寻求指导，最好是俄语。 自从六年来语言不断发展以来，本来就稀缺的信息源就变得过时了，令人兴奋的事情开始减少。 但是随着新的实验课程的开始，即可以自由选择编程语言来对物理现象进行建模，因此仍然有动机开始与Julia结识。 此外，八月份，该语言为“ add 1.0” 。

下面介绍的材料计划作为对编写所有实验论文和收集培训手册的语言的介绍。

Julia是用于数学计算的高级，高性能动态键入编程语言。 语法类似于matlab系列，该语言用C ， C ++和Scheme编写，可以调用Sysh库

安装方式

好了，一切终于解决了，现在由我们处理：

• JuliaPRO命令提示符 -直接从口译员那里获得所有Yulina技能。
• Juno是一个漂亮的IDE，具有用于图形显示的窗口和一个工作区，您可以在其中查看所有对象的内容
• Jupyter-在控制台中启动计算核心，您可以直接在浏览器中执行代码。 （除了朱莉娅，Python也存在）

让我们看看这个计算器可以做什么。Unicode支持-您可以使用西里尔字母，象形文字并将pi称为希腊字母。 而且，您不能显式指定数字和变量之间的乘法（以该顺序且没有空格）：

x = 5+8 2x - 3x + 2x^2 Out: 325 

所有必要的符号也都在适当的位置：+ =，* =，>> =等。 （符号“ >>”（向右移位）。比较符号：>，> =，<，<=，== 、! =。不等式可以组合成链：

 y = 5 y += 2 4 <= y < 8 Out: true 

可用的复数：

 (2-1im)*(4+3im) Out: 11 + 2im 

和与他们一起工作的功能：

• 实数（z）是实数部分，
• imag（z）是虚部，
• conj（z）是复共轭，
• abs（z） -模块，
• abs2（z）是模块的平方，
• 角度（z）是复数的参数。

您可以使用“ //”和相应的函数来使用有理数：

• num（x） -分子
• den（x） -分母，
• 浮点（x） -转换为十进制

 x = 4//6+5//7 Out: 29//21 float(x) Out: 1.380952380952381 

Julia具有控制数据内部表示的能力：

• typeof（obj） -对象的类型
• typemax（obj）是此类型的最大数量
• typemin（obj） -最小值
• eps（） -零机
• BigInt是一个大整体
• BigFloat-大浮点

 q = 3 typemax(q) Out: 9223372036854775807 typeof(q) Out: Int64 BigFloat(2.3^45/6) Out: 3.159376405019356000000000000000000000000000000000000000000000000000000000000e+15 

功能介绍

功能套件

• abs（x）是数字的模数，
• abs2（x）是模块的平方，
• sqrt（x）是平方根，
• cbrt（x）是立方根，
• exp（x）是数字的指数，
• log（x）是自然对数，
• log10（x） -十进制对数
• log（b，x）是x在底b处的对数。
  以及三角，双曲，艾里，贝塞尔等。

自定义功能：

 function () #  end 

该函数返回最后一个表达式的结果（Mathcad用户被打cup）。

 function cube(x) x^3 end cube(4) Out: 64 

好吧，或者我们明确指出：

 function myabs(x) if x>=0 return x else return -x end end myabs(-12) Out: 12 

可以在元组中收集返回值：

 function cubeandsquare(x) x^3,x^2 end a,b = cubeandsquare(3) print("a = $a, b = $b") Out: a = 27, b = 9 

函数可以包含元组，默认值和关键字。 如果函数名称后没有方括号，则将其视为变量，可以将其分配给另一个变量或将其作为参数传递给函数。 朱莉娅还支持编写程序的功能风格（您好Lisp）

 function mysin(t;A=1,?=1,?=0) #   -     A*sin(?*t + ?) end x1 = mysin(pi) #   = 0 x2 = mysin(pi*0.5,A = 2) #      x3 = mysin(pi*0.5,? = 0.5) #      print("x1 = $x1, x2 = $x2, x3 = $x3") Out: x1 = 1.2246467991473532e-16, x2 = 2.0, x3 = 0.7071067811865475 

数组

作为Scilab用户，我什至没有注意到替换：您可以使用以下函数指定数组：

• 数组{T}（undef，dims ...）-类型为T且维数为dims的数组
• 零（T，dims ...）-零数组
• 一个（T，昏暗...）-或单位
  索引从1开始 ，而不是$ -end，并且定义了矩阵的所有必需操作（要执行元素逐级加法或乘法运算，您需要在运算符前加一个点）。

（现在可以清楚地插入图片了，但是好吧...）

基本功能：

• det（A） -计算行列式
• A'-转置矩阵
• inv（A） -求逆矩阵
• 长度（A） -元素数量
• ndims（A） -尺寸数
• 大小（A） -尺寸的元组
• 尺寸（A，n） -给定方向的尺寸
• 复制（A） -创建数组的副本
• linspace（开始，结束，步骤）或
  linspace（开始：步骤：结束） -创建一维数组

 A = [1 2 3; 6 5 4; 7 8 9] Out: 3?3 Array{Int64,2}: 1 2 3 6 5 4 7 8 9 A[2,1] Out: 6 A[end] Out: 9 size(A) Out: (3, 3) 

您可以通过在维度上使用“：”符号指定索引范围来选择数组的各个部分。

 m1 = rand(3,2) m2 = reshape(1:2:11, 3,2) Out: 3?2 Base.ReshapedArray{Int64,2,StepRange{Int64,Int64},Tuple{}}: 1 7 3 9 5 11 m3 = [m1 m2] #   (  ) Out: 3?4 Array{Float64,2}: 0.325649 0.701038 1.0 7.0 0.513579 0.620215 3.0 9.0 0.815242 0.805307 5.0 11.0 m5 = [m1; m2] #   (  ) Out: 6?2 Array{Float64,2}: 0.325649 0.701038 0.513579 0.620215 0.815242 0.805307 1.0 7.0 3.0 9.0 5.0 11.0 m3[:, 2:4] Out: 3?3 Array{Float64,2}: 0.701038 1.0 7.0 0.620215 3.0 9.0 0.805307 5.0 11.0 

在这里，我们使用rand（）返回给定维数的随机数数组，并使用reshape（）将数组的维数更改为指定的维数。

 for a in A #   a   A end 

或

 for i in eachindex(A) #     i end 

或

 for i = 1 : size(A,n) # n -      (..    ) #     i end 

图表

要使用图形，您需要从存储库下载一个软件包以从中选择：

• Pkg.add（“图”）
• Pkg.add（“ PyPlot”）
• Pkg.add（“ Gadfly”）
• Pkg.add（“温斯顿”）

其中，最受欢迎的是Pythonic PyPlot 。 使用以下命令连接模块，例如：

 using PyPlot 

但是，让我们尝试使用Gnuplot（单独摆动）的Gaston。
由Gaston.jl团队加载

  Pkg.add("Gaston") 

正确地说：

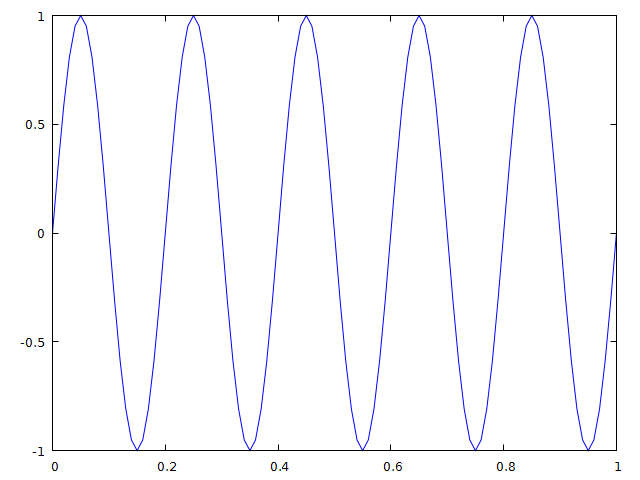
 using Gaston t = 0:0.01:1 plot(t, sin.(2?*5*t)) 

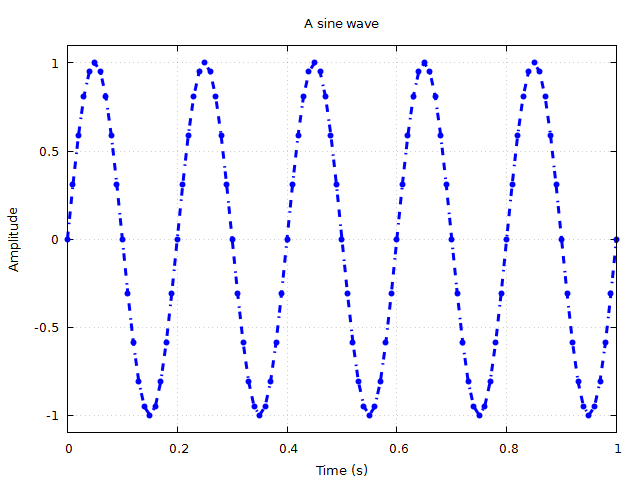
 plot(t,sin.(2?*5*t),title="A sine wave",xlabel="Time (s)",ylabel="Amplitude",grid="on",linewidth=3,color="blue", yrange="[-1.1:1.1]",marker="ecircle",plotstyle="linespoints",linestyle="-.-") 

 plot!(t,cos.(2?*5*t),color="red",linewidth=2) #       

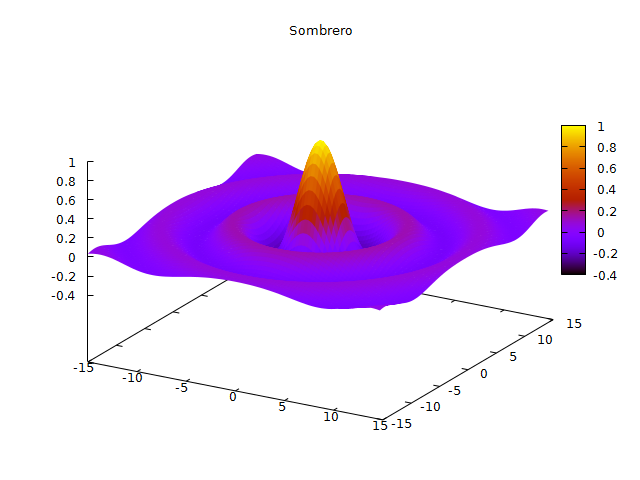
 x = y = -15:0.33:15 surf(x,y,(x,y)->sin.(sqrt.(x.*x+y.*y))./sqrt.(x.*x+y.*y),title="Sombrero",plotstyle="pm3d") 

 x = y = -15:0.33:15 surf(x,y,(x,y)->sin.(sqrt(x.*x+y.*y))./sqrt.(x.*x+y.*y), title="Edge view of a sombrero",plotstyle="pm3d",gpcom="set view 80,20") 

 R = [ x+y for x=0:5:120, y=0:5:120] G = [ x+y for x=0:5:120, y=120:-5:0] B = [ x+y for x=120:-5:0, y=0:5:120] Z = zeros(25,25,3) Z[:,:,1] = R Z[:,:,2] = G Z[:,:,3] = B imagesc(Z,title="RGB Image",clim=[10 200]) 

 histogram(rand(1000),bins=15,norm=1,title="Histogram",yrange="[0:1.6]") 

 y = 1:40 err = Gaston.ErrorCoords(rand(40)) plot(y,err=err,title="Example of error bars",plotstyle="errorbars") 

您可以使用h = Figure（）命令（仅在绘图之间插入）创建多个图形窗口（在Jupyter中不起作用）。 要将图形另存为图像文件，请使用以下命令
set_filename（“ name.png”） ＃如果未指定，将显示
printfigure（“ png”） ＃保存到文件，可用PNG，PDF，SVG和GIF
更多加斯顿包裹信息

结论

还有更多的图形软件包可以满足每种口味，几乎可以满足所有需求。 而且，辅助软件包正在与may和main一起开发。 在这里，您将拥有量子计算，生物信息学，机器学习以及诸如diffurs和导数之类的更多紧迫问题。

总的来说，朱莉娅很漂亮，聪明而且很有前途，要让她没有受到应有的照顾是绝对不允许的。