动态编程或分而治之

本文讨论解决算法问题的两种方法之间的异同： 动态编程 （动态编程）和“分而治之”的原理（分而治之）。 我们将以两种算法为例进行比较： 二进制搜索 （如何在排序数组中快速找到数字）和Levenshtein距离 （如何以最少的操作数将一行转换为另一行）。

我想马上指出，这种比较和解释并不声称是非常正确的。 甚至甚至有些大学教授也可能会开除我：)本文只是我个人的尝试，目的是梳理事物并了解什么是动态编程以及如何涉及“分而治之”的原则。

所以，让我们开始吧...

问题

当我开始研究算法时，我很难理解动态编程的基本概念（以下称为动态编程的DP ）以及它与“分而治之”方法（又称为DC ，分而治之）的区别。 在比较这两种范例时，通常许多成功使用斐波那契函数进行说明。 这是一个很好的例证。 但是在我看来，当我们使用相同的任务来说明DP和DC时，我们失去了一个重要的细节，可以帮助我们更快地了解这两种方法之间的差异。 细节在于，这两种技术最能体现出解决不同类型问题的能力。

我仍在学习DP和DC，并且不能说我完全理解这些概念。 但是我仍然希望本文能为我们提供更多的启示，并有助于下一步研究诸如动态编程和分治法之类的重要方法。

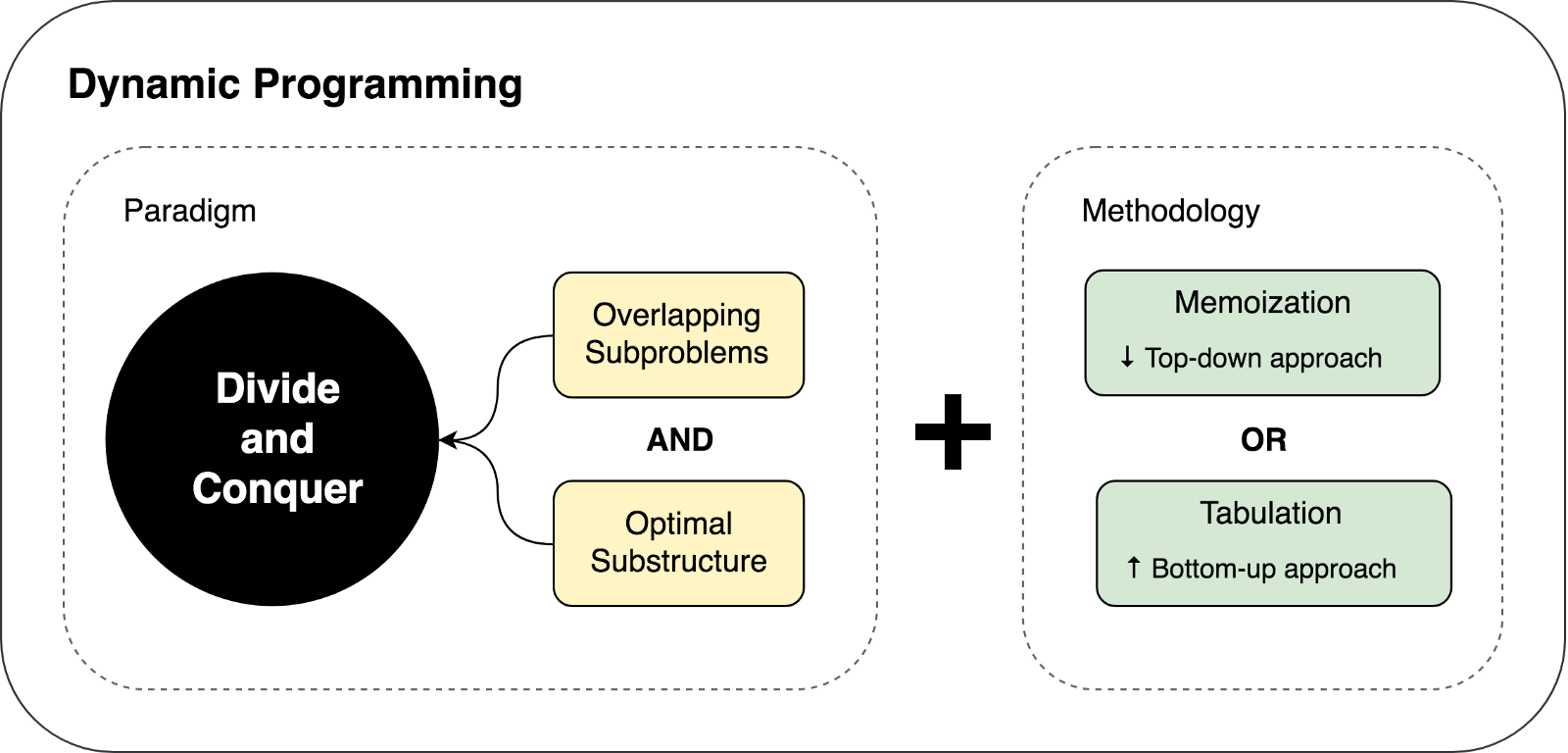
DP和DC之间的相似之处

我现在看这两个概念的方式可以断定DP是DC的扩展版本 。

我不会认为它们完全不同。 因为这两个概念都将一个问题递归地分解为两个或多个相同类型的子问题，直到这些子问题足够容易直接解决。 此外，子问题的所有解决方案都组合在一起，以便最终给出原始问题的答案。

因此，为什么我们还有两种不同的方法（DP和DC），为什么我称动态编程为扩展。 这是因为动态编程可以应用于具有某些特征和限制的任务。 并且只有在这种情况下，DP才通过两种技术扩展DC： 记忆和制表 。

让我们进一步深入细节...

动态编程所需的限制和特性

正如我们刚刚发现的那样，任务/问题必须具有两个关键特征，以便我们尝试使用动态编程来解决它：

1. 最佳子结构 -从一个最优解决方案到子任务，应该可以组成一个最优解决方案。
2. 相交的子问题 -必须将问题分解为子问题，然后再重复使用这些子问题。 换句话说，解决问题的递归方法将意味着对同一个子问题有多个（ 而不是单个）解决方案，而不是在每个递归循环中产生新的且唯一的子问题。

一旦在所考虑的问题中找到了这两个特征，就可以说可以使用动态编程来解决。

动态编程是“分而治之”原则的延伸

DP借助两种技术（ 记忆化和制表法 ）扩展了DC，其目的是将解决方案保存为子问题，以备将来使用。 因此，解决方案被子问题缓存，这导致算法性能的显着提高。 例如，斐波那契函数的“朴素”递归实现的时间复杂度为O(2 n ) 。 同时，仅在(n)执行基于动态编程的解决方案。

记忆化（从上到下填充缓存）是一种缓存技术，它将新计算的解决方案用于子任务。 使用记忆技术的斐波那契函数如下所示：

 memFib(n) { if (mem[n] is undefined) if (n < 2) result = n else result = memFib(n-2) + memFib(n-1) mem[n] = result return mem[n] } 

制表（从下至上填充缓存）是一种类似的技术，但主要侧重于填充缓存，而不是寻找子问题的解决方案。 这种情况下，需要缓存的值的计算最容易以迭代方式而不是递归地进行。 使用制表技术的斐波那契函数如下所示：

 tabFib(n) { mem[0] = 0 mem[1] = 1 for i = 2...n mem[i] = mem[i-2] + mem[i-1] return mem[n] } 

您可以在此处阅读更多有关记忆和制表比较的信息 。

这些示例中需要抓住的主要思想是，由于我们的DC问题具有重叠的子问题，因此我们可以使用以下两种缓存技术之一将解决方案的缓存用于子问题：记忆和制表。

那么DP和DC到底有什么区别

我们了解了使用动态编程的局限性和先决条件，以及DP方法中使用的缓存技术。 让我们尝试在下图中总结并描述上述想法：



让我们尝试使用DP和DC解决两个问题，以演示这两种方法的实际应用。

分而治之示例：二进制搜索

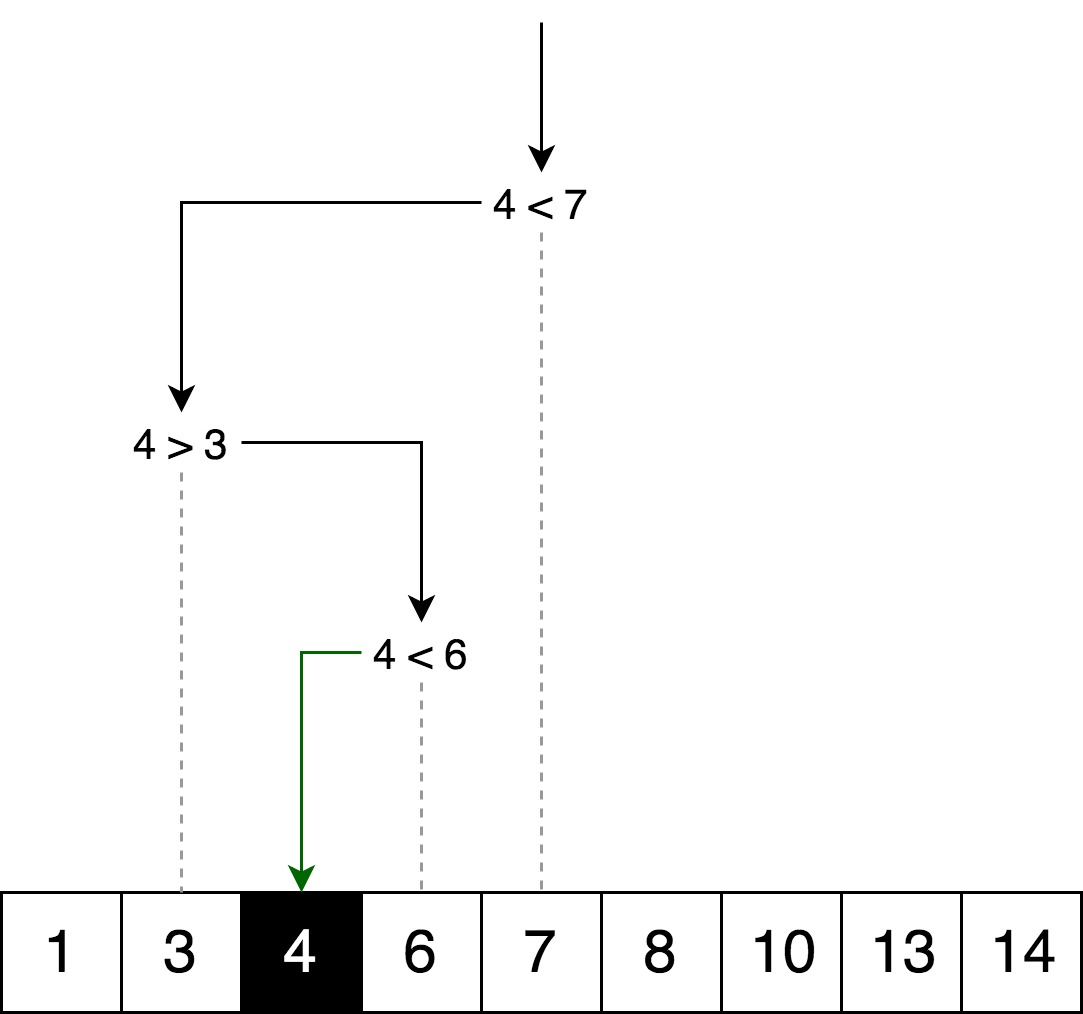
二进制搜索算法是一种搜索算法，用于查找所请求元素在排序数组中的位置。 在二进制搜索中，我们将变量的值与数组中间的元素的值进行比较。 如果它们不相等，则无法从其中排除所需元素的数组的一半继续搜索。 搜索继续在数组的那一半中进行，直到可以找到所需变量为止。 如果数组的下半部分不包含元素，则认为搜索已完成，因此我们得出结论，数组不包含所需的值。

例子

下图是对数组中数字4进行二进制搜索的示例。



让我们描绘相同的搜索逻辑，但是以“决策树”的形式。



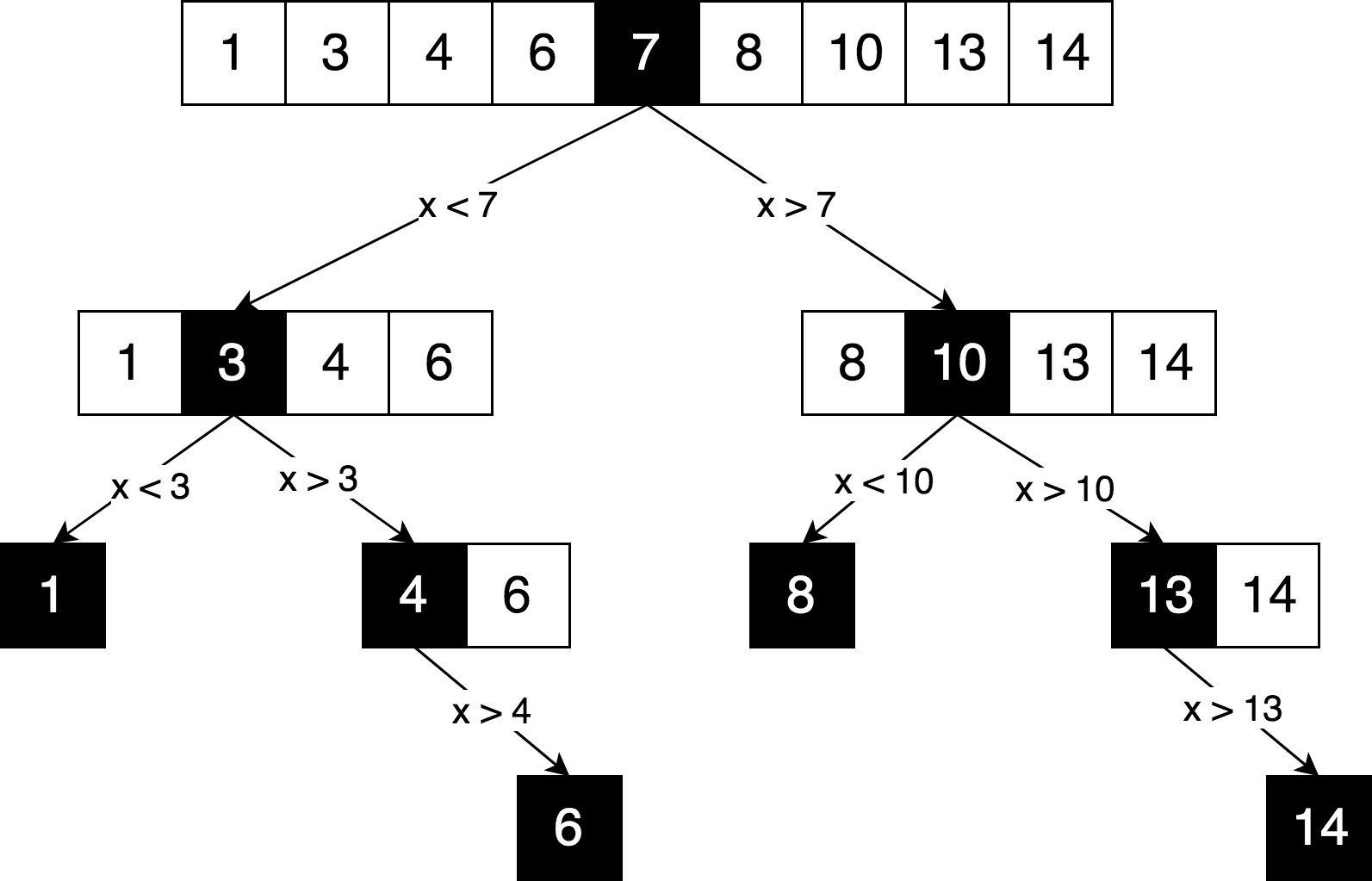
您可以在该图中看到用于解决此问题的明确原则“分而治之”。 我们迭代地将原始数组拆分为子数组，并尝试找到我们正在其中寻找的元素。

我们可以使用动态编程解决这个问题吗？ 不行 由于此任务不包含相交的子问题 。 每次我们将数组拆分为多个部分时，两个部分都是完全独立的并且不重叠。 并且根据我们上面讨论的动态编程的假设和局限性，子问题必须以某种方式重叠，它们必须是重复的 。

通常，只要决策树看起来完全像树 （而不是图 ），这很可能意味着没有重叠的子问题，

算法实现

在这里，您可以找到带有测试和解释的二进制搜索算法的完整源代码。

 function binarySearch(sortedArray, seekElement) { let startIndex = 0; let endIndex = sortedArray.length - 1; while (startIndex <= endIndex) { const middleIndex = startIndex + Math.floor((endIndex - startIndex) / 2); // If we've found the element just return its position. if (sortedArray[middleIndex] === seekElement)) { return middleIndex; } // Decide which half to choose: left or right one. if (sortedArray[middleIndex] < seekElement)) { // Go to the right half of the array. startIndex = middleIndex + 1; } else { // Go to the left half of the array. endIndex = middleIndex - 1; } } return -1; } 

动态编程示例：编辑距离

通常，在解释动态编程时， 以斐波那契函数为例。 但是在我们的例子中，让我们举一个稍微复杂的例子。 例子越多，就越容易理解这个概念。

两行之间的编辑距离 （或Levenshtein距离）是插入一个字符，删除一个字符并将一个字符替换为另一个字符（将一行变成另一行所必需）的最小操作数。

例子

例如，单词“ kitten”和“ sitting”之间的编辑距离为3，因为您需要执行三项编辑操作（两次替换和一个插入）才能将一行转换为另一行。 而且不可能找到操作更少的更快的转换选项：

1. 小猫→坐姿（用“ s”代替“ k”）
2. sitten→sittin（将“ e”替换为“ i”）
3. 坐姿→坐姿（完全插入“ g”）。

算法应用

该算法具有广泛的应用，例如，拼写检查，光学识别校正系统，不准确的字符串搜索等。

问题的数学定义

在数学上，两条直线a, b （分别为长度| a |和|b| ）之间的Levenstein距离由function lev(|a|, |b|) ，其中：



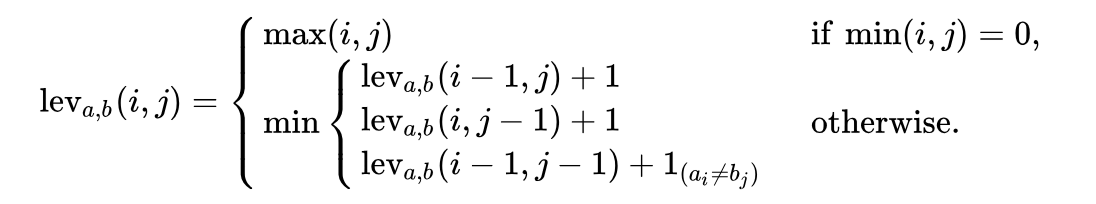
请注意， min函数中的第一行对应于删除操作，第二行对应于插入操作，第三行对应于替换操作（如果字母不相等）。

解说

让我们尝试弄清楚这个公式告诉我们什么。 举一个简单的例子，找出ME和MY行之间的最小编辑距离。 直观地，您已经知道最小编辑距离是一（ 1 ）个替换操作（将“ E”替换为“ Y”）。 但是，让我们形式化解决方案并将其转换为算法形式，以便能够解决此问题的更复杂版本，例如将Saturday一词转换为Sunday 。

为了将公式应用于转换ME→MY，我们必须首先找出ME→M，M→MY和M→M之间的最小编辑距离。 接下来，我们必须选择三个距离中的最小值，并向其添加变换E→Y的一个运算（+1）。

因此，我们已经可以看到该解决方案的递归性质：最小编辑距离ME→MY是基于之前的三个可能的转换计算的。 因此，我们已经可以说这是一个分而治之的算法。

为了进一步解释该算法，让我们将两行放在一个矩阵中：



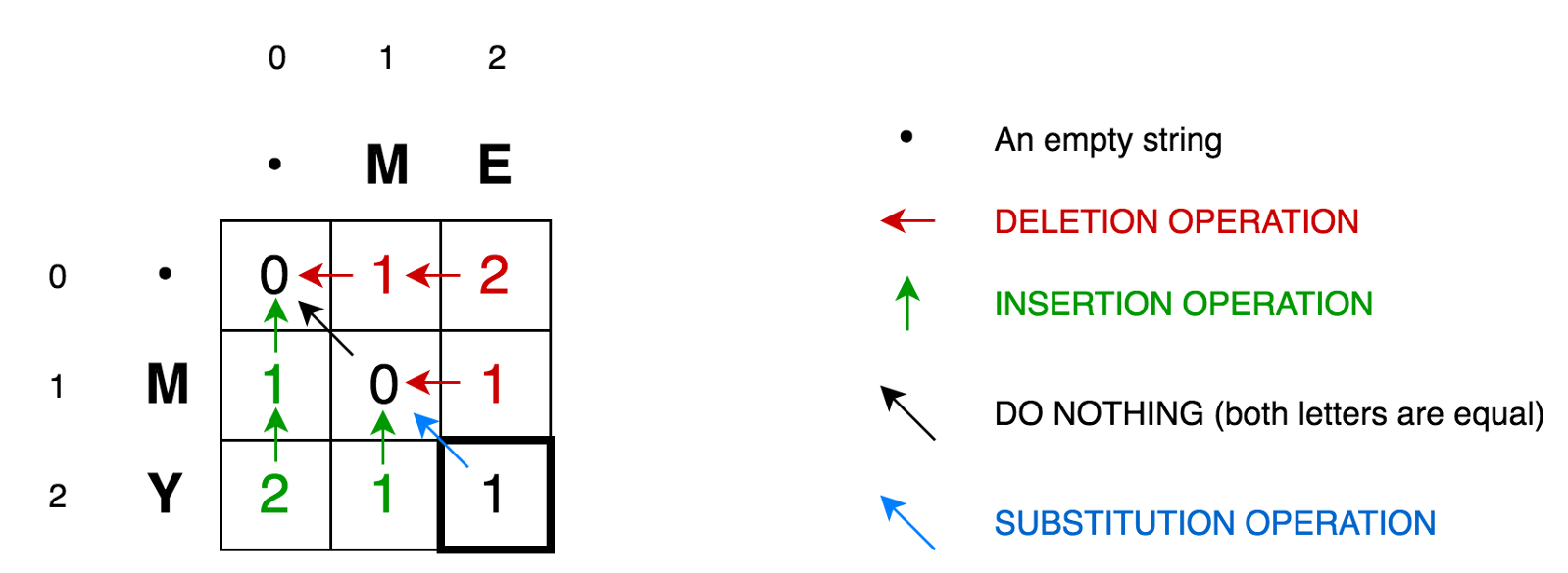单元格（0,1）包含红色数字1。这意味着我们需要执行1运算才能将M转换为空字符串-删除M。因此，我们将该数字标记为红色。

单元格（0,2）包含红色数字2。这意味着我们需要执行2次操作才能将字符串ME转换为空字符串-删除E，删除M。

单元格（1,0）包含绿色数字1。这意味着我们需要执行1个操作才能将空字符串转换为M-粘贴M。我们将插入操作标记为绿色。

单元格（2,0）包含绿色数字2。这意味着我们需要执行2次操作才能将空字符串转换为字符串MY-插入Y，插入M。

单元格（1,1）包含数字0。这意味着我们不需要执行任何操作即可将字符串M转换为M。

单元格（1,2）包含红色数字1。这意味着我们需要执行1操作才能将字符串ME转换为M-删除E。

依此类推...

对于像我们这样的小型矩阵（仅3x3）而言，看起来并不困难。 但是，如何计算大型矩阵（例如，转换为“星期六”→“星期日”中的9x7矩阵）的所有像元的值？

好消息是，根据公式，我们需要计算任何坐标为(i,j)的像元的值就是3个相邻像元(i-1,j) ， (i-1,j-1)和(i,j-1) 。 我们要做的就是找到三个相邻像元的最小值，如果在第i行和第j列中有不同的字母，则将这个值加一（+1）。

同样，您可以清楚地看到此任务的递归性质。



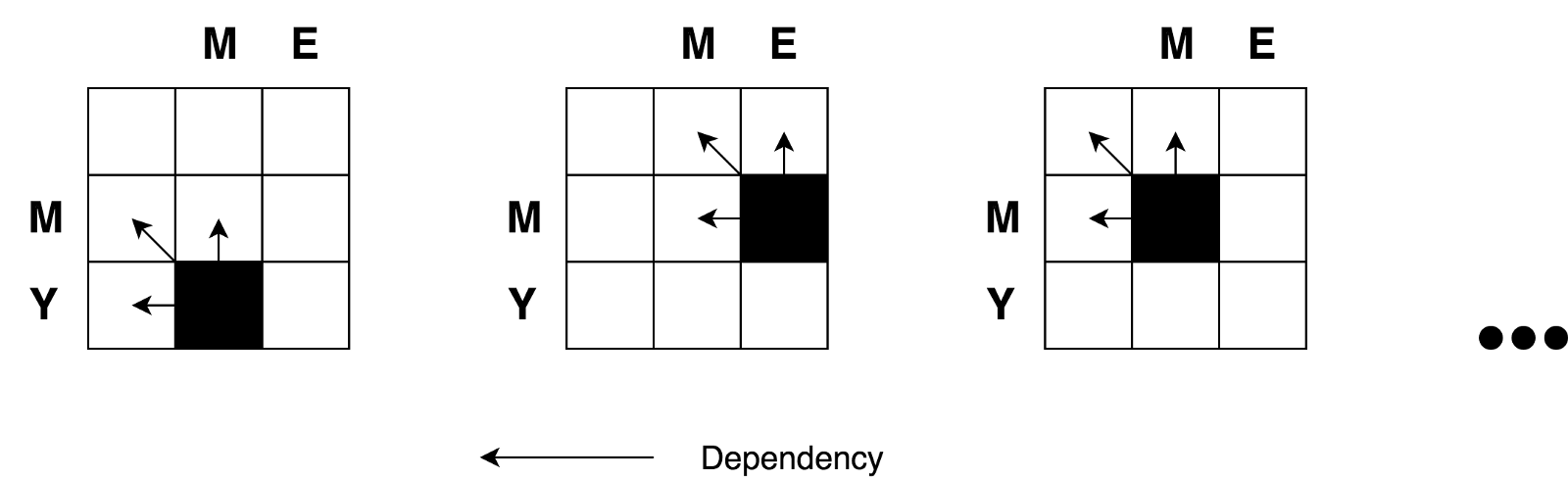
我们还看到，我们正在处理分而治之的任务。 但是，我们可以应用动态编程来解决此问题吗？ 此任务是否满足上述“ 相交问题 ”和“ 最佳子结构 ”的条件？ 是的 让我们建立一个决策树。



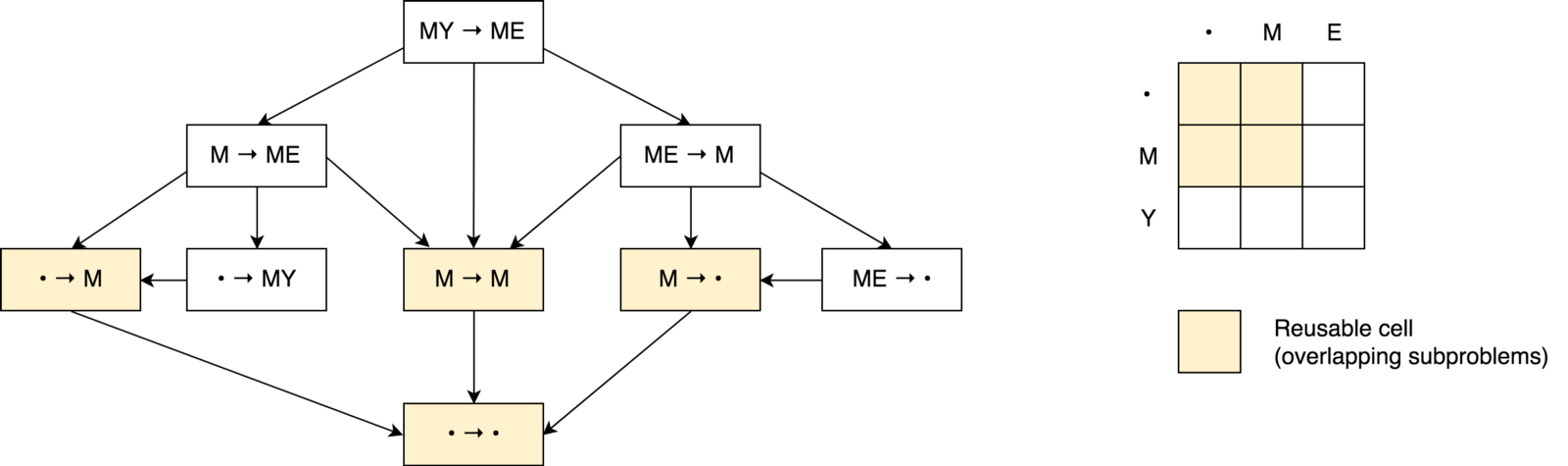
首先，您可能会注意到我们的决策树看起来更像是决策图而不是 树 。 您可能还会注意到几个重叠的子任务 。 还可以看到，不可能减少操作的数量并使之小于来自这三个相邻单元（子问题）的操作的数量。

您可能还会注意到，每个单元格中的值都是基于以前的值计算的。 因此，在这种情况下，使用制表技术（在自下而上的方向填充缓存）。 您将在下面的代码示例中看到这一点。

应用所有这些原理，我们可以解决更复杂的问题，例如，星期六→星期日的转换任务：



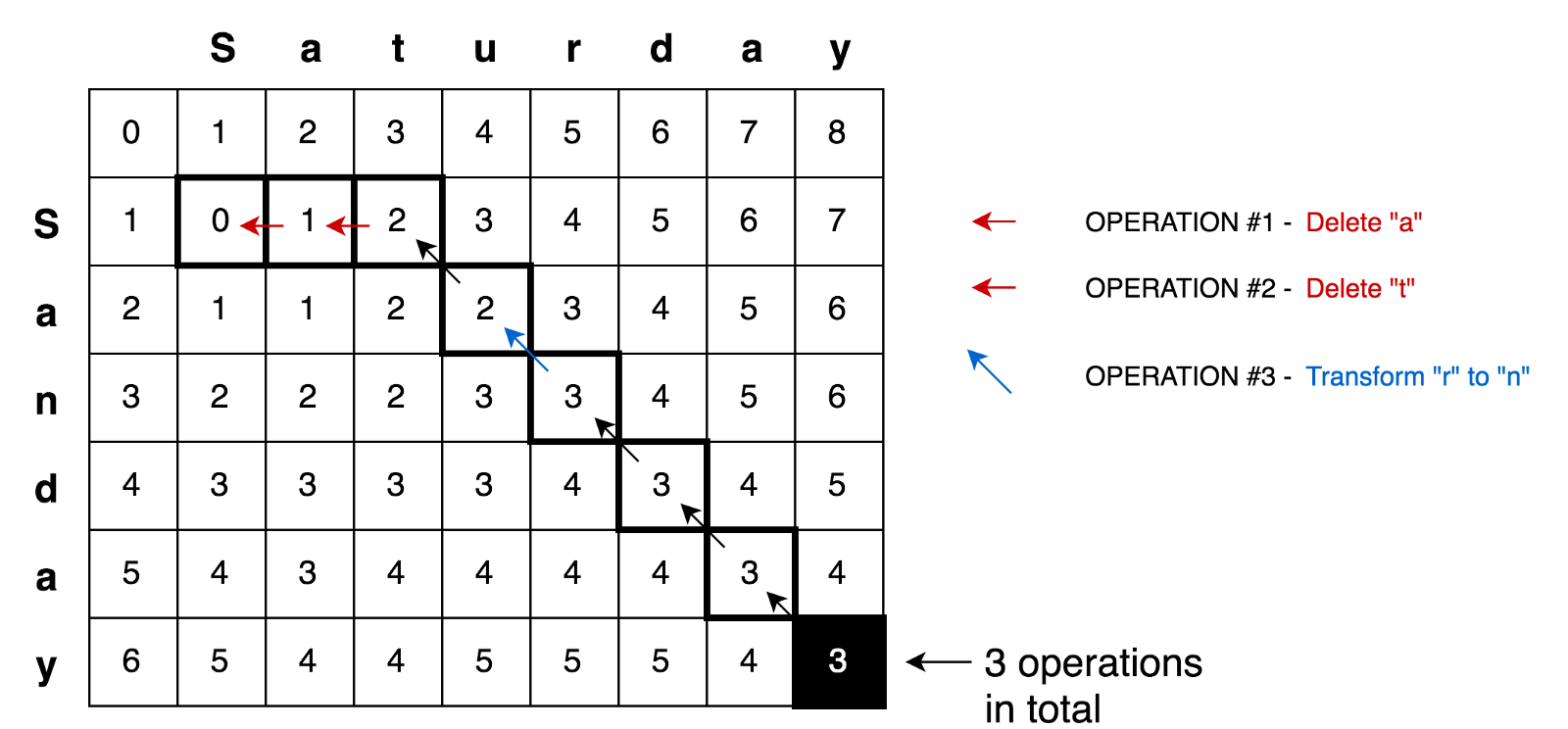代码示例

在这里，您可以找到完整的解决方案，以找到带有测试和解释的最小编辑距离：

 function levenshteinDistance(a, b) { const distanceMatrix = Array(b.length + 1) .fill(null) .map( () => Array(a.length + 1).fill(null) ); for (let i = 0; i <= a.length; i += 1) { distanceMatrix[0][i] = i; } for (let j = 0; j <= b.length; j += 1) { distanceMatrix[j][0] = j; } for (let j = 1; j <= b.length; j += 1) { for (let i = 1; i <= a.length; i += 1) { const indicator = a[i - 1] === b[j - 1] ? 0 : 1; distanceMatrix[j][i] = Math.min( distanceMatrix[j][i - 1] + 1, // deletion distanceMatrix[j - 1][i] + 1, // insertion distanceMatrix[j - 1][i - 1] + indicator, // substitution ); } } return distanceMatrix[b.length][a.length]; } 

结论

在本文中，我们比较了解决问题的两种算法方法（“动态编程”和“分而治之”）。 我们发现动态规划使用“分而治之”的原理，并且如果问题包含相交的子问题和最优子结构（如Levenshtein距离的情况），则可以应用于解决问题。 动态编程还使用记忆和制表技术来保留子分辨率，以供以后重用。

我希望本文为那些试图处理诸如动态编程和“分而治之”之类的重要概念的人们澄清而不是使情况变得复杂。

您可以在JavaScript算法和数据结构存储库中找到更多使用动态编程的算法示例，以及测试和解释。

编码成功！