“这很容易。 我们采用Schwarzschild度量，查找Christoffel符号，计算其导数，编写测地线方程，更改一些笛卡尔坐标（以免受到影响），获得大的多线ODE-并将其求解。 那样的东西。”



现在很明显，黑洞吸引了我。 他们无尽的魅力。 上次我弄清楚了如何可视化Schwarzschild几何。 我专心研究了这样一个时空的曲率如何精确影响天空外观的问题（因为来自遥远源的光子沿着黑洞弯曲的测地线移动）以创建交互式仿真。 这是结果 （在浏览器中有效）。 诀窍是最大程度地计算光线偏差。 一切都或多或少正常地工作，但是，这样的模拟当然远非理想，因为实际上没有进行任何跟踪（对于非专业人士：恢复掉落到相机中的光线的位置）。

我的新项目通过最简单的方式放弃效率/交互性来纠正此缺点： 这是纯粹在CPU上的光线跟踪器 。 跟踪尽可能准确，尽可能长地执行。 在我的笔记本电脑上，渲染以上图像花费了15 5分钟（感谢RK4）。

与同类作品相比，没有任何改善。 我真的很喜欢这样做。 我写这篇文章的目的不仅是分享结果（如上图所示）（ 特别是因为其他人做得更好 ），还包括创建这些图像的过程 ，以及对物理和实现的讨论/解释。 理想情况下，这可以激发或成为具有类似兴趣的人的指南。

在tumlr上寻找标记为starless的新鲜效果图。

一点伪黎曼光学

暗影

如果您已经尝试过我的applet ，那么您将熟悉以下图片：



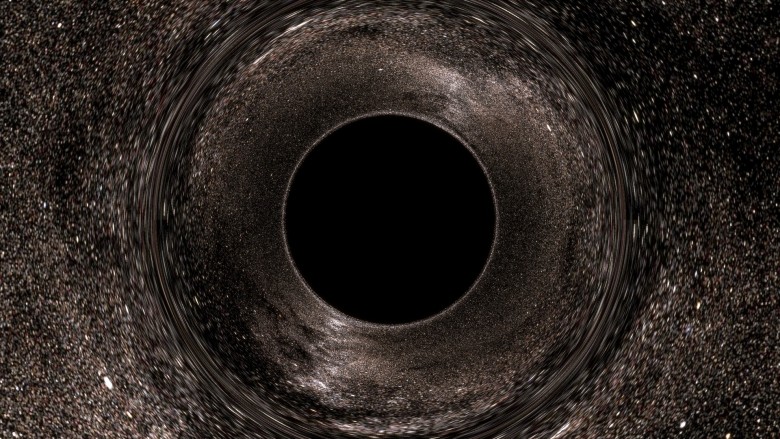
它突出了主要功能：黑盘和奇怪的失真环。

讨论经常引起注意：说黑盘是事件视界是错误的。 实际上，说图像区域是 物体是错误的。 这是一个对象的图像 。 确实，从您的眼睛到源头进行跟踪时，有些轨迹会出现在事件范围（GS）中。 这些是黑色像素，因为没有光子可以遵循从黑洞（BH）到眼睛的路径。 因此，这个黑盘非常清楚地是事件视界的图像，即如果您在遥远的过去绘制（在遥远的过去）某物，那么外部观察者将能够直接在该黑盘上看到它（我们将实际执行稍后再进行实验）。 在某些出版物中，该黑色区域也称为BH的“阴影”。



但是，有趣的是，这也是光子球 （PS）的图像 。 顶部的gnuplot图描绘了来自无限远（缩放时从远处看BH）的入射光子的测地线，以及GS（黑色）和FS（绿色）。 光子球体的半径是事件视界半径的1.5倍（在Schwarzschild几何形状中），并且此处允许黑洞周围的光子的圆形轨道（尽管不稳定）。 在图中，有些光线不存在，而另一些光线被散射（因此出现在天球的另一点）。 可以看出，对于吸收的射线，曝光参数小于〜2.5半径。 这是黑盘的视在半径，它比GS和FS 大得多 。

无论如何，以下事实很重要：

自由入射在光子球体中的光线也将到达事件视界。

这意味着光子球的图像包含在事件层的图像中。 但是由于GS显然位于FS内部，因此前者的图像也应该是后者的子集。 然后，两个图像必须匹配。

为什么我们要验证黑盘也是FS的映像？ 因为这意味着黑盘的边缘充满了沿光子球滑动的光子。 黑盘正外的像素对应于一个光子，光子（回溯时）螺旋地落入光子球体中，越来越接近不稳定的圆形轨道，旋转了很多次（看得越近，旋转速度越快），然后以螺旋状弹出-由于轨道不稳定-并逃至无限远。

此行为将引起类似于动态系统中的分体的有趣光学效果。 从理论上讲，如果光束精确地沿边缘发射，它将永远以螺旋状旋转，越来越接近光子球的圆形轨道。

对天球的影响

我们不会专注于这个主题，因为最后一个applet专用于它，它为天空中的变形提供了更好的主意（包括用于更清晰变形的UV网格选项）。

关于爱因斯坦环的几句话。 重力透镜在光学上是可区分的，因为它是与观察者直接相对的单点图像。 当来自观察者的光线平行弯曲时，以这样的视角形成环。 外部光线弯曲不充分，并保持发散； 在内部，它们弯曲得太厉害，会聚，实际上，甚至可以向后或绕一圈，如我们所见。

但是请考虑一下：如果您离黑盘足够近，光线可以绕一圈，然后平行离开。 在那里，我们应该看到爱因斯坦次级环。 实际上，可以存在任何顺序的环（任意数量的绕组）。 它们之间还应该有“奇数”环，光线平行弯曲，但指向观察者。 存在这一系列无休止的环，但是在我们的映像中（实际上，在大多数这些映像中）它是完全不可见的，因为它离磁盘边缘太近了。

事件视界失真

这幅新照片发生了一些变化。 首先，它具有更好的分辨率和背景过滤功能，以使其更具特色。 然后，我放大了BH图像（没有接近，我们距离它仍约10半径，只是一个缩放）。 但最重要的是，我在地平线上画了一个网格 。

地平线只是“一个球体”。 从技术上讲，它不是具有空间度量的标准黎曼球。 天边像光！ 这是一种以光速传播的生动说法。 但是，在Schwarzschild坐标中，它仍然是一个曲面 $$$r = 1$ 我们可以使用 $$$\ phi$ 和 $$$\ theta$ 像经度和纬度。 因此，可以以规范的方式绘制网格。 您在图像中看到她。

如果我们分析上述光子的散射/吸收曲线，则网格可以让您看到可以产生的特殊效果：

地平线的整个表面可以从任何点同时看到。

这很有趣。 当您在标准的平面时空中观察固定球体时，在任何时刻都看不到其表面的50％以内（如果接近，则由于透视而小于50％）。 但是地平线与黑盘同时可见 ：尤其要注意北极和南极。 尽管如此，尽管整个表面都放在黑盘上， 但并不能完全覆盖它 ：如果放大边缘，您会看到GE的图像一直到阴影的尽头。 您会发现一个环非常靠近外边缘，但并不位于末端。 该图像是与观察者相对的点，它定义了内部HS的“第一”图像的边界。 那么，该环与实际边缘之间是什么？ 我还没有生成放大的图片，但是还有事件地平线的另一幅完整图片 。 然后再增加一个，直到无穷大。 在阴影中压缩了整个地平线的无尽同心图像。 （非常感谢/ u / xXxDeAThANgEL99xXx指出了我错过的这种现象） 。

添加吸盘

没有吸积盘，BH的现代渲染将如何进行？ 尽管这显然是一个值得商de的问题，但诺兰的星际穿越真的可以观察到，更不用说准确性了，但是我们绝对要感谢这部轰动一时的大作，因为它流行了吸积盘的特殊变形。 在这里，我们有一个无限薄的，平坦的，水平的吸积盘从光子球延伸出来（尽管这是非常不现实的，因为轨道较低 $$$3r_S$ 不稳定，如下所述），最大半径为4，涂在白色和蓝色的笼子中。 使用这种颜色，很明显，我们面临着另一种情况，即同时可以看到对象表面的100％。

对于此图像，我将观察者移到更高的位置，以从上方稍微看一下磁盘。 您会看到磁盘两个表面的图像 ：顶部和底部。 图像在黑洞的阴影上方弯曲成弧形，因为直接在黑洞上方指向的光束会向下弯曲，以与孔后方与观察者相对的圆盘上表面会合。

这也解释了下部图像的存在：在BH下传播的光线被弯曲到BH后面的磁盘下表面。 如果仔细观察，图像会散布在整个阴影中，但是在上部，它会更细。 这对应于BH上方的光线，在孔周围形成一个几乎完整的圆圈，并撞击光盘前面的下表面。

当然，很容易得出结论，有无数的吸积盘映像在接近边缘时会很快变薄。 下一张图像已经非常薄，在边缘的下部几乎看不到。

GIF仍然有意义

在这个抽搐的动画中，我打开/关闭光偏转（以前是Schwarzschild / Minkowski）以阐明我们所讨论的一些要点。





这两个奇怪的gif是应读者的要求创建的。 首先，观察者绕黑洞以10半径的距离盘旋。 这不应被理解为实际的轨道，因为实际上在轨道上移动时没有像差。 这是一系列固定的BH图像，这些图像来自观察者在帧之间到处移动的几个点； 如果愿意的话，它是一个“绝热”轨道。

和立体声仍然相关

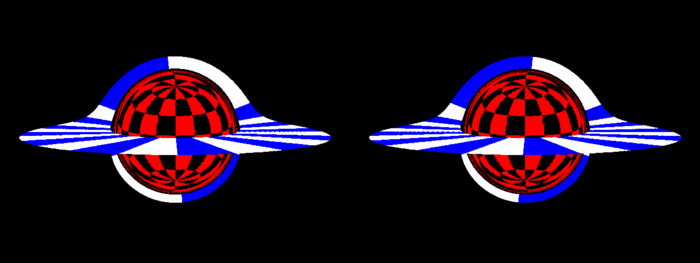
有趣的是，阴影看起来很平坦。

足够的科学

我们有足够的具有90年代风格的有毒色彩的低分辨率高分辨率照片。 这是一些“流行”效果图（单击可获得完整尺寸）。


该图像由用户/ n / dfzxh生成，具有四倍的过采样


更大的计划


戒指的放大图


从赤道平面看“光环”的邪教效应


如果下载程序，则默认为当前场景


更大的驱动力

好吧，没什么特别的。 没有图稿，只有程序的效果图。 让我们暂时回到科学上： 第三个图像似乎毫无意义，实际上非常有价值。 这是黑盘上边缘与吸积盘主映像之间的放大区域。 观察者位于吸积盘本身的外边缘，并放大图片。 目的是描绘尽可能多的不同顺序的戒指。 可以看到三个顺序：上部的较亮区域仅是磁盘上较远表面的第一张图像的下边缘。 下方的条形图在舒展的恒星的平静海面下，是圆盘下部正面图像上方的部分。 在最底部-一条细线，宽度不超过一个像素，粘贴到光子球的黑盘上。 这基本上是第三张图像：再次是较远的表面，但是在光线完成绕黑洞的附加旋转之后。 与之合并，但越来越细的图像是更高阶的环。 好吧，这也值得<blockquote>标签：

吸积盘的上表面和下表面都有无尽的图像，它们都同时显示吸盘的整个表面。 此外，除了最开始的图像外，这些图像既不在黑盘前面也不通过，也没有彼此通过，因此是“同心的”。

太好了

我接受渲染请求
对特定的可视化感兴趣，但还没有准备好克服安装程序和呈现自己的困难？ 只要给我一个reddit或邮寄给我 。 在笔记本电脑上渲染1080p所需的时间不超过10-20分钟。

现实的吸积盘

效果图中的吸积盘非常卡通化。 它只是一个愚蠢的纹理光盘。 当磁盘的外观中包含真实物理特性时，会发生什么？ 例如，当您考虑从轨道运动发生红移时会发生什么？

吸积盘的一种流行模型是几乎圆形轨道上的无限薄的物质盘。 它始于ISCO（最里面的稳定圆形轨道， $$$3r_s$ ）具有根据幂定律的温度曲线 $$$（T \ sim r ^ {-a}$ 。 我将使用一个非常简单的选项：

$$

$$T \ sim r ^ {-3/4}$$

在现实流体相对论的一般理论中，这肯定是异常的，但是在这里是这样（无论如何，您不会注意到其中的区别）。

现在，自由参数是温度的通用标度，例如ISCO中的温度。 对于大多数黑洞来说，这个温度很高。 我们正在谈论亿万开尔文； 很难想象在这样的温度下在磁盘辐射（X射线辐射的峰值）的影响下可能存在的任何人为伪影，更不用说摄影了。 因此，我们显然需要降低温度。 显然，超大质量黑洞较冷，但还不够。 我们需要将ISCO降低到10,000 K，以便至少可以看到一些东西。 这是非常不准确的，但这就是我所能做的。

应该问两个问题。 第一：在此温度下黑体是什么颜色 ？ 第二： 它有多亮 ？ 形式上，这两个问题的答案是函数的标量积，该函数用黑体谱描述了通道R，G，B。 实际上，使用了一些近似值。

对于坦纳·海兰德（Tanner Helland）的公式而言，它的颜色准确而有效，但是它包含许多光线追踪无法实现的条件（更多信息请参见下文）。 最快的方法是使用简单的纹理：



在Mitchell Charity的“黑体是什么颜色？”选择中，这种纹理是许多有用的东西之一。 。 作为参考，它对应于白点E（白点E）。

该标尺显示了从1000 K到30 000 K的温度下黑体的颜色，较高的温度对应于大约相同的蓝色阴影。 由于温度之间的亮度差异很大，因此该纹理不能也不会透射亮度。 而是将颜色归一化。 我们的任务是计算相对亮度并应用它。 分析公式适合于此。 如果我们假设可见光谱非常窄，则总可见强度与黑体本身的光谱成比例：

$$

$$\ frac {1} {\ lambda ^ 5} \ frac {1} {\ exp（\ frac {hc} {\ lambda k_B T}）-1}$$

在这里我摆脱了愚蠢的公共常数（我们仍将缩放亮度以查看某些内容）。 您只需插入 $$$\ lambda$ 大约在光谱的可见范围内，根据此公式，我们得出亮度与温度成正比：

$$

$$（e ^ {\ frac {29622.4 \ text {K}} {T}}-1）^ {-1}$$

这很简单。 作为检查，我们注意到，当T接近零时，相对强度迅速下降到零，而当T趋于无穷大时，实际上没有变化。

红移

我们在小程序的描述中讨论了Schwarzschild几何形状中的轨道速度。 要计算红移，使用来自SRT的红移公式：

$$

$$（1 + z）_ \ text {多普勒} = \ frac {1-\ beta \ cos（\ theta）} {\ sqrt {1- \ beta ^ 2}}$$

在哪里 $$$\ cos（\ theta）$ -在Schwarzschild的局部惯性坐标系中计算出的，由磁盘发射的光束方向与磁盘局部速度之间的夹角的余弦值。 由于等价原理，该公式在此情况下是正确的。

它必须乘以重力红移系数：

$$

$$（1 + z）_ \ text {引力} =（1-r ^ {-1}）^ {-1/2}$$

该系数不取决于光束的轨迹，而仅取决于辐射半径，因为Schwarzschild几何形状是固定的。

这也意味着观察者位置对引力红移的贡献在整个视场中都是恒定的。 我们的整个图像都具有恒定的总体蓝移，因为我们在BH中很深。 因此，此效果仅产生可以忽略的淡淡阴影。

我们还忽略了观察者运动的红移，因为我们的观察者在Schwarzschild几何中是静止的。 这是最终结果：



如您所见，由于色彩通道中的最大亮度，大多数光盘是完全白色的。 如果将这些通道降低到0.0-1.0的范围，则磁盘的外部部件将变浅或变黑。亮度增加太大，无法看到和欣赏。我尝试使用后处理来显示效果，以使最亮的部分显示颜色过渡，但这还不够。

令人困惑的图片。这是一幅不考虑亮度的图像，您可以在其中评估颜色：



这些图片的分辨率较低，因为它们需要很长时间才能在我的笔记本电脑上渲染（平方根不好，孩子们）。

无论如何，此渲染的壮观程度要比其他渲染少一千倍（主要是因为光盘的内边缘已经距GS足够远，所以镜头太大），但是渲染至少是准确的。如果您发现一个温度为10,000 K的黑洞并戴上好太阳镜，您会发现。

另一个特写镜头。我不自然地提高了对美的饱和度：

编写黑洞射线追踪器

Github源

黑洞的光学特性与数值积分器之间存在非常大而明显的差异，它可以产生分辨率为1080p的精美桌面墙纸。上一次我没有发布我的推理，只是提出了一个庞大而肮脏的git仓库。现在，我想详细解释一下，并尝试以更准确的形式和注释来维护代码。

我的跟踪器创建得不好，功能强大，速度很快。首先，我希望它易于设置，简化，以便人们可以获取灵感并看到改进的潜力：即使它的不完善之处也可以鼓励某人决定编写自己的版本。这是算法及其实现的简要概述。

“魔术”的潜力

因此，相对论的一般理论，一切都是清楚的。很简单 我们采用Schwarzschild度量标准，查找Christoffel符号，计算其导数，写下测地线方程，更改一些笛卡尔坐标以避免无休止的痛苦，获得巨大的多线ODE并将其求解。这样的东西。

开玩笑的 当然，有一个窍门。

如果您还记得的话，我最后一次推导以下方程式是针对Schwarzschild几何中无质量粒子在其轨道平面中的轨道（$$u = 1 / r）：$u=1/r$

$$

$$u''(\phi) + u = \frac{3}{2} u^3$$

诀窍是在这里查看Binet公式。对于中心力场的牛顿势中的牛顿粒子质量：

$$

$$\frac{d^2}{dt^2} \vec x = \frac{1}{m} F(r)$$

那么粒子显然会在其轨道平面中移动，并对应于Binet公式 $$你（ϕ ）：$u(\phi)$

$$

$$u'' + u = - \frac{1}{m h^2 u^2} F(u)$$

哪里 $$dd CP -一个素数，$\frac{d}{d\phi}$$$m是质量，并且$m$$$h是每单位质量的角动量。这是关于轨道的方程，而不是运动方程。它什么也没说$h$$$$u(t)$ 或 $$p h i （t ）仅显示了$phi(t)$$$$u$ 和 $$$\phi$ 。

让我们停下来思考一下我们实际得到的东西。该方程式表示，如果您想象一个假设的粒子在一定的中心力作用下的机械系统，则其轨迹将是Binet公式的解。然后，机械系统成为公式计算器。

那就是我在这里提供的。我们已经表明$$m = 1并采用（非物理的，无论是什么）在该特定力场中的点粒子的简单系统：$m=1$

$$

$$\vec F(r) = - \frac{3}{2} h^2 \frac{\hat r}{r^5}$$

在哪里 $$h是一个常数，对数值进行方程式求解非常简单。然后解决$h$$$→ x（T），其中$\vec x (T)$$$$T$ -实际上，该系统的抽象时间坐标是相应的Binet方程唯一的解的参数化，该Binet方程正是测地线方程 。

因此，我们在笛卡尔坐标系中求解牛顿方程，这通常是最简单的（我决定使用Runge-Kutta方法来增加步长并减少渲染时间，但将来用户将可以选择其他解决方法）。 然后，我们得到了实际的类似于光的测地线， $$$T$ 该参数是否沿用（与Schwarzschild相反） $$$t$ ，并且从正常时间开始（不存在）。

这比以前的方法要好得多，以前的方法是在轨道平面上处理极坐标。 这里的计算非常有效。

numpy中的光线跟踪

如果您查看源代码，将会看到一个Python脚本。 恐怖！ 为什么要在Python中编写光线跟踪？ 每个人都知道Python中循环运行的缓慢程度 ，这总是（几乎）结束了工作。 事实是，我们以numpy并行执行计算。 这就是为什么该程序将无法在屏幕上逐渐显示已绘制的零件的原因：它将同时渲染所有内容。

首先，我们创建一系列初始条件。 例如，一个数组(numPixel, 3)其中包含图像中所有像素的向量（numPixel-图像宽度×图像高度）。 然后，将每条射线的计算简化为(numPixel, ...)类型的数组。 由于使用numpy中的数组进行运算非常快，并且此处所有内容都是静态键入的（我希望我现在不说任何愚蠢的东西），因此应该足够快地进行计算。 也许不是C，但是仍然很快。 同时，我们拥有Python的灵活性和清晰度。

这种方法对于标准的光线跟踪来说是很糟糕的，在这种情况下，对象具有散射，反射，折射的部分，因此考虑照明条件非常重要。 例如，选择性反射一部分光线是一个真正的噩梦。 跟踪布尔值或循环索引需要多个掩码，并且循环不能中断。 但这是另一种情况：我们场景中的所有对象仅发光：天空，热吸积盘，漆黑的事件视界和明亮的灰尘。 它们不受入射光的影响，并且光本身也可以平静地通过它们，除了降低强度。 这使我们得出一种确定颜色的算法：

混色

这很容易：您只需要将我们与射线源之间的所有对象及其对应的alpha值混合在一起，然后将它们彼此放在顶部，最远的位置在底部。 我们用透明的黑色初始化颜色缓冲区，然后当与对象相交时，通过在颜色缓冲区下混合对象的颜色来更新缓冲区。 我们对灰尘执行相同的步骤（使用密度曲线 $$$r ^ {-2}$ ），并继续进行迭代。 请注意，alpha通道也可以用作Z缓冲区，因为在光线穿过不透明的对象之后，该对象将停止贡献（因此将缓冲区的alpha值设置为1.0）。

此方法的明显缺点是您无法在计算光线后停止光线跟踪，因为它是继续跟踪其他光线的数组的一部分。 例如，在与地平线碰撞后，光线落入奇点后会继续随机游荡-您可以看到如果明确关闭地平线对象会发生什么。 alpha混合算法确保它们不会影响最终图像，但是这些光线仍会加载CPU。