在火炬和张量流中均匀分布点

本文是为那些对深度学习感兴趣的人而写的，他们想要使用pytorch和tensorflow库的不同方法来最大程度地减少许多变量的功能，以及对如何将顺序执行的程序转换为使用numpy执行的矢量化矩阵计算感兴趣的人。 您还可以学习如何使用PovRay和vapory可视化的数据制作动画片。

任务来自哪里

每个都将其功能最小化（c）匿名数据科学家

在我们博客的先前出版物之一中 ，即“ Rake No. 6”段落中，我们讨论了DSSM技术，该技术可让您将文本转换为矢量。 为了找到这样的映射，人们需要找到最小化相当复杂的损失函数的线性变换系数。 由于向量的维数较大，因此很难了解学习此类模型时发生的情况。 要开发一种直觉，让您选择优化方法并设置该方法的参数，可以考虑此任务的简化版本。 现在，让向量位于我们通常的三维空间中，那么它们很容易绘制。 损失函数将具有将点推开并吸引到单位球体的潜力。 在这种情况下，解决该问题的方法是在球体上均匀分布点。 当前解决方案的质量易于通过肉眼评估。

因此，我们将寻找给定数量范围内的均匀分布 $$$n$ 点。 这种分布有时对于声学来说是必需的，以便了解向哪个方向发射晶体中的波。 Signalman-了解如何将卫星送入轨道以实现最佳质量的通信。 气象学家-用于放置气象监测站。

对于一些 $$$n$ 任务很容易解决 。 例如，如果 $$$n = 8$ ，我们可以采用立方体，并且其顶点将是问题的答案。 我们也很幸运 $$$n$ 将等于二十面体，十二面体或其他柏拉图实体的顶点数量。 否则，任务就不是那么简单。

对于足够多的点，有一个根据经验选择系数的公式， 这里 ， 这里 ， 这里和这里还有更多选择。 但是，本文致力于解决一个更通用，更复杂的解决方案 。

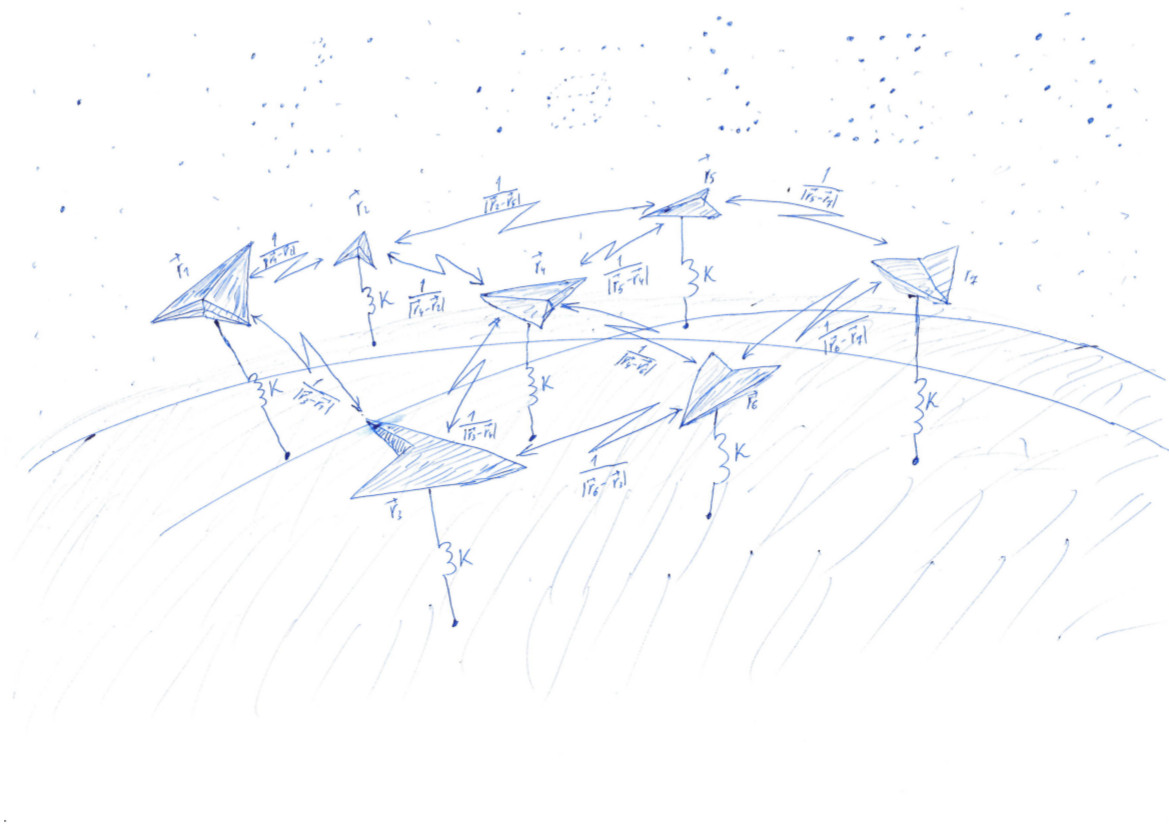
我们解决的问题与汤姆森问题 （ Wiki ）非常相似。 散布 $$$n$ 随机点，然后使它们吸引到诸如球体的表面，并相互推离。 吸引力和排斥力取决于功能-电位。 在势函数的最小值处，这些点将最均匀地位于球上。

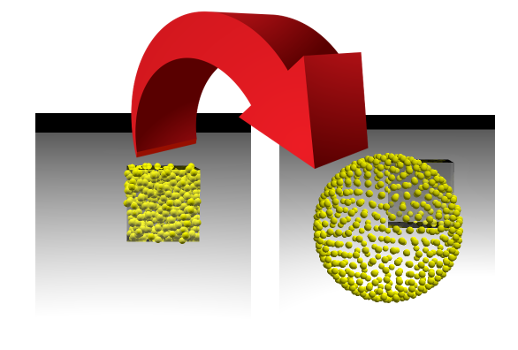
此任务与机器学习（ML）模型的学习过程非常相似，在此过程中，损失函数被最小化。 但是数据科学家通常会观察单个数字的减少情况，并且我们可以观察情况的变化。 如果成功，我们将看到随机放置在面为1的立方体内部的点如何沿着球体表面发散：

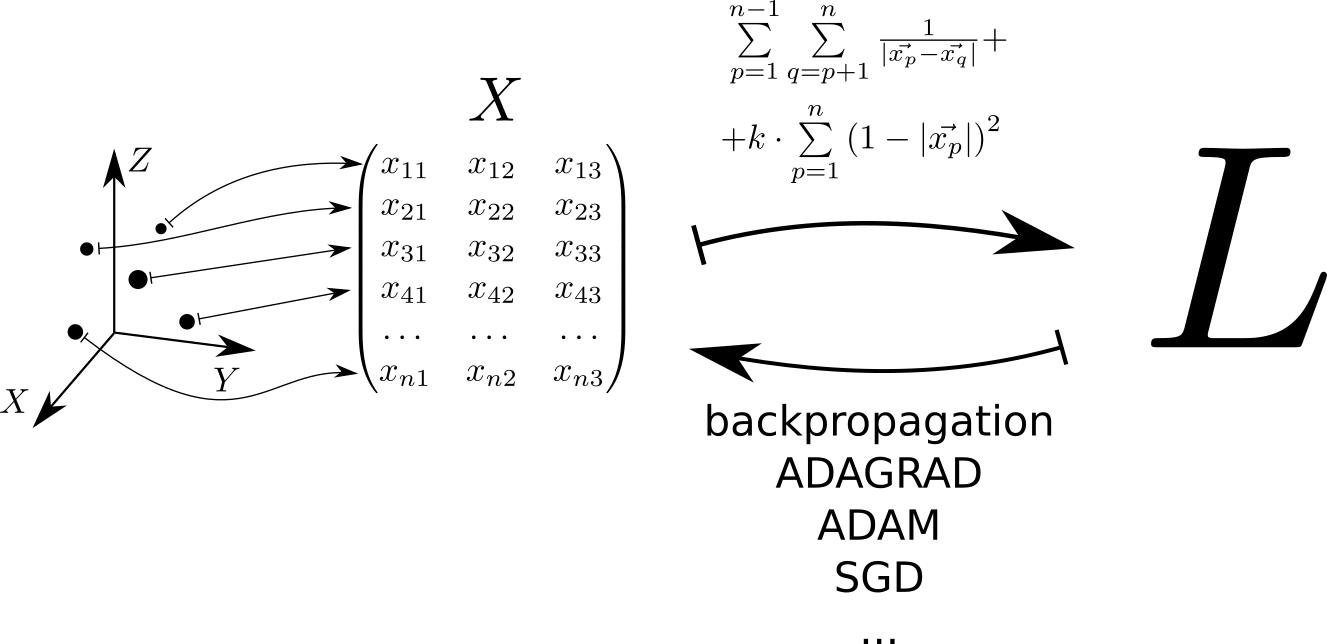
示意地，解决问题的算法可以表示如下。 位于三维空间中的每个点对应于矩阵的一行 $$$X$ 。 损失函数是从该矩阵计算出来的。 $$$L$ ，其最小值对应于球体上点的均匀分布。 可以使用pytorch和tensorflow找到最小值，从而可以通过矩阵计算损失函数的梯度 $$$X$ 并使用库中实现的一种方法降低到最低限度：SGD，ADAM，ADAGRAD等。

我们认为潜力

由于Python的简单性，表达能力和与其他语言编写的库的接口功能，Python被广泛用于解决机器学习问题。 因此，本文中的代码示例是用Python编写的。 对于快速矩阵计算，我们将使用numpy库。 为了最小化许多变量的功能-pytorch和tensorflow。

我们在面的侧面1中随机散布点。让我们有500个点，并且弹性相互作用的强度是静电的1000倍：

 import numpy as np n = 500 k = 1000 X = np.random.rand(n, 3) 

这段代码生成了一个矩阵 $$$X$ 大小 $$$3 \次n$ 填充从0到1的随机数：

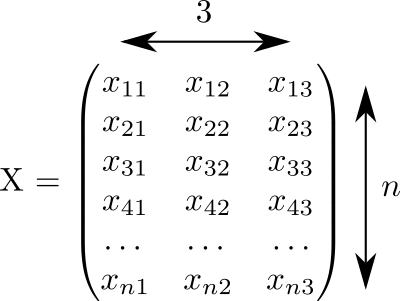
我们假设该矩阵的每一行对应一个点。 并在三列中记录坐标 $$$x，y，z$ 我们所有的观点。

点与单位球体表面的弹性相互作用的潜力 $$$u_1 = k \ cdot（1- r）^ 2/2$ 。 点的静电相互作用的潜力 $$$p$ 和 $$$q$ -- $$$u_2 = 1 / | r_p-r_q |$ 。 完整的电势包括所有成对点的静电相互作用以及每个点与球体表面的弹性相互作用：

$$

$$U（x_1，...，x_n）= \和\极限_ {p = 1} ^ {n-1} \和\极限_ {q = p + 1} ^ {n} \ frac 1 {\左| \ vec {x_p}-\ vec {x_q} \ right | } + k \ cdot \ sum \ limit _ {p = 1} ^ n \ left（1-| \ vec {x_p} | \ right）^ 2 \ rightarrow \ min$$

原则上，可以使用以下公式计算电位值：

 L_for = 0 L_for_inv = 0 L_for_sq = 0 for p in range(n): p_distance = 0 for i in range(3): p_distance += x[p, i]**2 p_distance = math.sqrt(p_distance) L_for_sq += k * (1 - p_distance)**2 #     ,     for q in range(p + 1, n): if q != p: pq_distance = 0 for i in range(3): pq_distance += (x[p, i] - x[q, i]) ** 2 pq_distance = math.sqrt(pq_distance) L_for_inv += 1 / pq_distance #      L_for = (L_for_inv + L_for_sq) / n print('loss =', L_for) 

但是有一点麻烦。 对于可悲的2000分，该程序将运行2秒钟。 如果我们使用向量化矩阵计算来计算此值，将会更快。 加速既可以通过使用“快速”语言fortran和C实现矩阵运算来实现，也可以通过使用矢量化处理器运算来实现，这些运算器允许在一个时钟周期内对大量输入数据执行操作。

让我们看一下矩阵 $$$S = X \ cdot X ^ T$ 。 它具有许多有趣的属性，并且经常在与ML中的线性分类器理论相关的计算中找到。 因此，如果我们假设在矩阵的行中 $$$X$ 带有索引 $$$p$ 和 $$$q$ 编写三维空间矢量 $$$\ vec {r _ p}，\ vec {r_q}$ 然后矩阵 $$$S$ 将由这些向量的标量积组成。 这样的载体 $$$n$ 件，然后是矩阵的尺寸 $$$S$ 等于 $$$n \倍n$ 。

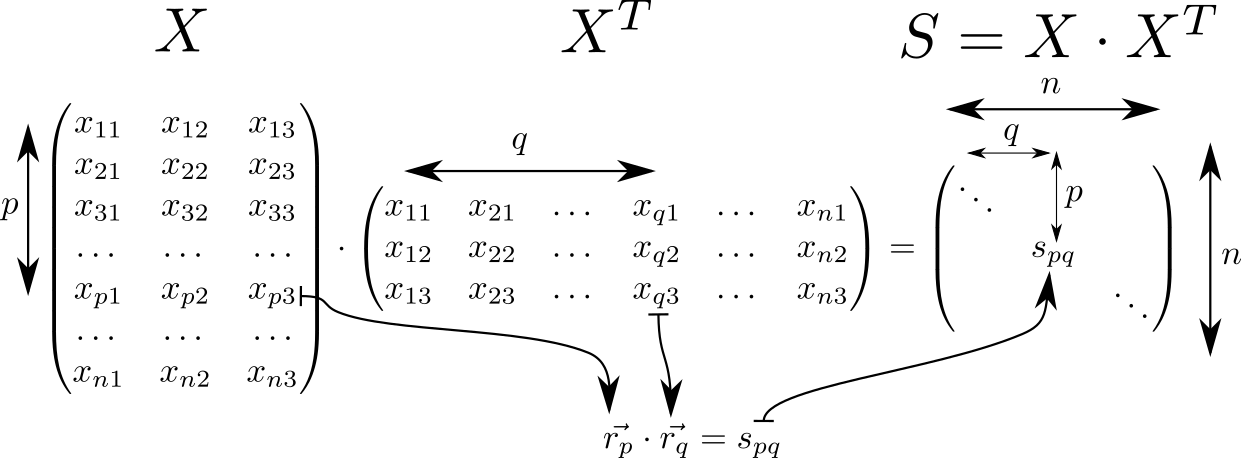
在矩阵的对角线上 $$$S$ 向量长度的平方 $$$\ vec {r_p}：s_ {p p} = r_p ^ 2$ 。 了解了这一点，让我们考虑一下交互的全部潜力。 我们首先计算两个辅助矩阵。 在一个对角矩阵中 $$$S$ 将在行中重复，在另一行-列中重复。

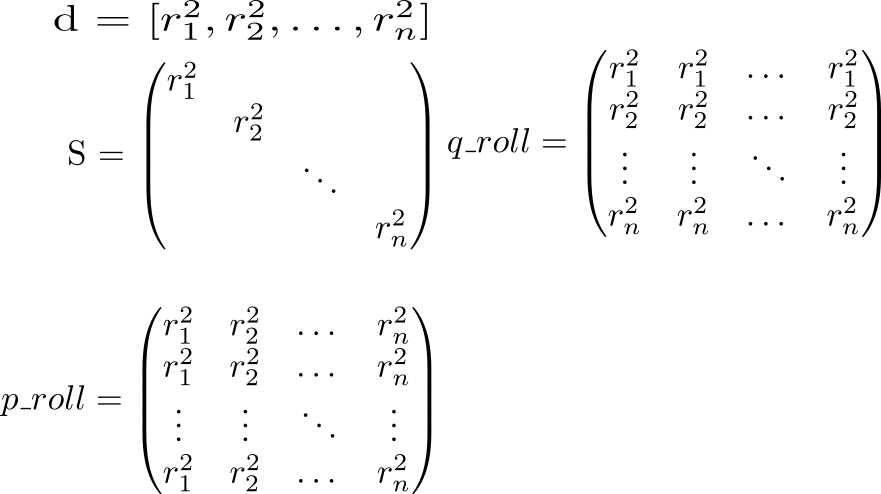
现在让我们看一下表达式p_roll + q_roll - 2 * S

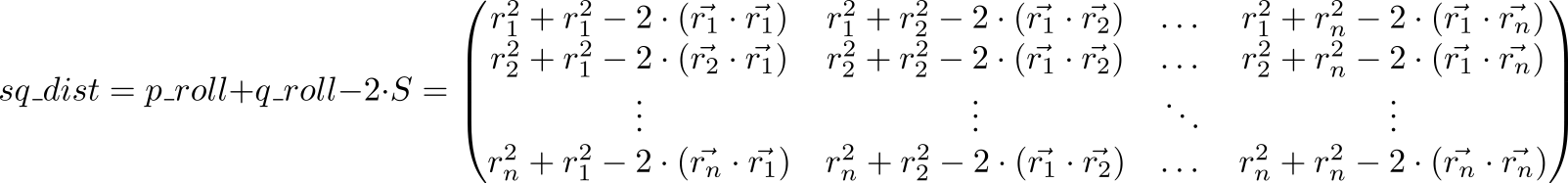
索引项目 $$$（p，q）$ 矩阵sq_dist等于 $$$r_p ^ 2 + r_q ^ 2-2 \ cdot（\ vec {r_p}，\ vec {r_q}）=（\ vec {r_p}-\ vec {r_q}）^ 2$ 。 也就是说，我们具有点之间距离的平方的矩阵。

球上的静电排斥

dist = np.sqrt(sq_dist) -点之间距离的矩阵。 我们需要考虑它们之间的点的排斥力和对球体的吸引力来计算势能。 将单位放在对角线上，并用其倒数替换每个元素（只是不要以为我们求矩阵求逆！）： rec_dist_one = 1 / (dist + np.eye(n)) 。 结果是在对角线上有一个单位的矩阵，其他元素是这些点之间的静电相互作用的电势。

现在我们将吸引的二次势加到单位球体的表面。 距球体表面的距离 $$$（1-r）$ 。 平方并乘以 $$$k$ ，它定义了粒子的静电排斥作用与球体吸引力之间的关系。 总k = 1000 ， all_interactions = rec_dist_one - torch.eye(n) + (d.sqrt() - torch.ones(n))**2 。 期待已久的损失函数，我们将其最小化： t = all_interactions.sum()

一个使用numpy库计算潜力的程序：

 S = X.dot(XT) #    pp_sq_dist = np.diag(S) #  p_roll = pp_sq_dist.reshape(1, -1).repeat(n, axis=0) #     q_roll = pp_sq_dist.reshape(-1, 1).repeat(n, axis=1) #     pq_sq_dist = p_roll + q_roll - 2 * S #      pq_dist = np.sqrt(pq_sq_dist) #    pp_dist = np.sqrt(pp_sq_dist) #      surface_dist_sq = (pp_dist - np.ones(n)) ** 2 #       rec_pq_dist = 1 / (pq_dist + np.eye(n)) - np.eye(n) #      L_np_rec = rec_pq_dist.sum() / 2 #     L_np_surf = k * surface_dist_sq.sum() #       L_np = (L_np_rec + L_np_surf) / n #   ,     print('loss =', L_np) 

这里的情况要好一些-在2000点处为200毫秒。

我们使用pytorch：

 import torch pt_x = torch.from_numpy(X) # pt_x -   tensor   pytorch pt_S = pt_x.mm(pt_x.transpose(0, 1)) # mm - matrix multiplication pt_pp_sq_dist = pt_S.diag() pt_p_roll = pt_pp_sq_dist.repeat(n, 1) pt_q_roll = pt_pp_sq_dist.reshape(-1, 1).repeat(1, n) pt_pq_sq_dist = pt_p_roll + pt_q_roll - 2 * pt_S pt_pq_dist = pt_pq_sq_dist.sqrt() pt_pp_dist = pt_pp_sq_dist.sqrt() pt_surface_dist_sq = (pt_pp_dist - torch.ones(n, dtype=torch.float64)) ** 2 pt_rec_pq_dist = 1/ (pt_pq_dist + torch.eye(n, dtype=torch.float64)) - torch.eye(n, dtype=torch.float64) L_pt = (pt_rec_pq_dist.sum() / 2 + k * pt_surface_dist_sq.sum()) / n print('loss =', float(L_pt)) 

最后张量流：

 import tensorflow as tf tf_x = tf.placeholder(name='x', dtype=tf.float64) tf_S = tf.matmul(tf_x, tf.transpose(tf_x)) tf_pp_sq_dist = tf.diag_part(tf_S) tf_p_roll = tf.tile(tf.reshape(tf_pp_sq_dist, (1, -1)), (n, 1)) tf_q_roll = tf.tile(tf.reshape(tf_pp_sq_dist, (-1, 1)), (1, n)) tf_pq_sq_dist = tf_p_roll + tf_q_roll - 2 * tf_S tf_pq_dist = tf.sqrt(tf_pq_sq_dist) tf_pp_dist = tf.sqrt(tf_pp_sq_dist) tf_surface_dist_sq = (tf_pp_dist - tf.ones(n, dtype=tf.float64)) ** 2 tf_rec_pq_dist = 1 / (tf_pq_dist + tf.eye(n, dtype=tf.float64)) - tf.eye(n, dtype=tf.float64) L_tf = (tf.reduce_sum(tf_rec_pq_dist) / 2 + k * tf.reduce_sum(tf_surface_dist_sq)) / n glob_init = tf.local_variables_initializer() #     with tf.Session() as tf_s: #     glob_init.run() #   res, = tf_s.run([L_tf], feed_dict={tf_x: x}) #   print(res) 

比较这三种方法的性能：

ñ	蟒蛇	麻木	火炬	张量流
2000	4.03	0.083	1.11	0.205
10,000	99	2.82	2.18	7.9

相对于纯python代码，矢量化计算所获得的十进制小数位数以上。 可以看到pytorch中的“样板”：小体积计算需要花费大量时间，但是随着计算量的增加，它几乎不会改变。

可视化

如今，可以使用大量的程序包（例如Matlab，Wolfram Mathematica，Maple，Matplotlib等）来可视化数据。在这些程序包中，有许多复杂的函数可以完成复杂的事情。 不幸的是，如果您面对一个简单但非标准的任务，就会发现自己没有武装。 在这种情况下，我最喜欢的解决方案是povray。 这是一个非常强大的程序，通常用于创建照片级逼真的图像，但是它可以用作“可视化的汇编程序”。 通常，无论您要显示的表面多么困难，只要让povray绘制中心位于该表面的球体即可。

使用vapory库，您可以直接在python中创建一个povray场景，对其进行渲染并查看结果。 现在看起来像这样：

图片如下：

 import vapory from PIL import Image def create_scene(moment): angle = 2 * math.pi * moment / 360 r_camera = 7 camera = vapory.Camera('location', [r_camera * math.cos(angle), 1.5, r_camera * math.sin(angle)], 'look_at', [0, 0, 0], 'angle', 30) light1 = vapory.LightSource([2, 4, -3], 'color', [1, 1, 1]) light2 = vapory.LightSource([2, 4, 3], 'color', [1, 1, 1]) plane = vapory.Plane([0, 1, 0], -1, vapory.Pigment('color', [1, 1, 1])) box = vapory.Box([0, 0, 0], [1, 1, 1], vapory.Pigment('Col_Glass_Clear'), vapory.Finish('F_Glass9'), vapory.Interior('I_Glass1')) spheres = [vapory.Sphere( [float(r[0]), float(r[1]), float(r[2])], 0.05, vapory.Texture(vapory.Pigment('color', [1, 1, 0]))) for r in x] return vapory.Scene(camera, objects=[light1, light2, plane, box] + spheres, included=['glass.inc']) for t in range(0, 360): flnm = 'out/sphere_{:03}.png'.format(t) scene = create_scene(t) scene.render(flnm, width=800, height=600, remove_temp=False) clear_output() display(Image.open(flnm)) 

使用ImageMagic从一堆文件中组装动画gif：

 convert -delay 10 -loop 0 sphere_*.png sphere_all.gif 

在github上，您可以看到工作代码，此处提供了片段。 在第二篇文章中，我将讨论如何开始使函数最小化，以便使点从立方体中出来并在球体上均匀分布。