在许多任务中,应限制输出值的范围,而输入数据不能保证这一点。 除了强迫情况外,信号限制还可以是面向目标的任务,例如,在压缩信号或实现“过载”效果时。
约束的最简单实现是在超过特定级别时将其强制为特定值。 例如,对于振幅增加的正弦曲线,它将看起来像这样:

在此,Clip函数用作限制器,作为输入信号和限制参数的传输参数,该函数的结果是输出信号。
让我们分别看一下裁剪功能图:
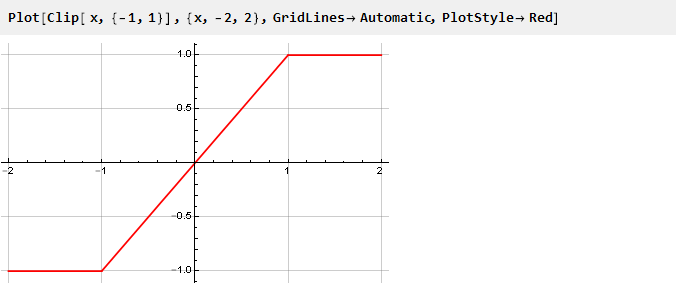
从中可以看出,虽然我们没有超过限制的极限,但输出值等于输入,信号不变。 当超过该值时,输出值无论如何都不依赖于输入,而是保持在同一水平。 实际上,我们有一个由三个其他函数组成的分段连续函数:y = -1,y = x和y = 1,它根据参数选择,并且等效于以下表示法:

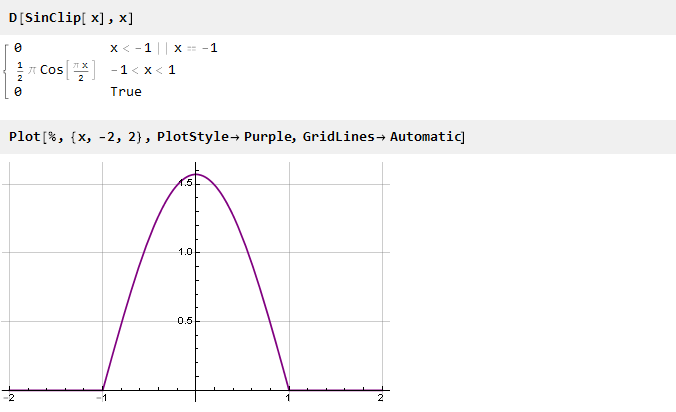
功能之间的过渡相当突然。 并且看起来很诱人,使其更流畅。 从数学上讲,这种清晰度是由于对接点上的函数导数不重合。 通过绘制Clip函数的导数可以很容易地看出这一点:
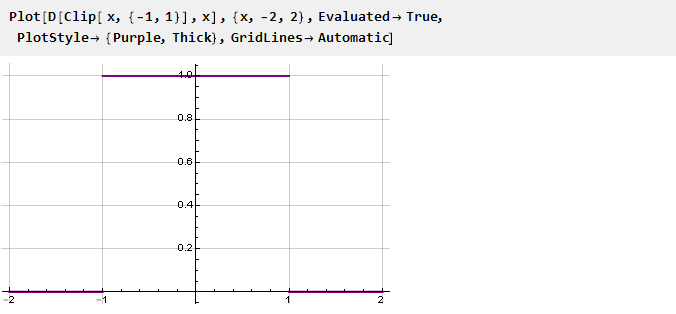
因此,为了确保约束函数的平滑性,必须确保连接点处的导数相等。 并且由于我们拥有的极限函数是常数,其导数等于零,因此在对接点处导出的限制函数也必须等于零。 接下来,我们将考虑其中的一些功能以确保平稳对接。
窦
最简单的方法是在-pi / 2到pi / 2的区间上使用sin函数,在其边界处,根据定义,导数的值等于零:
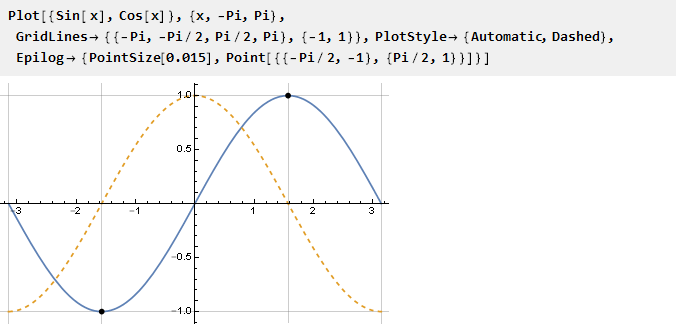
您只需要缩放参数即可将单位投影到Pi / 2上。 现在我们可以定义边界函数本身:

并制定她的时间表:
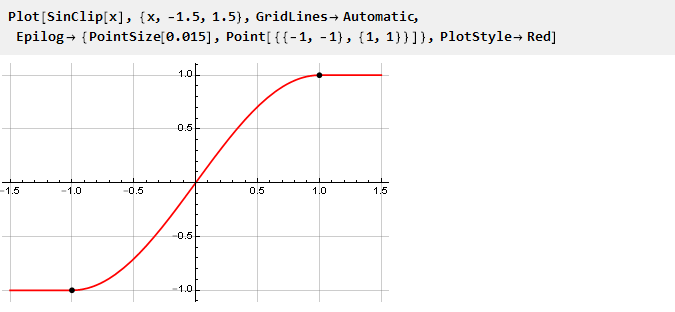
由于严格限制了我们的限制,因此可以通过缩放输入信号并随后进行反缩放来设置限制。
不再存在输入信号无失真地传输到输出的情况-增益电平越低,由于限制而导致的失真电平越低-但信号在任何情况下都会失真。
增益参数对信号失真的影响还可以从动态中看出:

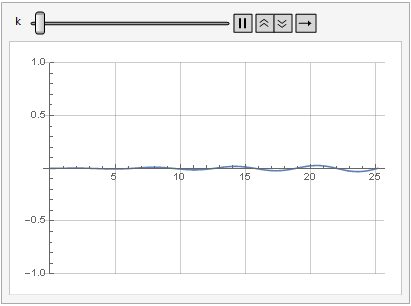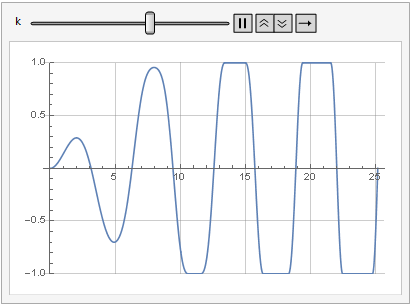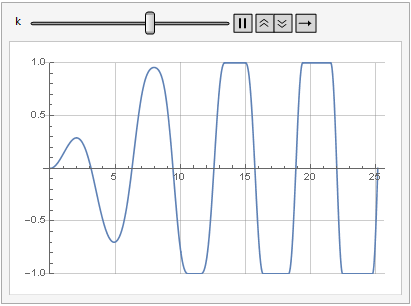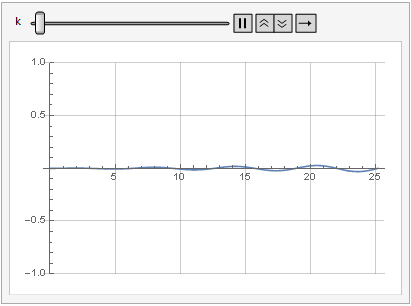
更加光滑
让我们看一下函数的派生:
它在值上不再有空隙,但在导数上有空隙(如果从原始函数算起,则为第二个)。 为了消除它,您可以采取相反的方法-首先形成平滑导数,然后对其进行积分以获得所需的功能。
使-1点和1点的导数无效的最简单方法是简单地对函数求平方-函数的所有负值都将变为正,因此,拐点将出现在函数与零的交点处。
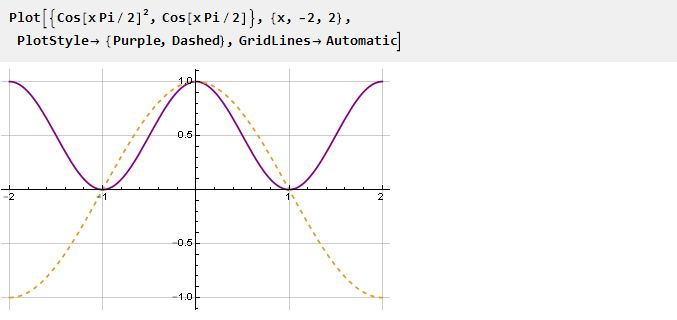
查找反导数:
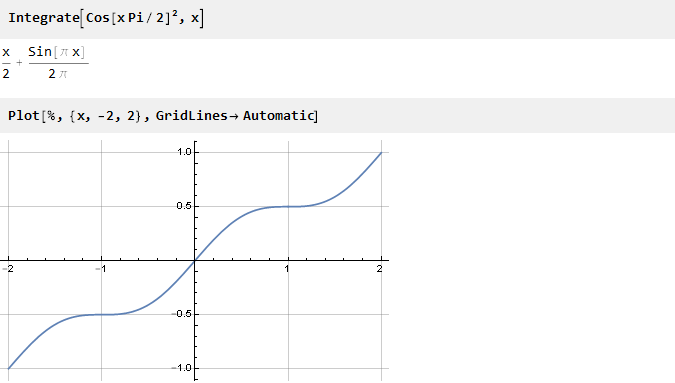
现在,它仍然可以沿纵坐标轴缩放。 为此,请在第1点找到其值:

然后除以它(是的,特别是这里是2的基本乘法,但这并不总是发生):

因此,最终限制函数将采用以下形式:
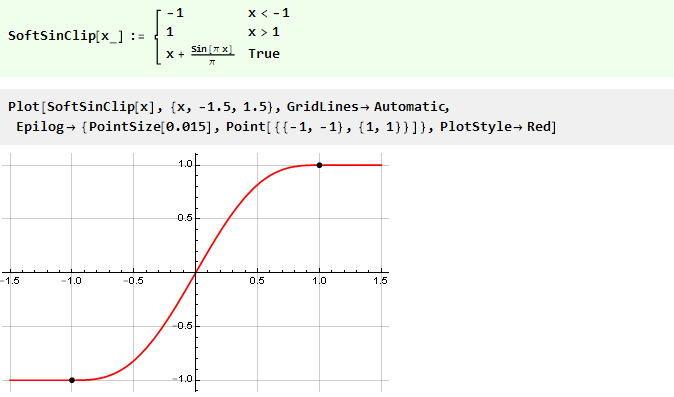
我们传递给多项式
在某些情况下,使用三角函数可能会有些浪费。 因此,我们将尝试构建所需的功能,并将其保留在基本数学运算的框架内。
考虑抛物线:
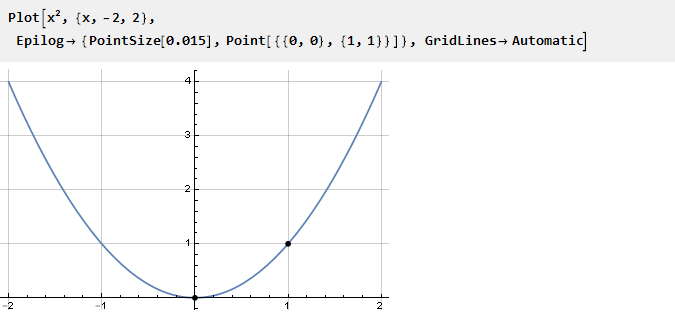
由于它已经在零点处出现了拐点,因此我们可以在区间{0,1}上使用相同的部分与常量对接。 对于负值,需要向下和向左移动:

对于正数-垂直和水平反射:

我们的抛物线函数将采用以下形式:
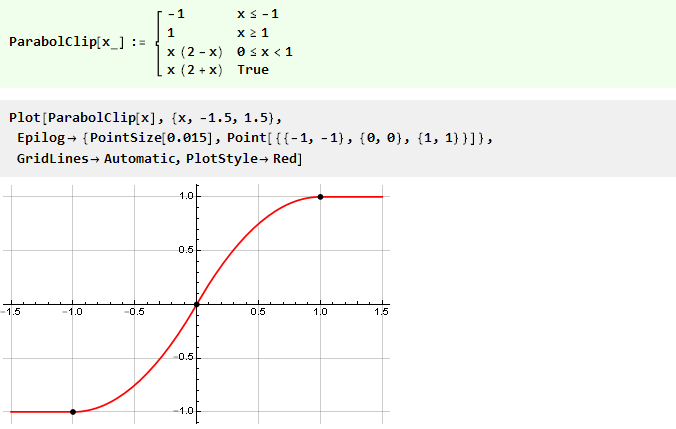
让我们复杂一点
让我们回到抛物线,将其翻转并向上移动一个单位:
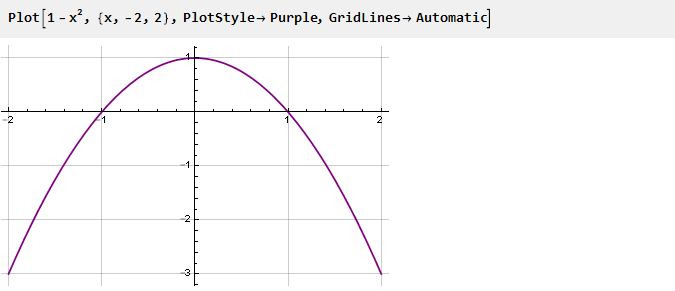
这将是我们功能的衍生。 为了使连接点更平滑,我们将进行平方运算,以这种方式将二阶导数归零:
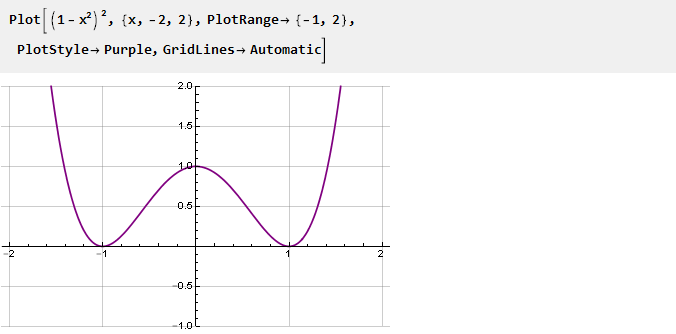
整合和扩展:

我们得到了更平滑的功能:
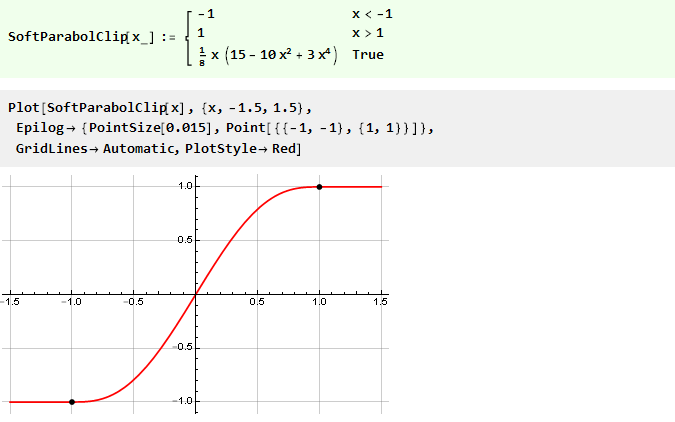
使平滑之神更加平滑
在这里,我们尝试在更高导数的对接点实现平滑。 为此,首先,我们将函数定义为系数未知的多项式,然后尝试通过方程组的解来找到系数。
让我们从一阶导数开始:

第二名:

第三名:

所有这些系数似乎都具有某种逻辑。 我们写出这些因子,然后将它们乘以x的度数; 为了避免每次都写相同的东西,我们将查找系数的过程自动化:
 它看起来像
它看起来像二项式系数。 我们大胆地假设它们是,并在此基础上编写广义公式:

检查:
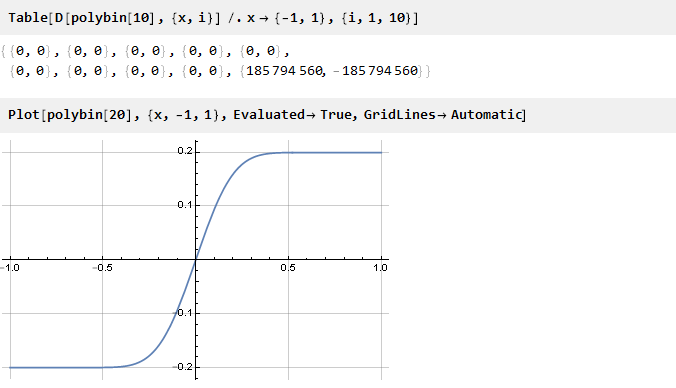
看来是真的
[1] 。 剩下的只是计算比例因子以使边缘统一:

经过缩放和简化后,我们发现我们的数学知识有些过时
[2] :
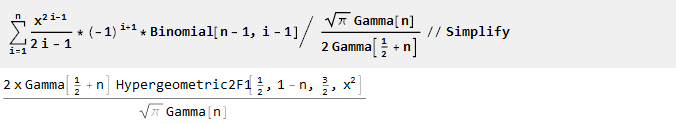
因此,我们获得了n阶的生成函数,其中n-1个一阶导数等于零:

让我们看看发生了什么:
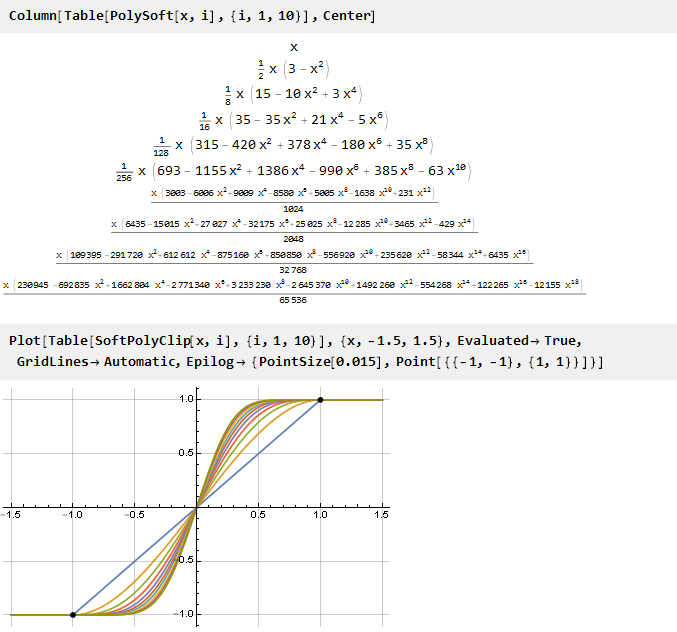
而且由于我们的广义公式证明是连续的,因此您可以根据需要使用非整数参数值:
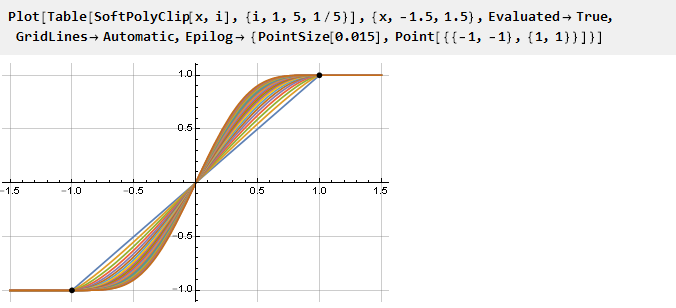
您还可以建立减少到一个比例的导数图:
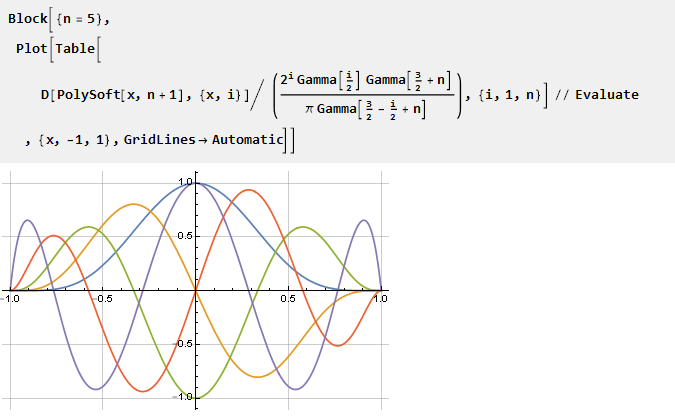
增加刚度
能够调整限制的“刚性”程度将很诱人。
让我们回到倒抛物线,并在x处添加一个系数:

n越大,我们的导数就是“平方”,其反导数就越尖锐:
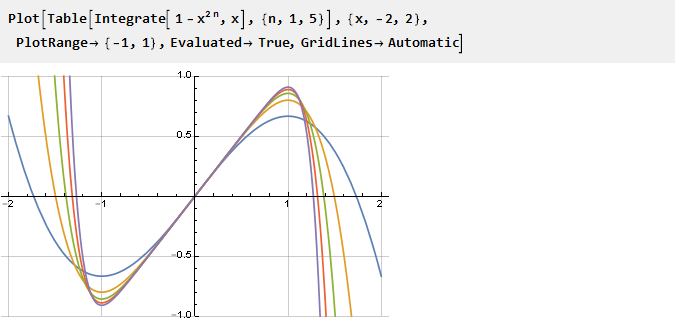
我们计算反导数并调整比例:

现在,让我们尝试设置参数的小数步:
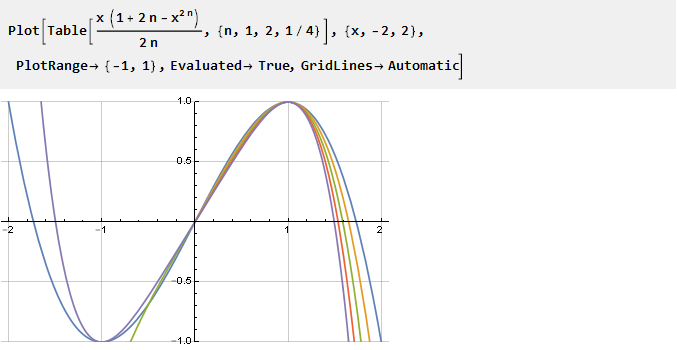
如您所见,并非所有n在负数部分都具有正确的解,但在右边(正数)部分中仍满足我们所需的条件-因此,对于负数,我们可以简单地将其与反向参数一起使用。 并且由于参数的定义域不再仅限于正整数,因此可以通过将2n替换为n来简化公式:

并将n替换为n-1,可以使公式更漂亮:
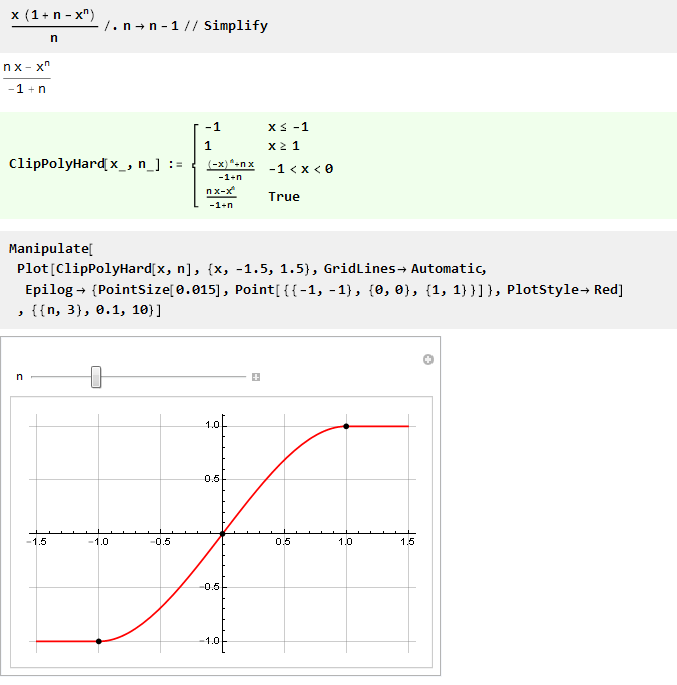
由于对于n等于1,我们得到零除,然后尝试找到极限:

找到了极限,这意味着现在我们可以将
[ n
]的函数添加到
[3]到1,并考虑所有n个大零:
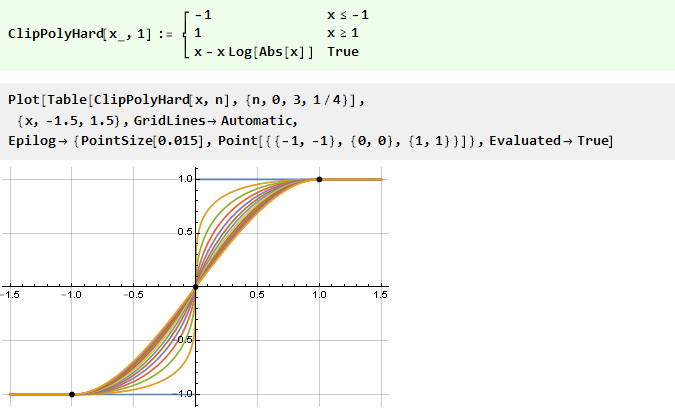
如果我们最初对倒抛物线进行平方,我们将获得更平滑的函数:
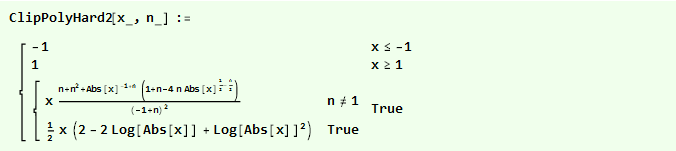
我们可以在一张图表上进行比较:
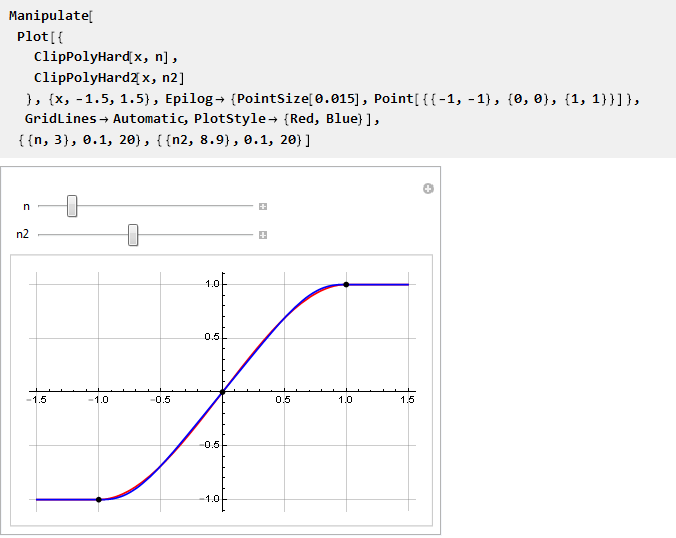
简化它
让我们看一下下面的函数:
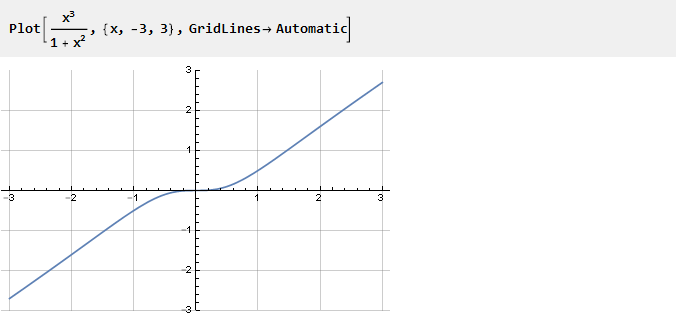
她不是偶然出现的。
如果从其中删除一个单元,则x
2将收缩,仅x将保留,即一条倾斜线。 因此,x的值越小,分母中单位的影响越大,从而产生我们需要的曲率。 考虑到此函数的不同比例,可以控制此曲率的程度:

因此,我们可以使用仅使用有理三阶多项式的刚度控制来重写以前的函数:
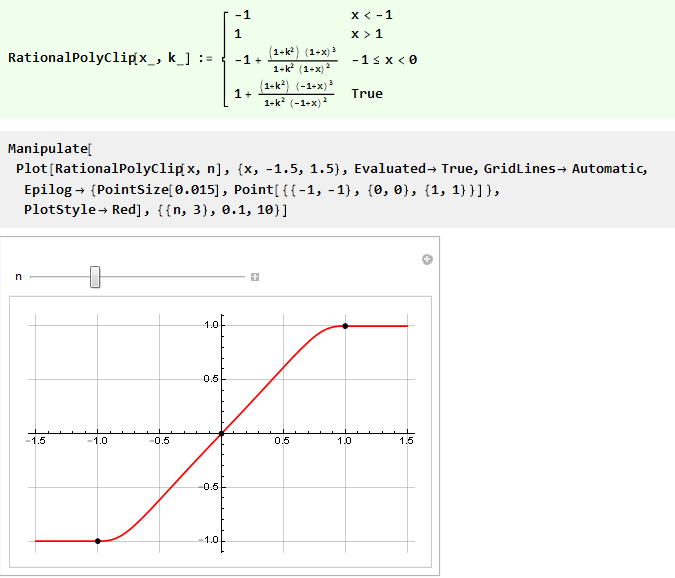
自动化
为了不每次都指定分段连续函数,我们可以定义一个辅助函数,以供体函数作为参数作为输入,自行执行此操作。
如果我们的函数已经具有对角线对称性并且已对准坐标中心(例如正弦波),那么我们可以简单地
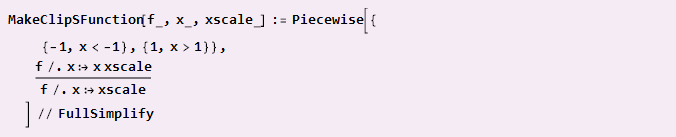
用法示例:

如果您需要从零件中组装,例如抛物线,并且坐标中心确定了对接点,则公式将稍微复杂一些:
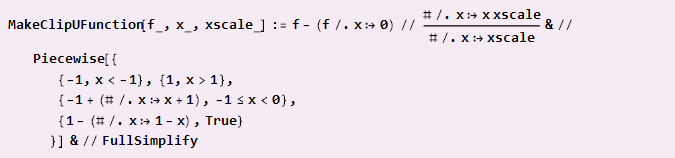
用法示例:

让我们继续参展
绝对可以使用任何函数来解决此问题,您只需要为其提供拐点即可。 以指数向下移动一个为例:
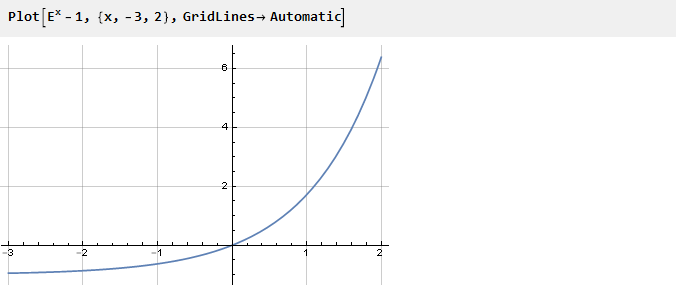
以前,为了确保在零点处发生必要的拐点,我们对函数求平方。 但是您可以采用另一种方法-例如,用另一个函数求和,该函数的零点导数的符号与指数的导数相反。 例如,-x:
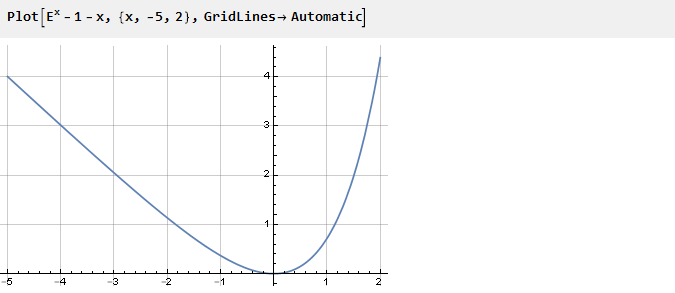
取决于曲线的哪一侧,函数的最终形式将取决于曲线。 现在,使用先前定义的辅助功能并选择边之一,我们得到:

要么

现在我们可以在一张图表上进行比较:
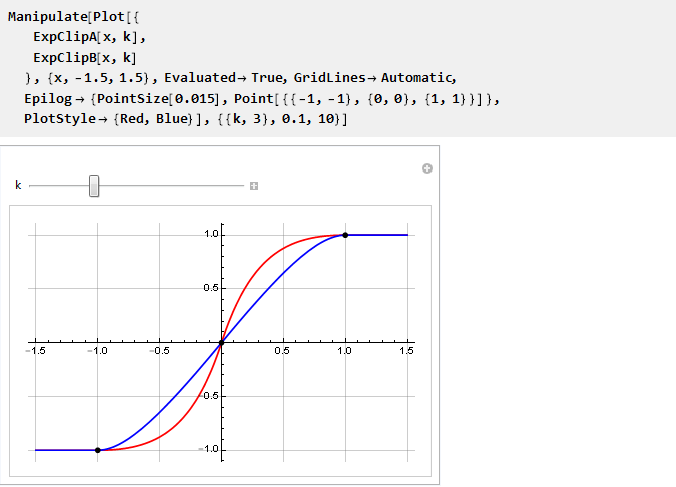
可以看出,当k→0时,它们趋于重合。 并且由于我们无法直接计算其值,因此我们将其除以零,因此将使用限制:

他们从我们已经知道的抛物线获得了分段函数。
打破对称
到目前为止,我们一直在考虑仅考虑对称函数。 但是,有时候我们不需要对称性-例如,模拟电子管放大器声音的失真。
取指数并将其乘以一个倒抛物线平方-得到与点-1和1处的横坐标轴的交点,同时确保二阶导数的平滑度; 通过缩放指数参数可以进行参数化:
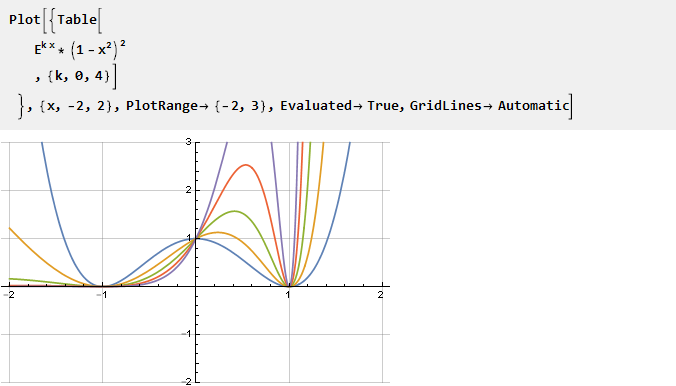
找到反导并将其缩放:
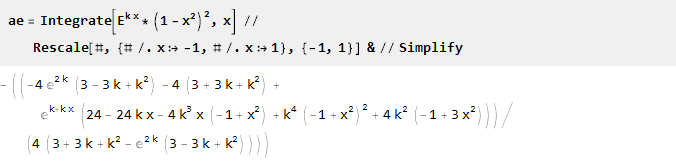
由于对于k = 0,我们得到除以零的值:

然后我们再找到极限

这是我们已经知道的三阶平滑多项式。 将所有内容组合成一个函数,我们得到
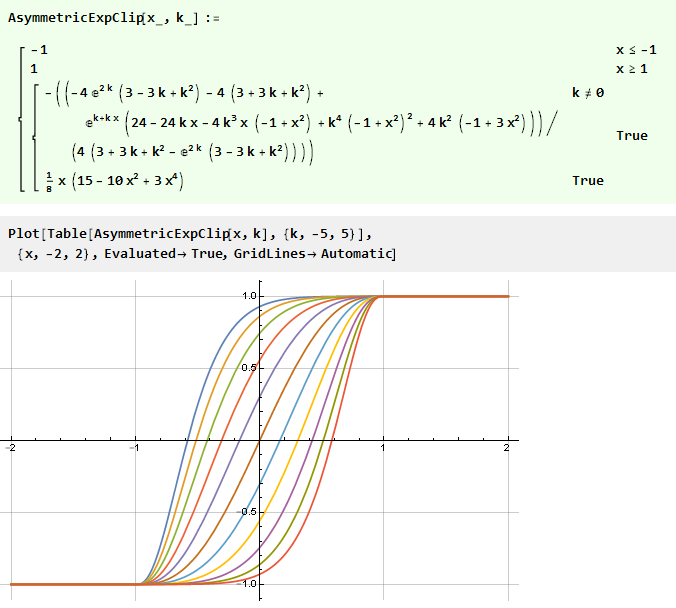
代替最初设计不对称函数的方法,您可以采用另一种方法-使用现成的对称函数,但是使用在区间{-1,1}上定义的附加曲线函数来“弯曲”该函数的值。
例如,考虑一个双曲线:
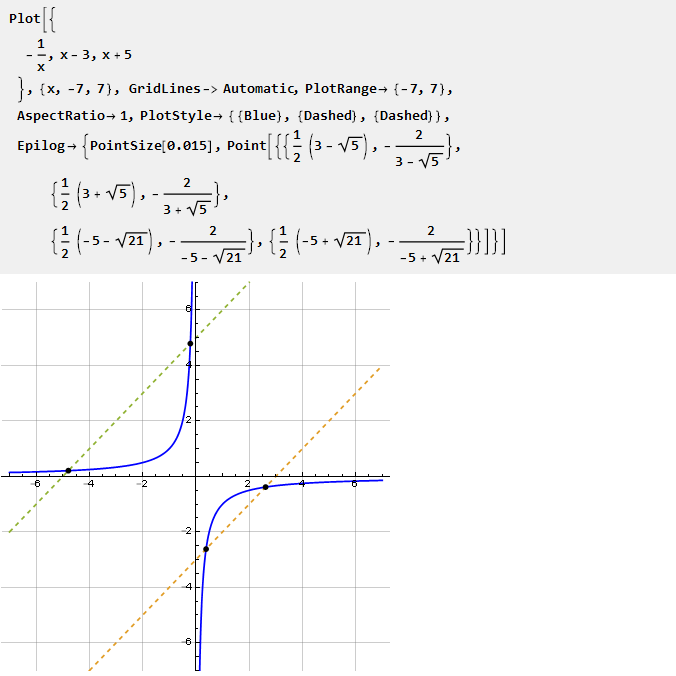
考虑到其分段的比例不同,可以在两个方向上调整曲率度。 如何找到此细分? 根据该图,可以寻找双曲线与直线的交点。 但是,由于这种相交并不总是存在,因此带来了一些困难。 因此,我们将走另一条路。
首先,将缩放因子添加到双曲线中:

然后我们将组成一个方程组,该方程组定义双曲线通过给定点的通过条件-其解将为我们提供感兴趣的系数:

现在,将解决方案替换为原始公式并简化:

让我们看看根据参数k得到的结果:
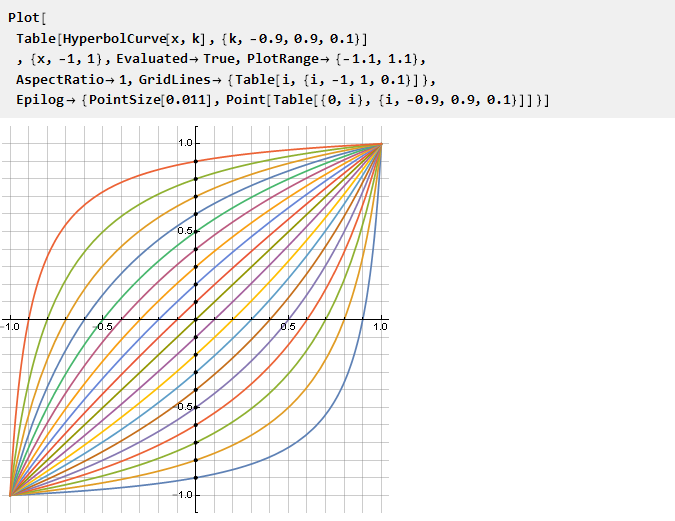
值得注意的是,对于k = 0,该公式自然会在x处折叠,并且不会出现特殊情况-尽管相对于初始夸张而言,它等效于零长度的段,一次等于两个。 同样引人注意的是,它的逆函数相同,但是参数为k:

现在我们可以使用它来修改任意约束函数,参数k从而设置与纵坐标轴的交点:
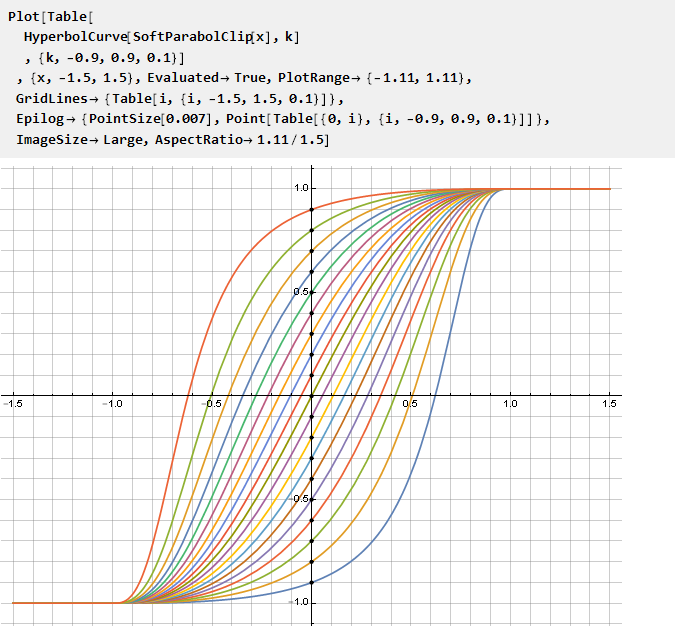
同样,您可以从其他函数(例如,具有可变基数的幂定律)构建曲线:
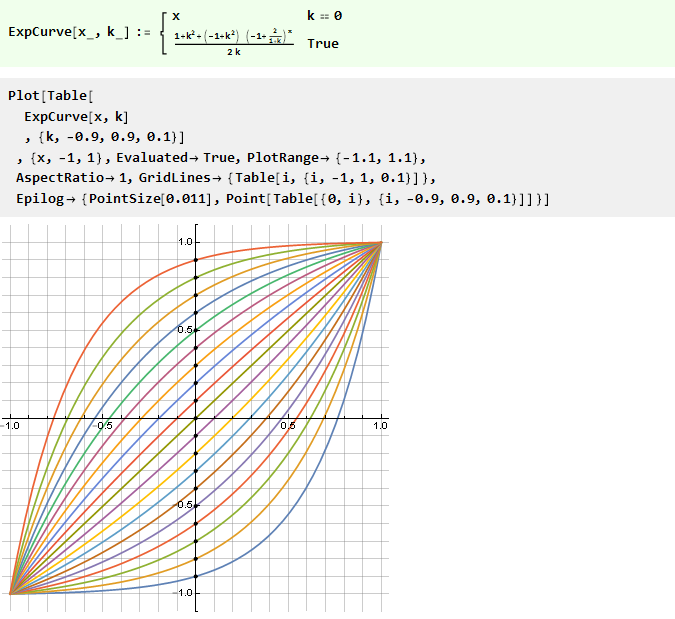
或它的倒数是对数的:
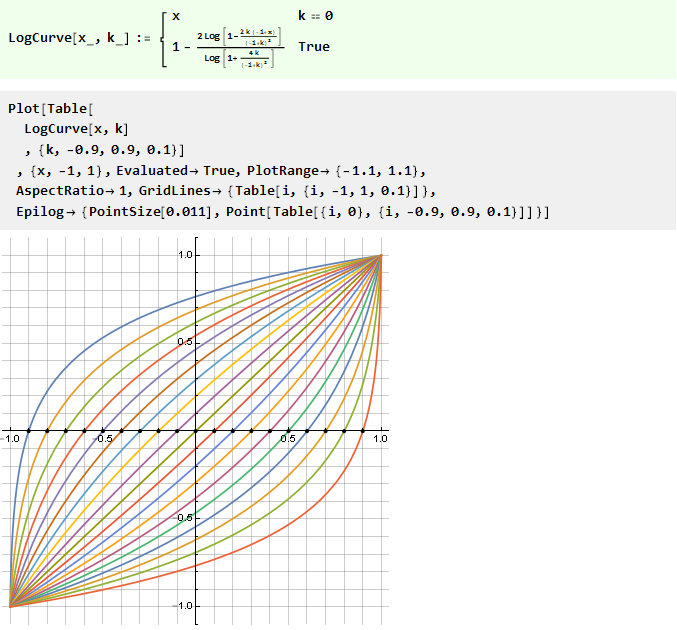
需要更高的准确性
我们可能希望在一定的时间间隔内确保函数的线性间距。 通过将直线引入分段连续函数来进行组织是合乎逻辑的,
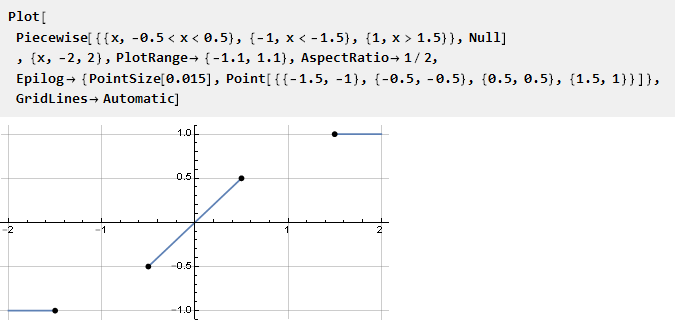
需要填写一些功能的空白处。 显然,对于具有线性截面的平滑对接,其一阶导数必须等于1。 以及所有后续(如果可能)零。 为了不重新推论这样的功能,我们可以采用现成的功能并将其适应此任务。 您还可以注意到,极限点的位置比统一点略远-这对于保持线性截面的斜率是必要的。
采用先前派生的PolySoft函数并将其移动,以使我们在坐标中心得到一个:
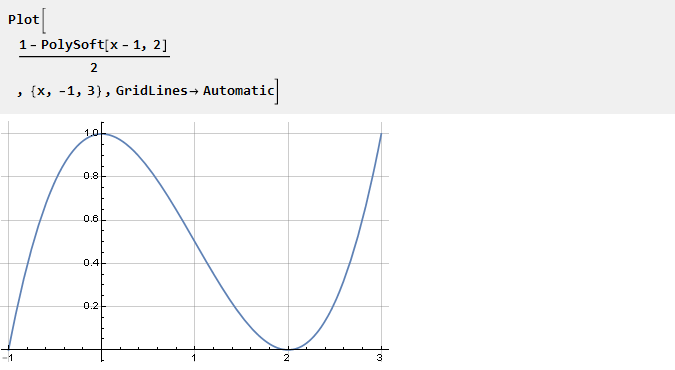
从其性质可以得出,在点0和点2的n-1个后续导数将等于零:
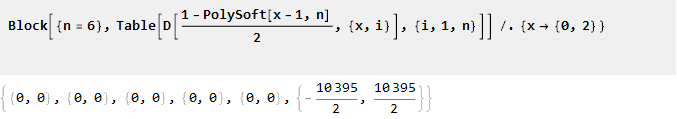
现在将其集成:
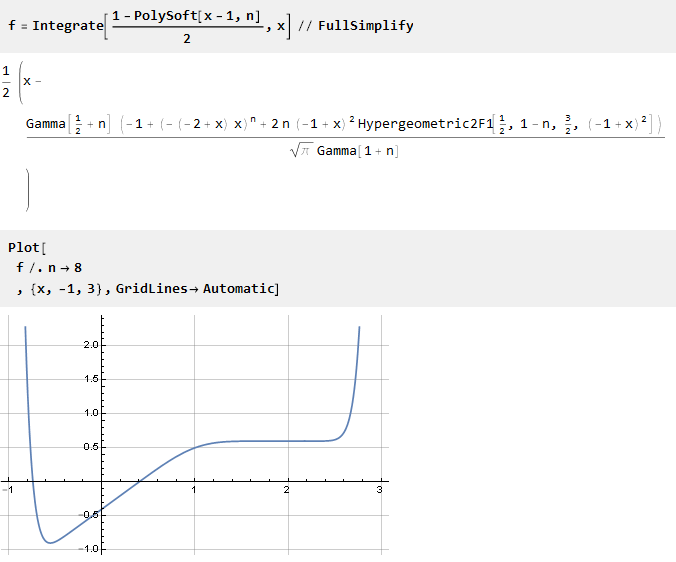
该功能相对于横坐标轴向下移动。 因此,有必要添加一个常数(等于函数在点0处的值)以组合坐标中心:

在这里,我们的n值为零。 它没有下降,因为没有定义零度中的零值。 我们可以手动将其删除,或者为简化起见,我们可以明确指出n大于零:

我们以防万一。 所有n的点0和2的值:

区间边缘的导数(对于5阶多项式):

如您所见,该功能非常麻烦。 为了不拖拽它并且不使计算复杂化,我们将继续使用特定的多项式进行操作,例如四阶:

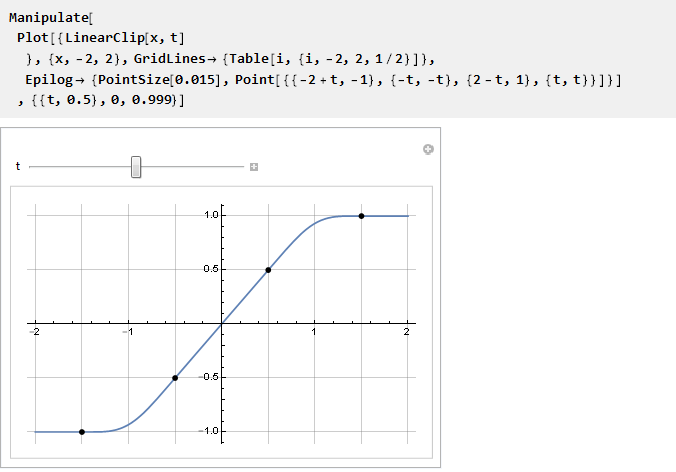
现在,您可以填充可用空间:

检查:
我们走向无限
有时可能需要趋向于一个单元却无法实现的功能。 维基百科
提供了几种著名的解决方案:
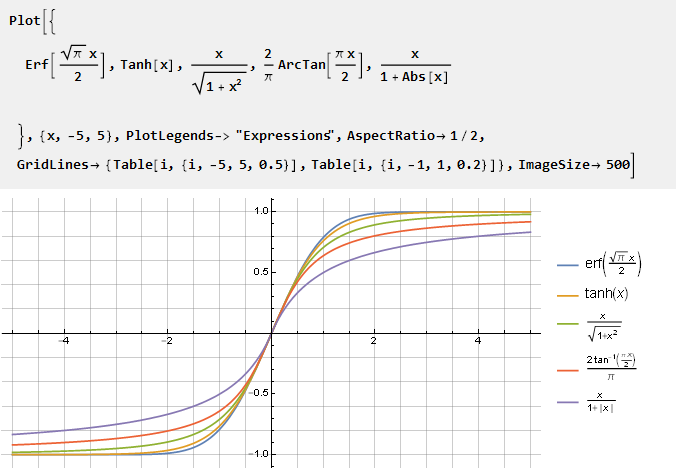
由于这些函数没有达到统一,因此相对于坐标中心的导数将它们标准化更方便。
我们可以使用对角线对称函数,通过其参数修改此类函数的形式,例如:
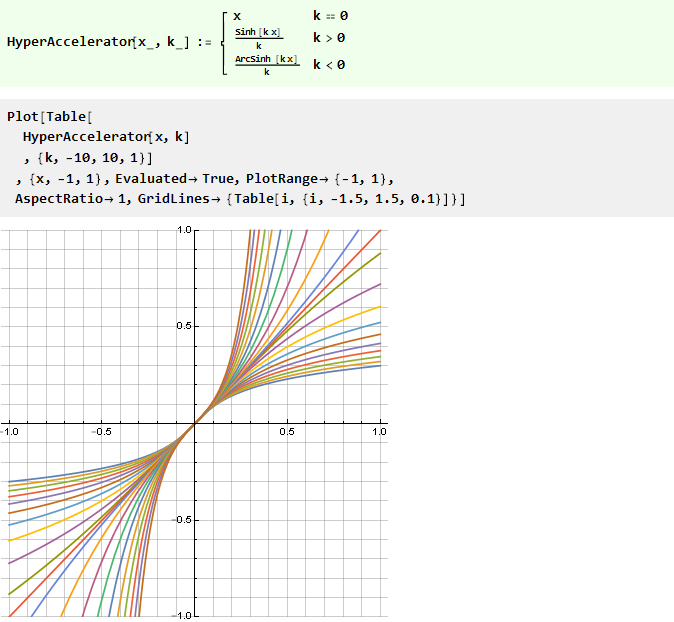
顺便说一句,这个函数本身也相反。
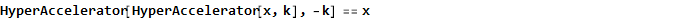
并且,以反正切为例,我们获得
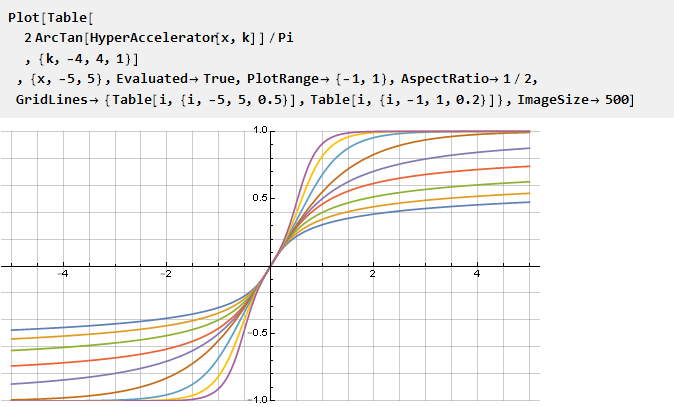
特别是在参数k = 1的情况下,将为我们提供
Guderman函数 。
如您所见,使用这种方法可以获得不希望的扭结,因此,更可取的是直接通过函数本身的属性来控制约束的刚度。 考虑几个带有参数的此类函数,为简洁起见,省略了其输出。
从幂函数:
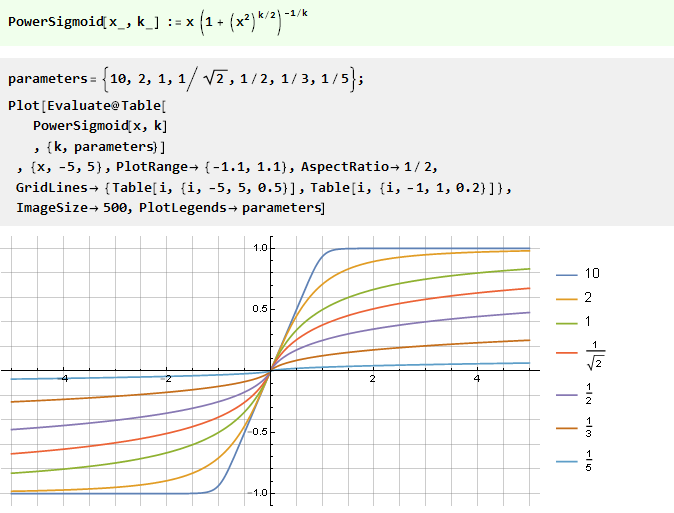
从两个具有偏移量的v形函数的总和中:
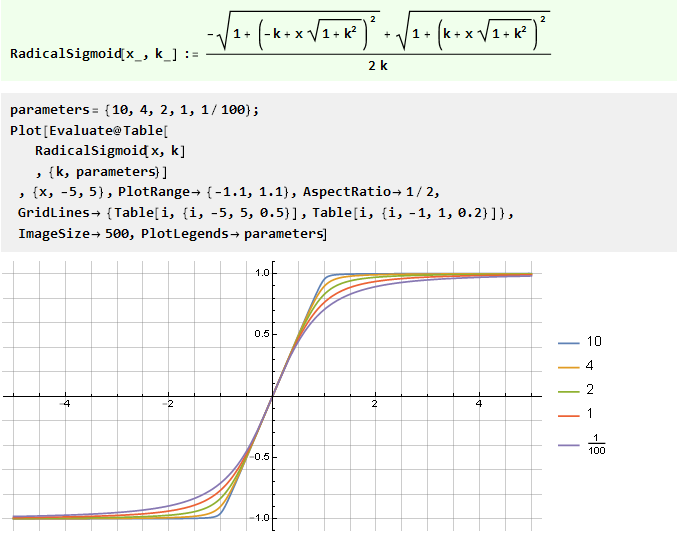
从广义误差函数:
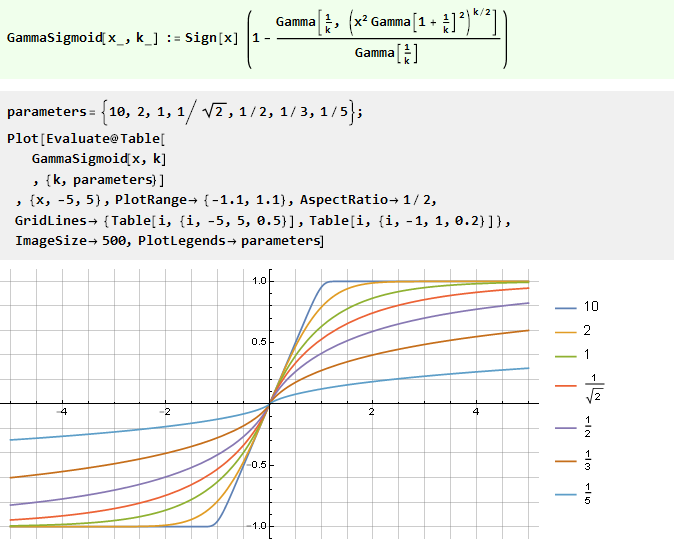
有理多项式的积分:
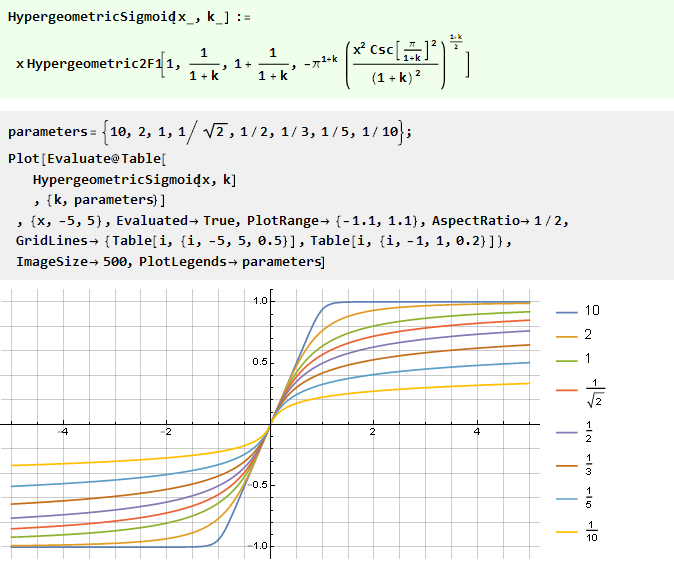
有趣的是,它的特殊情况是反正切的:

结论
构造此类函数可能是一项引人入胜的任务,在此过程中,将获得简单和复杂,漂亮和不太漂亮的公式。 看起来它们彼此非常相似,因此不需要这样的变化。 不一定是这种情况。
在其他刻度上(例如对数),差异可以更明显。 此外,除了标题中指示的任务之外,类似的功能也可以用于其他任务-混合信号,当一个信号的平滑衰减与另一个信号的平滑增大相结合时,或者构造声学滤波器-然后,耳朵会感觉到差异,或建立梯度-然后眼睛会察觉到差异。 此外,它们还可以用作其他更复杂功能(例如
window)的供体 。
总之,有必要澄清几点。
此处所有函数的定义范围是-1到1。如果需要其他范围(例如,从0到1),则可以很容易地手动重新计算:
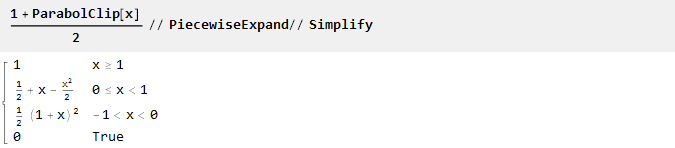
或使用内置的缩放功能:

为了方便将获得的公式导出到程序代码,CForm函数可能会很有用:
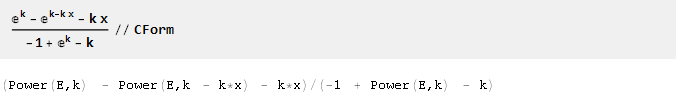
Mathematica源文件可以在
这里下载。
注意事项:
[1]真正的数学家当然可以严格证明(或反对)这一说法。
[2]在数学分析的标准过程中未考虑超几何函数。
[3]此重载仅针对字符单元定义; 浮点格式的单位(例如,绘制图形时)将不会被识别。