医生的警告。 当心这些难题。 副作用可能包括丢失下午的时间,皱巴巴的头发和惊叹号“啊,这就是这样做的方法”,声音太大,以致窗玻璃可能破裂。
几个月前,我在Twitter上遇到了
Katriona Shearer的数学难题。 他们立刻让我着迷:每个难题都是如此有形,手工制作的,仿佛是要解决这个难题。 对于每个人,您可以轻松地花费一个小时甚至更多的时间。
Katriona让我着迷于这些难题-并分享了她最喜欢的20个难题。 她甚至接受了采访,满足了我的好奇心和钦佩感(请参见文章结尾)。
好好享受 而且不要说医生没有警告。
1.上园时间
每个圆的哪一部分画完了? (等距的12个点;圆内唯一的点是圆心)
卡特里奥纳说:“不幸的是,在这六个人中,我所爱的人是唯一一个我自己还没有发明过的人,这是深蓝色的。”
2.倾斜的正方形
(对我来说,这是经典)。
3.这是一个陷阱
在矩形梯形中,绿色区域比黄色区域大6。
什么是x?“这是这个难题的“第二个版本”:比我提出的第一个版本要好。”
4.三个方形板
三个正方形的边的长度是连续的整数。
总面积是多少?“我真的很喜欢这个:我以此为基础绘制了许多漂亮的图案。”
5.美丽的发型
左下角正方形
的面积 5.
蓝色三角形的面积是多少?“可能是我一直以来的最爱。 看起来不可能! 在这里,解决方法称为“剪发”,即剪毛(不幸的是,不是我的荣幸)。
6.人人平等。
“我更喜欢原始版本的另一种更改。”
7.半圆陀螺
“带有角的拼图很难完成。 学生们说这是一个相当简单的任务,但是我的父母遇到了很大的困难。 看来这个难题需要更多的“知识”,但是解决过程本身更容易。”
8.电源和弦
圆的面积是多少?“在学校我没有学习相交和弦定理,所以我喜欢在任何地方使用它!”
9.两个圈子的故事
这些规则的多边形具有相同的周长。 找出内切圆的面积比。
“这是另一个难题的结果,但是我比原来更喜欢它!”
10.十月医生
阴影区域的值与正八边形的周长相同。
什么意思“我认为这是一项非常干净的任务,尽管它看起来像是埃德·索萨尔(Ed Southall)的难题中的一大堆。”
11.一切平方
“我喜欢这样一个事实,尽管您可以在这里找到橙色三角形的所有边(并且我在决定时就做到了),但实际上没有必要-有足够的面积和斜边。”
12.钉在蜂巢中
两个正六边形相同。 第三个面积为10。
红色三角形的面积是多少?“非常好:我喜欢您不必处理几乎可以肯定的任何边长。”
13.我看到了等腰
所有四个三角形都是等腰。
找到角落。“我认为解决这个问题是理想的。 许多人错过了重要信息,并得出结论说,有无数种解决方案!”
14.绿色vs蓝色
图片中还有更多绿色或蓝色(以及多少)吗?
“我最喜欢的另一个。”
15.石材切割机
在面积为12的正方形周围有四个等边三角形。
阴影区域是多少?“这里最好的是切开该区域的真正好的解决方案。”
16.骑,骑,离开拐角
在此正六边形上刻有六个相同的正方形和一个较小的矩形。
它们占据六边形的哪一部分?“这里的答案不是那么漂亮,但这确实让我感到惊讶。 我认为,由于其复杂性,这项任务没有像其他人那样在Twitter上得到如此广泛的传播!”
17.只有一个事实
这个广场的面积是多少?“这是我的最爱之一,因为起初看来信息还不够。”
18.洗衣机
大广场的哪一部分被填满了?“在这里,我喜欢正方形的混乱,因为它们就像在洗衣机中一样嗡嗡作响。 而且答案也非常漂亮。”
19.悬挂国旗
相同颜色的正方形具有相同的大小。
所有阴影区域的面积是多少?“一旦您了解了,它就非常简单-但是我不立即理解,因此答案的简单性让我感到惊讶。”
20.蒂格罗贡
该图的哪一部分画完了? 六边形是规则的,沿圆周均匀分布点。
“我很少发表这个。 但是图片让我想起了Tiger Tiger [来自凯洛格的速食早餐包-大约。 trans。]”。
奖励:
广场市落日
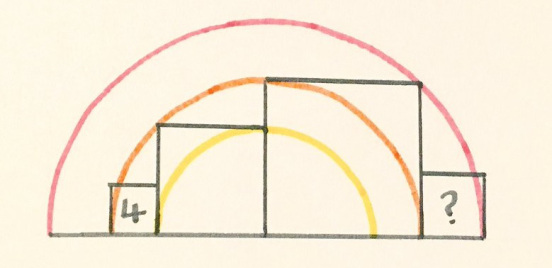
左边的正方形的面积为4。
右边的正方形的面积是多少?“我喜欢这个难题,它就像是广场城市上的日落。”
如果您是在读书开始后的6个月后才到这个地方读书的,并且桌子周围摆满了弄皱的纸和空的中国食物容器,那么您将很高兴阅读Katriona的简短采访。
您是如何发展难题的?我去苏格兰高地度假,但忘了穿外套,所以当我的朋友们在大自然中漫步时,我不得不独自坐在屋子里! 剩下的只有机械地在纸上画线。
我没想到它会变成一种爱好,但这有点让人上瘾,尤其是当人们寄回我喜欢的决定时。 您几乎总是可以精美地切出我错过的难题。
创作过程如何?这一切都始于绘制无意义的数字。 结果是整页的正方形以不同角度重叠正方形或带有不同阴影部分的正则(类型)五边形,然后查看是否存在良好的数学运算法则-长度,面积或角度之间的关系。
您的许多任务都是在纸上用记号笔绘制的。 为什么要这样?我尝试使用Desmos和Geogebra,但并不真正喜欢它。 我认为,经过几次反复试验后,手动绘制一个内切圆要比在软件几何中漂亮地构建一个内切圆更快。
另外,使用毡尖笔时,因为线条太粗,所以可以发明东西。 这是在“正确”看待,但又知道不能只拔出尺子并测量图形之间的良好折衷。
关于几何的好处之一是它可以宽恕很多。 我可以给您展示一个没有希望的正方形或圆形,但这足以传达这个概念,因为它们定义的很好。
您的某些难题提供的信息量最少。 您如何找到刚刚定义图表的边界?有时,这个最小值实际上是一个提示,因为它使您沿着同一条路前进。 我宁愿多给一些不必要的东西,所以有几种欺骗性的途径。 它还提供了更多的解决方案!
确实是这样,我发表了两个不可能的难题:幸运的是,通常有人会很快指出!
我还发布了包含大量冗余信息的难题,因为我看不到仅使用一半信息的好解决方案。
给潜在的拼图制作者的提示?好吧,我的冒名顶替综合症在这里得到了充分体现。 我绝对仍然是新手-我只是从8月才开始这样做[2018年10月发表文章-大约 每个]! 另一方面,我更喜欢创造难题和阅读解决方案,而不是自己解决难题。
难题的主要目标应该是娱乐性-这就是它与标准数学问题的区别所在。 因此,您至少需要三个中的两个:
- 问题的美丽陈述 。 提供最少的信息,以便读者对如何解决此类问题感兴趣。 或一些诱人的信息,据信每种信息都可以提供解决方案。 规则的多边形和圆形是奇妙的事情,因为它们隐藏了大量信息。
- 不错的方法 。 窍门或最短路径,或者突然的洞察力简化了一切。 这可能不是最明显的方法。 我看到了很多可以借助代数或无理数或带有pi的糟糕表达式可以解决的问题,最后一切都突然减少了-我知道有一种更简单的方法。
- 好的答案 。 为了最终得到一个丑陋的答案,研究拼图有点有趣。
基本上,开始绘制-找到您要解决的难题,然后考虑如何扩展它或更改某些元素。 如果您突然发现令您感到惊讶的比率,那么很有可能它们会使其他人感到惊讶。 Twitter是一个很棒的平台,因为人们可以发布自己的照片作为回应。