麻省理工学院。 讲座课程#6.858。 “计算机系统的安全性。” Nikolai Zeldovich,James Mickens。 2014年
计算机系统安全是一门有关开发和实施安全计算机系统的课程。 讲座涵盖了威胁模型,危害安全性的攻击以及基于最新科学研究的安全技术。 主题包括操作系统(OS)安全性,功能,信息流管理,语言安全性,网络协议,硬件安全性和Web应用程序安全性。
第1课:“简介:威胁模型”
第1 部分 /
第2 部分 /
第3部分第2课:“控制黑客攻击”,
第1 部分 /
第2 部分 /
第3部分第3讲:“缓冲区溢出:漏洞利用和保护”
第1 部分 /
第2 部分 /
第3部分讲座4:“特权分离”,
第1 部分 /
第2 部分 /
第3部分讲座5:“安全系统从何而来?”
第1 部分 /
第2部分讲座6:“机会”
第1 部分 /
第2 部分 /
第3部分讲座7:“本地客户端沙箱”
第1 部分 /
第2 部分 /
第3部分讲座8:“网络安全模型”
第1 部分 /
第2 部分 /
第3部分讲座9:“ Web应用程序安全性”
第1 部分 /
第2 部分 /
第3部分讲座10:“符号执行”
第1 部分 /
第2 部分 /
第3部分 现在,沿着分支向下,我们看到表达式t = y。 由于我们一次要考虑一条路径,因此我们不必为t引入新变量。 我们可以简单地说,由于t = y,因此t不再为0。
我们继续往下走,直到到达另一个分支。 为了进一步走这条路,我们必须做出什么新的假设? 这是假设t <y。
什么是t? 如果您查找右分支,我们将看到t = y。 在我们的表格中,T = y和Y = y。 从逻辑上可以得出结论,我们的约束看起来像y <y,不可能这样。
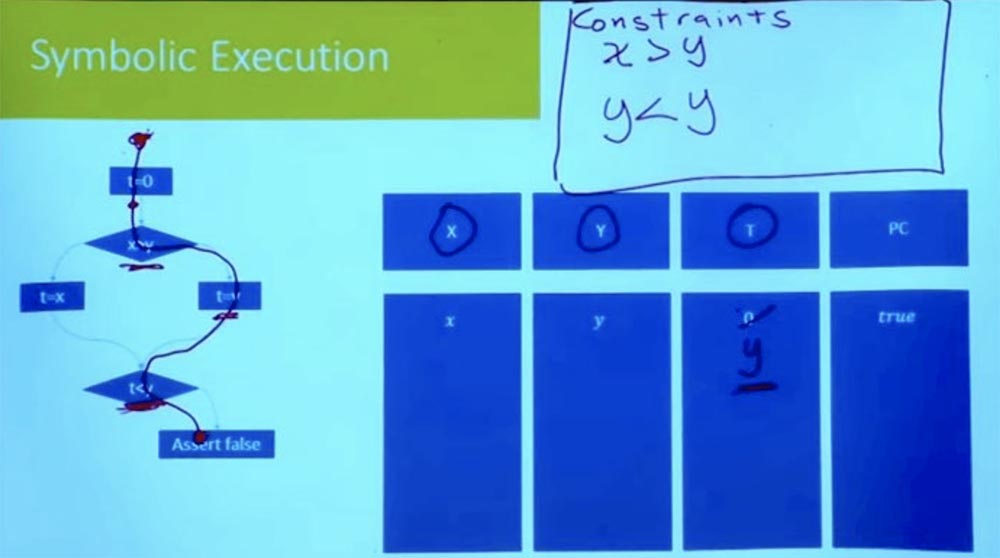
因此,我们一切都井然有序,直到达到t <y。 在我们得出错误的陈述之前,我们有所有不平等是正确的。 但这是行不通的,因为在执行右分支的任务时,我们存在逻辑上的不一致。
我们拥有通常所说的路径条件。 对于这种情况,程序必须满足此条件。 但是我们知道不能满足此条件,因此程序无法以这种方式运行。 因此,这条道路现在已被完全消除,我们知道这条正确的道路无法通过。
那怎么办呢? 让我们尝试以另一种方式遍历左侧分支。 这条路的条件是什么? 同样,我们的符号状态从t = 0开始,并且X和Y等于变量x和y。

在这种情况下,路径限制现在是什么? 我们将左分支表示为True,将右分支表示为False,并进一步考虑值t = x。 作为条件t = x,x> y和t <y的逻辑处理的结果,我们得出我们同时具有x> y和x <y。
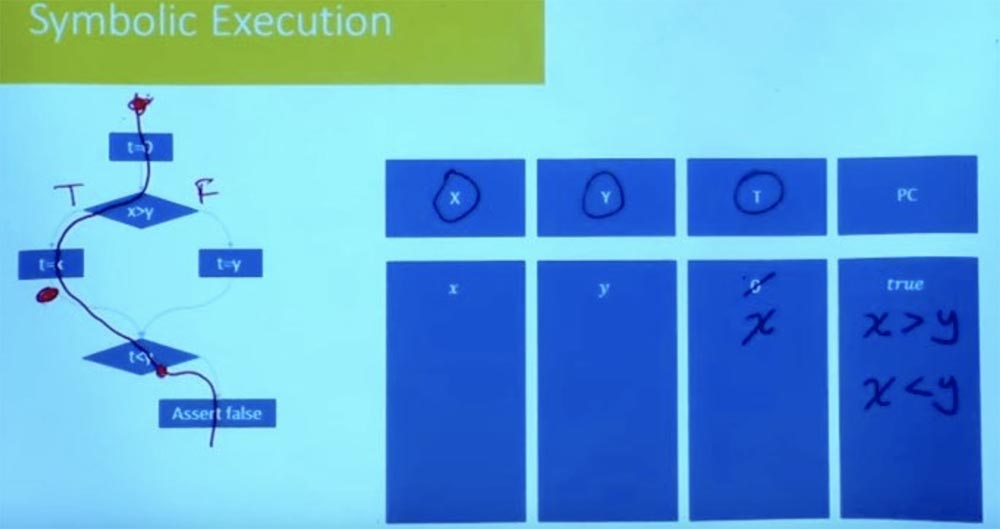
显然,该路径的条件是不令人满意的。 我们不能同时拥有大于和小于y的x。 没有分配满足两个约束的变量X。 因此,这告诉我们另一种方法也不令人满意。
事实证明,此刻,我们探索了程序中可能导致我们进入此状态的所有可能路径。 实际上,我们可以确定并验证没有任何可能的方式将我们引向错误陈述。
受众:在此示例中,您表明您研究了所有可能分支的程序进度。 但是符号执行的优点之一是我们不需要研究所有可能的指数路径。 那么在这个例子中如何避免这种情况呢?
教授:这是一个很好的问题。 在这种情况下,您需要在字符执行和想要的具体程度之间进行折衷。 因此,在这种情况下,与第一次在两个分支上同时查看程序流时相比,我们没有使用符号执行。 但是,由于此,我们的局限变得非常非常简单。
单个限制“一个接一个地”非常简单,但是您必须一次又一次地进行此操作,研究所有现有分支,并以指数方式以及所有可能的方式。
路径数量成倍增加,但对于每个路径整体而言,也有大量的输入数据可以通过该路径。 因此,这已经给您带来了很大的优势,因为您正在尝试各种可能的方法,而不是尝试所有可能的输入。 但是你能做得更好吗?
这是关于符号执行的大量实验的领域之一,例如,同时执行多个路径。 在讲座材料中,您遇到了试探法和实验者用来使搜索更容易解决的一组策略。
例如,他们要做的一件事是,他们一个接一个地探索,但不要完全盲目地做。 他们在执行每个步骤后都会检查路径条件。 假设在我们的程序中,不是说“ false”,而是有一个复杂的程序树,即控制流程图。
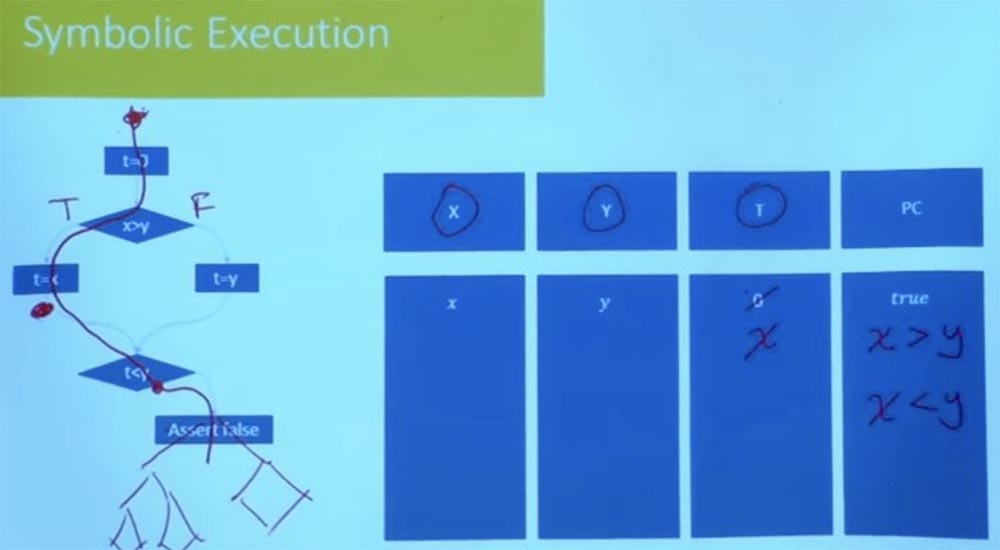
您无需等到最后就可以验证此路径是否可行。 在那一刻,当您达到条件t <y时,您已经知道这条路径是不令人满意的,并且您将永远不会朝那个方向前进。 因此,在程序开始时切除错误的分支会减少经验工作量。 合理探索路径可防止将来发生程序失败的可能性。 今天使用的许多实用工具主要是从随机测试开始,以获取初始路径集,然后,他们将开始探索附近的路径。 他们为可能在每个分支执行程序而处理了许多选项,想知道这些路径上会发生什么。
如果我们有一套很好的测试,它就特别有用。 您运行测试,发现这部分代码没有执行。 因此,您可以采用最接近代码实现的路径,并询问是否可以更改此路径,以便其朝正确的方向前进?

但是,当您尝试同时创建所有路径时,限制开始变得棘手。 因此,您可以做的是一次执行一项功能,而您可以一起学习一项功能中的所有路径。 如果您尝试制作大型积木,则通常可以探索所有可能的方法。
最重要的是,对于每个分支机构,您都要检查自己的限制并确定该分支机构是否真的可以双向发展。 如果她不能走两条路,那么不走在她不能走的方向上可以节省时间和精力。 另外,我不记得他们用来寻找更有可能产生非常好的结果的方法的具体策略。 但是在初始阶段切断错误的分支非常重要。
到目前为止,我们主要讨论的是“玩具代码”,整数变量,分支以及非常简单的东西。 但是,当您拥有更复杂的程序时会怎样? 特别是当您的程序中包含一堆程序时会发生什么?

从历史上看,髋关节堆一直是所有软件分析的祸根,因为当您尝试使用左右分配内存的C程序运行它们时,Fortran时代的干净优雅的东西会完全爆炸。 那里有叠加层以及与该程序相关联的所有混乱,这些程序具有分配的内存和算术指针。 这是符号执行具有出色的程序推理能力的领域之一。
那么我们该怎么做呢? 让我们暂时忽略分支和控制流。 我们这里有一个简单的程序。 它分配一些内存,使其无效,并从指针x获取新的指针y。 然后她向y写一些东西,并检查指针y中存储的值是否等于指针x中存储的值?
基于C的基本知识,您可以看到由于x重置且y = 25,所以未执行此检查,因此x表示不同的位置。 到目前为止,我们一切都很好。
我们对堆进行建模的方式以及在大多数系统上对堆进行建模的方式都使用C语言中的堆表示形式,其中它只是一个巨大的地址基,一个可以在其中放置数据的巨大数组。
这意味着我们可以将程序表示为非常大的全局数据集,称为MEM。 这实际上是一个将地址映射到值的数组。 地址只是一个64位值。 当您从该地址读取某些内容后会发生什么? 这取决于您如何对内存建模。
如果在字节级别对其进行建模,则会得到一个字节。 如果在单词级别对其建模,那么您会得到一个单词。 根据您感兴趣的错误类型以及是否关心内存分配,您将对其建模有些不同,但是通常,内存只是一个从地址到值的数组。

因此,地址只是一个整数。 从某种意义上说,C对地址的看法无关紧要,它只是一个64位或32位整数,具体取决于您的计算机。 它只是在此存储器中索引的值。 而您可以放入内存的内容,则可以从该内存中读取。
因此,指针算术之类的东西就变成了整数算术。 实际上,存在一些困难,因为在C语言中,指针算法会知道指针类型,并且指针类型将与大小成比例地增加。 因此,我们得到以下行:
y = x + 10; sizeof(int)

但是真正重要的是,当您写入和读取内存时会发生什么。 基于应该在y中写入25的指针,我获取了一个内存数组,并用y对其进行了索引。 然后我将25写入此存储位置。
然后,我继续执行语句MEM [y] = MEM [x],从内存中的位置y读取值,从内存中的位置x读取值,并将它们相互比较。 因此,我检查它们是否匹配。
这是一个非常简单的假设,允许您从使用堆的程序切换到使用代表内存的巨大全局数组的程序。 这意味着现在,在谈论管理堆的程序时,您实际上不需要谈论管理堆的程序。 您将完美地谈论数组,而不是堆。
这是另一个简单的问题。 那malloc函数呢? 您只需采用C语言中的malloc实现并使用它,跟踪所有突出显示的页面,跟踪所有已释放的内容,只有一个空闲列表就足够了。 事实证明,出于多种目的和多种错误,您不需要使malloc变得复杂。
实际上,您可以从如下所示的malloc切换到x = malloc(sizeof(int)* 100):
POS = 1
整数malloc(整数n){
rv = POS
POS + = n;
}
简单地说:“我将在内存中保存下一个可用空间的计数器,每当有人要求提供地址时,我都会给他这个位置并增加这个位置,然后返回rv。” 在这种情况下,完全忽略了传统意义上的malloc。

在这种情况下,不会释放内存。 该功能只是继续从内存中越来越远地移动,并且越来越远,这就是它在没有任何释放的情况下结束的地方。 她也不十分在意内存中哪些地方不值得写,因为有一些特殊的地址保留给操作系统使用。
当您尝试讨论执行指针操作的某种复杂代码时,它不会为使malloc函数的编写变得复杂的任何模型建模。
同时,您并不在意释放内存,但是您担心程序是否要在缓冲区之外进行写操作,在这种情况下,此malloc函数可能会很好。

当您执行实际代码的符号执行时,这实际上非常经常发生。 一个非常重要的步骤是对库的功能进行建模。 对库函数进行建模的方式,一方面将对分析的性能和可伸缩性产生巨大影响,但另一方面,也会影响准确性。
因此,如果您有一个像这样的“玩具”模型malloc,它将非常迅速地执行操作,但是同时会出现某些类型的错误,您不会注意到。 因此,例如,在此模型中,我完全忽略了分布,因此如果有人可以访问未分配的空间,则可能会出错。 因此,在现实生活中,我永远不会使用这种米奇malloc模型。
因此,它始终是分析准确性和效率之间的平衡。 而且,标准函数(例如malloc get)的模型越复杂,其分析的可扩展性就越差。 但是对于某些错误类别,您将需要这些简单的模型。 因此,C语言中的各种库都非常重要,这对于理解此类程序的实际作用至关重要。
因此,我们通过对带有数组的程序进行推理,从而减少了对堆进行推理的问题,但是我并没有真正告诉您如何谈论带有数组的程序。 事实证明,大多数SMT求解器都支持阵列理论。

这个想法是,如果a是一个数组,那么会有一些表示法允许您采用此数组并创建一个新数组,其中位置i更新为值e。 清楚吗?
因此,如果我有一个数组a,然后执行此更新操作,然后尝试读取k的值,则这意味着如果k与i不同,则k的值将等于数组a中k的值,并且它将等于e,如果k等于i。
更新阵列意味着您需要使用旧阵列并用新阵列更新它。 好吧,如果您有一个包含数组理论的公式,这就是为什么我从零数组开始的原因,零数组在任何地方都简单地用零表示。

然后我将5写入位置i,将7写入位置j,此后我从k读取并检查它是否为5。 然后可以使用定义来扩展它,例如:“如果k是i,k是y,而k与j不同,那么是5,否则就不会。 5“。
在实践中,SMT求解器不仅将其扩展为许多布尔公式,而且还在SAT求解器和引擎之间使用这种来回策略,从而能够谈论阵列理论来开展这项工作。
重要的是,依靠数组的这种理论,使用与生成整数公式相同的策略,您实际上可以生成包括数组逻辑,数组更新,数组轴,数组迭代的公式。 只要您纠正路径,这些公式就很容易生成。
如果您不更正路径,而是想创建一个与程序沿所有路径通过相对应的公式,那么这也相对容易。 您唯一需要处理的是一种特殊的循环。
使用未定义的函数,字典和地图也很容易建模。 实际上,数组理论本身只是一个不确定函数的特例。 借助这些功能,可以完成更复杂的事情。 在现代的SMT求解器中,内置了对集合和集合操作进行推理的支持,如果您正在谈论包含计算集合的程序,这将非常有用。
在设计这些工具之一时,建模阶段非常重要。 重点不仅在于如何根据理论对复杂的程序功能进行建模,例如将堆减少为数组之类的事情。 关键还在于您使用了哪些理论和求解器。 有大量具有不同关系的理论和求解器,因此有必要在效率和成本之间做出合理的折衷。

大多数实用工具都遵循位向量理论,并且如有必要,可以使用数组理论对堆进行建模。 通常,实用工具会尽量避免使用更复杂的理论,例如集合论。 这是因为,如果您不使用真正需要这种工具才能工作的程序,则在某些情况下它们的可伸缩性通常较低。
受众:除了研究象征性表现外,开发人员还关注什么?
: — , . , , , , . , .
, , . , , , , , , , .
, — , , . , , — , JavaScript Python, . , .

, Python. , , : «, , , ». .
, , , , , .
, , , - , , .
, , , . , , Microsoft Word, , , .
, , , , .
, . , , - , - . , , . , .
该课程的完整版本可
在此处获得 。
, . ? ? ,
30% entry-level , : VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps $20 ? ( RAID1 RAID10, 24 40GB DDR4).
VPS(KVM)E5-2650 v4(6核)10GB DDR4 240GB SSD 1Gbps至12月免费,在六个月内付款,您可以
在此处订购。
Dell R730xd 2 ? 2 Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100 $249 ! . c Dell R730xd 5-2650 v4 9000 ?