🌽 🆑 ✋🏾 博弈论：科特林的事例决策 ➰ 🎊 ✔️

博弈论是一门数学学科，它考虑对有目标的玩家的行为进行建模，这是为冲突中的行为选择最佳策略。在Habré上，已经讨论了该主题，但是今天我们将更详细地讨论其某些方面，并考虑有关Kotlin的示例。

因此，策略是一组规则，这些规则根据情况确定每个个人举动的选择。最佳玩家策略是确保给定游戏中最佳位置的策略，即最大增益。如果游戏重复了几次，并且除了个人随机移动之外，最佳策略还会提供最大的平均获胜率。

博弈论的任务是确定玩家的最佳策略。基于找到最佳策略的主要假设是，对手（一个或多个）并不比玩家本人聪明，并且会尽一切努力来实现自己的目标。合理对手的计算只是冲突中潜在的位置之一，但是在博弈论中，正是它奠定了基础。

在一些自然的游戏中，只有一名参与者最大化他们的利润。自然博弈是数学模型，其中解决方案的选择取决于客观现实。例如，消费者需求，自然状态等。 “自然”是不追求自己目标的对手的广义概念。在这种情况下，将使用多个条件来选择最佳策略。
自然游戏中有两种类型的任务：

当自然界接受每种可能状态的概率已知时，在风险条件下做出决策的任务；
在无法获得有关自然状态发生概率的信息的不确定性条件下的决策任务。

这里简要介绍这些标准。

现在，我们将考虑纯策略中的决策标准，并且在本文结尾处，我们将通过分析方法解决混合策略中的博弈。

订座

我不是博弈论专家，但是在这项工作中，我第一次使用了Kotlin。但是，我决定分享我的结果。如果您发现文章有误或想提供建议，请在PM中。

问题陈述

我们将通过一个例子来分析所有决策标准。任务是这样的：农民需要确定以何种比例种植三种农作物，这些农作物的产量以及因此的利润是否取决于夏天的状态：凉爽多雨，正常还是干热。农民根据天气从1公顷土地上的不同农作物计算了净利润。游戏由以下矩阵确定：

此外，我们将以策略的形式介绍此矩阵：

（ ） ， （ ） ， （ ， ）

$U_ {1} =（0,2,5），U_ {2} =（2,3,1），U_ {3} =（4,3，-1）$

所需的最佳策略表示为

$u_ {opt}$ 。在不确定的情况下，我们将使用Wald，乐观，悲观，野蛮和Hurwitz的标准在风险情况下使用贝叶斯和拉普拉斯的标准来解决游戏。

如上所述，示例将在Kotlin上进行。我注意到，通常会有诸如Gambit（用C编写），Axelrod和PyNFG（用Python编写）之类的解决方案，但是我们将骑着自己的脚踏车组装在膝盖上，只是为了戳破一些时尚，时髦和青年编程语言。

为了以编程方式实现游戏的解决方案，我们将介绍几个类。首先，我们需要一个允许我们描述游戏矩阵的行或列的类。该类非常简单，并包含可能值（替代值或自然状态）及其对应名称的列表。 key段将用于标识以及比较，在实现优势时将需要进行比较。

游戏矩阵行或列

 import java.text.DecimalFormat import java.text.NumberFormat open class GameVector(name: String, values: List<Double>, key: Int = -1) : Comparable<GameVector> { val name: String val values: List<Double> val key: Int private val formatter:NumberFormat = DecimalFormat("#0.00") init { this.name = name; this.values = values; this.key = key; } public fun max(): Double? { return values.max(); } public fun min(): Double? { return values.min(); } override fun toString(): String{ return name + ": " + values .map { v -> formatter.format(v) } .reduce( {f1: String, f2: String -> "$f1 $f2"}) } override fun compareTo(other: GameVector): Int { var compare = 0 if (this.key == other.key){ return compare } var great = true for (i in 0..this.values.lastIndex){ great = great && this.values[i] >= other.values[i] } if (great){ compare = 1 }else{ var less = true for (i in 0..this.values.lastIndex){ less = less && this.values[i] <= other.values[i] } if (less){ compare = -1 } } return compare } }

游戏矩阵包含有关替代方案和自然状态的信息。此外，它还实现了一些方法，例如，找到主导集和游戏的净价。

游戏矩阵

 open class GameMatrix(matrix: List<List<Double>>, alternativeNames: List<String>, natureStateNames: List<String>) { val matrix: List<List<Double>> val alternativeNames: List<String> val natureStateNames: List<String> val alternatives: List<GameVector> val natureStates: List<GameVector> init { this.matrix = matrix; this.alternativeNames = alternativeNames this.natureStateNames = natureStateNames var alts: MutableList<GameVector> = mutableListOf() for (i in 0..matrix.lastIndex) { val currAlternative = alternativeNames[i] val gameVector = GameVector(currAlternative, matrix[i], i) alts.add(gameVector) } alternatives = alts.toList() var nss: MutableList<GameVector> = mutableListOf() val lastIndex = matrix[0].lastIndex //       ,     for (j in 0..lastIndex) { val currState = natureStateNames[j] var states: MutableList<Double> = mutableListOf() for (i in 0..matrix.lastIndex) { states.add(matrix[i][j]) } val gameVector = GameVector(currState, states.toList(), j) nss.add(gameVector) } natureStates = nss.toList() } open fun change (i : Int, j : Int, value : Double) : GameMatrix{ var mml = this.matrix.toMutableList() var rowi = mml[i].toMutableList() rowi.set(j, value) mml.set(i, rowi) return GameMatrix(mml.toList(), alternativeNames, natureStateNames) } open fun changeAlternativeName (i : Int, value : String) : GameMatrix{ var list = alternativeNames.toMutableList() list.set(i, value) return GameMatrix(matrix, list.toList(), natureStateNames) } open fun changeNatureStateName (j : Int, value : String) : GameMatrix{ var list = natureStateNames.toMutableList() list.set(j, value) return GameMatrix(matrix, alternativeNames, list.toList()) } fun size() : Pair<Int, Int>{ return Pair(alternatives.size, natureStates.size) } override fun toString(): String { return " :\n" + natureStateNames.reduce { n1: String, n2: String -> "$n1;\n$n2" } + "\n :\n" + alternatives .map { a: GameVector -> a.toString() } .reduce { a1: String, a2: String -> "$a1;\n$a2" } } protected fun dominateSet(gvl: List<GameVector>, list: MutableList<String>, dvv: Int) : MutableSet<GameVector>{ var dSet: MutableSet<GameVector> = mutableSetOf() for (gv in gvl){ for (gvv in gvl){ if (!dSet.contains(gv) && !dSet.contains(gvv)) { if (gv.compareTo(gvv) == dvv) { dSet.add(gv) list.add("[$gvv]  [$gv]") } } } } return dSet } open fun newMatrix(dCol: MutableSet<GameVector>, dRow: MutableSet<GameVector>) : GameMatrix{ var result: MutableList<MutableList<Double>> = mutableListOf() var ralternativeNames: MutableList<String> = mutableListOf() var rnatureStateNames: MutableList<String> = mutableListOf() val dIndex = dCol.map { c -> c.key }.toList() for (i in 0 .. natureStateNames.lastIndex){ if (!dIndex.contains(i)){ rnatureStateNames.add(natureStateNames[i]) } } for (gv in this.alternatives){ if (!dRow.contains(gv)){ var nr: MutableList<Double> = mutableListOf() for (i in 0 .. gv.values.lastIndex){ if (!dIndex.contains(i)){ nr.add(gv.values[i]) } } result.add(nr) ralternativeNames.add(gv.name) } } val rlist = result.map { r -> r.toList() }.toList() return GameMatrix(rlist, ralternativeNames.toList(), rnatureStateNames.toList()) } fun dominateMatrix(): Pair<GameMatrix, List<String>>{ var list: MutableList<String> = mutableListOf() var dCol: MutableSet<GameVector> = dominateSet(this.natureStates, list, 1) var dRow: MutableSet<GameVector> = dominateSet(this.alternatives, list, -1) val newMatrix = newMatrix(dCol, dRow) var ddgm = Pair(newMatrix, list.toList()) val ret = iterate(ddgm, list) return ret; } protected fun iterate(ddgm: Pair<GameMatrix, List<String>>, list: MutableList<String>) : Pair<GameMatrix, List<String>>{ var dgm = this var lddgm = ddgm while (dgm.size() != lddgm.first.size()){ dgm = lddgm.first list.addAll(lddgm.second) lddgm = dgm.dominateMatrix() } return Pair(dgm,list.toList().distinct()) } fun minClearPrice(): Double{ val map: List<Double> = this.alternatives.map { a -> a?.min() ?: 0.0 } return map?.max() ?: 0.0 } fun maxClearPrice(): Double{ val map: List<Double> = this.natureStates.map { a -> a?.max() ?: 0.0 } return map?.min() ?: 0.0 } fun existsClearStrategy() : Boolean{ return minClearPrice() >= maxClearPrice() } }

我们描述符合条件的接口

标准

 interface ICriteria { fun optimum(): List<GameVector> }

不确定性下的决策

面对不确定性做出决策表明，玩家不会受到理性对手的反对。

沃尔德准则

Wald准则使可能的最坏结果最大化：

$u_ {opt} = max_ {i} min_ {j} [U]$

使用该标准可以确保避免出现最坏的结果，但是这种策略的代价是失去了获得最佳结果的机会。

考虑一个例子。对于策略

（ ） ， （ ） ， （ ， ）

$U_ {1} =（0,2,5），U_ {2} =（2,3,1），U_ {3} =（4,3，-1）$ 找到低点并获得下三个

（ ， ， ）

$S =（0，1，-1）$ 。所指示三元组的最大值将是值1，因此，根据Wald准则，获胜策略是该策略

$U_ {2} =（2,3,1）$ 对应于种植文化2。

Wald准则的软件实现很简单：

 class WaldCriteria(gameMatrix : GameMatrix) : ICriteria { val gameMatrix: GameMatrix init{ this.gameMatrix = gameMatrix } override fun optimum(): List<GameVector> { val mins = gameMatrix.alternatives.map { a -> Pair(a, a.min()) } val max = mins.maxWith( Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!)}) return mins .filter { m -> m.second == max!!.second } .map { m -> m.first } } }

为了清楚起见，我将第一次展示该解决方案看起来像一个测试：

测验

 private fun matrix(): GameMatrix { val alternativeNames: List<String> = listOf(" 1", " 2", " 3") val natureStateNames: List<String> = listOf("  ", "", "  ") val matrix: List<List<Double>> = listOf( listOf(0.0, 2.0, 5.0), listOf(2.0, 3.0, 1.0), listOf(4.0, 3.0, -1.0) ) val gm = GameMatrix(matrix, alternativeNames, natureStateNames) return gm; } } private fun testCriteria(gameMatrix: GameMatrix, criteria: ICriteria, name: String){ println(gameMatrix.toString()) val optimum = criteria.optimum() println("$name.  : ") optimum.forEach { o -> println(o.toString()) } } @Test fun testWaldCriteria() { val matrix = matrix(); val criteria = WaldCriteria(matrix) testCriteria(matrix, criteria, " ") }

不难猜测，对于其他条件，差异仅在于criteria对象的创建。

乐观准则

当使用乐观主义者的标准时，玩家会选择给出最佳结果的解决方案，而乐观主义者则认为游戏的条件将对他最有利：

$u_ {opt} = max_ {i} max_ {j} [U]$

当最大供应量与最小需求量相吻合时，乐观主义者的策略可能会导致负面后果-公司注销未售出的产品时可能会蒙受损失。同时，乐观主义者的策略也具有一定的意义，例如，您不需要照顾不满意的客户，因为任何可能的需求都会得到满足，因此无需维护客户的位置。如果实现了最大需求，那么乐观主义者的策略将使您获得最大的效用，而其他策略将导致利润损失。这提供了一定的竞争优势。

考虑一个例子。对于策略

$U_ {1} =（0,2,5），U_ {2} =（2,3,1），U_ {3} =（4,3，-1）$ 找到，找到最大值，然后得到下三个

$S =（5，3，4）$ 。所指示的三元组的最大值将是值5，因此，根据乐观标准，获胜策略是策略

$U_ {1} =（0.2.5）$ 对应于种植文化1。

乐观准则的实施与Wald准则几乎没有什么不同：

 class WaldCriteria(gameMatrix : GameMatrix) : ICriteria { val gameMatrix: GameMatrix init{ this.gameMatrix = gameMatrix } override fun optimum(): List<GameVector> { val mins = gameMatrix.alternatives.map { a -> Pair(a, a.min()) } val max = mins.maxWith( Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!)}) return mins .filter { m -> m.second == max!!.second } .map { m -> m.first } } }

悲观主义的标准

此标准旨在从可能的最小元素中选择游戏矩阵的最小元素：

$u_ {opt} = min_ {i} min_ {j} [U]$

悲观主义的标准表明事件的发展将对决策者不利。当使用此标准时，决策者会受到对情况可能失去控制的指导，因此，他试图通过选择收益最低的期权来消除潜在风险。

考虑一个例子。对于策略

$U_ {1} =（0,2,5），U_ {2} =（2,3,1），U_ {3} =（4,3，-1）$ 找到，找到最小值，然后得到下三个

$S =（0，1，-1）$ 。所指示的三元组的最小值将是值-1，因此，根据悲观情绪的准则，获胜策略是

$U_ {3} =（4.3，-1）$ 对应于种植文化3。

在了解Wald的标准和乐观情绪之后，很容易猜出悲观主义标准的类别将是什么样子：

 class PessimismCriteria(gameMatrix : GameMatrix) : ICriteria { val gameMatrix: GameMatrix init{ this.gameMatrix = gameMatrix } override fun optimum(): List<GameVector> { val mins = gameMatrix.alternatives.map { a -> Pair(a, a.min()) } val min = mins.minWith( Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!)}) return mins .filter { m -> m.second == min!!.second } .map { m -> m.first } } }

野蛮准则

野蛮标准（悲观悲观主义者的标准）涉及最大程度地减少最大的利润损失，换句话说，最大的后悔是最大程度地减少了利润损失：

$u_ {opt} = min_ {i} max_ {j} [S] \\ s_ {i，j} =（max \ begin {bmatrix} u_ {1，j} \\ u_ {2，j} \\。 .. \\ u_ {n，j} \ end {bmatrix}-u_ {i，j}）$

在这种情况下，S是后悔矩阵。

从上一步发现的遗憾中，根据Savage准则得出的最佳解决方案应使后悔最少。与找到的实用程序相对应的解决方案将是最佳的。

所获得解决方案的特征包括最大的失望保证不存在，以及其他玩家最大可能获胜的保证减少。

考虑一个例子。对于策略

$U_ {1} =（0,2,5），U_ {2} =（2,3,1），U_ {3} =（4,3，-1）$ 后悔矩阵：

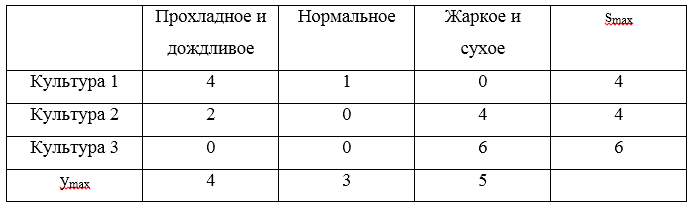
三个最大的遗憾

$S =（4,4,6）$ 。这些风险的最小值为4，与策略相对应

$U_ {1}$ 和

$U_ {2}$ 。

编程Savage测试要困难一些：

 class SavageCriteria(gameMatrix: GameMatrix) : ICriteria { val gameMatrix: GameMatrix init { this.gameMatrix = gameMatrix } fun GameMatrix.risk(): List<Pair<GameVector, Double?>> { val maxStates = this.natureStates.map { n -> Pair(n, n.values.max()) } .map { n -> n.first.key to n.second }.toMap() var am: MutableList<Pair<GameVector, List<Double>>> = mutableListOf() for (a in this.alternatives) { var v: MutableList<Double> = mutableListOf() for (i in 0..a.values.lastIndex) { val mn = maxStates.get(i) v.add(mn!! - a.values[i]) } am.add(Pair(a, v.toList())) } return am.map { m -> Pair(m.first, m.second.max()) } } override fun optimum(): List<GameVector> { val risk = gameMatrix.risk() val minRisk = risk.minWith(Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!) }) return risk .filter { r -> r.second == minRisk!!.second } .map { m -> m.first } } }

赫维兹准则

Hurwitz标准是极端悲观主义和完全乐观主义者之间的有条不紊的折衷方案：

$u_ {opt} = max（\ gamma×A（k）+ A（0）×（1-\ gamma））$

A（0）是极端悲观主义者的策略，A（k）是完全乐观主义者的策略，

$\伽马= 1$ -权重系数的设定值：

$0 \ leq \伽马\ leq1$ ;

$\伽马= 0$ -极端悲观主义

$\伽马= 1$ -完全乐观。

通过少量离散策略，可以设置权重系数的期望值

$\伽玛$ ，然后考虑执行的离散化，将结果四舍五入到最接近的可能值。

考虑一个例子。对于策略

$U_ {1} =（0,2,5），U_ {2} =（2,3,1），U_ {3} =（4,3，-1）$ 。我们假设乐观系数

$\伽玛= $ 0.$ 。现在制作一张桌子：

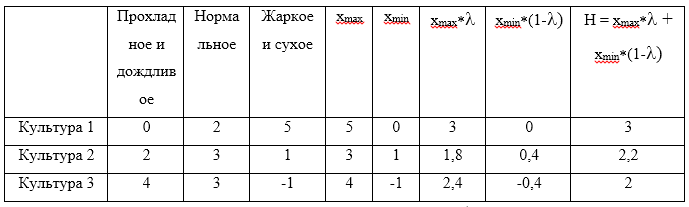
计算出的H的最大值将是3，对应于策略

$U_ {1}$ 。

Hurwitz标准的实施已经非常繁琐：

 class HurwitzCriteria(gameMatrix: GameMatrix, optimisticKoef: Double) : ICriteria { val gameMatrix: GameMatrix val optimisticKoef: Double init { this.gameMatrix = gameMatrix this.optimisticKoef = optimisticKoef } inner class HurwitzParam(xmax: Double, xmin: Double, optXmax: Double){ val xmax: Double val xmin: Double val optXmax: Double val value: Double init{ this.xmax = xmax this.xmin = xmin this.optXmax = optXmax value = xmax * optXmax + xmin * (1 - optXmax) } } fun GameMatrix.getHurwitzParams(): List<Pair<GameVector, HurwitzParam>> { return this.alternatives.map { a -> Pair(a, HurwitzParam(a.max()!!, a.min()!!, optimisticKoef)) } } override fun optimum(): List<GameVector> { val hpar = gameMatrix.getHurwitzParams() val maxHurw = hpar.maxWith(Comparator { o1, o2 -> o1.second.value.compareTo(o2.second.value) }) return hpar .filter { r -> r.second == maxHurw!!.second } .map { m -> m.first } } }

风险决策

决策方法可以根据风险条件下的决策标准，但必须符合以下条件：

缺乏有关可能后果的可靠信息；
存在概率分布；
了解每个决策的结果或后果的可能性。

如果在风险条件下做出决策，则备选决策的成本将通过概率分布来描述。在这方面，该决策基于预期价值标准的使用，根据该标准，比较各种替代解决方案，以实现预期利润最大化或预期成本最小化。

可以降低期望值的标准，以最大化期望（平均）利润或最小化期望成本。在这种情况下，假定与每个替代解决方案关联的利润（成本）是随机变量。

这些任务的制定通常如下：在随机事件影响行动结果的情况下，一个人选择任何行动。但是玩家对这些事件的可能性有一定的了解，可以计算出最有利可图的动作组合和顺序。

为了继续给出示例，我们用概率补充游戏矩阵：

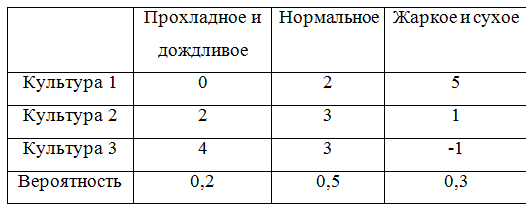
为了考虑概率，必须重做一些描述游戏矩阵的类。事实证明，这不是很优雅，但是很好。

带有概率的博弈矩阵

 open class ProbabilityGameMatrix(matrix: List<List<Double>>, alternativeNames: List<String>, natureStateNames: List<String>, probabilities: List<Double>) : GameMatrix(matrix, alternativeNames, natureStateNames) { val probabilities: List<Double> init { this.probabilities = probabilities; } override fun change (i : Int, j : Int, value : Double) : GameMatrix{ val cm = super.change(i, j, value) return ProbabilityGameMatrix(cm.matrix, cm.alternativeNames, cm.natureStateNames, probabilities) } override fun changeAlternativeName (i : Int, value : String) : GameMatrix{ val cm = super.changeAlternativeName(i, value) return ProbabilityGameMatrix(cm.matrix, cm.alternativeNames, cm.natureStateNames, probabilities) } override fun changeNatureStateName (j : Int, value : String) : GameMatrix{ val cm = super.changeNatureStateName(j, value) return ProbabilityGameMatrix(cm.matrix, cm.alternativeNames, cm.natureStateNames, probabilities) } fun changeProbability (j : Int, value : Double) : GameMatrix{ var list = probabilities.toMutableList() list.set(j, value) return ProbabilityGameMatrix(matrix, alternativeNames, natureStateNames, list.toList()) } override fun toString(): String { var s = "" val formatter: NumberFormat = DecimalFormat("#0.00") for (i in 0 .. natureStateNames.lastIndex){ s += natureStateNames[i] + " = " + formatter.format(probabilities[i]) + "\n" } return " :\n" + s + " :\n" + alternatives .map { a: GameVector -> a.toString() } .reduce { a1: String, a2: String -> "$a1;\n$a2" } } override fun newMatrix(dCol: MutableSet<GameVector>, dRow: MutableSet<GameVector>) : GameMatrix{ var result: MutableList<MutableList<Double>> = mutableListOf() var ralternativeNames: MutableList<String> = mutableListOf() var rnatureStateNames: MutableList<String> = mutableListOf() var rprobailities: MutableList<Double> = mutableListOf() val dIndex = dCol.map { c -> c.key }.toList() for (i in 0 .. natureStateNames.lastIndex){ if (!dIndex.contains(i)){ rnatureStateNames.add(natureStateNames[i]) } } for (i in 0 .. probabilities.lastIndex){ if (!dIndex.contains(i)){ rprobailities.add(probabilities[i]) } } for (gv in this.alternatives){ if (!dRow.contains(gv)){ var nr: MutableList<Double> = mutableListOf() for (i in 0 .. gv.values.lastIndex){ if (!dIndex.contains(i)){ nr.add(gv.values[i]) } } result.add(nr) ralternativeNames.add(gv.name) } } val rlist = result.map { r -> r.toList() }.toList() return ProbabilityGameMatrix(rlist, ralternativeNames.toList(), rnatureStateNames.toList(), rprobailities.toList()) } } }

贝叶斯准则

贝叶斯标准（期望标准）用于风险条件下的决策问题，作为对策略的评估

$u_ {i}$ 出现相应随机变量的数学期望。根据此规则，最佳球员策略

$u_ {opt}$ 从以下条件中找到：

$u_ {opt} = max_ {1 \ leq i \ leq n} M（u_ {i}）\\ M（u_ {i}）= max_ {1 \ leq i \ leq n} \ sum_ {j = 1} ^ m u_ {i，j} \ cdot y_ {j} ^ 0$

换句话说，策略效率低下的指标

$u_ {i}$ 根据贝叶斯准则，关于风险的是矩阵第i行的风险的平均值（期望）

$inline$ 其概率与自然的概率一致。那么，基于贝叶斯准则的纯策略中关于风险的最优策略

$u_ {opt}$ 低效率，即平均风险最小。关于收益和相对于风险的贝叶斯准则是等效的，即如果策略

$u_ {opt}$ 相对于获胜而言，贝叶斯准则是最优的，然后针对风险而言是贝叶斯准则的最优，反之亦然。

让我们继续该示例并计算数学期望值：

$M_1 = 0 \ cdot0.2 +2 \ cdot0.5 +5 \ cdot0.3 = 2.5; \\ M_2 = 2 \ cdot0.2 +3 \ cdot0.5 +1 \ cdot0.3 = 2.2 ; \\ M_4 = 0 \ cdot0.2 +3 \ cdot0.5 +（-1）\ cdot0.3 = 2.0;$

最高数学期望是

$M_1$ 因此，制胜策略就是策略

$U_1$ 。

贝叶斯准则的软件实现：

 class BayesCriteria(gameMatrix: ProbabilityGameMatrix) : ICriteria { val gameMatrix: ProbabilityGameMatrix init { this.gameMatrix = gameMatrix } fun ProbabilityGameMatrix.bayesProbability(): List<Pair<GameVector, Double?>> { var am: MutableList<Pair<GameVector, Double>> = mutableListOf() for (a in this.alternatives) { var alprob: Double = 0.0 for (i in 0..a.values.lastIndex) { alprob += a.values[i] * this.probabilities[i] } am.add(Pair(a, alprob)) } return am.toList(); } override fun optimum(): List<GameVector> { val risk = gameMatrix.bayesProbability() val maxBayes = risk.maxWith(Comparator { o1, o2 -> o1.second!!.compareTo(o2.second!!) }) return risk .filter { r -> r.second == maxBayes!!.second } .map { m -> m.first } } }

拉普拉斯准则

当需求水平的等概率假设成立时，拉普拉斯准则对效用的数学期望进行了简化的最大化，从而消除了收集真实统计数据的需要。

在一般情况下，使用拉普拉斯准则时，期望效用矩阵和最佳准则确定如下：

$u_ {opt} = max [\上线{U}] \\ \上线{U} = \开始{bmatrix} \上线{u} _ {1} \\ \上线{u} _ {2} \\。 .. \\ \上划线{u} _ {n} \结束{bmatrix}，\上划线{u} _ {i} = \ frac {1} {n} \ sum_ {j = 1} ^ nu_ {i，j }$

考虑以拉普拉斯准则进行决策的示例。我们计算每种策略的算术平均值：

$\ overline {u} _ {1} = \ frac {1} {3} \ cdot（0 + 2 + 5）= 2.3 \\ \ overline {u} _ {2} = \ frac {1} { 3} \ cdot（2 + 3 + 1）= 2.0 \\ \上线{u} _ {3} = \ frac {1} {3} \ cdot（4 + 3-1）= $ 2.$

所以制胜策略就是策略

$U_1$ 。

拉普拉斯标准的软件实现：

 class LaplaceCriteria(gameMatrix: GameMatrix) : ICriteria { val gameMatrix: GameMatrix init { this.gameMatrix = gameMatrix } fun GameMatrix.arithemicMean(): List<Pair<GameVector, Double>> { return this.alternatives.map { m -> Pair(m, m.values.average()) } } override fun optimum(): List<GameVector> { val risk = gameMatrix.arithemicMean() val maxBayes = risk.maxWith(Comparator { o1, o2 -> o1.second.compareTo(o2.second) }) return risk .filter { r -> r.second == maxBayes!!.second } .map { m -> m.first } } }

混合策略。分析方法

分析方法使您可以用混合策略解决游戏。为了制定一种通过分析方法找到游戏解的算法，我们考虑了一些其他概念。

策略策略

主导战略

$U_{i}$

（如果有）

$U_{i-1}$

$u_{1..n} \in U_{i} \geq u_{1..n} \in U_{i-1}$ 。换句话说，如果在支付矩阵的一行中所有元素都大于或等于另一行中的相应元素，则第一行将主导第二行，并被称为主导行。而且，如果支付矩阵的某一列中的所有元素都小于或等于另一列的相应元素，则第一列将主导第二列，并称为主导列。

游戏的最低价称为

$\alpha = max_i min_j u_{ij}$ 。
游戏的最高价称为

$\beta = min_j max_i u_{ij}$ 。

现在，您可以通过解析方法制定一种解决游戏的算法：

计算底部和上 $\alpha$ 游戏价格。如果 $\beta$ ，然后用纯策略写下答案；否则，继续求解 $\alpha = \beta$
删除主导行主导列。可能有几个。在最佳策略中，其对应的成分将为0
通过线性编程解决矩阵游戏。

为了举例，您需要提供一个描述解决方案的类

解决

 class Solve(gamePriceObr: Double, solutions: List<Double>, names: List<String>) { val gamePrice: Double val gamePriceObr: Double val solutions: List<Double> val names: List<String> private val formatter: NumberFormat = DecimalFormat("#0.00") init{ this.gamePrice = 1 / gamePriceObr this.gamePriceObr = gamePriceObr; this.solutions = solutions this.names = names } override fun toString(): String{ var s = " : " + formatter.format(gamePrice) + "\n" for (i in 0..solutions.lastIndex){ s += "$i) " + names[i] + " = " + formatter.format(solutions[i] / gamePriceObr) + "\n" } return s } fun itersect(matrix: GameMatrix): String{ var s = " : " + formatter.format(gamePrice) + "\n" for (j in 0..matrix.alternativeNames.lastIndex) { var f = false val a = matrix.alternativeNames[j] for (i in 0..solutions.lastIndex) { if (a.equals(names[i])) { s += "$j) " + names[i] + " = " + formatter.format(solutions[i] / gamePriceObr) + "\n" f = true break } } if (!f){ s += "$j) " + a + " = 0\n" } } return s } }

以及通过单纯形方法执行解决方案的类。由于我不懂数学，因此使用了Apache Commons Math的现成实现。

解算器

 open class Solver (gameMatrix: GameMatrix) { val gameMatrix: GameMatrix init{ this.gameMatrix = gameMatrix } fun solve(): Solve{ val goalf: List<Double> = gameMatrix.alternatives.map { a -> 1.0 } val f = LinearObjectiveFunction(goalf.toDoubleArray(), 0.0) val constraints = ArrayList<LinearConstraint>() for (alt in gameMatrix.alternatives){ constraints.add(LinearConstraint(alt.values.toDoubleArray(), Relationship.LEQ, 1.0)) } val solution = SimplexSolver().optimize(f, LinearConstraintSet(constraints), GoalType.MAXIMIZE, NonNegativeConstraint(true)) val sl: List<Double> = solution.getPoint().toList() val solve = Solve(solution.getValue(), sl, gameMatrix.alternativeNames) return solve } }

现在，我们通过解析方法执行解决方案。为了清楚起见，我们采用另一个游戏矩阵：

$\begin{pmatrix} 2& 4& 8& 5 \\ 6& 2& 4& 6\\ 3& 2& 5& 4 \end{pmatrix}$

该矩阵中有一个主导集：

$\begin{pmatrix} 2& 4\\ 6& 2\end{pmatrix}$

解决方案

 val alternativeNames: List<String> = listOf(" 1", " 2", " 3") val natureStateNames: List<String> = listOf("  ", "", "  ", "") val matrix: List<List<Double>> = listOf( listOf(2.0, 4.0, 8.0, 5.0), listOf(6.0, 2.0, 4.0, 6.0), listOf(3.0, 2.0, 5.0, 4.0) ) val gm = GameMatrix(matrix, alternativeNames, natureStateNames) val (dgm, list) = gm.dominateMatrix() println(dgm.toString()) println(list.reduce({s1, s2 -> s1 + "\n" + s2})) println() val s: Solver = Solver(dgm) val solve = s.solve() println(solve)

游戏解决方案

以相等的价格游戏3.33

$(0,33; 0,67; 0)$

而不是结论

我希望本文对那些对自然游戏的解决方案有初步了解的人有所帮助。而不是结论，而是指向GitHub的链接。

谢谢您的建设性反馈！

博弈论：科特林的事例决策