Geekly articles weekly

多臂强盗问题-比较Epsilon-Greedy策略和Thompson抽样

哈Ha！ 我向您介绍了解决多臂匪徒的首页：epsilon-greedy和Thompson抽样的比较 。

多臂匪徒问题


多臂匪徒问题是解决方案科学中最基本的任务之一。 即，这是在不确定条件下资源的最佳分配的问题。 “多臂匪”这个名称本身来自由手柄控制的旧老虎机。 这些突击步枪被昵称为“土匪”，因为与他们交谈后，人们通常会感到被抢。 现在想象一下，有几台这样的机器，而与其他汽车对抗的机会也不同。 自从我们开始使用这些机器以来，我们想确定哪个机会更高，并且比其他机器更频繁地使用该机器。


问题是：我们如何最有效地了解哪台机器最适合，同时实时尝试许多功能？ 这不是某种理论上的问题，而是企业一直面临的问题。 例如，对于需要向用户显示的消息，公司有几个选项（例如，消息包括广告，网站，图像），以便所选消息最大化特定业务任务（转换，可点击性等）。


解决此问题的一种典型方法是多次运行A / B测试 。 也就是说，花几个星期来平均显示每个选项，然后根据统计测试确定哪个选项更好。 此方法适用于很少的选项（例如2或4）。但是，当选项很多时，此方法将变得无效-既浪费时间，又损失利润。


浪费时间的来源应该很容易理解。 更多选项-需要更多的A / B测试-需要更多时间来做出决定。 利润损失的发生并不那么明显。 机会损失（机会成本）-与我们执行一项行动而不是执行另一项行动（即简单而言）有关的成本，这就是我们投资A而不是投资B所损失的。投资B是投资损失的利润在A中。与选项检查相同。 在完成A / B测试之前，请勿中断它们。 这意味着在测试结束之前，实验者不知道哪个选项更好。 但是，仍然相信一种选择会比另一种更好。 这意味着，通过延长A / B测试，我们不会为足够多的访客显示最佳选择（尽管我们不知道哪个选择不是最佳选择），从而损失了我们的利润。 这是A / B测试失去的好处。 如果只有一个A / B测试，那么损失的利润可能根本就不算大。 大量的A / B测试意味着长期以来，我们不得不向客户展示很多并非最佳选择。 如果您可以实时地快速丢弃不良选项，那就更好了，只有这样，当剩下的选项很少时，才对它们使用A / B测试。


采样器或代理是快速测试和优化选项分配的方法。 在本文中，我将向您介绍汤普森采样及其属性。 我还将汤普森采样与epsilon-greedy算法进行比较，epsilon-greedy算法是多臂匪徒问题的另一种流行选择。 一切都将从头开始用Python实现-所有代码都可以在这里找到。


简要概念词典


  • 代理，采样器，匪徒（ 代理，采样器，匪徒 ）-一种算法，用于决定要显示的选项。
  • 变体-访问者看到的消息的另一种变体。
  • 动作-算法选择的动作（显示哪个选项）。
  • 使用（ 利用 ）-根据可用数据做出选择以使总奖励最大化。
  • 探索， 探索 -做出选择以更好地了解每个选项的回报。
  • 奖励，积分（ 分数，奖励 ）-业务任务，例如转换或可点击性。 为简单起见，我们认为它是二项分布的，并且等于1或0-单击或不单击。
  • 环境-代理运行的上下文-选项和对用户隐藏的“回报”。
  • 投资回报率，成功概率（回报率 ）-一个隐藏变量，等于获得分数的概率= 1，对于每个选项来说，它都是不同的。 但是用户看不到她。
  • 尝试（ 试用 ）-用户访问页面。
  • 后悔是所有可用选项的最佳结果与当前尝试中可用选项的结果之间的区别。 对已经采取的行动感到后悔的次数越少越好。
  • 讯息（ message ）-横幅，页面选项以及其他我们想要尝试的不同版本。
  • 采样-根据给定分布生成样本。

探索和利用


代理是寻求实时决策方法的算法，目的是在探索选择空间与使用最佳选择之间取得平衡。 这种平衡非常重要。 必须调查选项的空间，以了解哪个选项是最佳的。 如果我们首先发现了这个最佳选择，然后一直使用它，那么我们将使环境中可获得的总回报最大化。 另一方面，我们也想探索其他可能的选择-如果将来它们会变得更好，那又会怎样呢，但我们还不知道呢？ 换句话说，我们希望避免可能的损失，尝试尝试一些次优的选择，以便自己弄清其回报。 如果他们的回报实际上更高，则可以更频繁地展示它们。 探索方案的另一个好处是，我们不仅可以更好地理解平均投资回报率，而且可以更好地理解投资回报率的分布范围，即可以更好地估算不确定性。
因此，主要问题是要解决-解决勘探与开发（探索与开发权衡）之间的难题的最佳方法是什么。


Epsilon-贪婪算法


解决这个难题的典型方法是epsilon-greedy算法。 “贪婪”是指您的想法。 经过一段初始时间后，当我们意外进行尝试（例如，尝试1000次）时，该算法会急于选择e ％的尝试来选择最佳选项k。 例如，如果e = 0.05，则算法在95％的时间内选择最佳选项，而在其余5％的时间内选择随机尝试。 实际上，这是一个相当有效的算法，但是，它可能不足以探索期权的空间，因此，评估哪个期权是最佳的，卡在次优期权上是不够的。 让我们在代码中展示该算法的工作原理。


但是首先，一些依赖性。 我们必须定义环境。 这是算法将在其中运行的上下文。 在这种情况下，上下文非常简单。 他呼叫代理，以便代理决定选择哪个操作，然后上下文启动该操作，并将为该操作收到的要点返回给代理（后者以某种方式更新了他的状态）。


class Environment: def __init__(self, variants, payouts, n_trials, variance=False): self.variants = variants if variance: self.payouts = np.clip(payouts + np.random.normal(0, 0.04, size=len(variants)), 0, .2) else: self.payouts = payouts #self.payouts[5] = self.payouts[5] if i < n_trials/2 else 0.1 self.n_trials = n_trials self.total_reward = 0 self.n_k = len(variants) self.shape = (self.n_k, n_trials) def run(self, agent): """Run the simulation with the agent. agent must be a class with choose_k and update methods.""" for i in range(self.n_trials): # agent makes a choice x_chosen = agent.choose_k() # Environment returns reward reward = np.random.binomial(1, p=self.payouts[x_chosen]) # agent learns of reward agent.reward = reward # agent updates parameters based on the data agent.update() self.total_reward += reward agent.collect_data() return self.total_reward

根据动作的数量，点以概率p进行二项分布（就像它们可以连续分布一样，本质不会改变）。 我还将定义BaseSampler类-仅用于存储日志和各种属性。

 class BaseSampler: def __init__(self, env, n_samples=None, n_learning=None, e=0.05): self.env = env self.shape = (env.n_k, n_samples) self.variants = env.variants self.n_trials = env.n_trials self.payouts = env.payouts self.ad_i = np.zeros(env.n_trials) self.r_i = np.zeros(env.n_trials) self.thetas = np.zeros(self.n_trials) self.regret_i = np.zeros(env.n_trials) self.thetaregret = np.zeros(self.n_trials) self.a = np.ones(env.n_k) self.b = np.ones(env.n_k) self.theta = np.zeros(env.n_k) self.data = None self.reward = 0 self.total_reward = 0 self.k = 0 self.i = 0 self.n_samples = n_samples self.n_learning = n_learning self.e = e self.ep = np.random.uniform(0, 1, size=env.n_trials) self.exploit = (1 - e) def collect_data(self): self.data = pd.DataFrame(dict(ad=self.ad_i, reward=self.r_i, regret=self.regret_i))

在下面，我们定义10个选项和每个选项的回报。 最好的选择是选项9，投资回报率为0.11％。

 variants = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] payouts = [0.023, 0.03, 0.029, 0.001, 0.05, 0.06, 0.0234, 0.035, 0.01, 0.11]

为了建立基础，我们还定义了RandomSampler类。 此类需要作为基线模型。 他只是在每次尝试时纯粹随机选择一个选项，而不会更新他的参数。

 class RandomSampler(BaseSampler): def __init__(self, env): super().__init__(env) def choose_k(self): self.k = np.random.choice(self.variants) return self.k def update(self): # nothing to update #self.thetaregret[self.i] = self.thetaregret[self.i] #self.regret_i[self.i] = np.max(self.thetaregret) - self.theta[self.k] #self.thetas[self.i] = self.theta[self.k] self.thetaregret[self.i] = np.max(self.theta) - self.theta[self.k] self.a[self.k] += self.reward self.b[self.k] += 1 self.theta = self.a/self.b self.ad_i[self.i] = self.k self.r_i[self.i] = self.reward self.i += 1

其他型号具有以下结构。 都具有choose_k和更新方法。 choice_k实现了代理选择选项的方法。 update更新代理的参数-此方法表征代理选择选项的能力如何变化（对于RandomSampler，此能力不会以任何方式改变）。 我们使用以下模式在环境中运行代理。


 en0 = Environment(machines, payouts, n_trials=10000) rs = RandomSampler(env=en0) en0.run(agent=rs)

epsilon-greedy算法的本质如下。

  1. 随机选择k次尝试n次。
  2. 在每次尝试中，针对每个选项，评估彩金。
  3. 经过n次尝试：
  4. 以概率1- e选择增益最高的k；
  5. 以概率e随机选择K。

Epsilon-贪婪代码：
 class eGreedy(BaseSampler): def __init__(self, env, n_learning, e): super().__init__(env, n_learning, e) def choose_k(self): # e% of the time take a random draw from machines # random k for n learning trials, then the machine with highest theta self.k = np.random.choice(self.variants) if self.i < self.n_learning else np.argmax(self.theta) # with 1 - e probability take a random sample (explore) otherwise exploit self.k = np.random.choice(self.variants) if self.ep[self.i] > self.exploit else self.k return self.k # every 100 trials update the successes # update the count of successes for the chosen machine def update(self): # update the probability of payout for each machine self.a[self.k] += self.reward self.b[self.k] += 1 self.theta = self.a/self.b #self.total_reward += self.reward #self.regret_i[self.i] = np.max(self.theta) - self.theta[self.k] #self.thetaregret[self.i] = self.thetaregret[self.i] self.thetas[self.i] = self.theta[self.k] self.thetaregret[self.i] = np.max(self.thetas) - self.theta[self.k] self.ad_i[self.i] = self.k self.r_i[self.i] = self.reward self.i += 1


在图表的下方，您可以看到纯随机抽样的结果，也就是说，这里没有模型。 该图显示了算法的每次选择（如果有1万次尝试）所做出的选择。 该算法仅尝试，但不学习。 他总共获得418分。


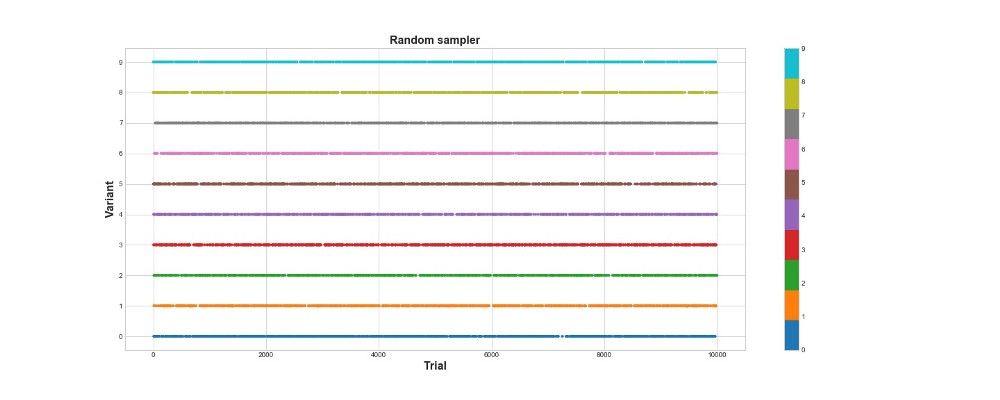
让我们看看epsilon-greedy算法在相同环境中的行为。 在e = 0.1和n_learning = 500的情况下运行该算法一万次（代理仅尝试前500次尝试，然后以e = 0.1的概率尝试）。 让我们根据它在环境中得分的总数来评估算法。


 en1 = Environment(machines, payouts, n_trials) eg = eGreedy(env=en1, n_learning=500, e=0.1) en1.run(agent=eg)


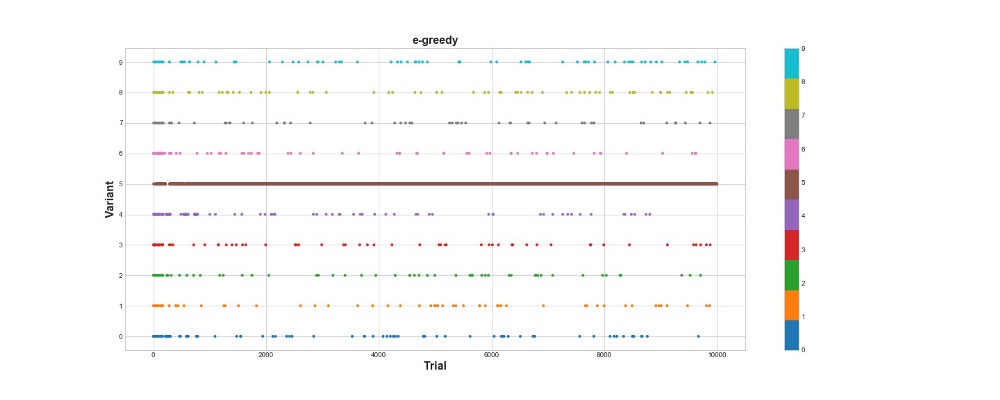
Epsilon-greedy算法获得788分，几乎是随机算法的2倍-超级！ 第二张图很好地说明了该算法。 我们看到，对于前500个步骤，动作近似均匀地分布，并且K是随机选择的。 但是，然后它开始大量利用选项5-这是一个非常强大的选项，但不是最佳选择。 我们还看到代理仍然随机选择10％的时间。


这非常酷-我们只写了几行代码，现在我们已经有了一个功能强大的算法，可以探索期权的空间并做出接近最佳的决策。 另一方面，该算法未找到最佳选择。 是的，我们可以增加学习的步骤数，但是这样一来，我们将在随机搜索上花费更多的时间，从而进一步恶化最终结果。 另外，默认情况下会将随机性缝入此过程-可能找不到最佳算法。


稍后，我将多次运行每种算法，以便我们可以相互比较它们。 但是现在，让我们看一下汤普森采样并在相同的环境中对其进行测试。


汤普森采样


汤普森采样与epsilon-greedy算法在本质上有三点不同：

  1. 这不是贪婪。
  2. 它以更复杂的方式进行尝试。
  3. 是贝叶斯。

要点是第3款，其后是第1和第2款。

该算法的本质是这样的：

  1. 将每个选项的投资回报率的初始Beta分布设置在0和1之间。
  2. 从此分布中采样选项，选择最大Theta参数。
  3. 选择与最大theta相关的选项k。
  4. 查看已计分的分数，更新分配参数。

在此处阅读有关beta分发的更多信息。
关于它在Python中的使用- 在这里 。

算法代码：

  class ThompsonSampler(BaseSampler): def __init__(self, env): super().__init__(env) def choose_k(self): # sample from posterior (this is the thompson sampling approach) # this leads to more exploration because machines with > uncertainty can then be selected as the machine self.theta = np.random.beta(self.a, self.b) # select machine with highest posterior p of payout self.k = self.variants[np.argmax(self.theta)] #self.k = np.argmax(self.a/(self.a + self.b)) return self.k def update(self): #update dist (a, b) = (a, b) + (r, 1 - r) self.a[self.k] += self.reward self.b[self.k] += 1 - self.reward # ie only increment b when it's a swing and a miss. 1 - 0 = 1, 1 - 1 = 0 #self.thetaregret[self.i] = self.thetaregret[self.i] #self.regret_i[self.i] = np.max(self.theta) - self.theta[self.k] self.thetas[self.i] = self.theta[self.k] self.thetaregret[self.i] = np.max(self.thetas) - self.theta[self.k] self.ad_i[self.i] = self.k self.r_i[self.i] = self.reward self.i += 1

该算法的形式符号如下所示。

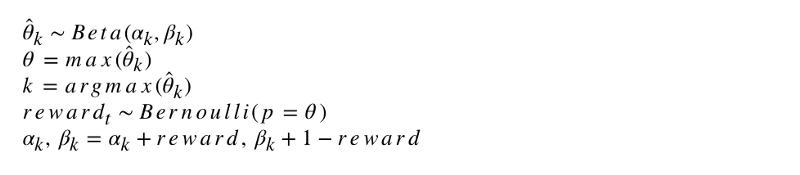
让我们对此算法进行编程。 像其他代理一样，ThompsonSampler继承自BaseSampler并定义了自己的select_k和update方法。 现在启动我们的新代理。


  en2 = Environment(machines, payouts, n_trials) tsa = ThompsonSampler(env=en2) en2.run(agent=tsa)


如您所见，他的得分高于epsilon-greedy算法。 太好了！ 让我们看一下尝试选择的图表。 可以看到两个有趣的东西。 首先，代理正确地发现了最佳选项（选项9）并充分利用了它。 其次，该代理使用了其他选项，但是以一种更棘手的方式-在尝试了1000次之后，该代理除了主要选项之外，还主要使用了其他选项中最强大的选项。 换句话说，他不是随机选择，而是更胜任。


为什么这样做？ 这很简单-每个选项的预期收益的后验分布的不确定性意味着，每个选项的选择概率大约与它的形状成正比，由alpha和beta参数确定。 换句话说，在每次尝试中，Thompson采样都会根据具有最大利益的后验概率触发期权。 粗略地说，代理从分布信息中获得有关不确定性的信息，然后决定何时检查环境以及何时使用该信息。 例如，具有较高后验不确定性的弱选择可能会为此尝试最多。 但是对于大多数尝试而言，其后验分布越强，其平均值越大，其标准偏差就越小，因此，选择它的机会就越大。


汤普森算法的另一个显着特性：由于它是贝叶斯算法，因此我们可以使用其参数来估计每个选项的投资回报估计中的不确定性。 下图显示了6个不同点的后验分布，并尝试了20,000次。 您会看到分配如何逐渐收敛到具有最佳回报的期权。



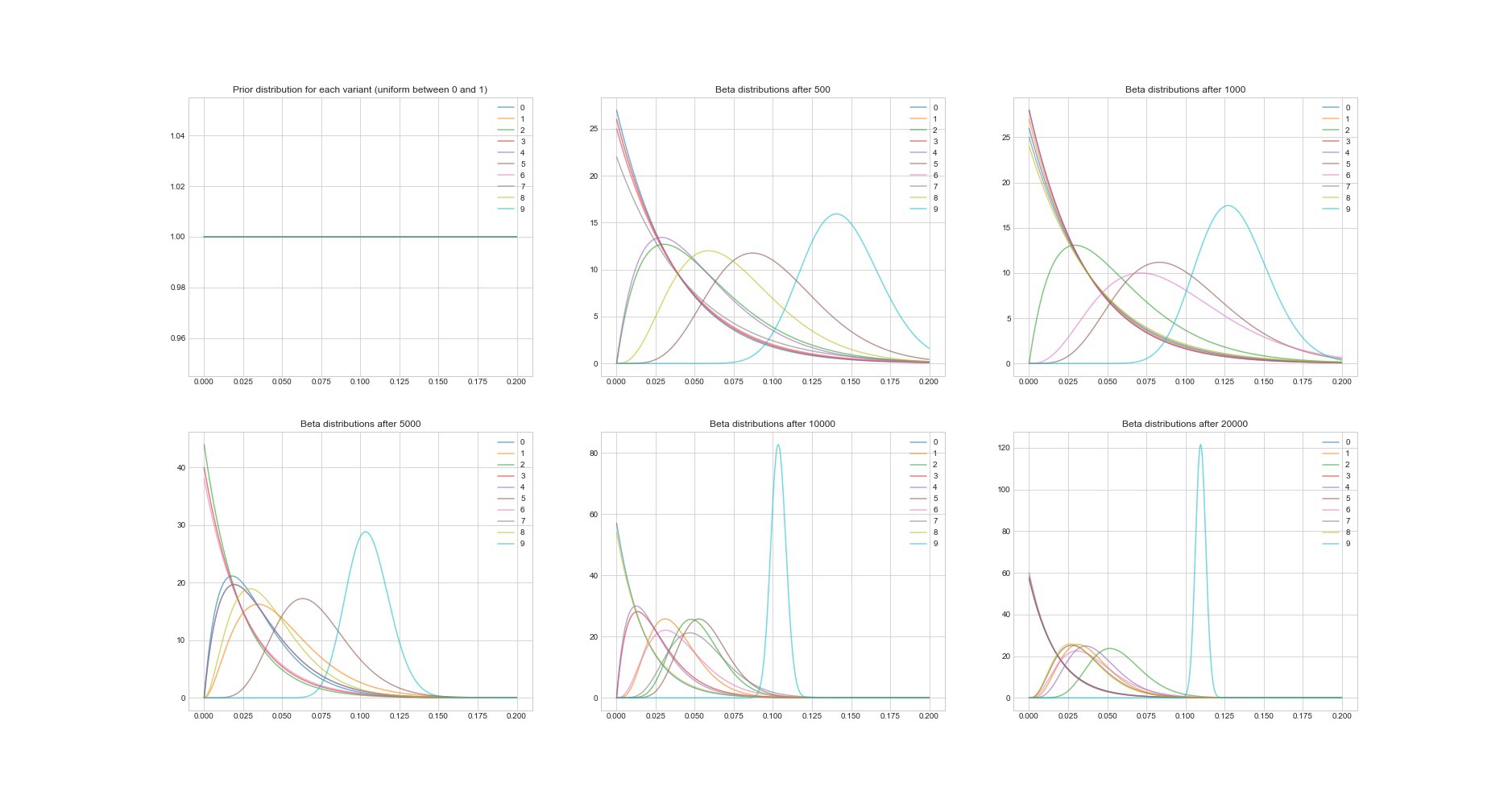
现在在100个模拟中比较所有3个代理。 1次模拟是一次10,000次尝试的代理启动。



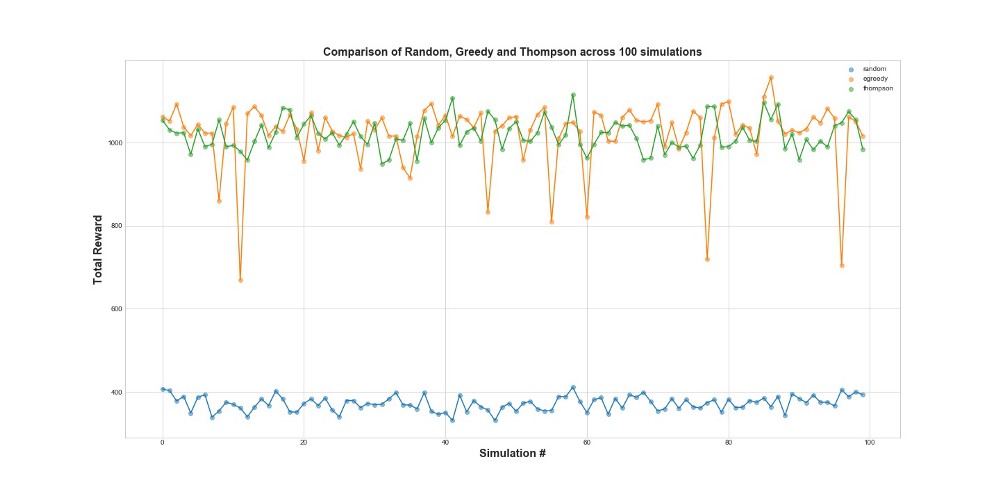
从图中可以看出，epsilon-greedy策略和Thompson采样都比随机采样要好得多。 您可能会惊讶于epsilon贪婪策略和Thompson采样在性能方面实际上是可比的。 Epsilon-greedy策略可能非常有效，但风险更高，因为它可能会卡在次优的选项上-从图中的失败中可以看出。 但是汤普森采样不能，因为它以更复杂的方式在选项空间中进行选择。


遗憾


评估算法效果的另一种方法是评估后悔。 粗略地说，相对于已经采取的行动，它越小越好。 下面是对错误的总遗憾和遗憾的图表。 再说一次-后悔越少越好。



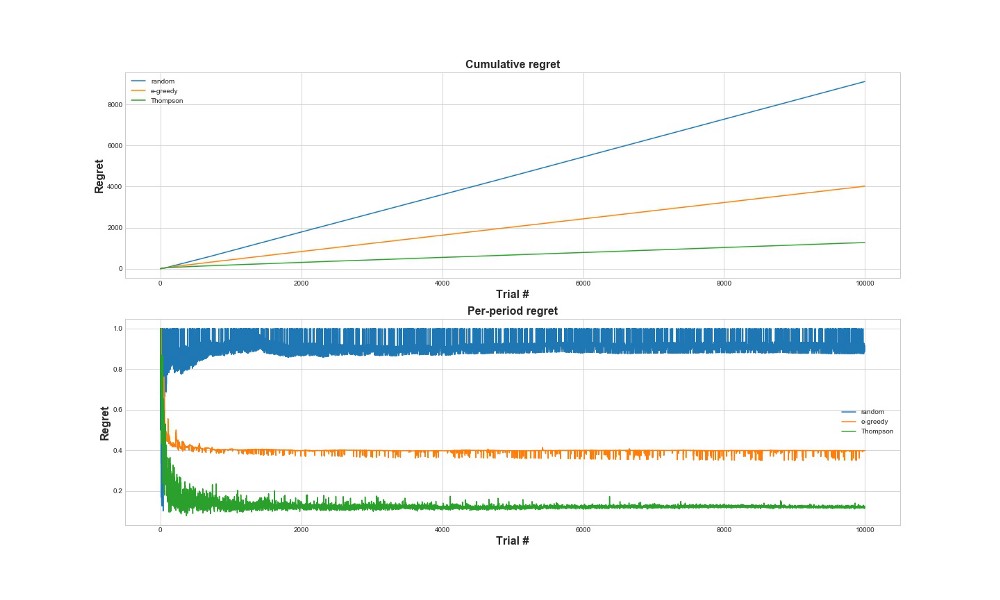
在上方的图表中，我们看到了总的遗憾，而在下方的图表中，我们看到了这次尝试。 从图中可以看出，汤普森采样收敛到最小后悔的速度比ε-贪婪策略快得多。 并且它收敛到一个较低的水平。 使用Thompson采样，代理可以减少后悔，因为他可以更好地检测最佳选项并更好地尝试最有前途的选项-因此Thompson采样特别适合于更高级的用例，例如用于选择k的统计模型或神经网络。


结论


这是一篇很长的技术文章。 总而言之，如果我们有很多要实时测试的选项，我们可以使用相当复杂的采样方法。 汤普森采样的一个很好的特点之一是它以一种相当棘手的方式平衡了使用和探索。 也就是说，我们可以让他实时优化解决方案选项的分配。 这些是很酷的算法，对于企业而言，它们应该比A / B测试更有用。


重要！ 汤普森采样并不意味着您不需要进行A / B测试。 通常，他们首先在他的帮助下找到最佳选择，然后对它们进行A / B测试。

Source: https://habr.com/ru/post/zh-CN425619/

More articles:


All Articles