◻️ 🏇🏿 😀 我们正在用Python做一个机器学习项目。第二部分 🤰 🧖🏾 🚀

Python的完整机器学习入门：第二部分

将机器学习项目的所有部分放在一起可能很棘手。在本系列文章中，我们将使用真实数据遍历机器学习过程实施的所有阶段，并找出各种技术如何相互结合。

在第一篇文章中，我们清理并整理了数据，进行了探索性分析，收集了一组可在模型中使用的属性，并设置了用于评估结果的基准。在本文的帮助下，我们将学习如何在Python中实现并比较几种机器学习模型，执行超参数优化以优化最佳模型，并在测试数据集上评估最终模型的性能。

所有项目代码都在GitHub上，这是与当前文章相关的第二个笔记本。您可以根据需要使用和修改代码！

模型评估与选择

备注：我们正在进行一项受控的回归任务，利用纽约建筑物的能源信息创建一个模型，该模型预测特定建筑物将获得的能源之星得分。我们对预测的准确性和模型的可解释性都感兴趣。

今天，您可以从许多可用的机器学习模型中进行选择，而这种丰富性可能会令人生畏。当然，网络上有比较的评论，可以帮助您选择算法时进行导航，但是我更喜欢尝试一些，看看哪种更好。在大多数情况下，机器学习基于经验而不是理论结果，因此几乎不可能事先了解哪种模型更准确。

通常建议您从简单的，可解释的模型开始，例如线性回归，如果结果不令人满意，则继续使用更复杂但通常更准确的方法。该图（非常反科学）显示了某些算法的准确性和可解释性之间的关系：

可解释性和准确性（来源）。

我们将评估五个复杂程度不同的模型：

线性回归。
k最近邻的方法。
“随机森林。”
梯度提升。
支持向量的方法。

我们将不考虑这些模型的理论装置，而是它们的实现。如果您对理论感兴趣，请查看《统计学习入门》（免费）或使用Scikit-Learn和TensorFlow进行动手机器学习。这两本书都很好地解释了该理论，并分别展示了在R和Python语言中使用上述方法的有效性。

填写缺失值

尽管清除数据时，我们丢弃了缺少一半以上值的列，但仍然有很多值。机器学习模型无法处理缺失的数据，因此我们需要对其进行填写。

首先，我们考虑数据并记住它们的外观：

import pandas as pd import numpy as np # Read in data into dataframes train_features = pd.read_csv('data/training_features.csv') test_features = pd.read_csv('data/testing_features.csv') train_labels = pd.read_csv('data/training_labels.csv') test_labels = pd.read_csv('data/testing_labels.csv') Training Feature Size: (6622, 64) Testing Feature Size: (2839, 64) Training Labels Size: (6622, 1) Testing Labels Size: (2839, 1)

每个NaN值都是数据中的缺失记录。您可以用不同的方式填充它们，我们将使用相当简单的中值插补方法，该方法将缺失的数据替换为对应列的平均值。

在下面的代码中，我们将使用中值策略创建一个Scikit-Learn Imputer Imputer 。然后，我们根据训练数据对其进行训练（使用imputer.fit ），并将其应用于填充训练和测试集中的缺失值（使用imputer.transform ）。也就是说， 测试数据中缺少的记录将用训练数据中的相应中值填充。

我们进行填充，并且不按原样对数据进行训练，以避免当来自测试数据集的信息进入训练时测试数据泄漏的问题。

 # Create an imputer object with a median filling strategy imputer = Imputer(strategy='median') # Train on the training features imputer.fit(train_features) # Transform both training data and testing data X = imputer.transform(train_features) X_test = imputer.transform(test_features) Missing values in training features: 0 Missing values in testing features: 0

现在所有值都已填满，没有缝隙了。

功能缩放

缩放是更改特征范围的一般过程。这是必要的步骤，因为符号以不同的单位进行测量，这意味着它们涵盖了不同的范围。这极大地扭曲了支持向量法和k最近邻法等算法的结果，这些算法考虑了测量之间的距离。通过缩放，您可以避免这种情况。尽管诸如线性回归和“随机森林”之类的方法不需要缩放特征，但比较几种算法时最好不要忽略此步骤。

我们将使用每个属性在0到1的范围内缩放。我们将属性的所有值取下来，选择最小值，然后将其除以最大值和最小值（范围）之差。这种缩放方法通常称为标准化，而另一种主要方法是标准化。

这个过程很容易手动实现，因此我们MinMaxScaler使用Scikit-Learn提供的MinMaxScaler对象。此方法的代码与用于填写缺失值的代码相同，仅使用缩放而不是粘贴。回想一下，我们仅在训练集上学习模型，然后转换所有数据。

 # Create the scaler object with a range of 0-1 scaler = MinMaxScaler(feature_range=(0, 1)) # Fit on the training data scaler.fit(X) # Transform both the training and testing data X = scaler.transform(X) X_test = scaler.transform(X_test)

现在，每个属性的最小值为0，最大值为1。填充缺失值和属性的缩放-几乎所有机器学习过程都需要这两个阶段。

我们在Scikit-Learn中实现机器学习模型

经过所有准备工作，创建，训练和运行模型的过程相对简单。我们将使用Python中的Scikit-Learn库，该库的文档精美，并具有用于构建模型的复杂语法。通过学习如何在Scikit-Learn中创建模型，您可以快速实现各种算法。

我们将说明使用梯度提升的创建，训练（ .fit ）和测试（ .fit ）的过程：

 from sklearn.ensemble import GradientBoostingRegressor # Create the model gradient_boosted = GradientBoostingRegressor() # Fit the model on the training data gradient_boosted.fit(X, y) # Make predictions on the test data predictions = gradient_boosted.predict(X_test) # Evaluate the model mae = np.mean(abs(predictions - y_test)) print('Gradient Boosted Performance on the test set: MAE = %0.4f' % mae) Gradient Boosted Performance on the test set: MAE = 10.0132

只需一行代码即可进行创建，培训和测试。要构建其他模型，我们使用相同的语法，仅更改算法的名称。

为了客观地评估模型，我们使用目标的中值计算了基准水平，得出24.5。而且结果要好得多，因此可以使用机器学习来解决我们的问题。

在我们的案例中，梯度提升（MAE = 10.013）稍好于“随机森林”（10.014 MAE）。尽管不能完全相信这些结果，但是对于超参数，我们大多使用默认值。模型的有效性在很大程度上取决于这些设置，尤其是在支持向量方法中。但是，基于这些结果，我们将选择梯度增强并开始对其进行优化。

超参数模型优化

选择模型后，您可以通过调整超参数来针对要解决的任务对其进行优化。

但是首先，让我们了解什么是超参数以及它们与普通参数有何不同？

可以将模型的超参数视为算法的设置，这是我们在训练开始之前设置的。例如，超参数是“随机森林”中的树数，或k近邻法中的邻居数。
模型参数-她在训练期间学到的东西，例如线性回归中的权重。

通过控制超参数，我们影响了模型的结果，改变了模型的不足和再训练之间的平衡。在学习中，情况是该模型不够复杂（自由度太小），无法研究符号和目标的对应关系。训练不足的模型具有较高的偏差，可以通过使模型复杂化来进行校正。

再训练是一种情况，模型实际上会记住训练数据。重新训练的模型具有很高的方差，可以通过正则化限制模型的复杂性来进行调整。训练不足的模型和再训练的模型都无法很好地概括测试数据。

选择正确的超参数的困难在于，对于每个任务，将有一个唯一的最佳集合。因此，选择最佳设置的唯一方法是对新数据集尝试不同的组合。幸运的是，Scikit-Learn有许多方法可以使您有效地评估超参数。此外，诸如TPOT之类的项目正在尝试使用诸如遗传编程之类的方法来优化对超参数的搜索。在本文中，我们仅限于使用Scikit-Learn。

交叉检查随机搜索

让我们实现一种称为随机交叉验证查找的超参数调整方法：

随机搜索 -一种选择超参数的技术。我们定义了一个网格，然后从网格中随机选择各种组合，这与网格搜索相反，在网格搜索中，我们先后尝试每种组合。顺便说一句，随机搜索的效果几乎与网格搜索一样好，但是速度更快。
交叉检查是评估所选超参数组合的一种方式。与其将数据分为训练集和测试集（这减少了可用于训练的数据量），我们将使用k块交叉验证（K折叠交叉验证）。为此，我们将训练数据划分为k个块，然后运行迭代过程，在此过程中，我们首先在k-1个块上训练模型，然后在第k个块上学习时比较结果。我们将重复该过程k次，最后将获得每次迭代的平均误差值。这将是最终评估。

这是k = 5时k块交叉验证的图形说明：

整个交叉验证随机搜索过程如下所示：

我们设置了一个超参数网格。
随机选择超参数的组合。
使用此组合创建模型。
我们使用k块交叉验证来评估模型的结果。
我们决定哪些超参数给出最佳结果。

当然，这不是手动完成的，而是使用Scikit-Learn提供的RandomizedSearchCV ！

小题外话：梯度增强方法

我们将使用基于梯度增强的回归模型。这是一种集体方法，也就是说，该模型由众多“弱学习者”组成，在这种情况下，它们来自单独的决策树。如果学生以“随机森林”之类的并行算法学习，然后通过投票选择预测结果，那么在以梯度增强之类的增强算法中，学生将按顺序学习，并且每个人都“专注于”其前辈所犯的错误。

近年来，增强算法变得很流行，并且经常在机器学习竞赛中获胜。梯度提升是其中使用梯度下降来最大程度降低功能成本的一种实现方式。在Scikit-Learn中，梯度提升的实现不如在其他库中（例如，在XGBoost中）有效，但是在小型数据集上效果很好，并且给出了相当准确的预测。

返回超参数设置

在使用梯度提升的回归中，有许多超参数需要配置，有关详细信息，请参考Scikit-Learn文档。我们将优化：

loss ：损失函数的最小化；
n_estimators ：使用的弱决策树的数量（决策树）；
max_depth ：每个决策树的最大深度；
min_samples_leaf ：决策树的叶子节点中应包含的最少示例数；
min_samples_split ：拆分决策树节点所需的最少示例数；
max_features ：用于分隔节点的最大功能数。

不知道是否有人真的了解这一切如何工作，而找到最佳组合的唯一方法是尝试不同的选择。

在此代码中，我们创建一个超参数网格，然后创建一个RandomizedSearchCV对象，并使用4块交叉验证搜索25个不同的超参数组合：

 # Loss function to be optimized loss = ['ls', 'lad', 'huber'] # Number of trees used in the boosting process n_estimators = [100, 500, 900, 1100, 1500] # Maximum depth of each tree max_depth = [2, 3, 5, 10, 15] # Minimum number of samples per leaf min_samples_leaf = [1, 2, 4, 6, 8] # Minimum number of samples to split a node min_samples_split = [2, 4, 6, 10] # Maximum number of features to consider for making splits max_features = ['auto', 'sqrt', 'log2', None] # Define the grid of hyperparameters to search hyperparameter_grid = {'loss': loss, 'n_estimators': n_estimators, 'max_depth': max_depth, 'min_samples_leaf': min_samples_leaf, 'min_samples_split': min_samples_split, 'max_features': max_features} # Create the model to use for hyperparameter tuning model = GradientBoostingRegressor(random_state = 42) # Set up the random search with 4-fold cross validation random_cv = RandomizedSearchCV(estimator=model, param_distributions=hyperparameter_grid, cv=4, n_iter=25, scoring = 'neg_mean_absolute_error', n_jobs = -1, verbose = 1, return_train_score = True, random_state=42) # Fit on the training data random_cv.fit(X, y) After performing the search, we can inspect the RandomizedSearchCV object to find the best model: # Find the best combination of settings random_cv.best_estimator_ GradientBoostingRegressor(loss='lad', max_depth=5, max_features=None, min_samples_leaf=6, min_samples_split=6, n_estimators=500)

您可以通过选择接近这些最佳值的网格参数来将这些结果用于网格搜索。但是进一步调整不太可能显着改善模型。有一个一般规则：特征的有效构造将比最昂贵的超参数设置对模型的准确性产生更大的影响。这是与机器学习有关的获利能力下降的定律：设计属性提供最高的回报，而超参数调整仅带来适度的好处。

要在保留其他超参数值的同时更改估计量（决策树）的数量，可以执行一个实验来证明此设置的作用。这里给出了实现，但是结果如下：

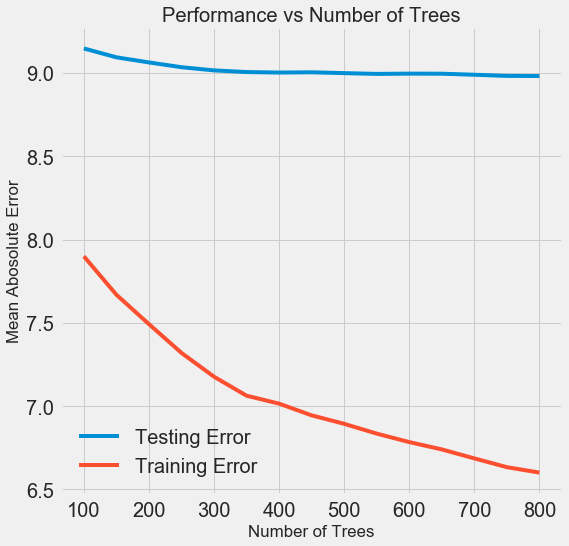
随着模型使用的树木数量增加，训练和测试期间的错误级别降低。但是学习错误的减少速度要快得多，因此，该模型被重新训练：在训练数据上显示出优异的结果，但在测试数据上却表现得较差。

在测试数据上，准确性始终会下降（因为模型看到了针对训练数据集的正确答案），但是下降幅度很大则表明了重新训练。可以通过增加训练数据量或使用超参数降低模型的复杂性来解决此问题。这里我们不会涉及超参数，但是我建议您始终注意重新训练的问题。

对于我们的最终模型，我们将使用800位评估者，因为这将使我们在交叉验证中的错误级别最低。现在测试模型！

使用测试数据进行评估

作为负责人，我们确保在培训期间我们的模型绝不会获得对测试数据的访问。因此，当将测试数据用于实际任务时，我们可以将准确性用作模型质量指标。

我们提供模型测试数据并计算误差。这是默认梯度提升算法和我们自定义模型的结果的比较：

 # Make predictions on the test set using default and final model default_pred = default_model.predict(X_test) final_pred = final_model.predict(X_test) Default model performance on the test set: MAE = 10.0118. Final model performance on the test set: MAE = 9.0446.

超参数调整有助于将模型准确性提高约10％。根据情况，这可能是非常重要的改进，但是需要很多时间。

您可以使用Jupyter Notebooks中的magic %timeit比较两种模型的训练时间。首先，测量模型的默认持续时间：

 %%timeit -n 1 -r 5 default_model.fit(X, y) 1.09 s ± 153 ms per loop (mean ± std. dev. of 5 runs, 1 loop each)

一秒钟的学习非常不错。但是调整后的模型并不是那么快：

 %%timeit -n 1 -r 5 final_model.fit(X, y) 12.1 s ± 1.33 s per loop (mean ± std. dev. of 5 runs, 1 loop each)

这种情况说明了机器学习的基本方面：都是关于妥协。始终需要在精度和可解释性之间，位移与分散之间，精度与操作时间之间等等之间进行权衡。正确的组合完全取决于特定的任务。在我们的案例中，相对而言，工作时间增加12倍是很大的，但从绝对角度而言，这是微不足道的。

我们得到了最终的预测结果，现在让我们对其进行分析，找出是否存在明显的偏差。左边是预测值和实际值的密度图，右边是误差的直方图：

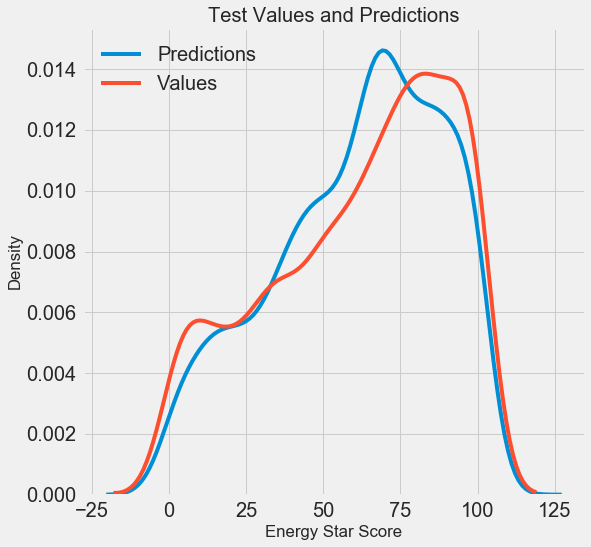
模型的预测可以很好地重复实际值的分布，而在训练数据上，密度峰值的位置更接近中值（66），而不是真实密度峰值（大约100）。误差几乎呈正态分布，尽管当模型预测与实际数据有很大差异时，误差有几个较大的负值。在下一篇文章中，我们将仔细研究结果的解释。

结论

在本文中，我们研究了解决机器学习问题的几个阶段：

填写缺失值和缩放功能。
评估和比较几种模型的结果。
使用随机网格搜索和交叉验证进行超参数调整。
使用测试数据评估最佳模型。

结果表明，我们可以根据可用的统计数据，使用机器学习来预测能源之星得分。借助梯度提升，测试数据的误差为9.1。超参数调整可以极大地改善结果，但要以明显降低速度为代价。这是机器学习中要考虑的众多折衷之一。

在下一篇文章中，我们将尝试弄清楚我们的模型是如何工作的。我们还将研究影响能源之星评分的主要因素。如果我们知道该模型是准确的，那么我们将尝试理解为什么它以此方式进行预测以及这可以告诉我们有关问题本身的信息。

我们正在用Python做一个机器学习项目。 第二部分