
我们继续熟悉非常年轻但又非常漂亮和强大的编程语言Julia 。 六年的Beta版终于结束了,因此现在您不必担心语法更改。 虽然每个人都在争论从一个索引开始是好是坏,但躁动不安的社区正在四处乱窜:新图书馆问世,旧图书馆正在更新,严肃的项目正在启动,学生们正在大学积极教授这种语言。 因此,不要让我们落后! 我们使茶变得更强壮,因为我们将在今晚编写代码!
准备工作
这里有俄文的小篇幅评论,在集线器上也有对语言和安装说明的了解 。 同样,着重于对Windows Management Framework的需求 ,下载软件包会遇到问题。
升级后, JuliaPRO现在仅包含Juno 。 但是我个人更喜欢Jupyter :笔记本电脑上没有问题,而且它在浏览器中工作并立即创建便笺和公式非常方便,通常是创建报告,幻灯片或手册的理想选择。
Julia有几个软件包,其中最成功的软件包作为后端包含在Plot中。 Plots.jl语言:即各种图表库的接口。 因此, Plots.jl实际上只是解释您的命令,然后使用某种图形库创建图形。 这些背景图形库称为后端。 最好的部分是,您可以将许多不同的图形库与Plots.jl语法一起使用,并且我们还将看到Plots.jl为每个库都添加了新功能!
安装图形包要安装软件包,请在REPL,Juno或Jupyter中运行命令:
# Pkg.add("Plots") # 0.7.0 julia>] pkg>add Plots pkg>add GR pkg>add PyPlot pkg>add Gadfly pkg>add PlotlyJS pkg>add UnicodePlots
不必安装所有软件包,但是您应该知道每个软件包都有自己的特点 。 我更喜欢plotlyjs() :尽管速度没有差别,但它是非常互动的。 有一个缩放功能,可以沿平面移动,还可以保存文件,如果将Jupyter文档另存为html,则将保存所有功能。 因此,您可以添加到网站或进行交互式演示。 页面上的更多信息: 情节 , 牛d
无休止的素数模式
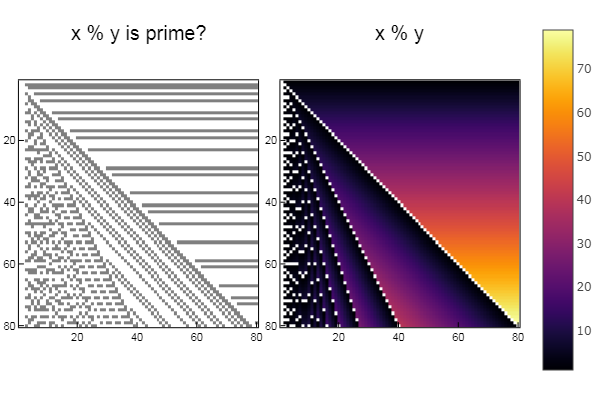
实施了有关Habr的文章的想法。 简而言之:如果我们获取该点的坐标并在横坐标和纵坐标之间使用一个运算(例如XOR或按位与) ,然后检查该数字的简单性或属于斐波那契数字,如果答案是肯定的,则用一种颜色填充该点,另一个是负面的? 检查:
操作百分比 using Plots plotlyjs() function eratosphen(n, lst) # ar = [i for i=1:n] ar[1] = 0 for i = 1:n if ar[i] != 0 push!(lst, ar[i]) for j = i:i:n ar[j] = 0 end end end end ertsfn = [] eratosphen(1000, ertsfn) # print(ertsfn) # print( size(ertsfn) ) # -> 168 N = 80 M = 80 W1 = [in( x % y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x % y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x % y is prime?") p2 = spy(W2, title = "x % y") plot(p1, p2, layout=(2),legend=false)
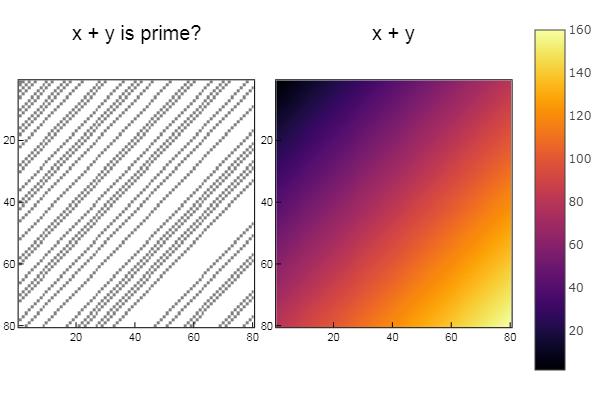
用于操作+ W1 = [in( x + y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x + y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x + y is prime?") p2 = spy(W2, title = "x + y") plot(p1, p2, layout=(2),legend=false)
操作| W1 = [in( x | y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x | y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x | y is prime?") p2 = spy(W2, title = "x | y") plot(p1, p2, layout=(2),legend=false)

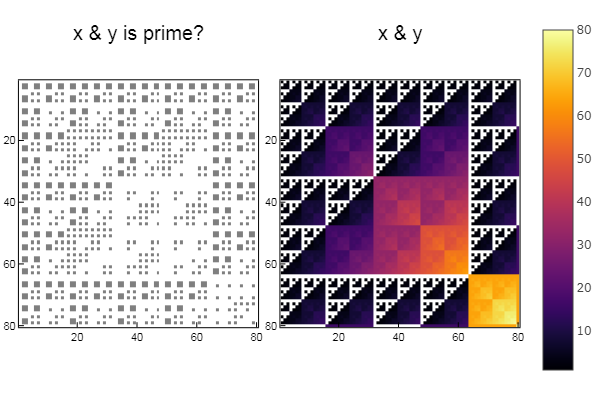
操作与 W1 = [in( x & y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x & y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x & y is prime?") p2 = spy(W2, title = "x & y") plot(p1, p2, layout=(2),legend=false)
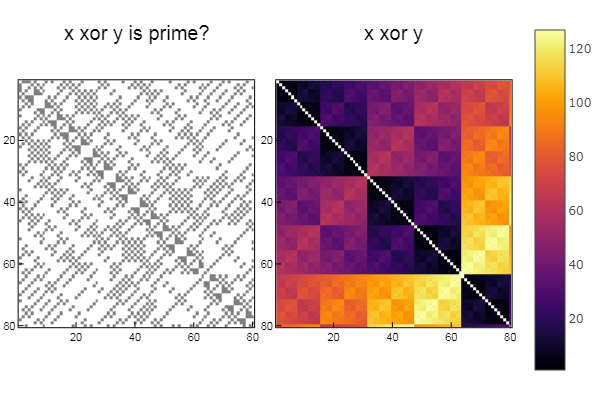
对于异或运算 W1 = [in( xor(x, y), ertsfn) for x = 1:N, y = 1:M]; W2 = [xor(x, y) for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x xor y is prime?") p2 = spy(W2, title = "x xor y") plot(p1, p2, layout=(2),legend=false)
现在一切都一样,但斐波那契数您可以像往常一样制作系列,例如:
function fib(n) a = 0 b = 1 for i = 1:n a, b = b, a + b end return a end fbncc = fib.( [i for i=1:10] )
但是,让我们使用矩阵表示( 更详细地说明 ):
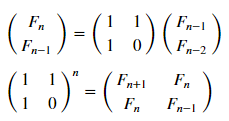
matr_fib = n -> [1 1; 1 0]^(n-1) # , n-1 mfbnc = [ matr_fib( i )[1,1] for i=1:17]; # 1,1 n- N = 100 M = N W1 = [in( x % y, mfbnc) for x = 1:N, y = 1:M]; W2 = [in( x | y, mfbnc) for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x % y ∈ fibonacci?") p2 = spy(W2, title = "x | y ∈ fibonacci?") plot(p1, p2, layout=(2),legend=false)
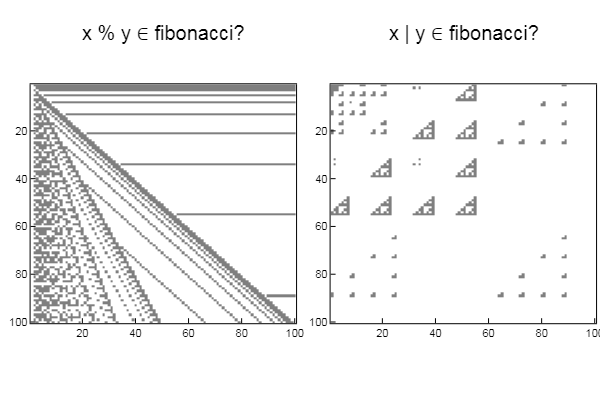
W1 = [in( xor(x, y), mfbnc) for x = 1:N, y = 1:M]; W2 = [in( x & y, mfbnc) for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x xor y ∈ fibonacci?") p2 = spy(W2, title = "x & y ∈ fibonacci?") plot(p1, p2, layout=(2),legend=false)
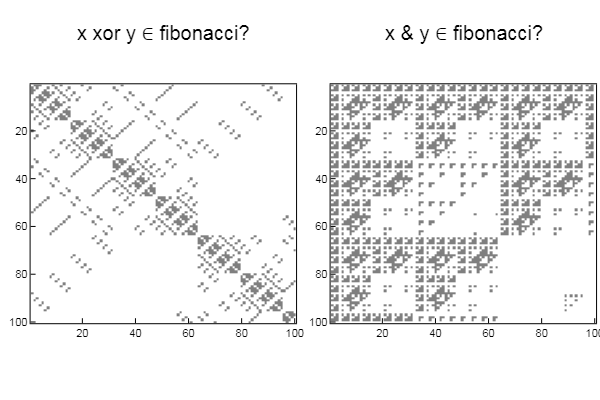
人物反映比较直
此类显示由矩阵确定:
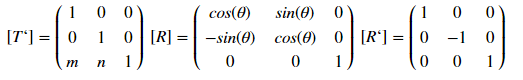
其中[T'],[R]和[R']分别是位移,旋转和反射矩阵。 如何运作? 让我们分析一个偏移量的示例。对于一个坐标为(x,y)的点,游戏中m乘x以及n的偏移将由以下转换确定:
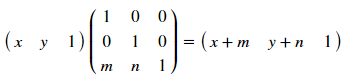
这些矩阵允许对各种多边形进行转换,主要是要记录彼此之间的坐标,而不要忘记最后的单位列。 因此[T]:
- 沿原点移动线以及要转换的多边形
- 旋转使其与X轴重合
- 反映多边形相对于X的所有点
- 然后反向旋转和转移
该主题在Rogers D.,Adams J.《计算机图形学的数学基础 》一书中有更详细的描述。
现在进行编码!
using Plots plotlyjs() f = x -> 0.4x + 2 # # X = [2 4 2 2]' Y = [4 6 6 4]' xs = [-2; 7] # ys = f(xs) inptmtrx = [ XY ones( size(X, 1), 1 ) ] # m = 0 n = -f(0) # Y displacement = [1 0 0; 0 1 0; mn 1] a = (ys[2]-ys[1]) / (xs[2]-xs[1]) # θ = -atan(a) rotation = [cos(θ) sin(θ) 0; -sin(θ) cos(θ) 0; 0 0 1] reflection = [1 0 0; 0 -1 0; 0 0 1] T = displacement * rotation * reflection * rotation^(-1) * displacement^(-1) # outptmtrx = inptmtrx * T plot( X, Y) plot!( xs, ys ) plot!( outptmtrx[:,1], outptmtrx[:,2] )
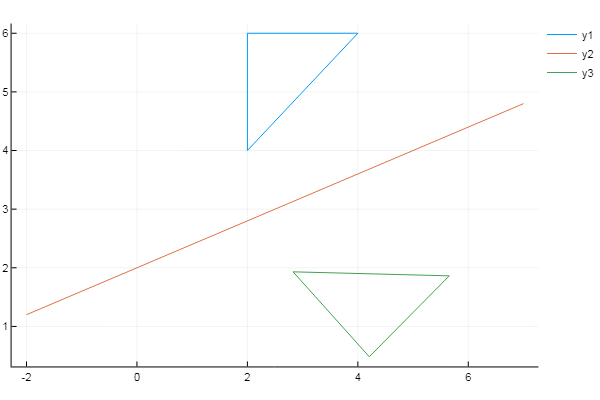
有趣的事实:如果您摆脱了希腊字符,而将第一行替换为
function y=f(x,t) y=0.4*x + 2 endfunction,
由于方括号[]将()上的数组的索引作为框架,将图上的筏plot( X, Y, xs, ys, trianglenew(:,1), trianglenew(:,2) )构成框架,因此此代码已在Scilab中启动。
处理三维图形
其中一些软件包支持三维图形的构建。 但是,我想单独提及Makie相当强大的可视化工具 ,该工具可以与在julia 中实现OpenGL功能的GLFW和GLAbstraction软件包一起使用。 有关Makie的更多信息。 我们掩盖了他的赞同
扰流板 using Makie N = 51 x = linspace(-2, 2, N) y = x z = (-x .* exp.(-x .^ 2 .- (y') .^ 2)) .* 4 scene = wireframe(x, y, z) xm, ym, zm = minimum(scene.limits[]) scene = surface!(scene, x, y, z) contour!(scene, x, y, z, levels = 15, linewidth = 2, transformation = (:xy, zm)) scene
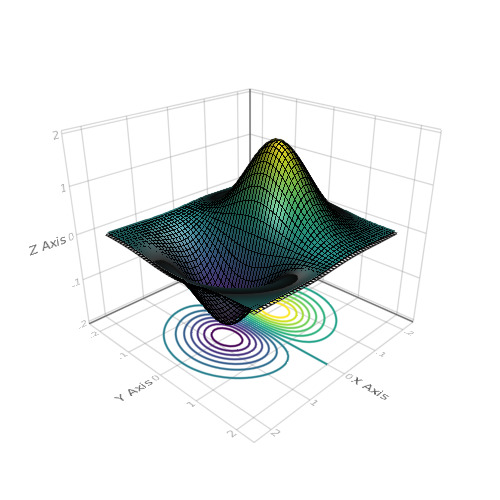
wireframe(Makie.loadasset("cat.obj"))

using FileIO scene = Scene(resolution = (500, 500)) catmesh = FileIO.load(Makie.assetpath("cat.obj"), GLNormalUVMesh) mesh(catmesh, color = Makie.loadasset("diffusemap.tga"))

x = Makie.loadasset("cat.obj") mesh(x, color = :black) pos = map(x.vertices, x.normals) do p, n p => p .+ (normalize(n) .* 0.05f0) end linesegments!(pos, color = :blue)
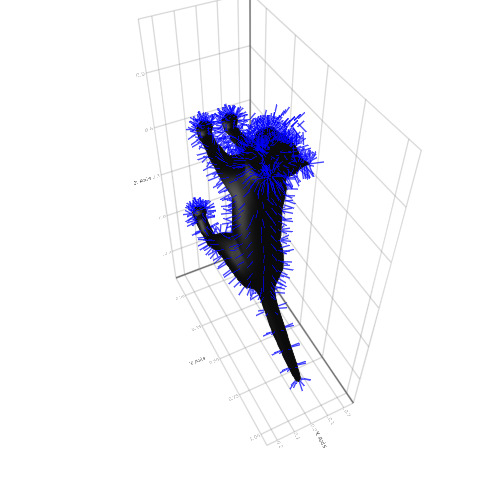
这就是图形。 交互性,动画,3D,大数据或简单图形的快速构建-不断发展的软件包将满足几乎任何口味和需求,此外,所有内容都非常易于学习。 随时下载实践练习并继续理解Julia!
UPD:以上所有清单都是在Jupyter中进行的,Julia为0.6.4。 不幸的是,Plots元软件包的某些功能已被删除或重命名,因此我们继续监视更新,但目前间谍已被完全替换:
julia> using GR julia> Z = [x | y for x = 1:40, y = 1:40]; julia> heatmap(Z)