旋转螺旋：数学和幻觉

当试图想象由麻醉物质引起的幻觉时，会想到旋涡，螺旋迷幻形式，立即类似于隧道视觉 。 但是这种几何结构不仅会引起迷幻药，例如LSD，大麻或可卡因碱 。 人们谈到在死亡时这种视力的发生，在癫痫和精神分裂症这样的痛苦情况下，由于感觉剥夺的结果，甚至是对眼球的简单压迫。 这种几何幻觉是如此普遍，以至于在上个世纪，科学家开始怀疑他们是否可以告诉我们有关大脑结构的一些基本知识。 而且，显然是。


在计算机上创建的表单常量。 前两个图像模拟接收LSD后发生的漏斗和螺旋。 左下角是大麻产生的蜂窝。 右下角是网络。

系统的几何幻觉最初是在1920年代由美国-德国心理学家Heinrich Kluver研究的 。 克鲁夫对视觉感知的兴趣最终使他尝试了由卡洛斯·卡斯塔内达 （ Carlos Castaneda）庆祝的仙人掌-仙人掌，他的精神活性成分麦斯卡琳在许多中美洲部落的萨满教法中发挥了重要作用。 墨斯卡林因引起幻觉而闻名。 Kluver在实验室中与助手一起使用pyeote，注意到在由甲斯卡林引起的幻觉中重复出现了几何形状，并将其分为四种类型，称它们为常数 ：隧道和漏斗，螺旋形，格子（包括蜂窝和三角形）和蜘蛛网。

在1970年代，数学家Jack Cowan和Bard Ermentraut使用Kluver的分类法创建了一个理论，该理论描述了当使我们相信我们看到几何图案时大脑中发生的事情。 他们的理论得到了其他科学家的进一步发展，包括最近成立的牛津合作应用数学中心数学和计算神经生物学教授保罗·布雷斯洛夫。

大脑皮层的条带在哪里*

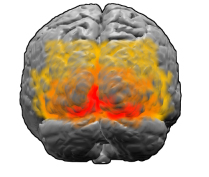视觉皮层。 红色标记区域V1

[ *参考越南童话故事“老虎从地带走到哪里” /大约。 佩雷夫 ]

处理人和哺乳动物图像的大脑视觉皮层的第一个区域是称为V1的区域。 实验证据（例如fMRI图像）表明Kluver模式也主要来自V1，并且在以后的视觉系统中不会出现。 像大脑的其他部分一样，V1具有复杂的，起皱的，折叠的结构-但是，有一种出奇的简单方法将我们在视野中看到的内容转换为V1中神经元的活动。 “想象一下我们正在部署V1，” Breslov说。 -可以想象成几毫米厚的神经组织，其中有许多层神经元。 初步近似，整个皮质深度的神经元的行为都类似，因此，如果将它们展平，则可以将V1想象成一个二维薄片。

视觉世界的对象或场景以二维图像的形式投影到每只眼睛的视网膜上，因此我们所看到的也可以看作是平板：视野。 可以通过两个坐标来指定此图纸上的每个点，例如地图上的点或平面模型V1上的点。 构成几何幻觉的明暗区域交替是由V1中神经元活动的高低交替区域引起的-神经元很快被激活的区域，反之亦然。

为了将视觉模式转换为神经元活动，必须使用坐标网格-根据该规则，视场的每个点都与平面模型V1的点相连。 1970年代，包括Cowen在内的科学家基于对视网膜神经元与V1中神经元相互作用的解剖结构的了解，制作了这样的网格。 对于视野的每个亮或暗部分，映射都定义了V1中神经元活动高或低的部分。

视网膜和皮质的这种成像如何改变克鲁弗的几何图案？ 事实证明，幻觉导致从中心发出的螺旋，圆形和射线，对应于V1中以给定角度通过的神经元活动带。 格子（例如蜂窝或单元格）对应于V1中的六边形活动模式。 这本身可能并不那么有趣，但是有一个先例：科学家在对图案形成的其他示例进行建模时观察到的是条带和六边形，例如液体的对流，或者更令人惊讶的是在动物皮肤上出现了斑点和条带。 控制这些图案形成的数学是众所周知的，并且还提出了一种对视觉皮层功能进行建模的机制。

从视野到视觉皮层

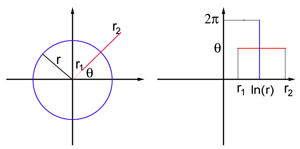
想象一下具有极坐标的平板形式的视场：每个点P由两个数字（r，θ）定义，其中r是到原点的距离，θ是线段OP和x轴之间的角度。 参考点对应于视场的中心。 V1也被建模为平板，但是这次具有笛卡尔坐标（x，y）。 对于本文而言，视场和平面模型V1的精确坐标显示太复杂了，但是对于离视场中心足够远的点（即，对于足够大的r），它类似于对数映射：

$$

$$x = \ ln {r} \\ y = \ theta$$

该映射将视场中半径为r的圆转换为x = ln r的直线垂直段，并将来自坐标O的原点以角度θ的光线转换为y =θ的直线水平段

豹斑在哪里

形成动物皮肤图案的第一个模型可以追溯到Alan Turing ，他以现代计算机科学之父而闻名，是来自Bletchley Park的黑客，他破解了代码。 Turing感兴趣的是空间均匀的系统（例如动物的胚胎的均匀细胞球）如何创建空间不均匀但静态的图案（例如斑马条纹）。

图灵认为，这些模式是反应扩散过程的结果 。 想象一下一个动物胚胎，其皮肤中存在两种化学物质。 其中一种是抑制自身和另一种化学物质产生的抑制剂。 另一种是引起两种物质产生的催化剂。

在图灵模型的初始时刻，两种化学物质理想地相互平衡-它们处于平衡状态，并且它们在胚胎上不同点的浓度不会随时间变化。 现在想象一下，由于某种原因，催化剂的浓度有一点增加。 这种轻微的干扰使整个系统运转。 催化剂局部浓度的增加意味着在那里产生更多的催化剂和抑制剂。 但是，这两种化合物还扩散到胚胎的皮肤上，在其他地方抑制和催化它们的产生。

例如，如果抑制剂的扩散速度快于催化剂，则它将迅速围绕扰动点并降低扰动点的浓度。 结果，我们得到了一个高浓度催化剂的区域，被高浓度的抑制剂包围着，换句话说，在抑制剂的背景上有一个催化剂点。 根据这两种化合物的扩散速度，可能在整个胚胎皮肤上出现这种斑点图案，并最终使其稳定。

图林（Thuring）写下了描述两种化合物之间竞争关系的微分方程组-您可以让它们及时发展，看看是否出现模式。 这些方程式取决于描述两种化合物扩散速率的参数：如果正确选择它们，则系统最终会稳定下来，形成可以通过更改参数而改变的特定模式。 该链接提供了Java中的applet ，您可以在其中试用参数并查看生成的模式。

动物形态方程

为了简单起见，想象一维线形式的胚胎。 在胚胎的任何时间t和x处，催化剂（活化剂）和抑制剂（抑制剂）的浓度由函数A（x，t）和I（x，t）确定。 它们根据以下规则随时间变化：

$$

$$\ frac {\部分A} {\部分t} = f（A，I）+ \ frac {\部分^ 2 A} {\部分x ^ 2} \\ \ frac {\部分I} {\部分t } = g（A，I）+ d \ frac {\部分^ 2 I} {\部分x ^ 2}$$

每个方程式右边的第一项描述了催化剂和抑制剂的产生量。 它们是催化剂和抑制剂浓度的函数，因为两者都会影响反应速率。

每个方程式右边的第二项是二阶导数，它描述了催化剂和抑制剂的梯度变化率。 他们设定扩散率。

第二个方程式右侧的附加项d是扩散系数，它表示抑制剂比催化剂扩散得快多少。 图灵表明，抑制剂速度的优越性是污渍产生的关键参数。

脑型

大脑中神经元的活动不是反应扩散过程，但是它与图灵模型类似。 Breslov说：“神经元通过称为轴突的数据输出通道相互发送信号。” 神经元对彼此的信号做出反应，这就是反应。 “与图案形成过程相比，信号传播如此之快，以至于它们可能被误认为是即时交互。” 因此，我们没有远距离的扩散，而是局部的过程。 催化剂和抑制剂的作用由两种不同类型的神经元发挥。 布雷斯洛夫说：“存在兴奋性神经元，这增加了其他神经元活跃的可能性，而抑制性神经元则降低了这种可能性。” “两类神经元之间的竞争类似于图灵模型中的催化剂-抑制剂机制。”


通过数学模型生成的V1中神经活动的条纹，六角形和矩形模式

受图灵过程的类比启发，Cowan和Ermentraut使用由Cowan和Hugh Wilson公式化的一组方程，创建了V1神经活动模型。 尽管方程式比图灵的方程式复杂得多，但您仍然可以玩同样的游戏，让系统随着时间的推移而发展，并观察神经活动模式是否发展。 布雷斯洛夫说：“您会发现，在某些条件下，如果增加参数（例如代表药物对皮层的影响），则会导致周期性模式的增长。”

Cowan and Ermentraut模型表明，几何幻觉是由V1的不稳定性引起的：例如，某种药物的存在使神经网络脱离了平衡状态，从而开始了刺激和抑制神经元之间相互作用的滚雪球式生长过程，然后稳定了该过程。以V1中神经活动的条纹或六角形形式出现。 然后，我们以Kluver在视野中描述的几何结构形式“观察”这种模式。

大脑中的对称性

实际上，一切都不像Cowan和Ermentraut模型中的那么简单，因为神经元不仅对亮和暗的图像做出反应。 通过厚度V1，神经元在称为超列的列中排列 ，每列都大致响应视野的一小部分。 但是，并非超级列中的所有神经元都是相同的：除了识别明暗区域外，每个神经元还专门识别局部面部-将图像的一部分中的明暗区域分开的线-一定的方向。 有些识别出水平的面，有些识别出垂直的面，另一些识别成45度角的面，依此类推。 每个超列都包含具有所有首选方向的神经元列；因此，一个超列可以响应视野中特定区域中所有方向的面部。 超列的组成和方向偏好使我们能够识别视觉世界的轮廓，表面和纹理。


V1中的连接：超列中的神经元与大多数其他神经元相互作用。 但是，仅当列沿其方向放置时，它们才会与其他超列中的神经元发生反应，并且神经元具有相同的方向偏好。

近年来，已经收集了很多解剖学证据，说明神经元如何以不同的方向偏好相互交互。 在它们的地理列中，神经元会与其他大多数神经元发生交互作用，而不管它们的偏好如何。 但是，至于其他超列的神经元，它们的选择性更高，仅与具有相似偏好的神经元相互作用，从而确保我们能够识别视觉世界中的连续轮廓。

Breslov与Cowan，数学家Martin Golubitsky和其他科学家一起，对Cowen和Ermentraut的原始模型进行了概括，以考虑到这些新的解剖学证据。 他们再次将平面用作V1模型的基础：每个超柱在平面上由一个点（x，y）表示，每个点（x，y）对应一个超柱。 具有特定方向θ（其中θ是0和π之间的角度）的神经元由超柱（x，y）的位置与角度θ一起表示-也就是说，它们由信息的三个单位（x，y，θ）表示。 V1模型不是平面，而是每个点具有完整方向的平面。


如果两个元素（x，y，θ）和（s，t，θ）相互作用，则其他具有相同方向的元素在点（x + a，y + b）和（s + a，t + b ），以及在（x，-y）和（s，-t）点具有-θ方向的元素。

为了符合解剖学证据，Breslov及其同事建议，点（x ₀ ，y ₀ ， _θ0 ）指示的神经元与同一超列（x ₀ ，y ₀ ）中的所有其他神经元相互作用。 但是，只有当其他超列的神经元处于首选方向_θ0时 ，它才能与其他神经元相互作用：在平面上，您需要以点_θ0穿过点（x ₀ ，y ₀ ）画一条线。 然后，由点（x ₀ ，y ₀ ， _θ0 ）表示的神经元仅与位于同一条线上，即具有相同的首选方向θ0​​的超柱的神经元相互作用。

此交互方案非常对称。 例如，当平面在任何方向上移动任何距离时，它都不会改变：如果两个元素（x ₀ ，y ₀ ， _θ0 ）和（s ₀ ，t ₀ ，φ0）相互作用，则通过该位移获得的元素，某些a和b的（x ₀ + a，y ₀ + b， _θ0 ）和（s ₀ + a，t ₀ + b，φ0）以相同的方式相互作用。 根据相同的原理，该方案对于平面的旋转和反射是不变的。


由数学模型创建的晶格幻觉。 它非常类似于吸食大麻时产生的幻觉。

Breslov和同事使用原始模型中方程的通用版本来开发系统。 结果是，该模型不仅在V1的解剖结构方面更准确，而且还能够在原始模型无法提供的视场中生成几何图案。 其中包括格子隧道，蜂窝和蜘蛛网，其轮廓的方向比明亮和黑暗的对比区域更好地表征了它们。

此外，该模型对神经元相互作用方案的对称性很敏感：数学家已经证明正是这些对称性导致了神经活动周期性模式的形成。 因此，该模型假设幻觉会引起超柱的排列和方向偏好，即有助于我们识别视觉世界的面孔，轮廓，表面和纹理的机制。 当这些机制失去稳定性时，例如，由于暴露于药物，就会出现活动模式，变成视觉幻觉。

幻觉之外

布雷斯洛夫模型不仅可以让人们深入了解产生视觉幻觉的机制，而且还可以从更广泛的意义上提供有关大脑结构的线索。 布雷斯洛夫和他的妻子，一名实验神经生物学家，一起研究了正常视觉下的超柱连接轮廓，以了解视觉图像的处理方式。 人们习惯于相信V1中的神经元仅定义局部面孔，而人们需要深入大脑以收集这些面孔并识别更复杂的事物，例如轮廓和表面。 但是从与妻子的工作中可以明显看出，V1中的这些结构实际上允许视觉皮层在早期识别轮廓并进行更全面的处理。 人们认为，我们处理的图像越来越复杂，在大脑的层次结构中越来越高。 现在变得很清楚，在皮质的上部和下部之间存在主动反馈。“这不是一个简单的分层过程，而是一个令人难以置信的复杂而活跃的系统，需要花费很多年才能理解。”

这项工作的实际应用包括计算机视觉-计算机科学家已经在构建具有内部连接的结构，布雷斯洛夫和他的同事们玩这些结构来建立模型，以教计算机如何定义轮廓和纹理。如果您表现出一点想象力，您可以想象这项研究有一天将能够帮助恢复残疾人的视力。布雷斯洛夫说：“问题是，是否有可能以某种方式刺激视觉皮层的一部分，绕过眼睛，并使用它来定向盲人。” “如果您了解皮质的结构以及其对刺激的反应，那么也许将有可能发明出正确刺激皮质的最佳方法。”

甚至有一些与大脑完全无关的应用领域。布雷斯洛夫将通过他的工作获得的思想应用于物体处于特定方向的空间中的其他情况，例如来自人和动物组织的成纤维细胞。他表明，在某些条件下，这些相互作用的细胞和分子可以排列并产生类似于V1中出现的模式。

人们谈论从一开始就看到幻觉，在几乎所有文化中，幻觉的图像甚至都可以在岩画中找到。和洞穴壁画。在世界各地的萨满教徒的传统中，它们被视为来自精神世界的信息。很少有现代神经科学家会同意精神的参与，但是作为隐性世界的使者-这次是我们大脑的隐性世界-，这些幻觉并没有失去其潜力。