
普通人中的“模糊”是数字图像处理中的模糊效果。 它本身可以非常有效,可以作为界面动画的一部分,也可以作为更复杂的派生效果(bloom / focusBlur / motionBlur)使用。 有了这些,额头上的诚实忧郁就相当缓慢。 通常,目标平台中内置的实现还有很多需要改进的地方。 要么速度令人伤心,要么人造物伤害了眼睛。 这种情况产生了许多折衷的实现方式,它们或多或少适合某些条件。 原始的实现方案具有良好的可靠性和最高的速度,而对硬件的依赖性最低,正在等待您的选择。 祝您好胃口!
(拉普拉斯模糊-建议的原始算法名称)
今天,我的内部恶魔踢了我,迫使我写了一篇必须在六个月前写的文章。 作为业余爱好者,为了休闲地开发原始效果算法,我想向公众提供一种“几乎是高斯的模糊”算法,其特征是使用了非常快的处理器指令(移位和遮罩),因此可以被微控制器实现(在有限的环境中非常快)。
根据我在Habr上撰写文章的传统,我将以JS作为最受欢迎的语言来举例说明,无论您信不信,这对于快速建立算法原型非常方便。 此外,类型数组还具有在JS上有效实现此功能的能力。 在我不是很强大的笔记本电脑上,全屏图像以30fps的速度处理(不涉及工作线程的多线程处理)。
酷数学免责声明我会马上说我要脱下帽子,因为我认为自己在基础数学上不够熟练。 但是,我始终以基本方法的一般精神为指导。 因此,在欺骗我的“观察性”近似方法之前,请注意计算算法的位复杂度,正如您认为的那样,可以通过经典的多项式逼近方法获得该算法。 我猜对了吗? 您想快速估算它们吗? 鉴于它们需要浮点运算,因此它们将比单个位移慢得多,我将在最后解释。 总之,不要急于理论原教旨主义,也不要忘记我解决问题的背景。
此处存在此描述的目的是为了解释导致我进入结果的我的思想和猜想的过程。 对于那些感兴趣的人:
原始高斯函数:
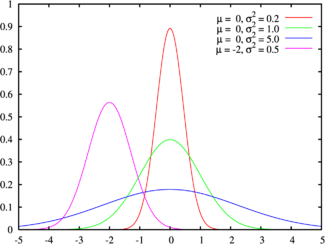
g(x)= a * e **(-((xb)** 2)/ c),其中
a是振幅(如果每个通道有八位颜色,则= 256)
e是欧拉常数〜2.7
b-x中的图形移位(我们不需要= 0)
c-影响与其关联的图的宽度的参数,约为〜w / 2.35
我们的私有函数(从指数中减去负值,再除以乘除数):
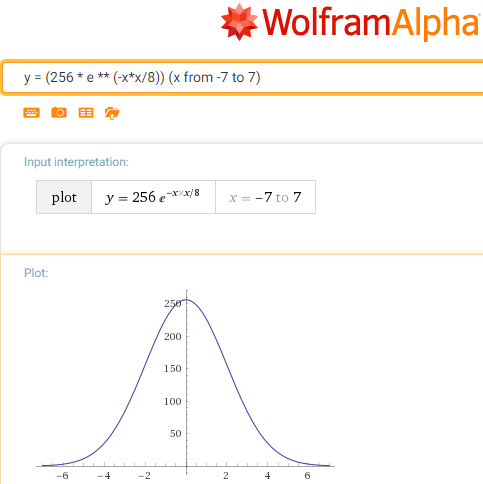
g(x)= 256 / e **(x * x / c)
让脏近似动作开始:
请注意,参数c非常接近半角并设置为8(这是由于每个8位通道可以移位多少步)。
但是,我们也将e粗略地替换为2,并指出这对“铃”的曲率的影响大于其边界。 实际上,它影响2 / e倍,但是令人惊讶的是,该误差补偿了参数c,因此边界条件仍然是有序的,并且该误差仅出现在图形的稍微不正确的“正态分布”中算法,这将影响渐变颜色过渡的动力学,但是用眼睛几乎看不到。
所以现在我们的功能如下:
gg(x)= 256/2 **(x * x / 8)或gg(x)= 2 **(8-x * x / 8)
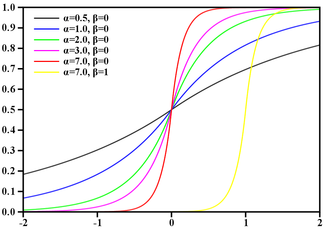
请注意,指数(x * x / 8)的值范围[0-8]与低阶Abs(x)的函数相同,因此,后者适合替换。 我们通过查看图表的变化来快速检查猜测:gg(x)= 256 /(2 ** abs(x)):
高斯模糊与拉普拉斯模糊:
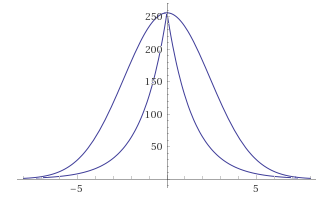
偏差似乎太大,此外,失去平滑性的功能现在达到顶峰。 可是
首先,不要忘记通过模糊获得的梯度的平滑度不取决于概率密度函数(即高斯函数),而是取决于其积分-分布函数。 那时,我还不知道这个事实,但是实际上,在对概率密度函数(Gauss)进行了“破坏性”逼近之后,分布函数仍然非常相似。
那是:
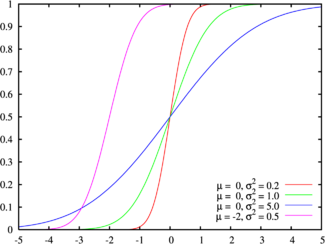
它变成了:
取自现成算法的证明符合:
(展望未来,我会说我的算法相对于高斯x5的模糊误差仅为3%)。
因此,我们离拉普拉斯分布函数越来越近。 谁会想到的,但是他们可以洗97%的图像,而且还不错。
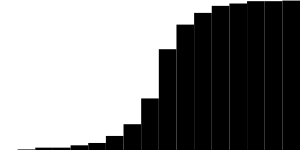
证明,差异高斯模糊x5和“拉普拉斯模糊” x7:

(这不是黑色图像!您可以在编辑器中学习)
这种转换的假设使我们可以继续通过迭代过滤来获取值的想法,我最初计划将其减少。
在讲一种特定的算法之前,如果我先行一步并立即描述它的唯一缺点,那将是很诚实的(尽管实现可能会因速度降低而固定下来)。 但是,该算法是使用剪切算法实现的,并且2的幂是其局限性。 因此,将原始图像制作为使x7模糊(在测试中,x7与高斯x5最接近)。 这种实现限制是由于以下事实:使用八位颜色(每步将滤波器驱动器中的值移位一位),从该点开始的任何动作最多以8步结束。 我还通过比例和附加添加实现了一个稍慢的版本,该版本实现了1.5的快速除法(结果是x15的半径)。 但是随着这种方法的进一步应用,误差增加了,速度下降了,这不允许像这样使用它。 另一方面,值得注意的是,x15已经足够以至于不注意差异,其结果是从原始图像或降采样后的图像中获得的。 因此,如果您在有限的环境中需要非凡的速度,则该方法非常适合。
因此,该算法的核心很简单,执行了四个相同类型的遍:
1.将驱动器t的一半值(最初等于零)加到下一个像素的一半值上,并将结果分配给它。 继续这种方式直到图像行的结尾。 对于所有行。
完成第一遍后,图像会在一个方向上模糊。
2.到第二遍,我们对所有行都沿相反的方向执行相同的操作。
我们得到的图像在水平方向上完全模糊。
3-4。 现在,垂直执行相同的操作。
做完了!
最初,我使用了两次遍历算法来实现整个堆栈的反向模糊处理,但是这很难理解,不能令人满意,并且在当前体系结构上速度较慢。 也许单程算法在微控制器上会更快,加上逐步输出结果的能力也将是一个加分。
在当前的四向实现方法中,我从以前的专家那里研究了模糊算法上的Habré。
habr.com/post/151157我借此机会向他表示声援和深切谢意。
但是黑客并没有就此结束。 现在介绍如何在一个处理器指令中计算所有三个颜色通道! 事实是,被除以2的位移使您可以很好地控制结果位的位置。 唯一的问题是通道的较低位会滑入相邻的较高位,但是您可以重置它们,而不是解决问题,而只是准确性有所降低。 并且根据所描述的过滤器公式,将驱动器的值的一半与下一个单元的值的一半相加(取决于重置放电位)决不会导致溢出,因此您不必担心。 同时计算所有数字的过滤器公式变为:
buf32 [i] = t =(((t >> 1)&0x7F7F7F)+(((buf32 [i] >> 1)&0x7F7F7F));
但是,还需要增加一点:通过实验发现,该公式的准确性损失太大,图像的亮度在视觉上明显跳变。 显然,丢失的位需要四舍五入到最接近的整数,而不是丢弃。 在整数算法中执行此操作的一种简单方法是在除法之前将除数增加一半。 我们的除数是2,因此您需要在所有数字中加一个-常数0x010101。 但是,除此以外,还必须提防溢出。 因此,我们不能使用这种校正来计算下一个单元格的一半值。 (如果有白色,我们将溢出,因此我们将不对其进行校正)。 但是事实证明,主要错误是由驱动器的多次划分造成的,我们可以纠正此错误。 因为,实际上,即使进行了这样的校正,驱动器中的值也不会超过254。但是,当将其添加到0x010101时,将无法保证溢出。 经过校正的过滤器公式采用以下形式:
buf32 [i] = t =((((((0x010101 + t)>> 1)&0x7F7F7F)+(((buf32 [i] >> 1)&0x7F7F7F));
实际上,该公式的校正效果非常好,因此当您对该图像重复应用该算法时,伪影仅在后十遍才开始可见。 (不是重复高斯模糊不会产生此类伪像的事实)。
此外,还有一个很棒的酒店,拥有许多通行证。 (这不是由于我的算法,而是由于正态分布的“正态性”)。 在Laplace Blura的第二遍中,概率密度函数(如果我认为正确的话)将如下所示:
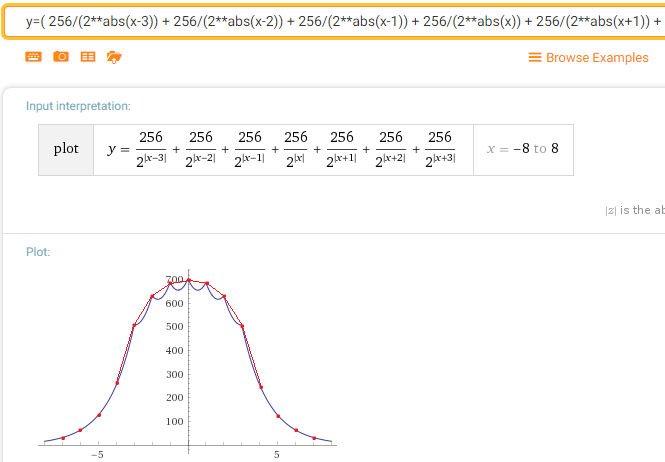
您会发现,它已经非常接近高斯。
根据经验,我发现成对使用大半径修改是允许的,因为 如果最后一次通过的精度更高,则上述属性可以补偿错误(最准确的方法是此处所述的x7模糊算法)。
演示说唱鳕鱼对酷数学家的吸引力:
知道单独使用这种滤波器的正确性会很有趣,我不确定是否有对称分布图。 虽然看不到眼睛的异质性。
upd:在这里,我将提出一些有用的链接,这些链接由评论员友好地提出,并可以从其他Khabrovites中找到。
1.基于SSE的功能,英特尔向导如何工作
-software.intel.com/zh-cn/articles/iir-gaussian-blur-filter-implementation-using-intel-advanced-vector-extensions (感谢
vladimirovich )
2.基于主题“快速图像卷积”的理论及其与诚实高斯
蓝调有关的一些自定义应用程序
-blog.ivank.net/fastest-gaussian-blur.html (感谢
Grox )
欢迎提出建议,意见,建设性批评!