哈Ha
在
Geektimes Habr上已经有几篇有关abc假设的
文章 (例如,
在2013年和
2018年 )。 关于一个定理的故事本身,首先不能被证明多年,然后不能被证明相同的年限,当然至少应该有一部故事片。 但是,在这个奇妙的故事的阴影下,定理本身也被肤浅地认为是太肤浅了,尽管它同样有趣。 至少已经有了一个事实,即abc假设是现代科学中少数未解决的问题之一,即使五年级学生也能理解该问题。 如果这个假设是真的,那么它很容易从其他重要定理的证明
中得出 ,例如,
费马定理的证明。
在不要求Motizuki桂冠的情况下,我
也决定尝试并决定用计算机检查假设中所承诺的平等是否得到满足。 实际上,为什么不-现代处理器不仅要玩游戏-为什么不将计算机用于主要(计算)目的...
谁在乎,发生了什么事,在猫的下面。
问题陈述
让我们从头开始。 该定理是关于什么的? 正如
Wikipedia所说(英语版本中的措词稍微清晰些),对于互质数(没有共同的因数),数字a,b和c使得a + b = c,对于任何ε> 0
,三元组a + b的
数量有限 = c,这样:
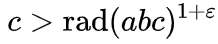
rad函数称为
自由基(radical) ,它表示多个素数的乘积。 例如,rad(16)= rad(2 * 2 * 2 * 2)= 2,rad(17)= 17(17是质数),rad(18)= rad(2 * 3 * 3)= 2 * 3 = 6,弧度(1,000,000)=弧度(2 ^ 6⋅5 ^ 6)= 2 * 5 = 10。
实际上,该定理的实质是此类三元组的数量非常小。 例如,如果我们随机取ε= 0.2并等于100 + 27 = 127:rad(100)= rad(2 * 2 * 5 * 5)= 10,rad(27)= rad(3 * 3 * 3)= 3, rad(127)= 127,rad(a * b * c)= rad(a)* rad(b)* rad(c)= 3810,3810 ^ 1.2明显大于127,不等式不成立。 但是也有例外,例如,对于等式49 + 576 = 625,满足定理的条件(希望的人可以自行检查)。
根据定理,对我们而言,下一个关键时刻是这些等式的数量有限。 即 这意味着您可以简单地尝试在计算机上将它们全部分类。 结果,这给了我们
诺贝尔奖相当有趣的编程任务。
因此,让我们开始吧。
源代码
第一个版本是用Python编写的,尽管这种语言对于这种计算而言太慢了,但是在其上编写代码既简单又容易,这对原型设计很方便。
求根 :我们将数字分解为素数,然后删除重复项,将数组转换为集合。 然后,只需获取所有元素的乘积即可。
def prime_factors(n): factors = []
互质数 :
分解数字,然后检查集合的交集。
def not_mutual_primes(a,b,c): fa, fb, fc = prime_factors(a), prime_factors(b), prime_factors(c) return len(fa.intersection(fb)) == 0 and len(fa.intersection(fc)) == 0 and len(fb.intersection(fc)) == 0
检查 :我们使用已经创建的函数,这里的一切都很简单。
def check(a,b,c): S = 1.2
那些愿意的人可以通过将以上代码复制到任何在线Python语言编辑器中来独立进行实验。 当然,代码可以按预期运行,将所有三元组枚举到至少一百万将太长。 扰流板下方有一个优化版本,建议使用它。
最终版本使用多线程和一些优化在C ++中进行了重写(在C中使用相交集工作可能会变得很困难,尽管可能更快)。 源代码位于扰流器下,可以在免费的g ++编译器中进行编译,代码可以在Windows,OSX甚至Raspberry Pi上运行。
对于那些懒于安装C ++编译器的人,提供了稍微优化的Python版本,该版本可以在任何在线编辑器中运行(我使用
https://repl.it/languages/python )。
Python版本 from __future__ import print_function import math import time import multiprocessing prime_factors_list = [] rad_list = [] def prime_factors(n): factors = []
结果
三,三,三,三的确很少。
一些结果如下:
N = 10 :1“三”,交货时间<0.001c
1 + 8 = 9
N = 100 :2个“三重”,运行时间<0.001c
1 + 8 = 9
1 + 80 = 81
N = 1000 :8个“三元组”,运行时间<0.01c
1 + 8 = 9
1 + 80 = 81
1 + 242 = 243
1 + 288 = 289
1 + 512 = 513
3 + 125 = 128
13 + 243 = 256
49 + 576 = 625
N = 10000 :23个“三元组”,运行时间2秒
Threes A,B,C最多100001 + 8 = 9
1 + 80 = 81
1 + 242 = 243
1 + 288 = 289
1 + 512 = 513
1 + 2400 = 2401
1 + 4374 = 4375
1 + 5831 = 5832
1 + 6560 = 6561
1 + 6655 = 6656
1 + 6859 = 6860
3 + 125 = 128
5 + 1024 = 1029
10 + 2187 = 2197
11 + 3125 = 3136
13 + 243 = 256
49 + 576 = 625
1331 + 9604 = 10935
81 + 1250 = 1331
125 + 2187 = 2312
243 + 1805 = 2048
289 + 6272 = 6561
625 + 2048 = 2673
N = 100000 :53个三连冠,运行时间50c
Threes A,B,C高达100,0001 + 8 = 9
1 + 80 = 81
1 + 242 = 243
1 + 288 = 289
1 + 512 = 513
1 + 2400 = 2401
1 + 4374 = 4375
1 + 5831 = 5832
1 + 6560 = 6561
1 + 6655 = 6656
1 + 6859 = 6860
1 + 12167 = 12168
1 + 14336 = 14337
1 + 57121 = 57122
1 + 59048 = 59049
1 + 71874 = 71875
3 + 125 = 128
3 + 65533 = 65536
5 + 1024 = 1029
7 + 32761 = 32768
9 + 15616 = 15625
9 + 64000 = 64009
10 + 2187 = 2197
11 + 3125 = 3136
13 + 243 = 256
28 + 50625 = 50653
31 + 19652 = 19683
37 + 32768 = 32805
49 + 576 = 625
49 + 16335 = 16384
73 + 15552 = 15625
81 + 1250 = 1331
121 + 12167 = 12288
125 + 2187 = 2312
125 + 50176 = 50301
128 + 59049 = 59177
169 + 58880 = 59049
243 + 1805 = 2048
243 + 21632 = 21875
289 + 6272 = 6561
343 + 59049 = 59392
423 + 16384 = 16807
507 + 32768 = 33275
625 + 2048 = 2673
1331 + 9604 = 10935
1625 + 16807 = 18432
28561 + 89088 = 117649
28561 + 98415 = 126976
3584 + 14641 = 18225
6561 + 22000 = 28561
7168 + 78125 = 85293
8192 + 75843 = 84035
36864 + 41261 = 78125
在
N = 1,000,000的情况下,我们只有102个“三元组”,在扰流器下给出了完整的列表。
Threes A,B,C高达1,000,0001 + 8 = 9
1 + 80 = 81
1 + 242 = 243
1 + 288 = 289
1 + 512 = 513
1 + 2400 = 2401
1 + 4374 = 4375
1 + 5831 = 5832
1 + 6560 = 6561
1 + 6655 = 6656
1 + 6859 = 6860
1 + 12167 = 12168
1 + 14336 = 14337
1 + 57121 = 57122
1 + 59048 = 59049
1 + 71874 = 71875
1 + 137780 = 137781
1 + 156249 = 156250
1 + 229375 = 229376
1 + 263168 = 263169
1 + 499999 = 500000
1 + 512000 = 512001
1 + 688127 = 688128
3 + 125 = 128
3 + 65533 = 65536
5 + 1024 = 1029
5 + 177147 = 177152
7 + 32761 = 32768
9 + 15616 = 15625
9 + 64000 = 64009
10 + 2187 = 2197
11 + 3125 = 3136
13 + 243 = 256
13 + 421875 = 421888
17 + 140608 = 140625
25 + 294912 = 294937
28 + 50625 = 50653
31 + 19652 = 19683
37 + 32768 = 32805
43 + 492032 = 492075
47 + 250000 = 250047
49 + 576 = 625
49 + 16335 = 16384
49 + 531392 = 531441
64 + 190269 = 190333
73 + 15552 = 15625
81 + 1250 = 1331
81 + 123823 = 123904
81 + 134375 = 134456
95 + 279841 = 279936
121 + 12167 = 12288
121 + 255879 = 256000
125 + 2187 = 2312
125 + 50176 = 50301
128 + 59049 = 59177
128 + 109375 = 109503
128 + 483025 = 483153
169 + 58880 = 59049
243 + 1805 = 2048
243 + 21632 = 21875
289 + 6272 = 6561
338 + 390625 = 390963
343 + 59049 = 59392
423 + 16384 = 16807
507 + 32768 = 33275
625 + 2048 = 2673
864 + 923521 = 924385
1025 + 262144 = 263169
1331 + 9604 = 10935
1375 + 279841 = 281216
1625 + 16807 = 18432
2197 + 583443 = 585640
2197 + 700928 = 703125
3481 + 262144 = 265625
3584 + 14641 = 18225
5103 + 130321 = 135424
6125 + 334611 = 340736
6561 + 22000 = 28561
7153 + 524288 = 531441
7168 + 78125 = 85293
8192 + 75843 = 84035
8192 + 634933 = 643125
9583 + 524288 = 533871
10816 + 520625 = 531441
12005 + 161051 = 173056
12672 + 117649 = 130321
15625 + 701784 = 717409
18225 + 112847 = 131072
19683 + 228125 = 247808
24389 + 393216 = 417605
28561 + 89088 = 117649
28561 + 98415 = 126976
28561 + 702464 = 731025
32768 + 859375 = 892143
296875 + 371293 = 668168
36864 + 41261 = 78125
38307 + 371293 = 409600
303264 + 390625 = 693889
62192 + 823543 = 885735
71875 + 190269 = 262144
131072 + 221875 = 352947
132651 + 588245 = 720896
the,程序仍然运行缓慢,我没有等待结果N = 10000000,计算时间超过了一个小时(也许我在某个地方对算法进行了优化时犯了一个错误,我可以做得更好)。
以图形方式查看结果更加有趣:
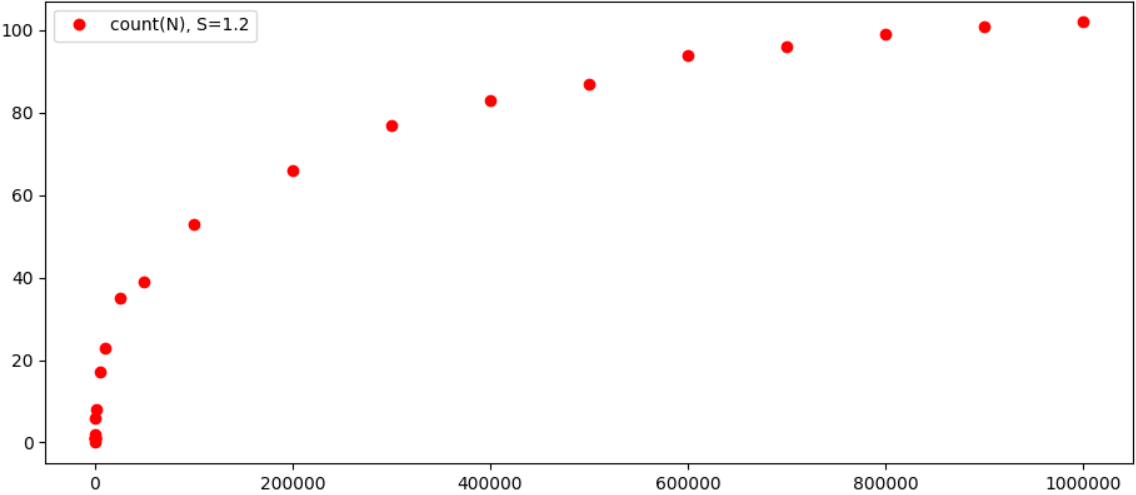
原则上,很明显,可能的三元组数目对N的依赖性明显比N本身慢,并且对于每个ε,结果可能收敛到某个特定的数目。 顺便说一下,随着ε的增加,三元组的数量显着减少,例如,对于ε= 0.4,对于N <100000,我们只有2个等式(1 + 4374 = 4375和343 + 59049 = 59392)。 因此,一般而言,该定理似乎确实成立(嗯,可能已经在功能更强大的计算机上进行了测试,也许所有这些都已经很久了)。
那些愿意的人可以自己尝试,如果有人的结果达到10,000,000或更高,我很乐意将其添加到文章中。 当然,对“三元组”完全停止增长之前的“计数”会很有趣,但是这可能会花费很长时间,计算速度似乎取决于N为N * N(或N ^ 3),并且过程很长 但是,附近有一件了不起的事情,希望的人可能会加入搜索。
编辑:如评论中所建议,维基百科已经有了一个
包含结果的
表 -在N到10 ^ 18范围内,“三联”的数量仍在增长,因此尚未找到该集合的“终点”。 更有趣的是-阴谋仍然保留。