2016年3月，斯坦福大学的Robert J. Lemke-Oliver和Kannan Sundararajan
开创了素数分布的
新格局 。 事实证明，质数
专门分布在数字空间上。 有关更多详细信息，请参见Habré上文章
“素数的结构和随机性”的翻译。
来自其他领域（包括化学领域）的专家参加了该主题的研究。 并成功。 理论化学教授
Salvatore Torcuato与数字理论家
Matthew de Courcy-Ireland一起发现了以前未知的素数分布
新模式 。 事实证明，质数的分布形成了分形状的衍射图样，与异质准晶体的衍射图样有些相似。
Torcuato教授专门研究物理系统结构（例如晶体和胶体）中的图案。 研究结构的标准方法是X射线衍射。 液体或气体中的随机分子会在所有方向上反射光线，而不会产生明显的图案。 但是晶体中对称放置的原子会同步反射光波，从而产生周期性的明显衍射（
布拉格峰 ）的亮点。 通过对布拉格峰的分析，可以了解产生此类图像的晶体或其他材料的内部结构。
因此，在Torkuato等人的新科学文章（
1、2、3 ）中，证明了在素数分布中发现的有序结构只不过是类似于准晶体的分形衍射图样。
素数晶格上的布拉格峰图像类似于准晶体，但仍与它们不同。 Torcuato
说 ，素数作为物理系统“是一种全新的结构类别”。 研究人员将这种新的类似分形的模式称为“有效极限周期”。
该图由反映最常见的质数间隔的明亮峰的周期性序列组成：它们都是奇数（除2外），许多彼此相邻。 最亮的峰（由两位分开的对）以规则的间隔交替出现，而亮峰较少，反映了由六位分开的质数。 在它们之间甚至还有更暗的峰，对应于更远的素数对，等等。所有这些都是无限数量的彼此放置的布拉格峰。
较早地在准晶体的衍射图中观察到了类似的布拉格峰结构。
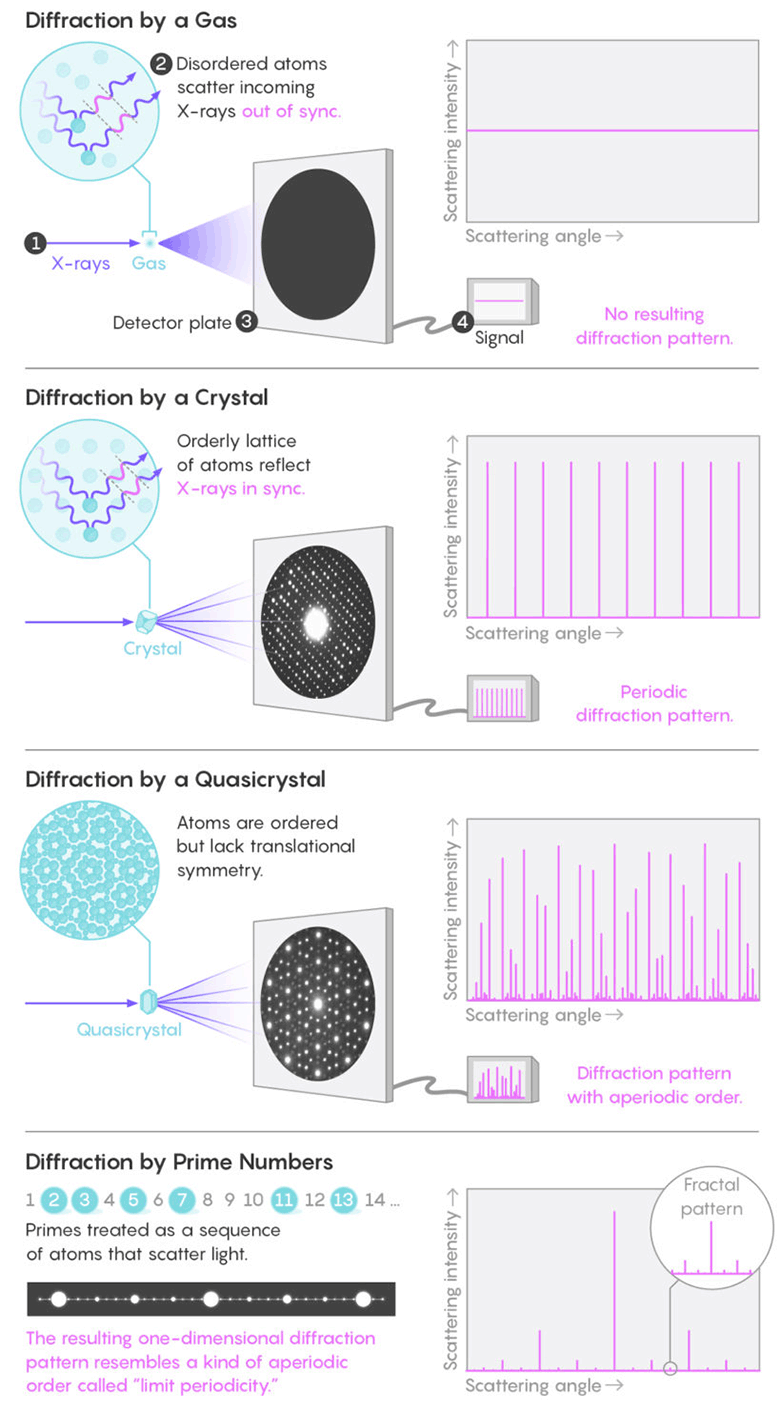液体或气体中的随机分子会在所有方向上反射光线，而不会产生明显的图案。 但是晶体中对称放置的原子会同步反射光波，从而产生周期性的明显衍射的亮点。 事实证明，质子的分布图案形成了与准晶体相似的分形衍射图案。准晶体是1980年代发现的奇怪材料。 它们的特点是经典晶体学中禁止对称，并且存在远距离有序。 著名的
彭罗斯（Penrose）马赛克类型的非周期性马赛克是准晶体的数学模型。 在这些镶嵌物中，不存在平移对称性，存在重复性和准结晶度（五阶对称性）。
彭罗斯（Penrose）马赛克类型P1的片段（来自六种类型的瓷砖）在素数的情况下，峰之间的距离彼此成正比，这与准晶体的布拉格峰不合理地间隔相反。 Torcuato
说： “素数实际上意味着粒子位置的状态完全不同，类似于准晶体，但不像准晶体。”
衍射图样的发现不能称为数论的突破性发现，因为这些图谱的主要部分先前已经通过其他数学方法（而不是通过准晶体的衍射）进行了描述。 因此，使用衍射图样，可以预测类型17和19的“双精度”-这与
第一个Hardy – Littlewood假设的数学等价性有关，该
假设关于数字线的给定段上素数元组的存在。 其中一条规则禁止在{3，5，7}之后使用三连串的连续奇数。 这也解释了为什么衍射图中下一个最亮的布拉格峰对应于由六位而不是四位分隔的数字。
一项新的科学著作只是对素数的均匀分布问题的重新审视，并且是一种为素数推导特定“单一定律”的简便方法。 此外，这是从晶体学的角度分析数学问题的一种不寻常的方法，即从一个相对较年轻的研究领域（称为“非周期性”）的角度来看，该非周期性的模型处于晶体学，动力学系统，谐波分析和离散几何学的交集处。 发现准晶体后，很明显，以前的方法在这里行不通，科学的这一分支便发展起来了。
自1950年代以来，素数的分布类似于一种特殊的非周期性分布。 这称为极限周期性。 在这样的系统中，周期性间隔嵌套在无限的层次结构中，因此在任何间隔中，系统都包含仅在较大间隔中重复的模式部分，如泰勒-索科拉尔贴图所示。
泰勒-萨科拉瓷砖理论计算表明，物质的最大周期性相应能够在自然界形成，并且此类系统可能具有不同寻常的特性。 但是没有人猜测将极限周期与素数联系起来。 现在我们知道存在这样的联系，并且素数显示出一种新的极限周期性-“有效”极限周期性，因为整个统计系统中素数之间距离的同步性是观察到的。
问题出现了：素数分布中的模式如何影响密码算法的强度？
“关于这个主题，我收到了很多封信。 著名密码学家布鲁斯·施耐尔
（ Bruce Schneier
）在他的博客中
写道 ，尽管这是一项有趣的研究，但它与密码学无关。 -密码学家对寻找素数甚至分布不感兴趣。 RSA类型的公共密钥密码算法的强度与因质数乘积而分解大复合数的困难有关。 这是完全不同的事情。”
因此，尽管在素数分布的研究方面取得了进展，但仍无需担心密码的强度。
