大家好! 本文将重点讨论数字信号处理的一个重要部分-窗口信号过滤,尤其是在FPGA上。 本文将展示如何设计标准长度的经典窗口以及从64K到16M +样本的“长”窗口。 主要开发语言是VHDL,元素库是最新系列的最新Xilinx FPGA晶体:它们是Ultrascale,Ultrascale +,7系列。 本文将演示CORDIC的实现-用于配置任何持续时间的窗口功能的基本内核以及基本窗口功能。 本文介绍了在Vivado HLS中使用高级语言C / C ++的设计方法。 像往常一样,在文章末尾,您将找到一个指向项目源代码的链接。
KDPV:通过DSP节点进行频谱分析任务的典型信号传输方案。
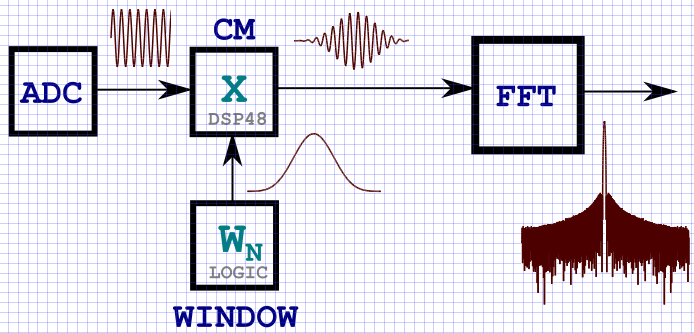
引言
从“数字信号处理”过程中,许多人知道,对于时间无限长的正弦波形,其频谱是信号频率下的增量函数。 实际上,实时限时谐波信号的频谱等效于函数
〜sin(x)/ x ,主瓣的宽度取决于信号分析间隔
T的持续时间
。 时间限制无非就是将信号乘以矩形包络。 从DSP过程中可以知道,时域中的信号乘法是其频谱在频域中的卷积(反之亦然),因此,谐波信号的有限矩形包络的频谱等于〜sinc(x)。 这也是由于以下事实:我们无法在无限的时间间隔内对信号进行积分,并且离散形式的傅立叶变换(通过有限的和表示)受到采样数的限制。 通常,现代FPGA数字处理设备中的FFT长度取
NFFT值从8到几百万个点。 换句话说,在间隔
T上计算输入信号的频谱,该间隔在许多情况下等于
NFFT 。 通过将信号限制为间隔
T ,我们从而强加了一个矩形“窗口”,其持续时间为
T个样本。 因此,所得频谱是谐波信号和矩形包络的频谱。 在DSP任务中,很长时间以来就发明了各种形状的窗口,当它们在时域中叠加到信号上时,可以改善其频谱特性。 大量的各种窗口主要是由于任何窗口覆盖的主要功能之一。 该特征通过旁瓣的水平与中央瓣的宽度之间的关系来表达。 一个众所周知的模式:旁瓣的抑制能力越强,主瓣越宽,反之亦然。
窗口功能的应用之一:通过抑制旁瓣电平,在较强信号的背景下检测弱信号。 DSP任务中的主要窗口函数是三角形,正弦曲线,Lanczos,Hann,Hamming,Blackman,Harris,Blackman-Harris窗口,平顶窗口,Natall,Gauss,Kaiser窗口等。 它们中的大多数通过对具有特定权重的谐波信号求和而通过有限级数表示。 复杂形状的窗口是通过采用指数(高斯窗口)或修改的Bessel函数(Kaiser窗口)来计算的,因此本文中将不考虑。 您可以在文献中阅读有关窗口函数的更多信息,而我通常会在本文结尾给出这些信息。
下图显示了使用Matlab CAD工具构建的典型窗口函数及其光谱特性。

实作
在本文的开头,我插入了KDPV,它以一般术语显示了输入数据与窗口函数相乘的结构图。 显然,在FPGA中实现窗口功能存储的最简单方法是将其写入存储器(块
RAMB或分布式
Distributed-无关紧要),然后在信号的输入采样到达时循环检索数据。 通常,在现代FPGA中,内部存储器的数量允许存储较小尺寸的窗口函数,然后将其与输入的输入信号相乘。 我所说的窗口功能最长可达64K个样本。
但是,如果窗口函数过长怎么办? 例如,1M读数。 很容易计算出,对于以32位位网格显示的这种窗口函数,需要RAMB36K型FPGA Xilinx晶体的NRAMB = 1024 * 1024 * 32/32768 = 1024个块存储单元。 对于1600万个样本? 16000个存储单元! 没有哪个现代FPGA具有如此大的内存。 对于许多FPGA来说,这太多了,而在其他情况下,这是对FPGA资源的浪费(当然,这是客户的钱)。
在这方面,您需要想出一种直接将窗口函数样本直接生成给FPGA的方法,而无需将远程设备的系数写入块存储器。 幸运的是,我们早已发明了基本的东西。 使用诸如
CORDIC (
逐位方法)之类的算法,可以设计许多窗口函数,其公式以谐波信号表示(Blackman-Harris,Hann,Hamming,Nattal等)。
哥迪克
CORDIC是一种简单方便的迭代方法,用于计算坐标系的旋转,它使您可以通过执行基本加法和平移操作来计算复杂的函数。 使用CORDIC算法,可以计算谐波信号sin(x),cos(x)的值,找到相位-atan(x)和atan2(x,y),双曲三角函数,旋转矢量,提取数字的根等。
起初,我想采用成品的CORDIC内核并减少工作量,但是对于Xilinx内核我却很讨厌。 在研究了github上的存储库之后,我意识到呈现的所有内核出于多种原因(适用于特定任务或元素库,文档记录不清晰,不可读,不通用,
以Verilog编写等)不适合使用。 然后我请
拉齐佛同志为我做这项工作。 当然,他应付了它,因为CORDIC的实现是DSP领域中最简单的任务之一。 但是由于我不耐烦,所以在他工作的同时,我
用自己的参数化核心编写了
我的自行车 。 主要功能是
DATA_WIDTH输出信号的可配置位深度以及从-1到1的归一化输入相位
PHASE_WIDTH ,以及
PRECISION计算的精度。 CORDIC内核根据流水线并行电路执行-在每个时钟周期,内核都准备好执行计算和接收输入样本。 内核花费N个周期来计算输出样本,其数量取决于输出样本的容量(容量越大,计算输出值的迭代越多)。 所有计算并行进行。 因此,CORDIC是创建窗口函数的基本核心。
视窗功能
在本文的框架中,我仅实现了通过谐波信号(Hann,Hamming,Blackman-Harris,各种阶数等)表示的那些窗函数。 为此需要什么? 一般而言,构造窗口的公式看起来像一系列有限的长度。

一组特定的系数
a k和该系列的成员确定窗口的名称。 最受欢迎和最常用的是Blackman-Harris窗口:顺序不同(从3到11)。 下表是Blackman-Harris窗口的系数表:

原则上,布莱克曼-哈里斯(Blackman-Harris)窗口集适用于许多光谱分析问题,并且无需尝试使用诸如高斯(Gauss)或凯撒(Kaiser)之类的复杂窗口。 纳塔尔式或平顶式窗户只是一种重量不同的窗户,但其基本原理与布莱克曼·哈里斯(Blackman-Harris)相同。 已知该系列的成员越多,旁瓣电平的抑制作用越强(取决于窗口函数的比特深度的合理选择)。 根据任务,开发人员只需选择使用的窗口类型。
FPGA实现-传统方法
窗口函数的所有内核都是使用经典方法设计的,用于描述FPGA中的数字电路,并以VHDL语言编写。 以下是制作的组件的列表:
- bh_win_7term -Blackman-Harris 7阶,最大程度抑制侧支架的窗口。
- bh_win_5term -Blackman-Harris 5订单,包括带有平顶的窗口。
- bh_win_4term -Blackman-Harris 4个订单,包括Nattal和Blackman-Nattal窗口。
- bh_win_3term -Blackman-Harris 3个订单,
- hamming_win -Hamming和Hann窗口。
Blackman-Harris窗口组件的源代码为3个数量级:
entity bh_win_3term is generic ( TD : time:=0.5ns;
在某些情况下,我使用
UNISIM库将
DSP48E1和DSP48E2节点嵌入到项目中,由于在这些块内进行流水线操作,最终使
我能够提高计算速度,但是正如实践所示,自由束缚和编写
P = A * B + C并在代码中指定以下指令:
attribute USE_DSP of <signal_name>: signal is "YES";
这样可以很好地工作,并严格设置要为合成器实现数学功能的元素的类型。
维瓦多·赫尔斯(Vivado hls)
另外,我使用
Vivado HLS工具实现了所有核心。 我将列出Vivado HLS的主要
优点 :高级语言C或C ++的高速设计(
上市时间 ),由于缺乏时钟频率的概念而对开发的节点进行快速建模,通过介绍解决方案的灵活配置(在资源和性能方面)项目中的实用指示和指令,以及高级语言开发人员的入门门槛低。 与传统方法相比,主要缺点是FPGA资源的成本不理想。 同样,不可能达到经典的旧RTL方法(VHDL,Verilog,SV)所提供的那些速度。 好吧,最大的
缺点是要用铃鼓跳舞,但这是赛灵思所有CAD的特点。 (注意:在Vivado HLS调试器中和实际的C ++模型中,通常会获得不同的结果,因为Vivado HLS利用
任意精度的优势弯曲地工作了)。
下图显示了Vivado HLS中合成的CORDIC内核的日志。 它内容丰富,并显示许多有用的信息:使用的资源数量,内核用户界面,循环及其属性,计算延迟,计算输出值的间隔(在设计串行和并行电路时很重要):

您还可以查看计算各种组件(功能)中数据的方法。 可以看出,在零阶段,读取了阶段数据,并在步骤7和8中显示了CORDIC节点的结果。

Vivado HLS的结果:从C代码创建的综合RTL内核。 日志显示,在时间分析中,内核成功通过了所有限制:

Vivado HLS的另一个重要优点是,为了验证结果,她自己根据用于检查C代码的模型对合成的RTL代码进行了测试。 这可能是一个原始测试,但是我认为比较C和HDL上算法的操作非常凉爽和方便。 以下是Vivado的屏幕截图,显示了Vivado HLS获得的窗口函数的内核函数模型的仿真:

因此,对于所有窗口函数,无论采用哪种设计方法(在VHDL或C ++中),都可获得相似的结果。 但是,在第一种情况下,可以实现更高的工作频率和更少的资源,在第二种情况下,可以实现最大的设计速度。 两种方法都有生命权。
我专门计算了使用不同方法进行开发所花费的时间。 我在Vivado HLS中实现了一个C ++项目,比在VHDL中快了12倍。
方法比较
比较用于CORDIC内核的HDL和C ++的源代码。 如前所述,该算法基于加,减和移位运算。 在VHDL上,它看起来像这样:存在三个数据向量-一个负责角度的旋转,另外两个确定向量沿X和Y轴的长度,这等效于sin和cos(请参见Wiki中的图片):
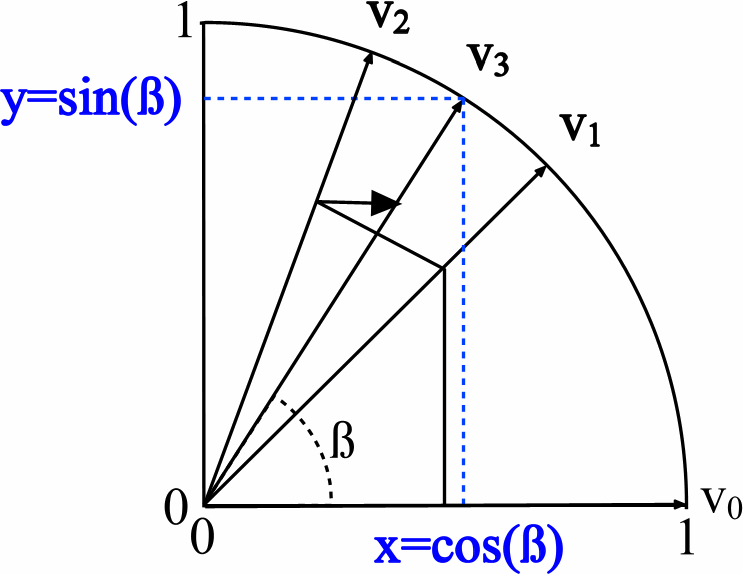
通过迭代计算Z值,可以并行计算X和Y值在HDL上循环搜索输出值的过程:
constant ROM_LUT : rom_array := ( x"400000000000", x"25C80A3B3BE6", x"13F670B6BDC7", x"0A2223A83BBB", x"05161A861CB1", x"028BAFC2B209", x"0145EC3CB850", x"00A2F8AA23A9", x"00517CA68DA2", x"0028BE5D7661", x"00145F300123", x"000A2F982950", x"000517CC19C0", x"00028BE60D83", x"000145F306D6", x"0000A2F9836D", x"0000517CC1B7", x"000028BE60DC", x"0000145F306E", x"00000A2F9837", x"00000517CC1B", x"0000028BE60E", x"00000145F307", x"000000A2F983", x"000000517CC2", x"00000028BE61", x"000000145F30", x"0000000A2F98", x"0000000517CC", x"000000028BE6", x"0000000145F3", x"00000000A2FA", x"00000000517D", x"0000000028BE", x"00000000145F", x"000000000A30", x"000000000518", x"00000000028C", x"000000000146", x"0000000000A3", x"000000000051", x"000000000029", x"000000000014", x"00000000000A", x"000000000005", x"000000000003", x"000000000001", x"000000000000" ); pr_crd: process(clk, reset) begin if (reset = '1') then
在C ++中,在Vivado HLS中,代码看起来几乎相同,但是记录短了几倍:
显然,使用具有移位和加法的相同循环。 但是,默认情况下,Vivado HLS中的所有循环都被“折叠”并按顺序执行,这是针对C ++语言的。
HLS UNROLL或
HLS PIPELINE编译指示的引入将串行计算转换为并行计算。 这导致FPGA资源的增加,但是,它允许您在每个时钟周期计算并向内核提交新值。
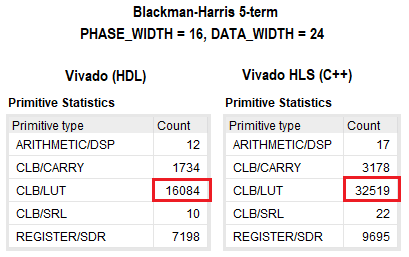
下图显示了该项目在VHDL和C ++中的综合结果。 如您所见,从逻辑上讲,相差两倍于传统方法。 对于其他FPGA资源,差异不明显。 我没有深入研究C ++中的项目,但是通过设置各种指令或部分更改代码可以明确地减少所使用的资源数量。 在这两种情况下,对于给定的〜350 MHz核心频率,时序收敛。
实施功能
由于计算是以定点格式进行的,因此在FPGA上设计DSP系统时,窗口函数具有许多必须考虑的功能。 例如,窗口函数数据的位深度越大,窗口覆盖的准确性越好。 另一方面,在窗口函数的位深度不足的情况下,失真会引入到生成的波形中,这会影响频谱特性的质量。 例如,窗口函数与2 ^ 20 = 1M个采样持续时间的信号相乘时必须至少具有20位。
结论
本文介绍了一种无需使用外部存储器或FPGA块存储器即可设计窗口功能的方法。 给出了仅使用FPGA(在某些情况下为DSP模块)的逻辑资源的方法。 使用CORDIC算法,可以获得任何位深度(在一定范围内),任何长度和顺序的窗口函数,因此实际上具有窗口的任何光谱特征集。
作为其中一项研究的一部分,我设法在频率约为375 MHz的1M样本上获得了5和7个数量级的Blackman-Harris窗函数的稳定工作内核,并且还为频率约为400 MHz的基于CORDIC的FFT生成了旋转系数的生成器。 使用的FPGA Crystal:Kintex Ultrascale +(xcku11p-ffva1156-2-e)。
在此处链接到
github项目 。 该项目包含Matlab中的数学模型,VHDL中窗口函数和CORDIC的源代码,以及C ++中针对Vivado HLS列出的窗口函数的模型。
有用的文章
我还建议一本关于DSP的非常受欢迎的书
-Ayficher E.,Jervis B.数字信号处理。 实用方法感谢您的关注!