TL; DR 一本关于程序员数学的小书。 电子版和纸质版通过引用 。我在大学任教9年。 在这段时间里,学生变了。 我的主观印象是,现代的新生更喜欢他的时间。 在免费参加的条件下,即使是优秀的学生也必须确保特定的讲座对他们有益,这相当于在Kaggle或Coursera上花费1.5个小时。 似乎可以保证质量的解释已经
在破坏经典的演讲形式 。 因此,许多讲师中的第二讲通常是在人数很少的观众面前举行的。 在较小的听众中,学生对问题的应变能力更大,而我成对听到的关于算法和离散化的最常见问题是“为什么?”。
为什么使用组合式公式? 所有这些有条件概率的收获是什么?通常在篮子和球上解释这些条件概率? 为什么要相乘矩阵? 为何需要逆矩阵? 好吧,这是广度优先的搜索,cho?并不是说在我自己的IT学生中,我对所有这些问题都得到了明确的答案。 但是完全不同类型的公司中的经验使我更加了解。 在我的配对中,我尝试给出一些不像猫一样的例子,以建立不明显的类比,并且通常以某种方式使该行业更接近数学。 而且,这些年来我所有班级的总听众不可能超过1000人。 因此,我提出了很多解释,并为程序员编写了带有示例的书。
下面我将给出一个小片段。 您可以通过
单击链接以纸质或电子形式拥有这本书。 欢迎反馈! 追。
莫斯科溜冰场
莫斯科 外面是冬天,不是很冷,阳光充足。 周日早上。 您已经通过线性代数的考试,甚至考试,而且您拥有自己的溜冰鞋。 幸福还需要什么?
你想去溜冰场!
您在一杯茶上制定了一个计划。 您对距房子足够近的溜冰场感兴趣,但这还不够,您仍然需要便利设施。 最好让这些溜冰场免费,配备无线网络和厕所。
您将附近的许多溜冰场称为
A ,将便捷的溜冰场称为
B。 并且由于我们对邻近性和便利性都感兴趣,因此我们的目标是将这些集合A∩B相交
。 我们从哪里得到这些套装?
通过溜冰场或阅读海报评论不是您的方法。 因此,您可以转到
莫斯科开放数据门户网站,或者用Python脚本为您完成此操作,可以在该书的网站上的文档
M02-矢量(滑冰)中找到它的示例。 您会发现莫斯科有很多溜冰场-1350。我们将如何搜索? 在这里,您回想起有关线性代数的教科书,并且了解到需要将滚子映射到所需属性的两个空间:二维坐标
(纬度,经度)和三维便利设施
(Wi-Fi,厕所,免费) 。
在第二个空间中,该属性的存在将为1,并且该缺失将为零,这意味着不再需要对该数据进行规范化。 我们也不会对坐标进行归一化,因为它们在我们的纬度上是可比的(否则,我们将不得不选择一个参考点并将度数转换为米)。 然后,您只选择最有趣的选项-为什么您需要一个溜冰场,它在城市的对面,或者显然没有任何便利设施? 对于任何空间,我们将仅采用距目标欧几里得距离最小的数据。
def topN(expected, data, N): norms = list(map( lambda row, number: (np.linalg.norm(row - expected), number), data, range(len(data))))
一切准备就绪。 只需在我们自己的坐标处窥视(现在可以在任何有地图的应用程序中完成)并找到所有合适的溜冰场
集
A和
B的交集:
me_geo = np.array([37.676289, 55.772266])
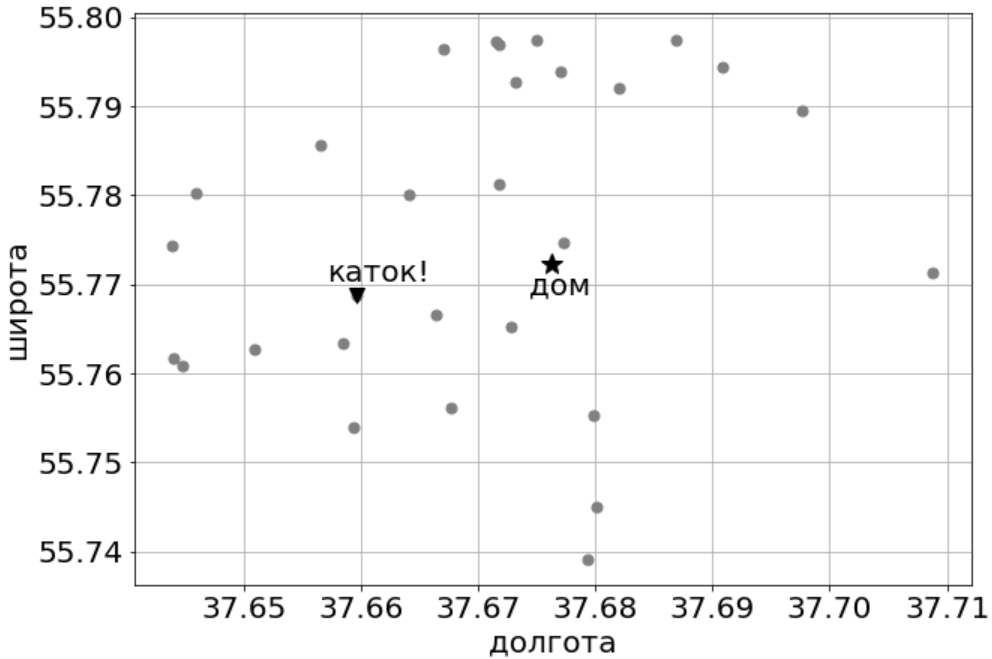
对于该示例中的数据,在最近的30个溜冰场中,我们在Staraya Basmannaya上获得了一个溜冰场,但具有所有便利设施。 而且你甚至可以走路。
尝试使用莫斯科开放数据门户网站来独立查找离您最近的开放式Wi-Fi,夏季电影院或室外视频监控摄像机。