关于多项式时间内的环道问题的可解性

通过学习生物信息学课程，学生可以了解环道问题。特别是，对于程序员而言，最优质和最贴切的精神之一是来自加利福尼亚大学圣地亚哥分校课程中的生物信息学（Pavel Pevzner）课程。 语句的简单性，实际重要性以及通过简单的编码来解决问题的能力仍然被认为是尚未解决的问题，这一问题引起了人们的关注。 问题是通过这种方式提出的。 是否可以在多项式时间内恢复一组点的坐标$$ $内联$ X $内联$ 如果知道它们之间所有成对距离的集合$$ $内联$ \ Delta X $内联$ ？

这个看似简单的任务仍然在计算几何学未解决的问题列表中。 此外，这种情况甚至不涉及多维空间中的点，尤其是弯曲的点，问题已经是最简单的选择-当所有点都具有整数坐标并且位于同一条线上时。

在近半个世纪以来，由于这项任务被数学家认为是一项挑战（Shamos，1975），因此获得了一些结果。 对于一维问题，我们考虑两种情况：

1. 点位于一条直线上（收费问题）
2. 点位于圆上（皮带道问题）

这两个案例使用不同的名称是有原因的-解决它们需要采取不同的努力。 的确，第一个问题已经足够快地解决了（在15年内），并且建立了回溯算法，该算法平均可以在二次时间内恢复解决方案$$ $内联$ O（n ^ 2 \ log n）$内联$ 在哪里$$ $内联$ n $内联$ -点数（Skiena，1990年）； 对于第二项任务，到目前为止尚未完成，并且提出的最佳算法具有指数计算复杂性$$ $ inline $ O（n ^ n \ log n）$内联$ （Lemke，2003）。 下图显示了您的计算机将为多点数量的集合获得解决方案的估计时间。



也就是说，在心理上可接受的时间内（约10秒），您可以恢复许多$$ $内联$ X $内联$ 收费公路箱的最高赔付点为1万分，环线公路箱的最高赔付点为10分，这在实际应用中绝对是毫无价值的。

一点澄清。 据信，收费公路问题是在实际使用中解决的，即针对所遇到的绝大多数数据。 在这种情况下，纯数学家的反对意见是存在一些特殊的数据集，而对于这些数据集，以指数形式获得解的时间将被忽略$$ $内联$ O（2 ^ n \ log n）$内联$ （Zhang，1982）。 与收费公路相比，带指数算法的环城公路问题无法以任何方式解决。

从生物信息学角度解决环城公路问题的重要性

20世纪末，人们发现了一种新的生物分子合成途径，称为非核糖体合成途径。 它与经典合成途径的主要区别是最终合成结果根本不编码到DNA中。 取而代之的是，只有可以收集这些对象的“工具”（许多不同的合成器）的代码才被写入DNA。 因此，生物机器工程得到了极大的丰富，而不是仅使用20种标准零件（标准氨基酸，也称为蛋白原性）的单一类型的收集器（核糖体），出现了许多其他类型的收集器，它们可以使用500多个标准和非标准零件（非蛋白原氨基酸及其各种修饰）。 这些组装者不仅可以将零件连接成链，而且可以获得非常复杂的结构-循环，分支以及具有许多循环和分支的结构。 所有这些显着增加了细胞在其各种寿命情况下的武库。 这样的结构的生物活性高，特异性（作用的选择性）也高，各种性质不受限制。 在英语文献中，这些细胞产物的类别称为NRP（非核糖体产物或非核糖体肽）。 生物学家希望，正是在这种细胞代谢产物中，才能发现新的药理学制剂非常有效，并且由于特异性而没有副作用。

唯一的问题是，如何以及在哪里寻找NRP？ 它们非常有效，因此细胞绝对不需要大量生产，并且它们的浓度可以忽略不计。 因此，化学提取方法的准确性较低，约为1％，试剂和时间成本很高。 下一个 它们不是用DNA编码的，这意味着在基因组解码过程中积累的所有数据库以及生物信息学和基因组学的所有方法也是无用的。 找到某物的唯一方法是通过物理方法，即质谱法。 此外，现代光谱仪中物质的检测水平非常高，以至于人们可以发现总量>〜800个分子（大摩尔范围或浓度）的微不足道的量$$ $ inline $ 10 ^ {-18} $ inline $ ）

”

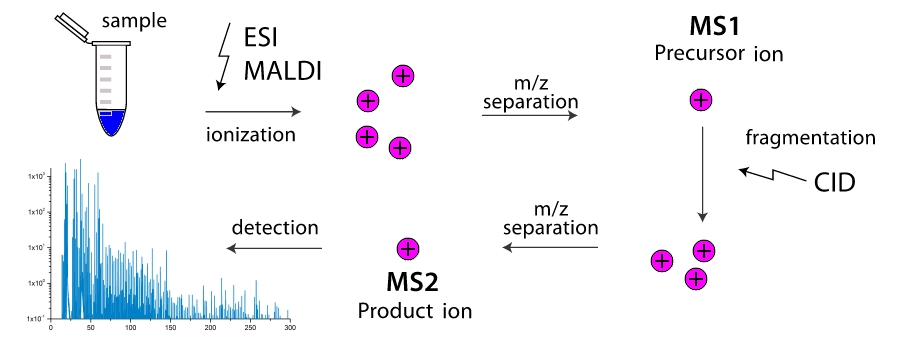
质谱仪如何工作？ 在设备的工作室中，分子被分解成碎片（更多的是由于彼此之间的碰撞，而很少是由于外部影响）。 这些碎片被电离，然后在外部电磁场中加速并分离。 分离是在检测器到达时发生的，或者是在磁场中旋转的角度发生的，因为碎片的质量较大且其电荷较低，因此更加笨拙。 因此，质谱仪“称量”了碎片的质量。 此外，可以通过重复过滤具有相同质量（更精确地说，具有一个值的片段）的段来“称重”$$ $内联$ m / z $内联$ ），并通过进一步分离将它们破碎。 两级质谱仪分布广泛，被称为串联质谱仪，多级质谱仪非常少见，简称为$$ $内联$ ms ^ n $内联$ 在哪里$$ $内联$ n $内联$ -阶段数。 在这里出现任务，如何仅知道任何分子的各种片段的质量，如何知道其结构？ 因此，我们分别讨论了线性和环状肽段的收费问题和环行问题。

我将以环肽为例，更详细地说明如何将恢复生物分子结构的任务减少到所指出的问题。



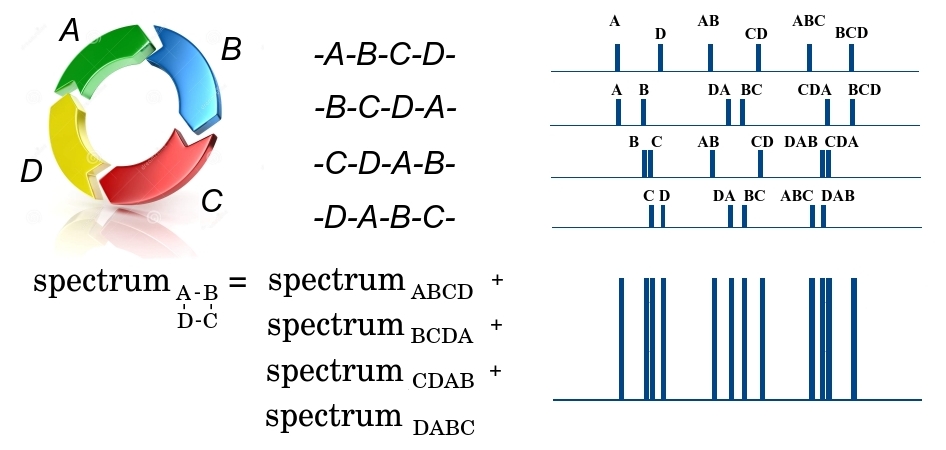
断裂第一阶段的环状肽ABCD可以通过DA键或AB，BC或CD在4个位置断裂，形成4种可能的线性肽-ABCD，BCDA，CDAB或DABC。 由于大量相同的肽通过光谱仪，因此输出处将具有所有4种类型的片段。 此外，我们注意到所有碎片都具有相同的质量，无法在第一阶段分离。 在第二阶段中，线性片段ABCD可以在三个位置断裂，形成具有不同质量A和BCD，AB和CD，ABC和D的较小片段，并形成相应的质谱图。 在该光谱中，片段质量沿x轴绘制，具有给定质量的小片段数量沿y轴绘制。 类似地，为剩余的三个BCDA，CDAB和DABC线性片段形成光谱。 由于所有4个大片段均进入第二阶段，因此将它们的所有光谱相加。 总计，结果是一些质量$$ $ inline $ \ {m_1 ^ {n_1}，m_2 ^ {n_2}，..，m_q ^ {n_q} \} $ inline $ 在哪里$$ $内联$ m_i $内联$ -一些质量，并且$$ $内联$ n_i $内联$ -重复的频率。 同时，由于不同的片段可以具有一个质量，因此我们不知道该质量属于哪个片段以及该片段是否唯一。 肽中的键彼此之间的距离越远，它们之间的肽片段的质量就越大。 也就是说，恢复环肽中元素的顺序的任务减少为绕道问题，其中集合中的元素$$ $内联$ X $内联$ 是肽中的键，以及众多元素$$ $内联$ \ Delta X $内联$ -键之间的碎片块。

预期存在多项式时间的算法来解决环城公路问题

从我的经验以及与尝试或确实做出了解决该问题的工作人员的交流中，我注意到绝大多数人试图在一般情况下或在较小范围内的整数数据（例如，（1， 50）。 两种选择都注定要失败。 对于一般情况，证明了在一维情况下解决环道问题的总数$$ $内联$ S_1（n）$内联$ 受价值限制（Lemke，2003年）

$$$$ display $$ e ^ {2 ^ {\ frac {\ ln n} {\ ln \ ln n} + o（1）}} \ leq S_1（n）\ leq \ frac {1} {2} n ^ {n-2} $$显示$$

这意味着渐近中存在指数级的解$$ $ inline $ n \ rightarrow \ infty $ inline $ 。 显然，如果解决方案的数量呈指数增长，那么接收它们的时间就不会增长得更慢。 即，对于一般情况，不可能获得多项式时间解。 至于窄范围内的整数数据，所有内容都可以通过实验进行验证，因为编写通过穷举搜索来寻找解决方案的代码并不难。 对于小$$ $内联$ n $内联$ 这样的代码不会花费很长时间。 此类代码的测试结果将表明，在此类数据条件下，任何一组的不同解决方案的总数$$ $内联$ \ Delta X $内联$ 已经很小$$ $内联$ n $内联$ 也急剧增长。

了解了这些事实之后，您可以放弃并放弃此任务。 我承认这是仍然认为环城公路问题尚未解决的原因之一。 但是，确实存在漏洞。 回想一下指数函数$$ $ inline $ e ^ {\ alpha x} $ inline $ 表现非常有趣。 最初，它的增长速度非常缓慢，在从$$ $ inline $ \ infty $ inline $ 到0，则它的增长越来越快。 但是，值越低$$ $内联$ \ alpha $内联$ 该值应该越大$$ $内联$ x $内联$ 这样函数的结果会超过某个设置值$$ $内联$ y = \ xi $内联$ 。 作为这样的值，选择数字很方便$$ $内联$ \ xi = 2 $内联$ ，在他之前唯一的解决方案，在他之后还有很多决定。 问题 有人检查过决定数量对输入的数据的依赖性吗？ 是的，我做到了。 克罗地亚女数学家塔玛拉·达基斯（Tamara Dakis，Dakic，2000年）撰写了一篇精彩的博士学位论文，她在其中确定了输入数据必须满足的条件才能在多项式时间内解决问题。 其中最重要的是解决方案的唯一性以及在输入数据集中没有重复项。$$ $内联$ \ Delta X $内联$ 。 她的博士学位论文水平很高。 不幸的是，这名学生只把自己限制在收费公路问题上，我坚信，如果她对高速公路过境问题产生了兴趣，那早就可以解决了。

获得具有多项式时间的算法来解决环城公路问题

可能会偶然发现可能建立所需算法的数据。 它花了更多的想法。 主要的想法来自观察（见上文），即环肽的光谱是单环断裂时形成的所有线性肽的光谱之和。 由于可以从任何此类线性肽段中还原肽段中的氨基酸序列，因此光谱中的总行数非常大（在$$ $内联$ n $内联$ 时代在哪里$$ $内联$ n $内联$ -肽中的氨基酸数量过多）。 问题仅在于应从谱图中排除哪些谱系，以免失去恢复序列的能力。 由于这两个任务（从质谱图和环带通道问题中还原环状肽序列）在数学上是同构的，因此还可以剔除许多任务$$ $内联$ \ Delta X $内联$ 。

细化操作$$ $内联$ \ Delta X $内联$ 使用集合的局部对称构造$$ $内联$ \ Delta X $内联$ （Fomin，2016a）。

• 对称化 第一个操作是选择集合中的任意元素$$ $ inline $ x _ {\ mu} \ in \ Delta X $ inline $ 并从中删除$$ $内联$ \ Delta X $内联$ 除相对于点具有对称对的元素外的所有元素$$ $ inline $ x _ {\ mu} / 2 $ inline $ 和$$ $ inline $（L + x _ {\ mu}）/ 2 $ inline $ 在哪里$$ $内联$ L $内联$ -圆周（我记得在环行公路的情况下，所有点都位于圆上）。
• 部分解卷积。 第二个操作使用关于解的猜测，即，属于该解的各个点的知识，即所谓的部分解。 在很多$$ $内联$ \ Delta X $内联$ 除满足条件的元素外，所有元素也都被删除-如果我们测量从测试点到部分解的所有点的距离，则所有获得的值都在$$ $内联$ \ Delta X $内联$ 。 我要澄清的是，如果至少不存在所获得的距离之一$$ $内联$ \ Delta X $内联$ 然后忽略这一点。

定理证明，这两个运算都使集合变稀疏$$ $内联$ \ Delta X $内联$ ，但它仍有足够的元素来还原解决方案$$ $内联$ X $内联$ 。 使用这些操作，使用c ++构建并实现了一种算法，以解决环城公路问题（Fomin，2016b）。 该算法与经典的回溯算法几乎没有什么不同（也就是说，我们尝试通过枚举可能的选项来构建解决方案，如果在构建过程中遇到错误，则返回该值）。 唯一的不同是缩小范围$$ $内联$ \ Delta X $内联$ 测试我们的选择就少得多了。

这是一个例子$$ $内联$ \ Delta X $内联$ 稀疏时。



对随机产生的长度为10的环肽进行了计算实验$$ $内联$ n $内联$ 10至1000个氨基酸（纵坐标为对数刻度）。 横坐标还以对数刻度显示通过各种操作变薄的集合中的元素数量$$ $内联$ \ Delta X $内联$ 单位$$ $内联$ n $内联$ 。 这样的表示绝对是不寻常的，因此我将在一个示例中解释它的读取方式。 我们看左图。 让肽有长度$$ $内联$ n = 100 $内联$ 。 对他来说，集合中元素的数量$$ $内联$ \ Delta X $内联$ 等于$$ $内联$ n ^ 2 = 10000 $内联$ （这是上方虚线上的一个点$$ $内联$ y = n ^ 2 $内联$ ） 从集合中删除后$$ $内联$ \ Delta X $内联$ 重复元素，元素数量$$ $内联$ \ Delta X $内联$ 减少到$$ $ inline $ n_D \大约n ^ {1.9} \大约6300 $ inline $ （带有圆圈的圆圈）。 对称化后，元素数量下降到$$ $ inline $ n_S \大约n ^ {1.75} \大约3100 $ inline $ （黑色圆圈），并在通过部分解卷积后$$ $ inline $ n_C \大约n ^ {1.35} \大约500 $ inline $ （十字架）。 合计，总集$$ $内联$ \ Delta X $内联$ 仅减少了20倍。 对于相同长度的肽，但在右图中，收缩来自$$ $内联$ n ^ 2 = 10000 $内联$ 之前$$ $ inline $ N_C \大约n \大约100 $ inline $ ，即100次。

请注意，执行左侧图的测试用例的生成是为了确保重复级别$$ $ inline $ k_ {dup} $ inline $ 在$$ $内联$ \ Delta X $内联$ 在0.1到0.3的范围内，对于右边-小于0.1。 重复级别定义为$$ $ inline $ k_ {dup} = 2- \ log {N_u} / \ log {n} $ inline $ 在哪里$$ $内联$ N_u $内联$ -集合中唯一元素的数量$$ $内联$ \ Delta X $内联$ 。 这样的定义给出了自然的结果：在集合中没有重复项$$ $内联$ \ Delta X $内联$ 它的力量相等$$ $内联$ N_u = n ^ 2 $内联$ 和$$ $ inline $ k_ {dup} = 0 $ inline $ 以最大可能的重复$$ $内联$ N_u = n $内联$ 和$$ $ inline $ k_ {dup} = 1 $ inline $ 。 我将稍后再讲如何如何提供不同级别的重复。 这些图表明，重复级别越低，清除越薄$$ $内联$ \ Delta X $内联$ 在$$ $ inline $ k_ {dup} <0.1 $ inline $ 细化的元素数$$ $内联$ \ Delta X $内联$ 一般达到极限$$ $ inline $ O（n ^ 2）\ rightarrow O（n）$ inline $ ，因为在抽取的集合中小于$$ $内联$ O（n）$内联$ 元素无法获得（操作存储了足够的元素以获取解决方案，其中$$ $内联$ n $内联$ 元素）。 缩小集合力量的事实$$ $内联$ \ Delta X $内联$ 降低到下限非常重要，正是他导致了获得解决方案的计算复杂性的巨大变化。

在将细化操作添加到回溯算法中并解决了环行问题之后，Tamara Dakis谈到了关于收费问题的完整模拟。 让我提醒你。 她说，对于收费公路问题，如果解是唯一的并且没有重复项，则可以在多项式时间内得到解。$$ $内联$ \ Delta X $内联$ 。 事实证明，完全没有重复是没有必要的（对于实际数据几乎是不可能的），它的级别将非常小就足够了。 下图显示了解决带状通道问题所需的时间，具体取决于肽的长度和重复序列的水平。$$ $内联$ \ Delta X $内联$ 。



在图中，横坐标和纵坐标均以对数标度给出。 这使您可以清楚地看到计数时间是否与序列长度有关$$ $内联$ T = f（n）$内联$ 指数（直线）或多项式（对数曲线）。 从图中可以看出，重复程度很低（右图），解决方案是在多项式时间内获得的。 好吧，更准确地说，解决方案是在二次时间内获得的。 当细化操作将集合的功效降低到下限时，会发生这种情况。$$ $ inline $ O（n ^ 2）\ rightarrow O（n）$ inline $ ，其中几乎没有剩下的要点，枚举选项变为单个时返回，本质上，算法不再对选项进行迭代，而是仅根据剩余的内容构造一个解决方案。

PS：嗯，我将揭示有关在不同重复级别生成集的最后一个秘密。 这是由于数据表示的准确性不同。 如果生成的数据精度较低（例如，四舍五入为整数），则重复级别将变得很高，大于0.3。如果生成的数据具有较高的准确性，例如最多3个小数位，则重复级别将急剧下降，小于0.1。最后是最重要的一句话。

对于真实数据，在测量精度不断提高的情况下，环带问题可以实时解决。


文学作品

1. Dakic，T.（2000）。关于收费公路问题。西蒙弗雷泽大学博士学位论文。
2. Fomin。 E.（2016a）从n ^ 2成对距离的n ^ 2个步骤中的n ^ 2个成对距离的多集重构点集的简单方法：I.理论。 J计算生物学。 2016，23（9）：769-75。
3. Fomin。E.（2016b）一种从n ^ 2成对距离的多集中以n ^ 2步的多集重构点集的简单方法：II。算法。J计算生物学。2016，23（12）：934-942。
4. Lemke，P.，Skiena，S.和Smith，W.（2003）。从点间距离重构集。离散和计算几何算法和组合，25：597-631。
5.Skiena，S.，Smith，W。和Lemke，P。（1990）。从点间距离重建集合。在第六届ACM计算几何专题研讨会论文集，第332–339页中。加州伯克利
6.张，Z。1982。部分摘要映射算法的指数示例。J.比较 生物学 1，235-240。