通过使用像素的示例实现k均值（k-means）算法

大家好！ 最近，有必要编写代码以使用k-means方法（英语k-means）实现图像分割。 好吧，Google要做的第一件事就是帮助。 我发现了很多信息，而且从数学的角度来看（那里各种各样的数学涂鸦，您都会明白那里写的是什么），以及英语Internet上的一些软件实现。 这些代码当然很漂亮-毫无疑问，但是这个想法的本质很难理解。 不知何故，那里一切都变得复杂，混乱，但是，用手，用手，您不会编写代码，您一无所知。 在本文中，我希望展示一种简单而有效的方法，但是，我希望可以理解这种出色算法的实现。 好吧，走吧！

那么，就我们的看法而言，聚类是什么？ 让我举个例子，假设有一张漂亮的照片，上面有您祖母的小屋里的花。



问题是：确定这张照片中的多少区域填充了几乎相同的颜色。 好吧，这一点也不困难：白色的花瓣-一个，黄色的中心-两个（我不是生物学家，我不知道它们的名字），三个绿色。 这些部分称为群集。 聚类是具有共同特征（颜色，位置等）的数据的组合。 确定任何数据的每个组成部分并将其放置在此类群集（节）中的过程称为群集。

聚类算法很多，但是最简单的是k-medium，稍后将进行讨论。 K-means是一种简单高效的算法，可使用软件方法轻松实现。 我们将在群集中分发的数据是像素。 如您所知，彩色像素具有三个成分-红色，绿色和蓝色。 强制使用这些组件并创建现有颜色的调色板。



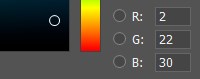
在计算机内存中，每个颜色分量都用0到255之间的数字表示。也就是说，结合红色，绿色和蓝色的不同值，我们会在屏幕上获得一个调色板。

以像素为例，我们实现了算法。 K均值是一种迭代算法，也就是说，在重复一些数学计算后，它将给出正确的结果。

演算法

1. 您需要事先知道需要多少个群集才能分发数据。 这是该方法的一个重大缺点，但是可以通过改进算法的实现来解决此问题，但是正如他们所说，这是完全不同的故事。
2. 我们需要选择集群的初始中心。 怎么了 是的。 怎么了 这样就可以将每个像素捕捉到群集的中心。 中心就像国王，周围聚集着他的主体-像素。 从中心到像素的“距离”决定了每个像素将服从的对象。
3. 我们计算从每个中心到每个像素的距离。 该距离被视为空间中点之间的欧几里得距离，在我们的示例中，被视为三个颜色分量之间的距离：

   $$$$ display $$ \ sqrt {（R_ {2} -R_ {1}）^ 2 +（G_ {2} -G_ {1}）^ 2 +（B_ {2} -B_ {1}）^ 2} 。$$显示$$

   我们计算从第一个像素到每个中心的距离，并确定该像素与中心之间的最小距离。 对于距离最小的中心，我们重新计算坐标，将其作为对象的像素各部分（国王和像素）之间的算术平均值。 我们的中心根据计算在空间上移动。
4. 重新计算所有中心之后，我们将像素分布到群集中，比较每个像素到中心的距离。 像素放置在群集中，该群集的中心比其他中心更近。
5. 只要像素保留在相同的簇中，一切都会重新开始。 通常，这可能不会发生，因为随着大量数据的出现，中心将以较小的半径移动，并且沿群集边缘的像素将跳入一个或另一个群集中。 为此，请确定最大迭代次数。

实作

我将用C ++实现该项目。 第一个文件是“ k_means.h”，在其中定义了主要的数据类型，常量和主要的工作类“ K_means”。
为了表征每个像素，创建一个由三个像素组成的结构，为此，我选择了double类型以进行更精确的计算，还定义了一些常量以使程序可以工作：

const int KK = 10; //  const int max_iterations = 100; //   typedef struct { double r; double g; double b; } rgb; 

K_means类本身：

 class K_means { private: std::vector<rgb> pixcel; int q_klaster; int k_pixcel; std::vector<rgb> centr; void identify_centers(); inline double compute(rgb k1, rgb k2) { return sqrt(pow((k1.r - k2.r),2) + pow((k1.g - k2.g), 2) + pow((k1.b - k2.b), 2)); } inline double compute_s(double a, double b) { return (a + b) / 2; }; public: K_means() : q_klaster(0), k_pixcel(0) {}; K_means(int n, rgb *mas, int n_klaster); K_means(int n_klaster, std::istream & os); void clustering(std::ostream & os); void print()const; ~K_means(); friend std::ostream & operator<<(std::ostream & os, const K_means & k); }; 

让我们看一下该类的组件：

vectorpixcel-像素向量；
q_klaster-集群数；
k_pixcel-像素数；
vectorcentr-聚类中心的向量，其中的元素数量由q_klaster确定；
identify_centers（）-一种在输入像素中随机选择初始中心的方法；
compute（）和compute_s（）是分别用于计算像素之间的距离和重新计算中心的内置方法；
三个构造函数：默认情况下是第一个，第二个是用于初始化数组中的像素，第三个是用于初始化文本文件中的像素（在我的实现中，文件首先被意外地填充了数据，然后从该文件中读取了像素以使程序正常工作，为什么不直接将其放入向量中-就我而言就需要）;
聚类（std :: ostream＆os）-聚类方法；
方法和重载输出语句以发布结果。

方法实现：

 void K_means::identify_centers() { srand((unsigned)time(NULL)); rgb temp; rgb *mas = new rgb[q_klaster]; for (int i = 0; i < q_klaster; i++) { temp = pixcel[0 + rand() % k_pixcel]; for (int j = i; j < q_klaster; j++) { if (temp.r != mas[j].r && temp.g != mas[j].g && temp.b != mas[j].b) { mas[j] = temp; } else { i--; break; } } } for (int i = 0; i < q_klaster; i++) { centr.push_back(mas[i]); } delete []mas; } 

这是一种选择初始聚类中心并将其添加到中心向量的方法。 在这些情况下，将进行检查以重复中心并替换它们。

 K_means::K_means(int n, rgb * mas, int n_klaster) { for (int i = 0; i < n; i++) { pixcel.push_back(*(mas + i)); } q_klaster = n_klaster; k_pixcel = n; identify_centers(); } 

用于初始化数组中像素的构造函数实现。

 K_means::K_means(int n_klaster, std::istream & os) : q_klaster(n_klaster) { rgb temp; while (os >> temp.r && os >> temp.g && os >> temp.b) { pixcel.push_back(temp); } k_pixcel = pixcel.size(); identify_centers(); } 

我们将输入对象传递给此构造函数，以便能够从文件和控制台中输入数据。

 void K_means::clustering(std::ostream & os) { os << "\n\n :" << std::endl; /*             :        ,    -  ,    ,   ,        .*/ std::vector<int> check_1(k_pixcel, -1); std::vector<int> check_2(k_pixcel, -2); int iter = 0; /* .*/ while(true) { os << "\n\n----------------  №" << iter << " ----------------\n\n"; { for (int j = 0; j < k_pixcel; j++) { double *mas = new double[q_klaster]; /*  :          .      ,   .*/ for (int i = 0; i < q_klaster; i++) { *(mas + i) = compute(pixcel[j], centr[i]); os << "   " << j << "   #" << i << ": " << *(mas + i) << std::endl; } /*     m_k      .*/ double min_dist = *mas; int m_k = 0; for (int i = 0; i < q_klaster; i++) { if (min_dist > *(mas + i)) { min_dist = *(mas + i); m_k = i; } } os << "    #" << m_k << std::endl; os << "  #" << m_k << ": "; centr[m_k].r = compute_s(pixcel[j].r, centr[m_k].r); centr[m_k].g = compute_s(pixcel[j].g, centr[m_k].g); centr[m_k].b = compute_s(pixcel[j].b, centr[m_k].b); os << centr[m_k].r << " " << centr[m_k].g << " " << centr[m_k].b << std::endl; delete[] mas; } /*   .*/ int *mass = new int[k_pixcel]; os << "\n  : "<< std::endl; for (int k = 0; k < k_pixcel; k++) { double *mas = new double[q_klaster]; /*    .*/ for (int i = 0; i < q_klaster; i++) { *(mas + i) = compute(pixcel[k], centr[i]); os << "   №" << k << "   #" << i << ": " << *(mas + i) << std::endl; } /*  .*/ double min_dist = *mas; int m_k = 0; for (int i = 0; i < q_klaster; i++) { if (min_dist > *(mas + i)) { min_dist = *(mas + i); m_k = i; } } mass[k] = m_k; os << " №" << k << "     #" << m_k << std::endl; } /*            .*/ os << "\n    : \n"; for (int i = 0; i < k_pixcel; i++) { os << mass[i] << " "; check_1[i] = *(mass + i); } os << std::endl << std::endl; os << " : " << std::endl; int itr = KK + 1; for (int i = 0; i < q_klaster; i++) { os << " #" << i << std::endl; for (int j = 0; j < k_pixcel; j++) { if (mass[j] == i) { os << pixcel[j].r << " " << pixcel[j].g << " " << pixcel[j].b << std::endl; mass[j] = ++itr; } } } delete[] mass; /*    .*/ os << " : \n" ; for (int i = 0; i < q_klaster; i++) { os << centr[i].r << " " << centr[i].g << " " << centr[i].b << " - #" << i << std::endl; } } /*         –  .*/ iter++; if (check_1 == check_2 || iter >= max_iterations) { break; } check_2 = check_1; } os << "\n\n ." << std::endl; } 

聚类的主要方法。

 std::ostream & operator<<(std::ostream & os, const K_means & k) { os << " : " << std::endl; for (int i = 0; i < k.k_pixcel; i++) { os << k.pixcel[i].r << " " << k.pixcel[i].g << " " << k.pixcel[i].b << " - №" << i << std::endl; } os << std::endl << "   : " << std::endl; for (int i = 0; i < k.q_klaster; i++) { os << k.centr[i].r << " " << k.centr[i].g << " " << k.centr[i].b << " - #" << i << std::endl; } os << "\n : " << k.q_klaster << std::endl; os << " : " << k.k_pixcel << std::endl; return os; } 

初始数据的输出。

输出例子

该示例预先计划好，专门选择了像素进行演示。 两次迭代足以使程序将数据分组为三个群集。 查看最后两个迭代的中心，您会发现它们实际上保持不变。

更有趣的是随机生成像素的情况。 生成了50个需要划分为10个类的点后，我得到了5次迭代。 生成了50个需要划分为3个类的点后，我得到了所有100个最大允许的迭代。 您可能会注意到，群集越多，程序越容易找到最相似的像素并将它们组合成较小的组，反之亦然-如果群集很少且有很多点，则算法通常仅在超过最大迭代次数时结束，因为某些像素不断跳跃从一个集群到另一个集群。 但是，大部分仍完全由其集群确定。

好了，现在让我们检查聚类的结果。 从每10个群集50个点的示例中得出一些群集的结果，我将这些数据的结果驱动到Illustrator中，结果是这样的：



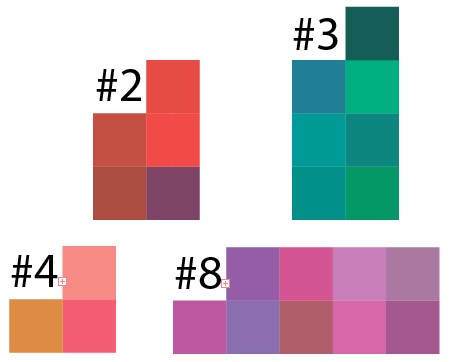
可以看出，在每个簇中，任何颜色的阴影都占主导地位，在这里您需要了解像素是随机选择的，现实生活中这种图像的类似物是某种图片，意外地在其上喷涂了所有颜色，并且很难选择相似颜色的区域。

假设我们有这样一张照片。 我们可以将一个岛定义为一个群集，但是随着增加，我们看到它由不同的绿色阴影组成。



这是集群8，但在较小的版本中，结果类似：



该程序的完整版本可以在我的GitHub上查看。