不久前,Habr 翻译了一篇文章 , 内容涉及如何使用代数数据类型以确保不正确的状态是不可表达的。 今天,我们研究一种表达这种无法表达的方式的方式,该方式稍微更笼统,更可扩展且更安全,Haskell将在此方面为我们提供帮助。
简而言之,该文章讨论了一个具有邮件地址和电子邮件地址的实体,以及附加条件,即必须至少有一个这些地址。 建议如何在类型级别上表达此条件? 建议写以下地址:
type ContactInfo = | EmailOnly of EmailContactInfo | PostOnly of PostalContactInfo | EmailAndPost of EmailContactInfo * PostalContactInfo
这种方法有什么问题?
最明显的(在该文章的评论中多次提到)是这种方法根本无法扩展。 想象一下,我们没有两种类型的地址,而是三个或五个,正确性条件看起来像“必须有一个邮寄地址,或者既有电子邮件地址又有办公地址,并且不应有多个相同类型的地址”。 那些希望的人可以编写适当的类型作为自测练习。 当关于不存在重复项的条件从TOR中消失时,带有星号的任务是重写此类型。
分享到
如何解决这个问题? 让我们尝试幻想。 首先,我们分解并分离地址类(例如,办公室中的邮件/电子邮件/服务台号码)和与该类相对应的内容:
data AddrType = Post | Email | Office
我们不会考虑该内容,因为在地址列表的有效性方面,它与内容无关。
如果我们在某些普通的OOP语言的构造函数的运行时中检查了相应的条件,那么我们将编写一个类似
valid :: [AddrType] -> Bool valid xs = let hasNoDups = nub xs == xs
如果返回False ,将引发一些执行。
在编译时,是否可以在计时器的帮助下检查类似情况? 事实证明,是的,如果语言的类型系统足够表达,我们可以,在本文的其余部分,我们将采用这种方法。
在这里,依赖类型将对我们有很大帮助,由于在Haskell中编写经过验证的代码的最充分方法是首先在Agde或Idris中编写代码,因此我们将换鞋并在Idris中编写代码。 idris语法非常接近Haskell:例如,使用上述功能,您只需稍微更改签名即可:
valid : List AddrType -> Bool
现在请记住,除了地址类别外,我们还需要它们的内容,并将字段对地址类别的依赖性编码为GADT:
data AddrFields : AddrType -> Type where PostFields : (city : String) -> (street : String) -> AddrFields Post EmailFields : (email : String) -> AddrFields Email OfficeFields : (floor : Int) -> (desk : Nat) -> AddrFields Office
也就是说,如果给我们一个类型为AddrFields t的fields值,那么我们知道t是某个AddrType AddrType并且该fields包含与该特定类相对应的一组字段。
关于这篇文章这不是最安全的类型编码,因为GADT不必是内射的,并且声明三个单独的数据类型PostFields , EmailFields , OfficeFields并编写函数会更正确
addrFields : AddrType -> Type addrFields Post = PostFields addrFields Email = EmailFields addrFields Office = OfficeFields
但这太多了,对于原型并没有太大的收获,为此,在Haskell中仍然有更加简洁和令人愉悦的机制。
此模型的整个地址是什么? 这是一对地址类和相应的字段:
Addr : Type Addr = (t : AddrType ** AddrFields t)
类型理论的拥护者会说这是一个与存在有关的类型:如果我们给定了类型Addr值,那么这意味着存在类型AddrType的值t和一组对应的AddrFields t字段。 当然,不同类别的地址是同一类型:
someEmailAddr : Addr someEmailAddr = (Email ** EmailFields "that@feel.bro") someOfficeAddr : Addr someOfficeAddr = (Office ** OfficeFields (-2) 762)
此外,如果将EmailFields给我们,那么唯一合适的地址类别是Email ,因此您可以省略它,计时器将自己打印它:
someEmailAddr : Addr someEmailAddr = (_ ** EmailFields "that@feel.bro") someOfficeAddr : Addr someOfficeAddr = (_ ** OfficeFields (-2) 762)
我们编写了一个辅助函数,该函数提供了地址列表中相应的地址类列表,并立即将其泛化为可在任意函子上工作:
types : Functor f => f Addr -> f AddrType types = map fst
在这里,存在的Addr类型的行为就像一对熟悉的夫妇:特别是,您可以要求其第一个组件AddrType (带有星号的任务:为什么我不能要求第二个组件?)。
升起
现在我们继续讲故事的关键部分。 因此,我们有一个List Addr地址List Addr和一些valid : List AddrType -> Bool谓词valid : List AddrType -> Bool ,我们要保证在类型级别上对此列表的执行。 我们如何结合它们? 当然是另一种类型!
data ValidatedAddrList : List Addr -> Type where MkValidatedAddrList : (lst : List Addr) -> (prf : valid (types lst) = True) -> ValidatedAddrList lst
现在,我们将分析在这里写的内容。
data ValidatedAddrList : List Addr -> Type where表示类型ValidatedAddrList实际上是由地址列表参数化的。
让我们看一下这种类型的唯一MkValidatedAddrList构造函数的签名: (lst : List Addr) -> (prf : valid (types lst) = True) -> ValidatedAddrList lst 。 也就是说,它需要一些lst地址列表和另一个valid (types lst) = True prf参数。 这种类型是什么意思? 因此,这意味着=左边的值等于=右边的值,即valid (types lst)实际上为True。
如何运作? 签名=看起来像(x : A) -> (y : B) -> Type 。 也就是说, =取两个任意值x和y (甚至可能具有不同的A和B类型,这意味着idris中的不等式是异质的,从类型理论的角度来看它有点模棱两可,但这是另一个讨论的主题)。 那么什么证明了平等呢? 并且由于唯一的构造函数= Refl具有几乎 (x : A) -> x = x的签名。 也就是说,如果我们具有类型x = y的值,那么我们知道它是使用Refl构建的(因为没有其他构造函数),这意味着x实际上等于y 。
请注意,这就是为什么在Haskell中我们总是充其量只能冒充我们正在证明的东西,因为Haskell具有undefined ,可以居住任何类型的东西,因此上述参数在那里不起作用:对于任何x , y x = y类型项x = y可以通过undefined (或通过无限递归来创建,也就是说,就类型理论而言,基本上是相同的)。
我们还注意到,这里的相等并不是从Haskell的Eq或C ++中的任何operator==的意义出发,而是要严格得多:结构化的,简化地表示这两个值具有相同的形式 。 也就是说,如此欺骗他根本行不通。 但是,传统上,平等问题是由单独的条款提出的。
为了巩固我们对相等性的理解,我们为valid功能编写了单元测试:
testPostValid : valid [Post] = True testPostValid = Refl testEmptyInvalid : valid [] = False testEmptyInvalid = Refl testDupsInvalid : valid [Post, Post] = False testDupsInvalid = Refl testPostEmailValid : valid [Post, Email] = True testPostEmailValid = Refl
这些测试很好,因为您甚至不需要运行它们,taypcher检查它们就足够了。 确实,例如,在它们的第一个中,让我们用False替换True ,然后看看会发生什么:
testPostValid : valid [Post] = False testPostValid = Refl
Typsekher发誓

如预期的那样。 太好了
简化
现在,让我们重构一下ValidatedAddrList 。
首先,将某个值与True进行比较的模式非常普遍, So在idris中有一个特殊的类型So :您可以将So x用作x = True的同义词。 让我们修复ValidatedAddrList的定义:
data ValidatedAddrList : List Addr -> Type where MkValidatedAddrList : (lst : List Addr) -> (prf : So (valid $ types lst)) -> ValidatedAddrList lst
另外, So具有方便的辅助功能choose ,从本质上将检查提高到类型的水平:
> :doc choose Data.So.choose : (b : Bool) -> Either (So b) (So (not b)) Perform a case analysis on a Boolean, providing clients with a So proof
当我们编写修改此类型的函数时,这对我们很有用。
其次,有时(尤其是在交互式开发中)idris可以自行找到合适的prf值。 为了在这种情况下不必手工构建,有相应的语法糖:
data ValidatedAddrList : List Addr -> Type where MkValidatedAddrList : (lst : List Addr) -> {auto prf : So (valid $ types lst)} -> ValidatedAddrList lst
大括号表示这是idris将尝试脱离上下文的隐式参数,而auto表示他还将尝试自行构造它。
那么,这个新的ValidatedAddrList给我们带来了什么? 并给出了这样的推理链:令val为ValidatedAddrList lst类型的值。 这意味着lst是一个地址列表,此外, val是使用MkValidatedAddrList构造函数创建的,我们将这个lst和另一个So (valid $ types lst)类型的prf值So (valid $ types lst)传递给了val ,该值几乎是valid (types lst) = True 。 因此,我们可以构建prf ,实际上,我们需要证明这种平等成立。
最美丽的是,这一切都由一名tympher检查。 是的,有效性检查必须在运行时进行(因为可以从文件或网络中读取地址),但是计时器将确保完成此检查:没有它,就无法创建ValidatedAddrList 。 至少在idris中。 Has,在Haskell。
插入
要验证验证的必然性,请尝试编写将地址添加到列表的函数。 第一次尝试:
insert : (addr : Addr) -> ValidatedAddrList lst -> ValidatedAddrList (addr :: lst) insert addr (MkValidatedAddrList lst) = MkValidatedAddrList (addr :: lst)
不,错字检查器会在手指上显示(尽管不是很可读,但valid的成本太复杂了):
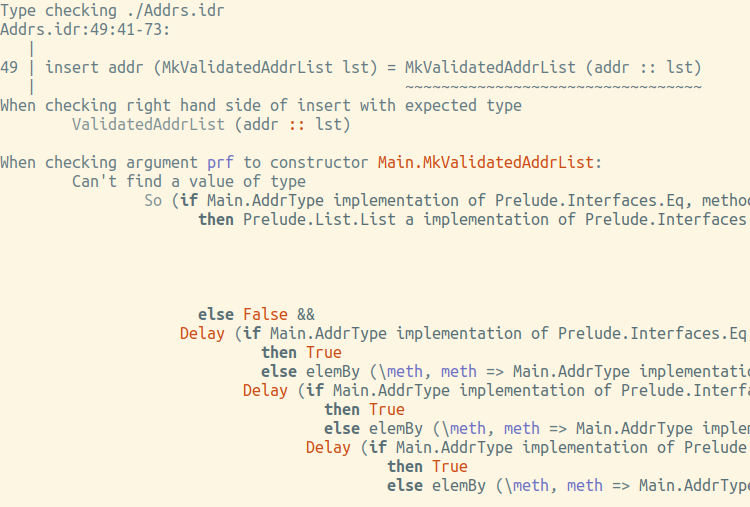
我们如何获得此So的副本? 除了上述choose 。 第二次尝试:
insert : (addr : Addr) -> ValidatedAddrList lst -> ValidatedAddrList (addr :: lst) insert addr (MkValidatedAddrList lst) = case choose (valid $ types (addr :: lst)) of Left l => MkValidatedAddrList (addr :: lst) Right r => ?rhs
它几乎是typechetsya。 “几乎”是因为不清楚用什么代替rhs 。 而是很清楚:在这种情况下,该函数必须以某种方式报告错误。 因此,您需要更改签名并包装返回值,例如在Maybe :
insert : (addr : Addr) -> ValidatedAddrList lst -> Maybe (ValidatedAddrList (addr :: lst)) insert addr (MkValidatedAddrList lst) = case choose (valid $ types (addr :: lst)) of Left l => Just $ MkValidatedAddrList (addr :: lst) Right r => Nothing
这是平铺的,并且可以正常工作。
但是现在出现了以下不是很明显的问题,实际上是原始文章中的问题。 此函数的类型不会停止编写这样的实现:
insert : (addr : Addr) -> ValidatedAddrList lst -> Maybe (ValidatedAddrList (addr :: lst)) insert addr (MkValidatedAddrList lst) = Nothing
也就是说,我们总是说我们无法建立新的地址列表。 Typhechaetsya? 是的 对吗 好吧,几乎没有。 可以避免吗?
事实证明这是有可能的,为此我们拥有所有必要的工具。 如果成功, insert返回ValidatedAddrList ,其中包含非常成功的证据。 因此,添加优雅的对称性,并要求函数还返回失败证明!
insert : (addr : Addr) -> ValidatedAddrList lst -> Either (So (not $ valid $ types (addr :: lst))) (ValidatedAddrList (addr :: lst)) insert addr (MkValidatedAddrList lst) = case choose (valid $ types (addr :: lst)) of Left l => Right $ MkValidatedAddrList (addr :: lst) Right r => Left r
现在,我们不能只接受并始终返回Nothing 。
您可以对地址删除功能等执行相同的操作。
让我们看看现在一切看起来如何。
让我们尝试创建一个空的地址列表:

这是不可能的,空列表无效。
只是一个邮寄地址列表呢?

好的,让我们尝试将邮寄地址插入已经具有邮寄地址的列表中:

让我们尝试插入电子邮件:
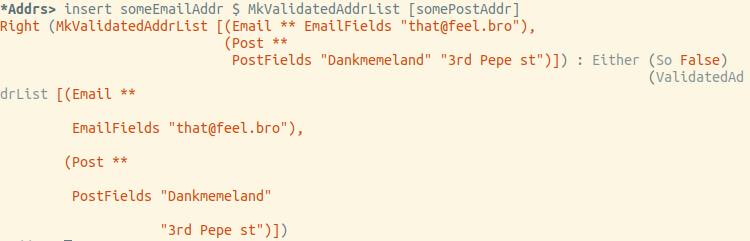
最后,一切都按预期进行。
ew 我以为会是三行,但结果更长了一点。 因此,要探索在Haskell中可以走多远,我们将在下一篇文章中。 在此期间,
思考
最终,与我们一开始就提到的文章相比,这种决定的利润是什么?
- 同样,它具有更大的可伸缩性。 复杂的验证功能更易于编写。
- 它更孤立。 客户代码不必知道验证功能的内容,而原始文章中的
ContactInfo表单则要求将其绑定。 - 验证逻辑是以普通的和熟悉的函数的形式编写的,因此可以通过仔细阅读立即进行检查,并通过编译时测试对其进行测试,而不用从表示已验证结果的数据类型中得出验证的含义。
- 可以更准确地指定与我们感兴趣的数据类型一起使用的功能的行为,尤其是在无法通过测试的情况下。 例如,写入的结果是根本不可能正确写入的。 同样,可以编写
insertOrReplace , insertOrIgnore之类的东西,其行为在类型中完全指定。
与像这样的OOP解决方案相比,利润是多少?
class ValidatedAddrListClass { public: ValidatedAddrListClass(std::vector<Addr> addrs) { if (!valid(addrs)) throw ValidationError {}; } };
- 该代码更加模块化和安全。 在上述情况下,检查是一次检查的操作 ,后来他们忘记了。 一切都基于诚实和理解,即如果您具有
ValidatedAddrListClass ,则其实现曾经在此处进行过检查。 该类检查的事实不能作为特定值来挑选。 对于某种类型的值,可以在程序的不同部分之间传递该值,用于构建更复杂的值(例如,再次拒绝此检查),进行调查(请参阅下一段),并且通常与我们以前做的一样与价值观。 - 此类检查可用于(相关的)模式匹配。 的确,在此函数
valid的情况下以及在idris的情况下都不是,这很麻烦,idris则很沉闷,因此可以从valid结构中提取对模式有用的信息。 尽管如此, valid可以用稍微友好的模式匹配样式进行重写,但这超出了本文的范围,并且通常本身并不琐碎。
缺点是什么?
我只看到一个严重的基本缺陷: valid太愚蠢了。 它仅返回一点信息-数据是否通过验证。 对于更智能的类型,我们可以实现一些更有趣的事情。
例如,想象一下地址唯一性的要求已经从传统知识中消失了。 在这种情况下,很明显在现有地址列表中添加新地址不会使列表无效,因此我们可以通过编写类型为So (valid $ types lst) -> So (valid $ types $ addr :: lst)类型的函数来证明该定理 。 So (valid $ types lst) -> So (valid $ types $ addr :: lst) ,并使用它来编写始终成功的类型安全
insert : (addr : Addr) -> ValidatedAddrList lst -> ValidatedAddrList (addr :: lst)
但是,可惜,定理如递归和归纳法,而且我们的问题没有任何优雅的归纳结构,因此,在我看来,具有Oak布尔valid的代码也不错。