在本文中,我们将基于结构建模的标准库(不使用现成的模糊调节块库)创建控制器模型。
作为控制对象,V.I。的教科书中的燃气涡轮发动机的模型。 Gosteva“自动控制系统中的模糊调节器”
让我们与PID和SDA调节器进行比较。
问题陈述
燃气涡轮发动机(燃气涡轮发动机)和涡轮喷气发动机(涡轮喷气发动机)之间的区别在于,在燃气涡轮发动机中,所有能量都通过轴除去。 在涡轮喷气发动机中,能量以射流的形式释放。
燃气涡轮发动机(GTE)广泛用于天然气和航空工业,它们是天然气抽油机和飞机发电厂的基础,在高峰和移动发电厂的工业用电动涡轮发电机的驱动器中,在船舶发电厂和其他需要开发大型单机容量的工业设施中(从1到25 MW)在一个单元中,具有最小的重量和尺寸。
燃气涡轮发动机在运行过程中对它们的可靠性,能效,安全性和环境友好性提出了一系列要求。 除了这些要求之外,还涉及与设备启动相关的瞬变质量要求,所选负载(功率)的急剧变化。 在许多方面,满足这些要求取决于燃气涡轮发动机的自动控制系统(ACS)。
工业上使用的典型燃气涡轮发动机是涡轮轴发动机,其电路如图1所示。
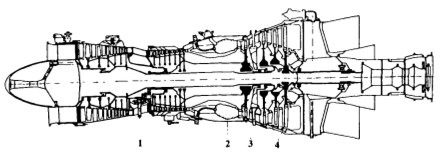
图1.典型的工业燃气涡轮发动机的示意图:
1-压缩机 2-燃烧室; 3-压缩机涡轮; 4-动力涡轮。
发动机是旋转式机械,其中空气在压缩机1中被压缩,供应给空气的燃料在燃烧室2中燃烧,部分能量来自压缩机3涡轮机中的热气,被压缩机1驱动器消耗,动力涡轮机中的4种气体消耗扩大消费者从引擎获取的动力。
在绝大多数燃气涡轮发动机中,转子速度是受控量。 作为ACS中的控制因素,转子转速n被用作燃烧室中的燃料消耗量GT。 在不同的运行模式下以及在各种外部条件下,发动机参数都会发生显着变化。
将燃气涡轮发动机(GTE)作为非平稳控制对象,其转子转速为n控制变量,而燃油消耗量G T为控制行为。 线性化涡轮力矩-M T和压缩机力矩-M K对转子速度的依赖关系,并且不考虑发动机在特定运行模式下的热和质量容量的影响,请写下发动机传递函数,如下所示:
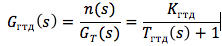
增益和时间常数定义为:
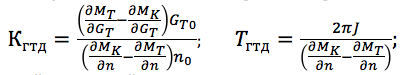
此外,输入和输出信号以相对于稳态的无量纲偏差记录(n =Δn/ n 0 ; G T =ΔG/ G TO ,其中针对特定的发动机运行模式选择参数的基本值,例如额定或最大)。 在不同的运行模式下以及在各种外部条件下,发动机的增益和时间常数会发生显着变化,因此,对于每种模式,必须确定其自身的K GTD和T GTD值 。
注意,在对象参数变化相当缓慢的情况下,通过“冻结”系数的方法获得了用于诸如燃气涡轮发动机的不稳定控制对象的燃气涡轮发动机的传递函数G。
用于自动控制发动机转子速度的模拟机电系统的框图如图2所示。
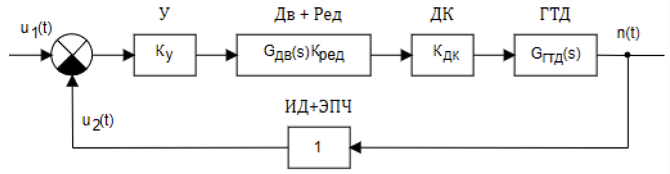
图2.模拟SAR GTE的框图
旋转频率由电压u 1 (t)设置,并由脉冲ID传感器改变,该脉冲ID传感器的输出信号的频率由以下表达式确定:
f = kmn,其中n是发动机转数,m是齿轮齿数,k是齿轮比。 使用EPC的电子变频器从ID输出获取的交流电压被转换为信号u2(t),其值与发动机转数-n成正比。 将电压u2(t)与参考电压和误差信号进行比较,然后将放大器U提供给两相异步电动机Dv,该电动机通过齿轮箱Red调节节气门DK,从而改变进入燃气轮机发动机的燃料流量。 脉冲传感器和电子变频器可以通过传递函数等于1的比例链接来描述。 在这种情况下,系统本身只有一个反馈。
将放大器,感应电动机,节气门,燃气轮机单元和频率传感器与电子变频器作为公共控制对象的串联连接,并使用数字模糊调节器,可以将图2的整个框图简化为图3的框图。链接的传递函数被减小为公共传递函数G 0 (s)。
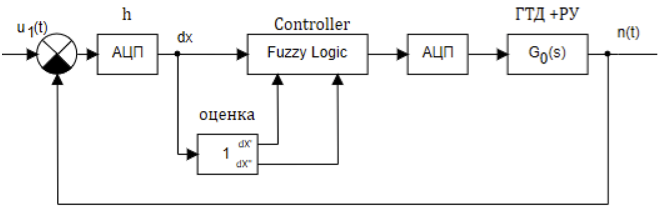
图3.具有模糊控制器的控制系统的结构。
通用传递函数G0(s)可以写为:
G 0 (s)= G (s)K 编辑 G (s)=α[s(s + a)(s + b)] -1 ,其中
α=abKK 编辑 K ,
a = 1 / T DW ,
b = 1 / T GTE
例如,我们假设传递函数对运行时间的依赖性为以下值:
T GTD (t)= 0.9849-0.1188×t + 0.0063×t 2-0.00012×t 3 ;
α(t)= 16.5475-4.4469×t + 0.4843×t 2-0.02315×t 3 + 0.0004×t 4 ;
T DW = 0.35 s。
在控制系统的研究中,我们假设改变燃气涡轮发动机转子转速的给定功能由输入电压u(t)设定
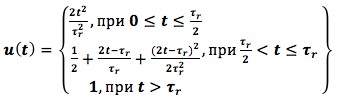
其中τr是发动机的加速时间。 我们取τr = 6秒。
创建动态模型
图4给出了引擎的简化模型。在该模型中,我们使用了典型模块的可变参数,这些参数在上面给出的相关性的仿真过程中会发生变化。
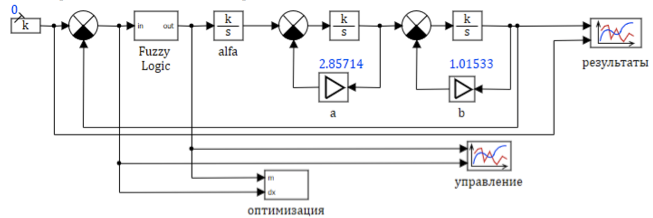
图4.燃气涡轮发动机模型的结构图
al,a,b放大器的系数是使用脚本语言计算的,程序文本如下:
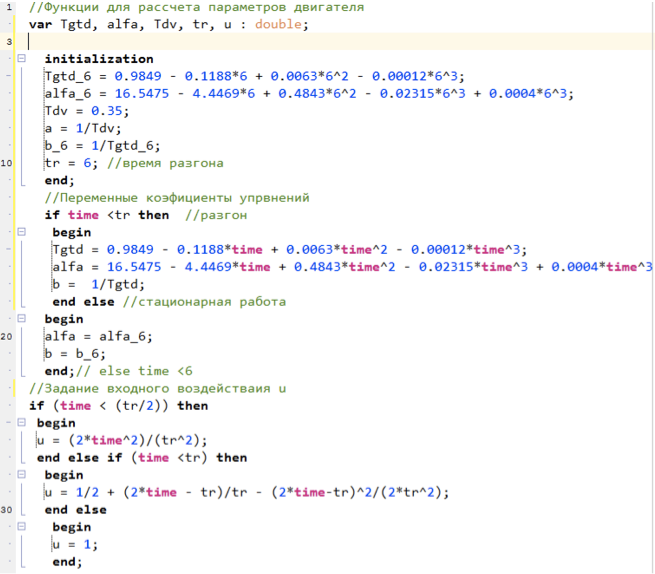
图5.用于计算模型参数的脚本。
模糊逻辑控制旋钮
控制调节器接受设定值和从模型获得的值之间的不匹配输入,并且必须计算控制动作。
让我们尝试仅使用数学上标准的结构建模块,而不使用专门的库,基于模糊逻辑组装控制器。
基于模糊逻辑的控制原理的描述可以在中心的上一篇文章中找到,也可以在此处创建专门的块库的描述中找到 (小心,亵渎)。
任何基于模糊逻辑的控制器都执行以下转换序列:
- 输入变量的阶段化。 变量的值由一组术语代替。
- 激活结论的模糊逻辑规则。
- 每个语言变量的结论积累。
- 消除输出变量的模糊化。
为了控制引擎,我们将使用三个连续变量,它们基于一个信号进行计算:
- 偏差
- 导数偏差(变化率偏差);
- 偏差的二阶导数(偏差变化的加速度)。
计算方案如图6所示:
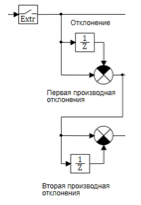
图6.一阶和二阶导数偏差的计算。
外推器块以0.01秒的周期对进入控制器的信号进行量化。 一阶和二阶导数使用差异公式计算:
 其中:
其中:
u(t)是时间t的当前偏差;
u(t-Δt)是时间t-Δt的偏差;
u'(t)是时间t时偏差的导数的当前值;
u'(t-Δt)是时间t-Δt时偏差的导数的值;
u''(t)是时刻t的偏差的二阶导数的当前值;
u''(t-Δt)是时间t-Δt时偏差的二阶导数的值;
Δt是量化周期。
在比较单元中执行Δt除法。
作为此块的结果,创建了三个语言变量:偏差,第一偏差变量,第二偏差变量。
为了解决模糊控制问题,我们将对每个语言变量仅使用两个术语。
偏差- 更少,更多;
偏差的一阶导数在减小,在增加;
偏差的二阶导数- 减速,加速。
为了计算每个项的隶属函数μ的值,我们使用具有饱和度的线性函数。 当输入值最小时,该术语的功能大于0,而在输入值最大时大于1。 少了一个术语,当变量等于最小值时,此函数取值1;当变量最大时,取0。 (见图7)
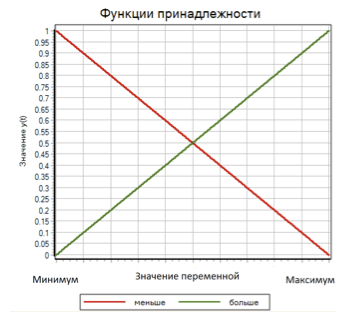
图7.术语的会员功能越来越少。
因此,对于三个输入变量(偏差,偏差的一阶导数,偏差的二阶导数)中的每一个,出现越来越多的两个项,隶属函数μi的值根据输入值从0线性变化到1变量。
作为输出语言变量,我们使用输出效果,该效果也只有两个术语要减少和增加。
从图的模型图。 从图4可以明显看出,如果偏差小于0,则该值大于指定值,需要减小。 如果偏差大于0,则功能小于指定的功能,需要增加。
这两个术语的逻辑规则如下所示:
- 如果小于 ,则减小并减慢 => 减小。
- 如果更多并增加并加速 => 增加。
为了激活模糊推理规则,我们对模糊和算子使用最小函数。 输出函数项的隶属函数的值由以下公式计算:
μ
减小 = MIN(μ
减小 ,μ
减小 ,μ
减慢 )
μ
增加 = MIN(μ
更多 ,μ
增加 ,μ
加速 )
为了确保将术语转换为特定的影响值(累积和脱硝),我们使用Tsukamoto算法作为这些点的重心。
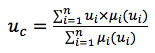 在哪里
在哪里
u c是结果函数;
u i是第i项的函数值;
μi是该函数项的隶属函数的值。
在我们的例子中,两个项的结果函数由以下公式计算:
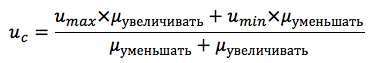
模糊推理算法的一般方案如图8所示:
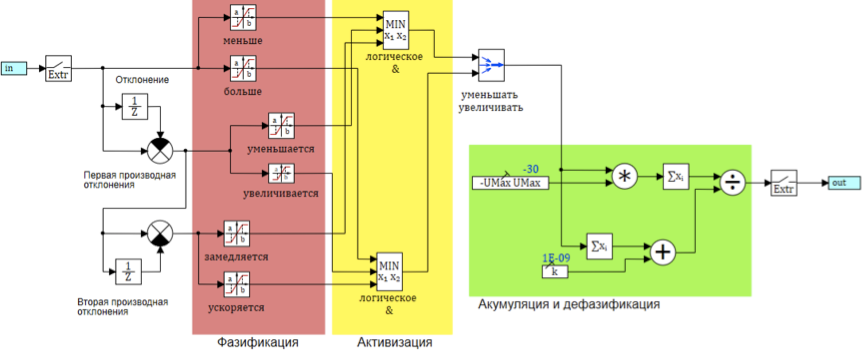
图8.模糊推理算法的方案
为了使该算法起作用,我们必须为三个语言变量(偏差,偏差的一阶导数,偏差的二阶导数)的6个项设置最小值和最大值。 为了简化计算,我们假设偏差相对于零是对称的。 那么我们找到3个绝对值就足够了,每个变量一个。
deltMax-最大偏差。 设置项的值更少,更多(-deltMax,deltaMax);
divMax是偏差的最大导数。 设置项的值减少,增加(-divMax,divMax);
div2Max是最大二阶导数。 设置术语的值来减慢,加速(-div2Max,div2Max)。
umin和umax的最大和最小影响取决于设计特征,在此示例中,其取值为+30和-30。
通过优化调整调节器。
为了选择系数,我们使用与先前实验中使用的模糊逻辑相同的优化方案。
作为优化标准,我们采用不超过0.001的标准偏差,并且控制单元中的切换次数不超过25。对于切换,我们改变控制动作的符号。
控制器设置块的电路如图2所示。 9。
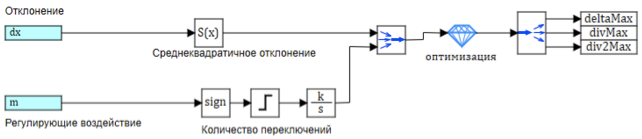
图9.配置模糊输出参数。
作为块操作的结果,获得了以下参数
deltMax = 0.00746;
divMax = 0.2657;
div2Max = 25.13;
转换结果如图10所示。
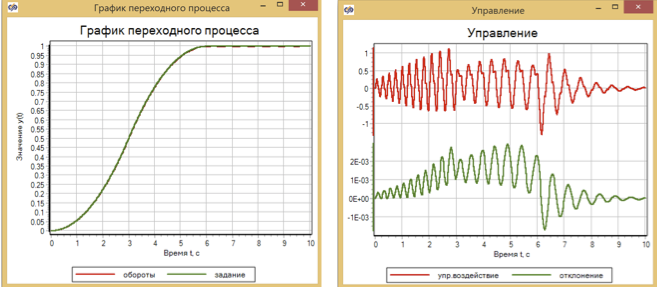
图10.使用模糊逻辑的瞬态和电机控制。
优化后的转数与机组的最大偏差为2.5×10 -3 。 从原理上讲,这还不错,但是在V.I. 设置后模型中的宾客偏差小两个数量级:最大值为5×10 -5 。
为了进行比较,我们给出了简化模型的相同模型的PID控制器操作图11和交通规则图12的结果。 还通过优化方法选择了这些调节器的参数。
结果,与基于模糊逻辑的控制器相比,PID控制器可获得更大的偏差-约为6×10 -3 ,而对于使用二阶导数的交通控制器而言,该偏差约为3×10 -3 (参见13)。 此外,在所有图表上都可以看到,当指定的影响发生变化(3秒,6秒部分的变化)时,调节的质量也会发生变化。
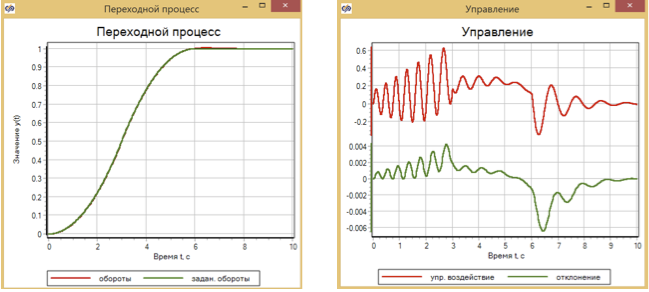
图11.使用PID控制器进行瞬态和电机控制。
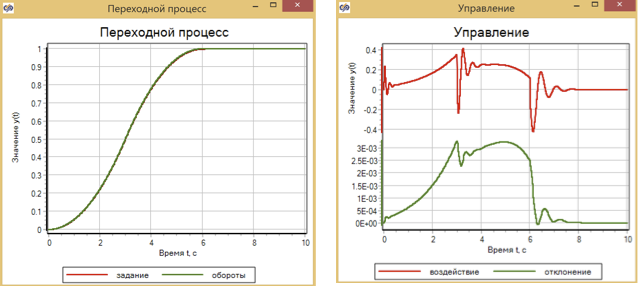
图12.在交通控制器的帮助下进行瞬态过程和引擎控制。
为了启动发动机,过渡功能以平稳的速度变化形式使用。 我们还根据该定律通过优化方法对调节器进行了调整,以实现最佳控制。 让我们尝试逐步应用效果,看看最初为平滑过渡过程而优化的调节器如何应对。
因此,在此过程的3秒内,我们使用从0到1的步进。
实验结果如图13-15所示。
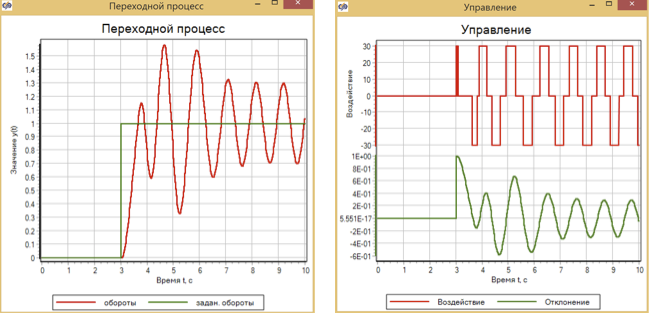
图13.具有模糊逻辑控制器的逐步控制动作的瞬态过程和控制。
可以看出,为使发动机平稳加速而调节的调节器在逐步动作期间无法应付控制,并且系统进入自动振荡模式。
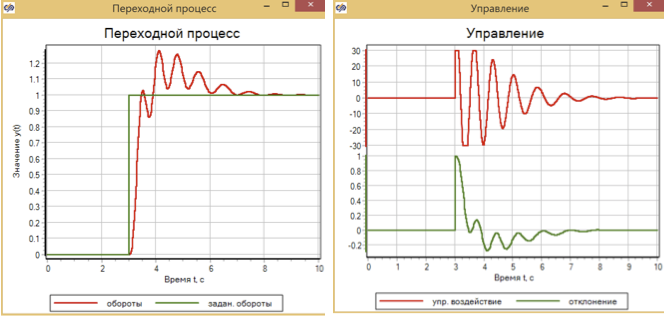
图14.带有PID控制器的带步进控制动作的瞬态过程和控制。
PID控制器已逐步调整为平滑过程,并具有逐步作用,可以过渡到预定时间,但同时有30%的过冲和4秒内的振荡过程。
交通控制器配置为平滑调节,具有逐步效果,可提供平稳过渡而不会超调(图14)
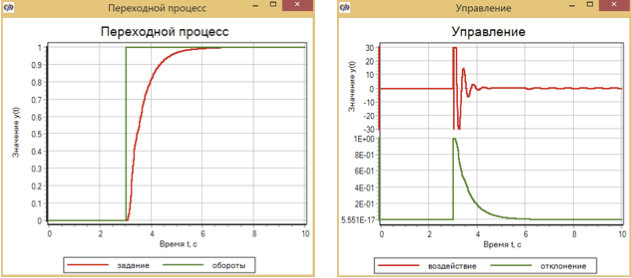
图15.过渡过程和控制,以及通过流量控制器进行的分步控制动作。
结论
这些数值实验表明,与PID和SDA相比,基于模糊逻辑的控制器可以更精确地控制简单发动机模型的转速,且设定值具有平滑的变化。
然而,事实证明,这种设置不能保证调节器在步进动作期间的稳定性。
同时,对于发动机的简化模型,在逐步动作的情况下,基于模糊逻辑的控制器要比PID或交通控制器更差。
链接到带有文章中项目的存档以进行自学