这是TensorFlow库教程。 认为它比有关手写数字识别的文章更深入。 这是有关优化方法的教程。 在这里,您不能没有数学。 如果您完全忘记它也可以。 回想一下。 没有正式的证据和复杂的结论,只有直观理解的必要最低限度。 首先,对如何在优化神经网络中使用该算法有一些背景知识。

六个月前,一个朋友问我如何用Python制作神经网络。 他的公司生产用于地球物理测量的仪器。 在钻井过程中,几种不同的探针可测量与井周围环境参数相关的一组信号。 在某些复杂的情况下,即使在功能强大的计算机上,也需要长时间根据信号精确计算环境参数,因此有必要解释现场的测量结果。 有一个想法是在一个集群上计算数十万个案例,并在它们上训练一个神经网络。 由于神经网络非常快,因此可以在钻孔过程中将其用于确定与测量信号一致的参数。 详细信息在文章中:
Kushnir,D.,Velker,N.,Bondarenko,A.,Dyatlov,G.,&Dashevsky,Y.(2018年10月29日)。 使用神经网络(俄语)对二维故障模型中的深方位电阻率工具进行实时仿真。 石油工程师协会。 doi:10.2118 / 192573-RU
一天晚上,我展示了keras如何实现简单的神经网络,并且一个工作中的朋友开始对计数的数据进行训练。 几天后,我们讨论了结果。 从我的角度来看,他看上去很有前途,但是一位朋友说他需要使用设备的精度进行计算。 如果均方误差约为1,则需要1e-3。 少3个订单。 一千次。
神经网络架构,数据规范化和优化方法的实验几乎没有结果。 几周后,一个朋友打来电话,说他安装了MatLab并通过Levenberg-Marquardt方法(以下称为LM )解决了问题。 它经过长时间(数天)的优化,无法在GPU上运行,但结果是正确的。 听起来像是一个挑战。
快速搜索用于keras或TensorFlow的现成的LM优化器失败。 我只遇到了pyrenn库,但是在我看来它的功能似乎很差。 我决定自己实施。 乍一看,一切看起来都很简单,两个晚上应该就足够了。 花了更长的时间。 有两个问题:
- TensorFlow。 一堆文章,但几乎涉及所有层次,“但让我们来写个
世界手写数字识别。” - 数学 我忘记了很多,数学文章的作者根本不在乎像我这样的人:没有解释的可靠公式,“很明显!” 等等。
结果,他为那些忘记了数学并想更深入地了解TensorFlow的人写了一篇文章,但没有硬核。 本文包含大量文本和少量代码。 当文本很少且代码很多时,相反的选择是Jupyter Notebook Levenberg-Marquardt 。
了解Rosenbrock功能
我们将通过Rosenbrock函数生成训练数据,该函数通常用作优化算法的基准:
f ( x , y ) = ( a - x ) 2 + b ( y - x 2 ) 2
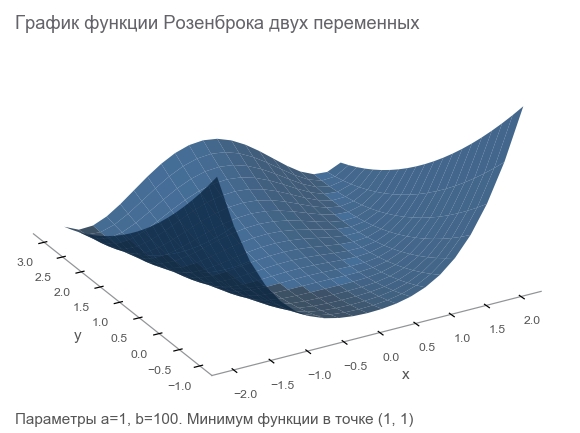
她为什么好?
- 美好的时间表。 它被称为Rosenbrock山谷和不可翻译的Rosenbrock的香蕉功能 。
- 整体最小值在一个长而狭窄的抛物线形平坦谷内。 寻找山谷是微不足道的,而全局最小值很难。
- 有一个多维选项。 要为多个变量提供出色的功能并非易事。
我们将通过连接进一步工作所需的库来开始从中编写代码:
import numpy as np import tensorflow as tf import math def rosenbrock(x, y, a, b): return (a - x)**2 + b*(y - x**2)**2
我们陈述问题
由于我们在谈论一种测量设备,因此让我们继续使用此类比喻。 我们在虚拟世界中的设备可以测量坐标 ( X , y ) 和高度 ž 。 物理学家研究了这个世界,并说:“ 是的,这是Rosenbrock!知道坐标,您就可以准确地计算高度,而无需测量。 ” 换句话说,科学家给了我们一个模型 z = R o s e n b r o c k ( x , y , a , b ) 取决于参数 ( A , b ) 。 这些参数尽管在虚构的世界中是恒定的,但未知。 需要找到它们。
我们进行了一系列实验, 米 点数 (x1,y1,z1),(x2,y2,z2),...,(xm,ym,zm) :
优化的第一种方法是尝试猜测参数。 我们使用Numpy库:
x, y = data_points[:, 0], data_points[:, 1] z = data_points[:, 2]
如何理解我们错了? 计算残差 -误差大小。 m 点给 m 残差-您需要一个积分指标。 我们将每个残差平方成一个平方并计算平均值:
MSE(a,b)= frac1m summi=1(zi− widehatzi)2
这种接近度的度量称为均方误差 (以下称为mse ):
[Out]: 3868.2291666666665
通过最小化mse ,我们解决了最小二乘问题 ( 非线性平方最小化 ):
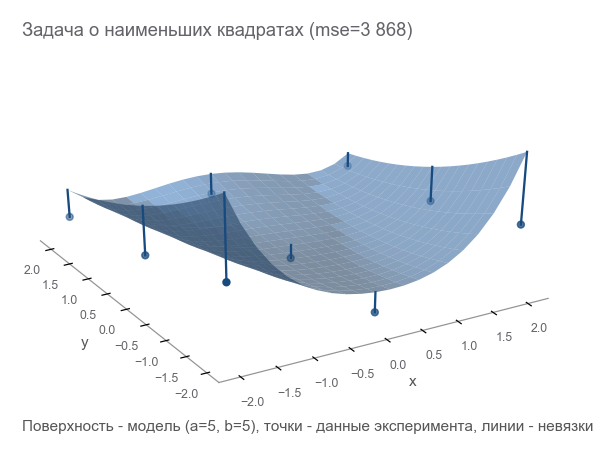
可以看出,这些参数根本没有猜测。
我们在TensorFlow上制定问题
该模型具有形式 z=Rosenbrock(x,y,a,b) 。 我们把它变成表格 y=f(x,p) (通常是数学写的 beta 代替 p 但程序员不使用beta)。 现在模型有了形式 y=Rosenbrock(x,p) 在哪里 y -身高 x 是两个元素(分量) 的坐标向量 ,并且 p -参数向量 。
程序员经常将向量视为一维数组。 这并不完全正确。 数字数组是表示向量的一种方式。 您可以将向量表示为维数组 N 二维数组 1\乘以N ,甚至是数组 N\乘以1 在向量是列向量的事实(例如,将其乘以矩阵)的情况下很重要:
\开始bmatrixx1 vdotsxN endbmatrix
TensorFlow使用张量的概念。 像数组一样, 张量可以是一维的(用于表示向量 ),二维的(用于矩阵或列向量 )和任何更大的维度。
TensorFlow代码的形式与Numpy代码相同。 内容是巨大的。 numpy代码计算出 mse 值 。 TensorFlow代码根本不执行任何计算,它形成了 mse 可以计算 的数据流 图 。 Rosenbrock功能是一个非常耐大脑的时刻。 我们在两种情况下都使用它。 但是,当我们传递Numpy数组时,它将根据公式执行计算并返回数字。 当我们将张量传输到TensorFlow时,它形成数据流的子图,并以张量的形式返回其边缘 。 多态的奇迹,但不要滥用它们:
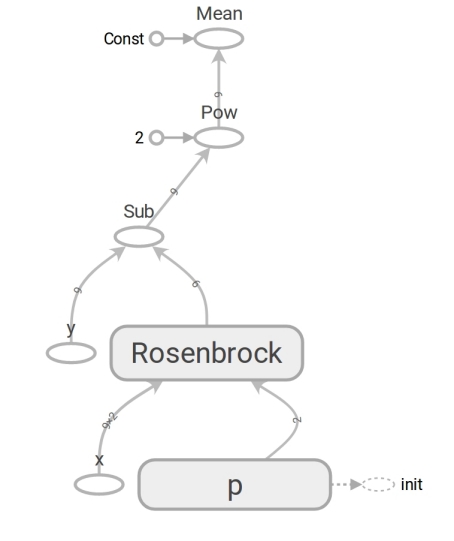
由于存在这样的数据流图,TensorFlow尤其能够自动计算导数 (使用反向模式自动微分技术)。
一点数学。 “为那些被遗忘的人”的方块将被隐藏在扰流板中。
导数(输入的数字-剩余的数字)您很可能还记得一个变量的标量(返回数字)函数的导数的定义:for f: mathbbR rightarrow mathbbR 导数 f 在这一点上 x in mathbbR 定义为:
f′(x)= limh\到0 fracf(x+h)−f(x)h
导数是衡量变化的一种方法。 在标量情况下,导数显示函数将改变多少 f 如果 x 变小 varepsilon :
f(x+ varepsilon)\大约f(x)+ varepsilonf′(x)
为了方便起见,我们表示 y=f(x) 和 y 由 x 我们将写如何 frac\部分y\部分x 。 这样的记录强调 frac\部分y\部分x -变量之间的变化率 x 和 y 。 更具体地说,如果 x 更改为 varepsilon 然后 y 更改为大约 varepsilon frac\部分y\部分x 。 您也可以这样写:
x rightarrowx+ Deltax Rightarrowy rightarrow\大约y+ frac\部分y\部分x Deltax
读为:“变化 x 在 x+ Deltax 改变 y 大约在 y+ Deltax frac\部分y\部分x “。这样的记录清楚地凸显了变更之间的联系 x 并改变 y 。
我们建立了一个数据流图,让我们运行mse计算:
[Out]: 3868.2291666666665
结果与Numpy相同。 所以他们没有弄错。
开始优化
不幸的是,无法猜测参数。 但是然后我们:
- 我们设置最佳标准-mse的最小值。
- 确定了可变参数:矢量 p 与组件 一 , b Rosenbrock函数。
- 我们还没有考虑过限制,但是还没有限制。
在最后一步中,我们构造了带有有限损失张量( 损失 函数 )的数据流图。 优化的目的是找到参数向量的值 p 损失函数的值最小。 我们很幸运,此函数的图形非常简单(凹形且没有局部最小值):
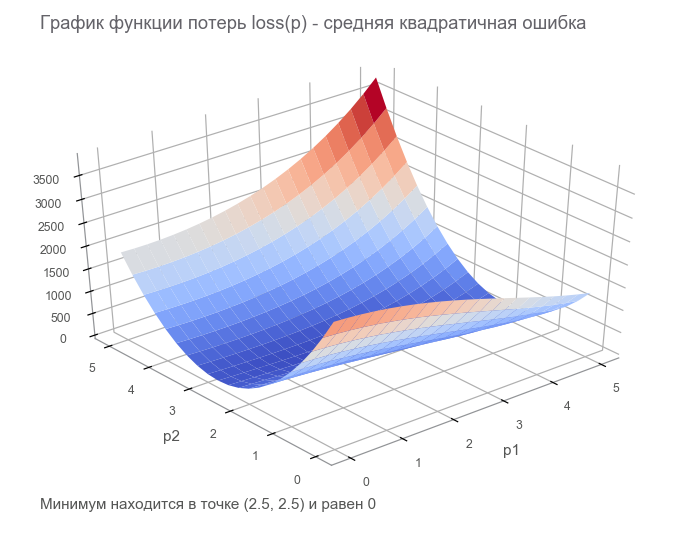
优化入门。 首先,我们编写一个广义周期:
我们通过最快的梯度下降(SGD)方法进行优化
可以将这种方法的动作与骑着大胆的滑雪者相提并论,后者总是放下斜坡(沿最陡的方向)。 在这种情况下,仅考虑该位置的坡度。 如果坡度较大,则滑雪者在下一次更改之前会飞很长一段距离。 坡度较弱时,它会缓慢移动。 也许如何飞走 进入一棵树 ( 算法发散 ),并卡在坑中( 局部最小值 )。

您可以编写如下(更改 boldsymbolp 在 boldsymbolp−... ):
boldsymbolp rightarrow boldsymbolp− alpha[ nablaploss( boldsymbolp)]
油腻的 boldsymbolp 强调这是实际位置的点-当前步骤中参数向量的值。 第一步,这是我们的猜测(5,5)。 公式中有两个有趣的地方: alpha - 学习率 ( learning rate ), nablap亏损 -通过参数向量损失函数的梯度 ( gradient )。
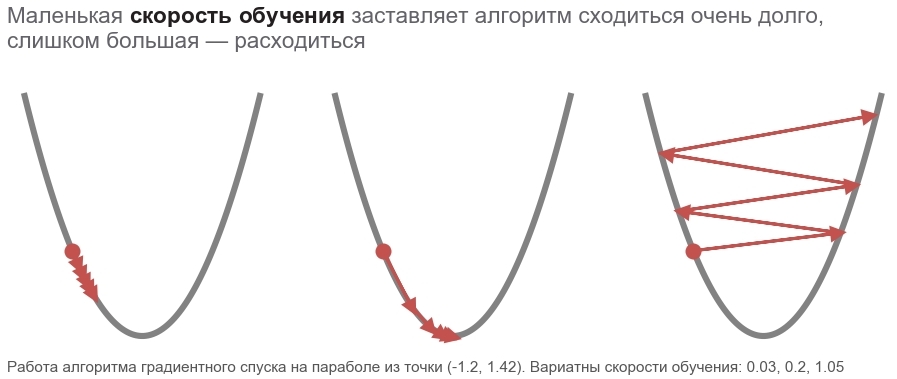
渐变(输入的矢量-左数)考虑一个将向量作为输入并产生标量的函数: f: mathbbRN rightarrow mathbbR 。 微分 f 在这一点上 x in mathbbRN 现在称为渐变 ,是一个向量 [ nablaxf(x)] in mathbbRN (称为“ nabla”)由偏导数组成:
nablaxy=( frac\部分y\部分x1, frac\部分y\部分x2,..., frac\部分y\部分xN)
在这种情况下,函数更改对参数更改的依赖关系的记录具有以下形式:
x rightarrowx+ Deltax Rightarrowy rightarrow\大约y+ nablaxy cdot Deltax
记录已发生很大变化,以考虑到 x , Deltax 和 nablaxy -中的向量 mathbbRN 和 y -标量。 向量相乘时 nablaxy 和 Deltax 使用标量乘积 (组件乘积的总和)。
[Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 1381.5379689135807 [...] ENDED ON STEP: 582, FINAL LOSS: 9.698531012270816e-11 PARAMETERS: [2.50000205 2.49999959]
采取了582个步骤:
朝反梯度方向运动为什么我们朝与梯度相反的方向移动? 调用标量乘积的条目: x rightarrowx+ Deltax Rightarrowy rightarrow\大约y+ nablaxy cdot Deltax 。 最小化 y 。 由于函数的行为仅在很小的范围内通过导数知道,因此有必要以小的但最佳的步骤移动,以使乘积最小 nablaxy cdot Deltax 。 按照学校的定义, 两个向量的标量乘积等于这些向量的长度乘以它们之间夹角的余弦的乘积 : a cdotb=\左|a\右|\左|b\右|cos\角(a,b) 。 对于固定长度的向量,此乘积的最小余弦值为-1,即 当向量指向相反方向时,它们之间的夹角为180度。 因此,最小标量积 nablaxy cdot Deltax 何时达到 Deltax 在反梯度的方向。
我们用亚当方法进行优化
我们将不进一步介绍梯度方法,但是会有很多变化。 您可以在文章优化神经网络的方法中阅读它们。 在TensorFlow中,已经实现了许多优化器。 例如,亚当:
[Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 34205.72916492336 [...] ENDED ON STEP: 317, FINAL LOSS: 2.424142714263483e-12 PARAMETERS: [2.49999969 2.50000008]
分317个步骤进行管理。 快得多。
我们用牛顿法进行优化
可以将二阶方法的作用与骑有理性的随心所欲的滑雪者进行比较,后者可以长时间考虑路线的下一个点,不仅要考虑位置的坡度,还要考虑曲率。
实际上,梯度下降法和二阶方法都试图猜测( 近似 )当前点的函数。 梯度方法仅关注函数图在一阶导数上的斜率 。 除了偏度以外,二阶方法还考虑了曲率 ,二阶导数:“如果曲率持续存在,那么最小值将在哪里?” 我们计算并去那里:
要构造这样的近似值并计算估计的最小点,可以使用泰勒级数 。 对于一维情况,在点处通过二阶多项式近似 一 看起来像这样:
f(x)\大约f(a)+ fracf′(a)(x−a)1!+ fracf″(a)(x−a)22!
最低达到 x=a− fracf′(a)f″(a) 。 多维案例看起来更严重:
黑森州矩阵(输入的矢量-左数)黑森州矩阵是由二阶导数组成的方阵:
boldsymbolHyx=\开始bmatrix frac\部分2y\部分x21& frac\部分2y\部分x1\部分x2& cdots& frac\部分2y\部分x1\部分xN frac\部分2y\部分x2\部分x1& frac\部分2y\部分x22& cdots& frac\部分2y\部分x2\部分xN vdots& vdots& ddots& vdots frac\部分2y\部分xN\部分x1和 frac\部分2y\部分xN\部分x2& cdots& frac\部分2y\部分x2N\结束bmatrix
通过梯度和Hessian矩阵对向量函数的二阶多项式的逼近 一 看起来像这样:
f(x)\大约f(a)+(xa) intercal[ nablaxf(a)]+ frac12!(xa) intercal[ boldsymbolHfx(a)](xa)
最低达到 x=a−[\粗体符号Hfx(a)]−1[ nablaxf(a)] 。 形状实际上与一维情况相符:我们将一阶导数替换为梯度,将二阶导数替换为Hessian矩阵,并进行了校正以处理向量。 将向量除以矩阵是不可能的,因此,使用乘以逆矩阵。 T表示移调 。 该公式暗示默认情况下,向量是一列。 转置将列 向量转换为行向量 。 在TensorFlow上实现时,应将其考虑在内,但方向相反:默认情况下,向量为字符串(一维张量)。 以防万一:换位不是90度的旋转,它是将行以相同顺序转换为列。
因此,牛顿法的步骤具有以下形式:
boldsymbolp rightarrow boldsymbolp−[ boldsymbolHlossp( boldsymbolp)]−1[ nablaploss( boldsymbolp)]
TensorFlow具有实现此方法的所有功能:
[Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 105.04357496954218 step: 4, current loss: 9.96663526704236 ENDED ON STEP: 6, FINAL LOSS: 5.882202372519996e-20 PARAMETERS: [2.5 2.5]
足够的6个步骤:
通过高斯-牛顿算法进行优化
牛顿法有一个缺点-黑森矩阵。 感谢TensorFlow,我们可以在一行代码中对其进行计数。 根据维基百科, 约翰·卡尔·弗里德里希·高斯 ( Johann Karl Friedrich Gauss)于1809年首次提及他的方法。 最小二乘法的几个参数的Hessian矩阵的计算将花费大量时间。 现在我们可以假设高斯-牛顿算法使用黑森 矩阵到雅可比矩阵的近似来简化计算。 但是从历史的角度来看,情况并非如此: 路德维希·奥托·黑塞 ( Ludwig Otto Hesse ,以他的名字命名的矩阵的开发者)出生于1811年-第一次提到算法后的第二年。 卡尔·古斯塔夫·雅各比 ( Carl Gustav Jacobi )5岁。
高斯-牛顿算法不适用于损失函数。 与残差功能一起使用 r(p) 。 此函数采用参数的输入向量 p 并返回残差矢量 。 在我们的例子中,向量 p 由2个组成部分(参数 一 和 b Rosenbrock函数),以及来自 m 组件(根据实验数量)。 获得vector参数的vector函数。 其派生词:
Jacobi矩阵(已输入向量-已释放向量)考虑一个以向量为输入并产生向量的函数: f: mathbbRN rightarrow mathbbRM 。 微分 f 在这一点上 x 现在有大小 N\乘以M ,称为Jacobi矩阵 ,由偏导数的所有组合组成:
boldsymbolJyx=\开始pmatrix frac\部分y1\部分x1& cdots和 frac\部分y1\部分xN vdots& ddots& vdots frac\部分yM\部分x1& cdots& frac\部分yM\部分xN\结束pmatrix
您可能会注意到Jacobi矩阵的行是分量的梯度 y 。 项 (i,j) 矩阵 frac\部分y\部分x 等于 frac\部分yi\部分xj 告诉我们会有多少变化 yi 改变时 xj 值很小。 与以前的情况一样,您可以编写:
x rightarrowx+ Deltax Rightarrowy rightarrow\大约y+ boldsymbolJyx Deltax
在这里 boldsymbolJyx 矩阵 N\乘以M 和 Deltax 大小向量 N 因此产品 boldsymbolJyx Deltax 是矩阵与向量的乘积,结果是大小为向量的向量 中号 。
为了不使字符过多而感到困惑,我们假设 boldsymbolJr -当前点的残差函数的Jacobi矩阵 boldsymbolp 。 然后可以将Gauss-Newton算法编写如下:
boldsymbolp rightarrow boldsymbolp−[ boldsymbolJ rintercal boldsymbolJr]−1 boldsymbolJ rintercalr(\粗体符号p)
形式的记录与牛顿方法的记录完全一致。 仅代替黑森州矩阵 boldsymbolJ rintercal boldsymbolJr 而不是渐变 boldsymbolJ rintercalr( boldsymbolp) 。 接下来,我们将了解为什么可以使用这种近似。 同时,让我们继续在TensorFlow上实施:
[Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 14.653025157673625 step: 4, current loss: 4.3918079172783016e-07 ENDED ON STEP: 4, FINAL LOSS: 3.374364957618591e-17 PARAMETERS: [2.5 2.5]
足够4个步骤。 少于牛顿的方法。
从代码可以看出,损失函数未用于优化,仅用于停止和记录标准。 优化算法如何知道最小化哪个函数? 答案令人惊讶:没办法! 高斯-牛顿只使均方误差最小。
修正文章的数学部分
我们重复了所有需要的数学运算。 让我们对其进行一些修复,以进一步仅专注于编程和TensorFlow。 您可能需要一支铅笔来追踪数学动作的顺序。
有模特儿 y=f(x,p) 在哪里 x -矢量 p -尺寸参数向量 n 和 y -标量。 从收到的实验 m 点数 (x1,y1),...,(xm,ym) ( 数据对 )。 向量残差函数仅取决于参数向量: r(p)=(r1(p),...rm(p)) 在哪里 rk(p)=yk− widehatyk=yk−f(xk,p) 。 , p , xk,yk ? , xk,yk , .
p , ( sum of squared error — sse residual sum-of-squares — rss ) . mse sse , m 。 . :
loss(p)=r21(p)+⋯+r2m(p)=m∑k=1r2k(p)
p (p) 。
, . — . — , r2 2r∂r∂p 。 :
∇ploss=(m∑k=12rk∂rk∂p1,⋯,m∑k=12rk∂rk∂pn)
. :
[ ħ 升ö 小号小号p ] 我Ĵ = ∂ 2升ö 小号小号∂ p 我 ∂ p Ĵ =米Σ ķ=1(2∂ř ķ∂ p 我 ∂ř ķ∂ p Ĵ +2- [Rķ∂2- [R ķ∂ p 我 ∂ p Ĵ)
. , , (uv)′=u′v+uv′ 。
太好了! .
, , , — 2rk∂2rk∂pi∂pj 。 , , rk , . — . , ? -.
:
Jr=(∂r1∂p1⋯∂r1∂pn⋮⋱⋮∂rm∂p1⋯∂pm∂pn)
, , . 注意:
2J⊺rJr≈Hlossp
"" . ( ). , — 2rk∂2rk∂pi∂pj , .
( ):
2J⊺rr=∇ploss
, , - — , mse .
. , , . m (x1,y1),...,(xm,ym) , y=rosenbrock(x,p) 。 p , .
, : " . - ! ". , , , ( supervised learning ). , . : ( training set ) — ; — ( prediction model ) ; — , .
( multi-layer perceptron neural network mlp ). , , :
- ( starting values ) . Xavier'a, .
- ( overfitting ). — . , . — .
- ( scaling of the input ). , .
9 . 500:
500 . — ( learner ), ( outcome measurement ) ( features ) .
( network diagram ). MatLab:
( input ). W ( weights ) 2x10, b ( bias ) 10, ( activation ). () ( hidden layer ) 10 . , , ( output ).
, , ( tanh ):
h1=tanh(xW1+b1)ˆy=h1W2+b2
:
h1=tanh([x1x2][w(1)1,1⋯w(1)1,10w(1)2,1⋯w(1)2,10]+[b(1)1⋯b(1)10])ˆy=[h(1)1⋯h(1)10][w(2)1,1⋮w(2)1,10]+b2
. W1 "" h1 , - W2 。 41 . , .
m×2 , . - ˆy 来自 m :
Adam
Adam rosenbrock 。 mse :
[Out]: step: 1, current loss: 671.4242576535694 [...] ENDED ON STEP: 40000, FINAL LOSS: 0.22862158574440725 VALIDATION LOSS: 0.29000289644978866
. : , , .
rosenbrock 2 . :
:
Jrp . , 4 W1,b1,W2,b2 。 4 JrW1,Jrb1,JrW2,Jrb2 tf.concat .
. tf.while_loop , ri , , stack .
ri W1 : [∂ri∂w(1)1,1⋯∂ri∂w(1)1,10∂ri∂w(1)2,1⋯∂ri∂w(1)2,10] 。 tf.reshape (-1,) [∂ri∂w(1)1,1⋯∂ri∂w(1)1,10∂ri∂w(1)2,1⋯∂ri∂w(1)2,10] 。
. - . — TensorFlow . — - - W1,b1,W2,b2 。 -. Levenberg-Marquardt Jupyter Notebook rosenbrock_train.py . , TensorFlow . - , ( ) , , .
-
hess_approx grad_approx -. rosenbrock , . :
- : Δp=[Δw(1)1,1⋯Δw(1)2,10Δb(1)1⋯Δb(1)10Δw(2)1,1⋯Δw(2)1,10Δb2]
- :
ΔW1=[Δw(1)1,1⋯Δw(1)2,10] , Δb1=[Δb(1)1⋯Δb(1)10] , ΔW2=[Δw(2)1,1⋯Δw(2)1,10] , Δb2=[Δb2] 。 - , :
ΔW1=[Δw(1)1,1⋯Δw(1)1,10Δw(1)2,1⋯Δw(1)2,10] , ΔW2=[Δw(2)1,1⋮Δw(2)1,10] - .
[Out]: step: 1, current loss: 548.8468777701685 step: 2, current loss: 49648941.340197295 InvalidArgumentError: Input is not invertible.
出了点问题。 , . - , .
, .
-
. Matlab trainlm . . MathWorks.
- : p→p−[J⊺rJr]−1J⊺rr(p) 。 - :
p→p−[J⊺rJr+μI]−1J⊺rr(p)
\亩 我 n ( ). \亩 , -. , . , LM -.
:
mu = tf.placeholder(tf.float64, shape=[1]) n = tf.add_n(parms_sizes) I = tf.eye(n, dtype=tf.float64)
\亩 ? LM - . , . , \亩 , . — , mse . , :
[Out]: step: 1, mu: 3.0 current loss: 692.6211687622557 [...] ENDED ON STEP: 100, FINAL LOSS: 0.012346989371823602 VALIDATION LOSS: 0.01859463694102034
100 LM mse 10 , 40 .
. , . , rosenbrock_train.py .
2D . . . , " " ( curse of dimentionality , Bellman, 1961). . .
:
f(x)=N−1∑i=1[100(xi+1−x2i)2+(1−xi)2],x=[x1⋯xN]∈RN
rosenbrock_train.py get_rand_rosenbrock_points .
-
- : " ! 4 , 300! ". , ( ) -. , , . - . . : ? , . . , - :
- 10 000 6D .
- 3 12, 10, 8 (311 ).
- .
- 3.5 .
. - 2 . LM . 20 .
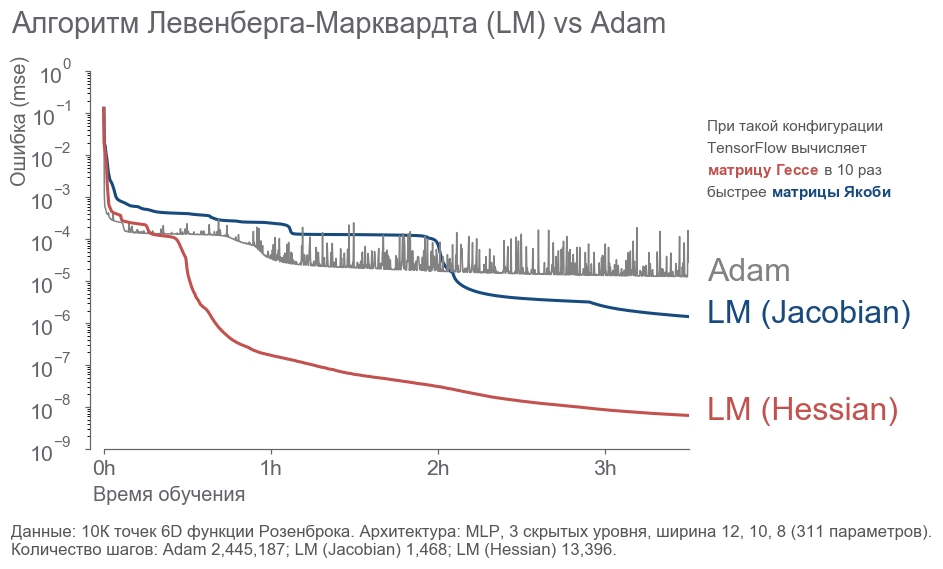
rosenbrock_train.py . . , .
结论
, . " ", , . , . , 273 . - , .
, :
- .
- ( ) -:
[1] Petros Drineas, Ravi Kannan, and Michael W. Mahoney. 2006. Fast Monte Carlo Algorithms for Matrices I: Approximating Matrix Multiplication. SIAM J. Comput. 36, 1 (July 2006), 132-157. DOI= http://dx.doi.org/10.1137/S0097539704442684
[2] Adelman, M., & Silberstein, M. (2018). Faster Neural Network Training with Approximate Tensor Operations. CoRR, abs/1805.08079.
, - . , . "".