如何在SHAP中解释模型预测

数据科学领域中最重要的任务之一不仅是构建能够做出高质量预测的模型，而且还要具有解释此类预测的能力。

如果我们不仅知道客户倾向于购买产品，而且了解什么会影响其购买，那么我们将来将能够制定公司战略以提高销售效率。

或者该模型预测患者会很快生病。 这种预测的准确性不是很高，因为 该模型隐藏了许多因素，但是对模型做出这种预测的原因的解释可以帮助医生注意新的症状。 因此，如果模型本身的精度不太高，则有可能扩大模型的应用范围。

在这篇文章中，我想谈谈SHAP技术，它使您可以查看各种模型的内幕 。

如果线性模型变得越来越不清晰，则预测器下系数的绝对值越大，则该预测器越重要，那么说明相同梯度增强的特征的重要性就变得更加困难。

为什么需要这样的图书馆

在sklearn堆栈的xgboost lightGBM软件包中，内置了用于评估“木制模型”的特征重要性（特征重要性）的方法：

1. 增益
   此度量显示每个特征对模型的相对贡献。 为了进行计算，我们遍历每棵树，查看每个树节点，该特征导致节点的划分，并且模型不确定性根据度量（基尼杂质，信息增益）降低了多少。
   对于每个功能，总结了其对所有树木的贡献。
   
2. 封面
   显示每个功能的观测数量。 例如，您有4个要素，3棵树。 假设树的节点上的特征1在树1、2和3中分别包含10、5和2个观测值，那么对于该特征，重要性为17（10 + 5 + 2）。
   
3. 频次
   显示此功能在树的节点中出现的频率，即，考虑了每棵树中每个功能被分成节点的树的总数。
   

所有这些方法的主要问题在于，尚不清楚此功能究竟如何影响模型预测。 例如，我们了解到收入水平对于评估银行客户偿还贷款的偿付能力很重要。 但是到底如何呢？ 较高的收入偏向模型预测？

当然，我们可以通过改变收入水平做出一些预测。 但是如何处理其他功能？ 毕竟，我们发现自己处于一种状况，需要独立于其他特征及其平均值来了解收入的影响。

有一种普通的银行客户“处于真空状态”。 模型预测将如何随着收入的变化而变化？

在这里， SHAP库可以解救。

我们使用SHAP计算功能的重要性

在SHAP库中，为了评估要素的重要性， 计算了Shapley值 （通过美国数学家的名字命名，并命名了该库）。

为了评估功能的重要性，在有或没有此功能的情况下评估模型预测。

一些史前史

Shapley的含义来自博弈论。

考虑这种情况：一群人打牌。 如何根据他们的贡献在他们之间分配奖金？

有许多假设：

• 每个玩家的奖励金额等于总奖池
• 如果两个玩家对游戏做出相等贡献，他们将获得相等的奖励。
• 如果玩家未做出任何贡献，则不会获得奖励。
• 如果玩家花了两场比赛，那么他的总奖赏包括每场比赛的奖赏金额

我们以参与者的身份介绍模型的特征，并以奖池形式作为模型的最终预测。

让我们来看一个例子。

第i个特征的Shapley值的计算公式：

$$$$ display $$ \ begin {equation *} \ phi_ {i}（p）= \ sum_ {S \ subseteq N / \ {i \}} \ frac {| S |！（n-| S | -1） ！} {n！}（p（S \ cup \ {i \}）-p（S））\ end {equation *} $$显示$$

在这里：

$$$p（S \ cup \ {i \}）$ 是对具有第i个特征的模型的预测，
$$$p（S）$-这是没有第i个功能的模型的预测，
$$$n$-功能数量，
$$$S$-没有第i个特征的任意一组特征

第i个特征的Shapley值是针对每个数据样本（例如，样本中的每个客户）在所有可能的特征组合（包括不存在所有特征）上计算的，然后对求得的值取模值求和，并获得第i个特征的最终重要性。

这些计算非常昂贵，因此，在幕后，使用了各种算法来优化计算，有关更多详细信息，请参见上面github上的链接。

以xgboost文档中的vanilla为例。



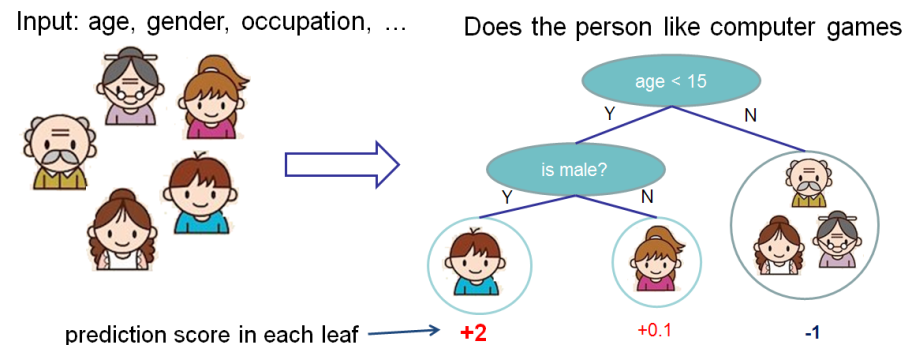
我们想评估功能对预测人是否喜欢计算机游戏的重要性。

在此示例中，为简单起见，我们具有两个功能：年龄（年龄）和性别（性别）。 性别（性别）取值为0和1。

以Bobby（树的最左节点中的小男孩）为基础，计算特征年龄（年龄）的Shapley值。

我们有两组S功能：

$$$\ {\}$ -没有功能
$$$\ {性别\}$ -只有一个特征性别。

没有要素值的情况

在没有数据样本功能的情况下，即对于所有功能而言，值均为NULL的情况下，不同模型的工作方式有所不同。

在这种情况下，将考虑模型对树枝的预测取平均值，即没有特征的预测为 $$$[（2 + 0.1）/ 2 +（-1）] / 2 = 0.025$。

如果我们增加年龄知识，那么模型的预测将是 $$$（2 + 0.1）/ 2 = 1.05$。

结果，对于缺少要素的情况，Shapley的值是：

$$

$$\ frac {| S |！（n-| S | -1）！} {n！}（p（S \ cup \ {i \}）-p（S））= \ frac {1（2-0 -1）！} {2！}（1.025）= 0.5125$$

知道性别的状况

对于鲍比 $$${性别}$没有特征年龄的预测，只有具有特征的性别相等 $$$[（2 + 0.1）/ 2 +（-1）] / 2 = 0.025$。 如果我们知道年龄，则预测是最左边的树，即2。

结果，在这种情况下，Shapley的值是：

$$$$显示$$ \开始{equation *} \ frac {| S |！（n-| S | -1）！} {n！}（p（S \ cup \ {i \}）-p（S） ）= \ frac {1（2-1-1）！} {2！}（1.975）= 0.9875 \ end {equation *} $$显示$$

总结一下

Shapley对于特征年龄（年龄）的总值：

$$$$ display $$ \开始{equation *} \ phi_ {Age Bobby} = 0.9875 + 0.5125 = 1.5 \ end {equation *} $$ display $$

一个真实的商业例子

SHAP库具有丰富的可视化功能，可帮助轻松，简单地为业务和分析师自己解释模型，以评估模型的充分性。

在其中一个项目中，我分析了公司员工的外流情况。 作为模型，使用了xgboost。

python中的代码：

import shap shap_test = shap.TreeExplainer(best_model).shap_values(df) shap.summary_plot(shap_test, df, max_display=25, auto_size_plot=True) 

结果显示的功能重要性：



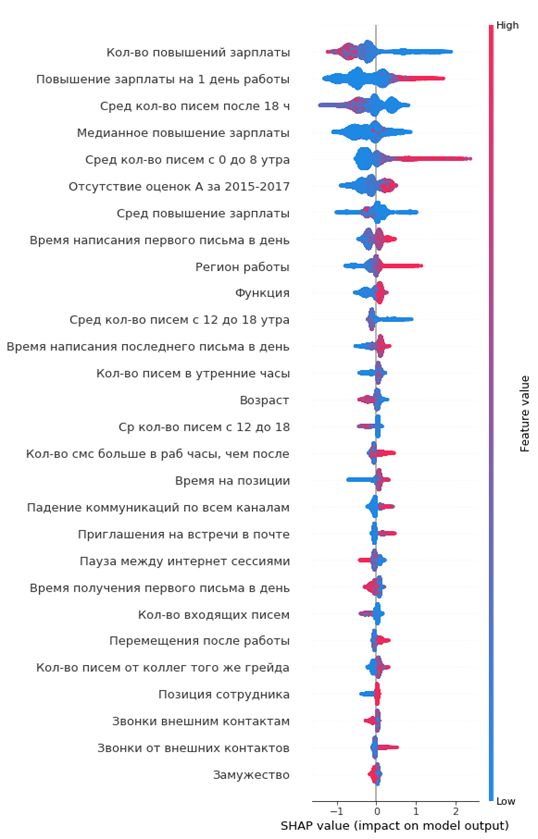
如何阅读：

• 中心垂直线左侧的值是负数（0），右侧是-正数（1）
• 图上的线越粗，观察点越多
• 图表上的点越红，则其中的要素值越高

从图表中，您可以得出有趣的结论并检查其适当性：

• 员工的薪水增长越低，离职的可能性就越大
• 有些办公室的资金流出较高
• 员工越年轻，离职的可能性越高
• ...

您可以立即构成即将离任的员工的肖像：她没有提高薪水，他还很年轻，单身，长期担任一个职位，没有升职，没有很高的年度评级，他开始很少与同事交流。

简单方便！

您可以解释特定员工的预测：



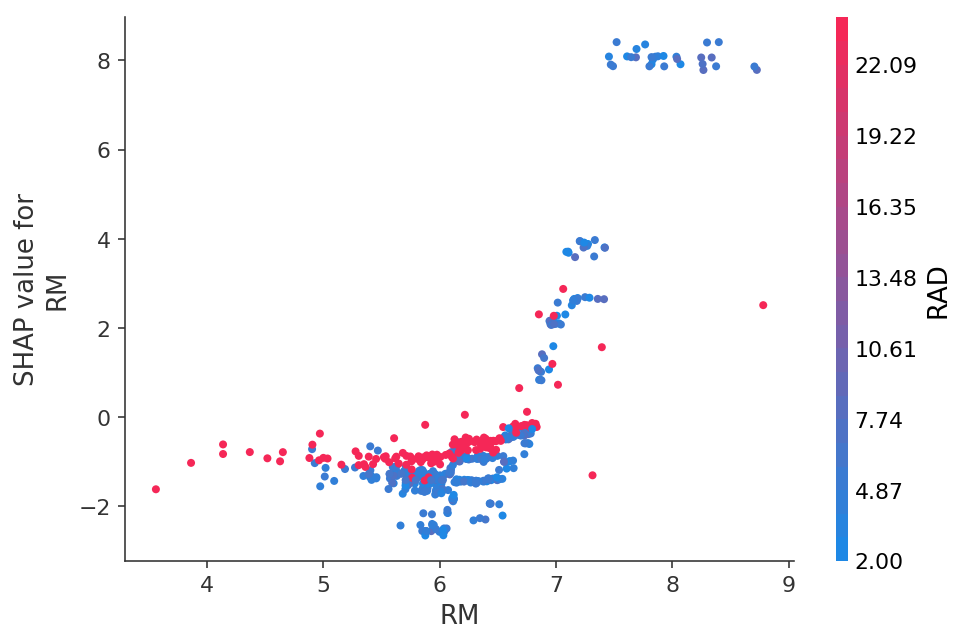
或者以2D图形的形式查看预测对特定特征的依赖关系：



您甚至可以在图片中可视化神经网络的预测：

结论

我自己大约在六个月前了解了SHAP值，这完全替代了其他评估功能重要性的方法。

主要优点：

• 方便的可视化和解释
• 诚实地计算功能的重要性
• 评估特定数据子样本的功能（例如，我们的客户与样本中其他客户有何不同）的功能是通过对熊猫中的数据集进行简单过滤并进行整形分析（实际上是几行代码）来完成的