我们使用神经网络对函数进行近似

为了开发用于神经网络的库，我们将使用神经网络算法进行训练和预测，解决逼近单个参数功能的问题。

参赛作品

设函数f为：[x0，x1]-> R

我们通过公式近似给定的函数f

P(x) = SUM W[i]*E(x,M[i]) 

在哪里

• i = 1..n
• R的M [i]
• R的W [i]
• 对于x <M; E（x，M）= {0; 1/2，x = M； 1，对于x> M

显然，在间隔（x0，x1）上M [i]的值均匀分布的情况下，存在这样的量W [i]，对于这些量而言，公式P（x）最能近似函数f（x）。 此外，对于在间隔（x0，x1）上定义并按升序排列的M [i]的给定值，我们可以描述一种用于计算公式P（x）的量W [i]的顺序算法。

这是神经网络

我们将公式P（x）= SUM W [i] * E（x，M [i]）转换为具有一个输入神经元，一个输出神经元和n个隐藏层神经元的神经网络模型。

 P(x) = SUM W[i]*S(K[i]*x + B[i]) + C 

在哪里

• 变量x-由一个神经元组成的“输入”层
• {K，B}-“隐藏”层的参数，由n个神经元和激活函数组成-S形
• {W，C}-“输出”层的参数，由一个神经元组成，用于计算其输入的加权总和。
• S是S型

一会儿

• “隐藏”层的初始参数K [i] = 1
• “隐藏”层B [i]的初始参数均匀分布在段（-x1，-x0）上

通过在函数f的值的样本（x，y）上训练神经网络，可以确定神经网络K，B，W和C的所有参数。

乙状结肠

乙状结肠是光滑的单调递增非线性函数

• S（x）= 1 /（1 + exp（-x））。

程序

我们使用Tensorflow软件包来描述我们的神经网络。

 #        x = tf.placeholder(tf.float32, [None, 1], name="x") #        y = tf.placeholder(tf.float32, [None, 1], name="y") #   nn = tf.layers.dense(x, hiddenSize, activation=tf.nn.sigmoid, kernel_initializer=tf.initializers.ones(), bias_initializer=tf.initializers.random_uniform(minval=-x1, maxval=-x0), name="hidden") #   model = tf.layers.dense(nn, 1, activation=None, name="output") #    cost = tf.losses.mean_squared_error(y, model) train = tf.train.GradientDescentOptimizer(learn_rate).minimize(cost) 

培训课程

 init = tf.initializers.global_variables() with tf.Session() as session: session.run(init) for _ in range(iterations): train_dataset, train_values = generate_test_values() session.run(train, feed_dict={ x: train_dataset, y: train_values }) 

全文

 import math import numpy as np import tensorflow as tf import matplotlib.pyplot as plt x0, x1 = 10, 20 #    test_data_size = 2000 #      iterations = 20000 #    learn_rate = 0.01 #   hiddenSize = 10 #    #     def generate_test_values(): train_x = [] train_y = [] for _ in range(test_data_size): x = x0+(x1-x0)*np.random.rand() y = math.sin(x) #   train_x.append([x]) train_y.append([y]) return np.array(train_x), np.array(train_y) #        x = tf.placeholder(tf.float32, [None, 1], name="x") #        y = tf.placeholder(tf.float32, [None, 1], name="y") #   nn = tf.layers.dense(x, hiddenSize, activation=tf.nn.sigmoid, kernel_initializer=tf.initializers.ones(), bias_initializer=tf.initializers.random_uniform(minval=-x1, maxval=-x0), name="hidden") #   model = tf.layers.dense(nn, 1, activation=None, name="output") #    cost = tf.losses.mean_squared_error(y, model) train = tf.train.GradientDescentOptimizer(learn_rate).minimize(cost) init = tf.initializers.global_variables() with tf.Session() as session: session.run(init) for _ in range(iterations): train_dataset, train_values = generate_test_values() session.run(train, feed_dict={ x: train_dataset, y: train_values }) if(_ % 1000 == 999): print("cost = {}".format(session.run(cost, feed_dict={ x: train_dataset, y: train_values }))) train_dataset, train_values = generate_test_values() train_values1 = session.run(model, feed_dict={ x: train_dataset, }) plt.plot(train_dataset, train_values, "bo", train_dataset, train_values1, "ro") plt.show() with tf.variable_scope("hidden", reuse=True): w = tf.get_variable("kernel") b = tf.get_variable("bias") print("hidden:") print("kernel=", w.eval()) print("bias = ", b.eval()) with tf.variable_scope("output", reuse=True): w = tf.get_variable("kernel") b = tf.get_variable("bias") print("output:") print("kernel=", w.eval()) print("bias = ", b.eval()) 

就是这样

• 蓝色是原始功能。
• 红色-函数的近似值

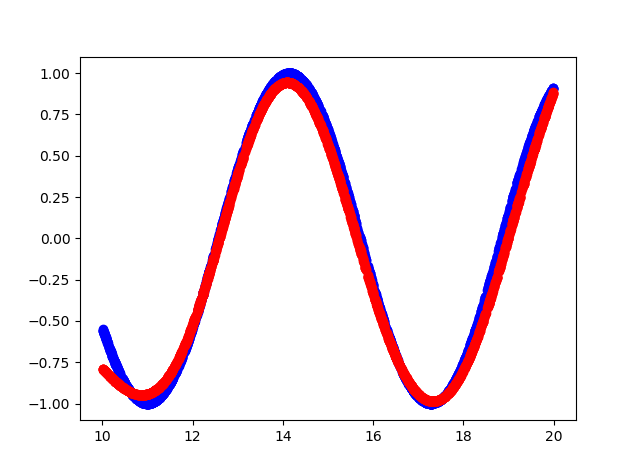
控制台输出

 cost = 0.15786637365818024 cost = 0.10963975638151169 cost = 0.08536215126514435 cost = 0.06145831197500229 cost = 0.04406769573688507 cost = 0.03488277271389961 cost = 0.026663536205887794 cost = 0.021445846185088158 cost = 0.016708852723240852 cost = 0.012960446067154408 cost = 0.010525770485401154 cost = 0.008495906367897987 cost = 0.0067353141494095325 cost = 0.0057082874700427055 cost = 0.004624188877642155 cost = 0.004093789495527744 cost = 0.0038146725855767727 cost = 0.018593043088912964 cost = 0.010414039716124535 cost = 0.004842184949666262 hidden: kernel= [[1.1523403 1.181032 1.1671464 0.9644377 0.8377886 1.0919508 0.87283015 1.0875995 0.9677301 0.6194152 ]] bias = [-14.812331 -12.219926 -12.067375 -14.872566 -10.633507 -14.014006 -13.379829 -20.508204 -14.923473 -19.354435] output: kernel= [[ 2.0069902 ] [-1.0321712 ] [-0.8878887 ] [-2.0531905 ] [ 1.4293027 ] [ 2.1250408 ] [-1.578137 ] [ 4.141281 ] [-2.1264815 ] [-0.60681605]] bias = [-0.2812019] 

源代码

https://github.com/dprotopopov/nnfunc