我向您介绍《 Anaconda的动手数据科学》一书的一章翻译
“预测性数据分析-建模和验证”
我们进行各种数据分析的主要目标是寻找模式,以预测未来可能发生的情况。 对于股票市场,研究人员和专家进行了各种测试以了解市场机制。 在这种情况下,您可以提出很多问题。 未来五年市场指数将如何变化? IBM的下一个价格范围是多少? 未来市场波动会增加还是减少? 如果政府改变税收政策会产生什么影响? 如果一个国家与另一国发动贸易战,可能会有什么得失? 我们如何通过分析一些相关变量来预测消费者的行为? 我们可以预测研究生成功毕业的可能性吗? 我们能否在一种特定疾病的特定行为之间找到联系?
因此,我们将考虑以下主题:
- 了解预测数据分析
- 有用的数据集
- 预测未来事件
- 选型
- 格兰杰因果检验
了解预测数据分析
人们可能对未来事件有很多疑问。
- 投资者如果能够预测股价的未来走势,就可以赚取巨额利润。
- 公司如果能够预测其产品趋势,则可以提高其股价和市场份额。
- 各国政府如果可以预测人口老龄化对社会和经济的影响,则将更有动力根据国家预算和其他相关战略决策制定更好的政策。
- 大学,如果他们能很好地了解毕业生的素质和技能,就可以制定一套更好的计划或启动新计划来满足未来的劳动力需求。
为了获得更好的预后,研究人员应考虑许多问题。 例如,样本数据是否太小? 如何删除缺失的变量? 该数据集在数据收集程序方面是否有偏见? 我们如何看待极端或排放? 什么是季节性,我们该如何应对? 我们应该使用什么型号? 本章将解决其中一些问题。 让我们从一个有用的数据集开始。
有用的数据集
最好的数据来源之一是
UCI机器学习存储库 。 访问该站点后,我们将看到以下列表:

例如,如果选择第一个数据集(鲍鱼),我们将看到以下内容。 为了节省空间,仅显示顶部:

用户可以从此处下载数据集并查找变量定义。 以下代码可用于加载数据集:
dataSet<-"UCIdatasets" path<-"http://canisius.edu/~yany/RData/" con<-paste(path,dataSet,".RData",sep='') load(url(con)) dim(.UCIdatasets) head(.UCIdatasets)
相应的输出如下所示:

根据先前的结论,我们知道在数据集中有427个观测值(数据集)。 对于它们每个,我们都有7个相关的函数,例如
Name,Data_Types,Default_Task,Attribute_Types,N_Instances (实例数),
N_Attributes (属性数)和
Year 。 可以将名为
Default_Task的变量解释为每个数据集的主要用途。 例如,可以将名为
Abalone的第一个数据集用于
分类 。
unique()函数可用于搜索此处显示的所有可能的
Default_Task :
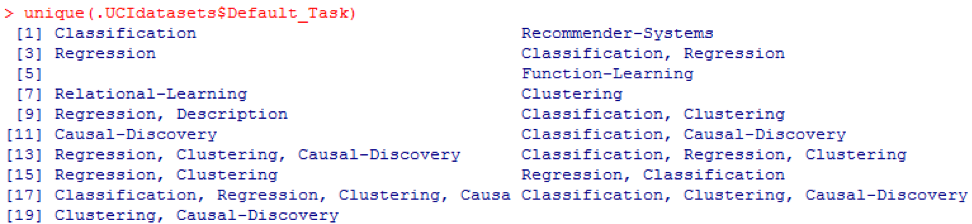
R包AppliedPredictiveModeling
该软件包包括许多可用于本章和其他章节的有用数据集。 查找这些数据集的最简单方法是使用如下所示的
help()函数:
library(AppliedPredictiveModeling) help(package=AppliedPredictiveModeling)
在这里,我们显示了一些加载这些数据集的示例。 要加载一个数据集,我们使用
data()函数。 对于第一个称为
balone的数据集,我们具有以下代码:
library(AppliedPredictiveModeling) data(abalone) dim(abalone) head(abalone)
输出如下:

有时,大型数据集包括几个子数据集:
library(AppliedPredictiveModeling) data(solubility) ls(pattern="sol")
[1] "solTestX" "solTestXtrans" "solTestY" [4] "solTrainX" "solTrainXtrans" "solTrainY"
要加载每个数据集,我们可以使用函数
dim() ,
head() ,
tail()和
summary() 。
时间序列分析
时间序列可以定义为在连续的时间点获得的一组值,它们之间通常间隔相等。 有不同的时间段,例如每年,每季度,每月,每周和每天。 对于GDP(国内生产总值)的时间序列,我们通常使用季度或年度。 对于报价-每年,每月和每天的频率。 使用以下代码,我们可以获取季度和年度的美国GDP数据:
ath<-"http://canisius.edu/~yany/RData/" dataSet<-"usGDPannual" con<-paste(path,dataSet,".RData",sep='') load(url(con)) head(.usGDPannual)
YEAR GDP 1 1930 92.2 2 1931 77.4 3 1932 59.5 4 1933 57.2 5 1934 66.8 6 1935 74.3
dataSet<-"usGDPquarterly" con<-paste(path,dataSet,".RData",sep='') load(url(con)) head(.usGDPquarterly)
DATE GDP_CURRENT GDP2009DOLLAR 1 1947Q1 243.1 1934.5 2 1947Q2 246.3 1932.3 3 1947Q3 250.1 1930.3 4 1947Q4 260.3 1960.7 5 1948Q1 266.2 1989.5 6 1948Q2 272.9 2021.9
但是,对于时间序列分析,我们有很多问题。 例如,从宏观经济学的角度来看,我们有商业或经济周期。 行业或公司可能具有季节性。 例如,利用农业,农民将在春季和秋季花费更多,而在冬季花费更少。 对于零售商而言,他们将在今年年底大量涌入资金。
要操纵时间序列,我们可以使用R包中包含的许多有用功能,称为
timeSeries 。 在示例中,我们采用每周一次的每日平均数据:
library(timeSeries) data(MSFT) x <- MSFT by <- timeSequence(from = start(x), to = end(x), by = "week") y<-aggregate(x,by,mean)
我们还可以使用
head()函数查看一些观察结果:
head(x)
GMT Open High Low Close Volume 2000-09-27 63.4375 63.5625 59.8125 60.6250 53077800 2000-09-28 60.8125 61.8750 60.6250 61.3125 26180200 2000-09-29 61.0000 61.3125 58.6250 60.3125 37026800 2000-10-02 60.5000 60.8125 58.2500 59.1250 29281200 2000-10-03 59.5625 59.8125 56.5000 56.5625 42687000 2000-10-04 56.3750 56.5625 54.5000 55.4375 68226700
head(y)
GMT Open High Low Close Volume 2000-09-27 63.4375 63.5625 59.8125 60.6250 53077800 2000-10-04 59.6500 60.0750 57.7000 58.5500 40680380 2000-10-11 54.9750 56.4500 54.1625 55.0875 36448900 2000-10-18 53.0375 54.2500 50.8375 52.1375 50631280 2000-10-25 61.7875 64.1875 60.0875 62.3875 86457340 2000-11-01 66.1375 68.7875 65.8500 67.9375 53496000
预测未来事件
尝试预测未来时,可以使用许多方法,例如移动平均,回归,自回归等。首先,让我们从最简单的移动平均开始:
movingAverageFunction<- function(data,n=10){ out= data for(i in n:length(data)){ out[i] = mean(data[(i-n+1):i]) } return(out) }
在前面的代码中,周期数的默认值为10。我们可以使用包含在名为
timeSeries的R包中的MSFT数据集(请参见以下代码):
library(timeSeries) data(MSFT) p<-MSFT$Close
[1] 60.6250 61.3125 60.3125 59.1250 56.5625 55.4375
head(ma)
[1] 60.62500 61.31250 60.75000 60.25000 58.66667 57.04167
mean(p[1:3])
[1] 60.75
mean(p[2:4])
[1] 60.25
在手动模式下,我们发现
x的前三个值的平均值与
y的第三个值匹配。 在某种程度上,我们可以使用移动平均线来预测未来。
在以下示例中,我们将展示如何评估明年的预期市场回报。 在这里,我们使用S&P500指数和历史平均年值作为我们的预期值。 前几个命令用于加载名为
.sp500monthly的相关数据集。 该计划的目的是评估平均年平均值和90%的置信区间:
library(data.table) path<-'http://canisius.edu/~yany/RData/' dataSet<-'sp500monthly.RData' link<-paste(path,dataSet,sep='') load(url(link))
[min mean max ]
cat(min2,ourMean,max2,"\n")
0.05032956 0.09022369 0.1301178
从结果中可以看出,S&P500的历史平均年回报率为9%。 但是我们不能说明年该指数的盈利能力将是9%,因为 可能在5%到13%之间,而且波动很大。
季节性
在下面的示例中,我们展示了自相关的用法。 首先,我们下载一个名为
astsa的R包,它表示应用统计时间序列分析。 然后,我们以季度频率加载美国GDP:
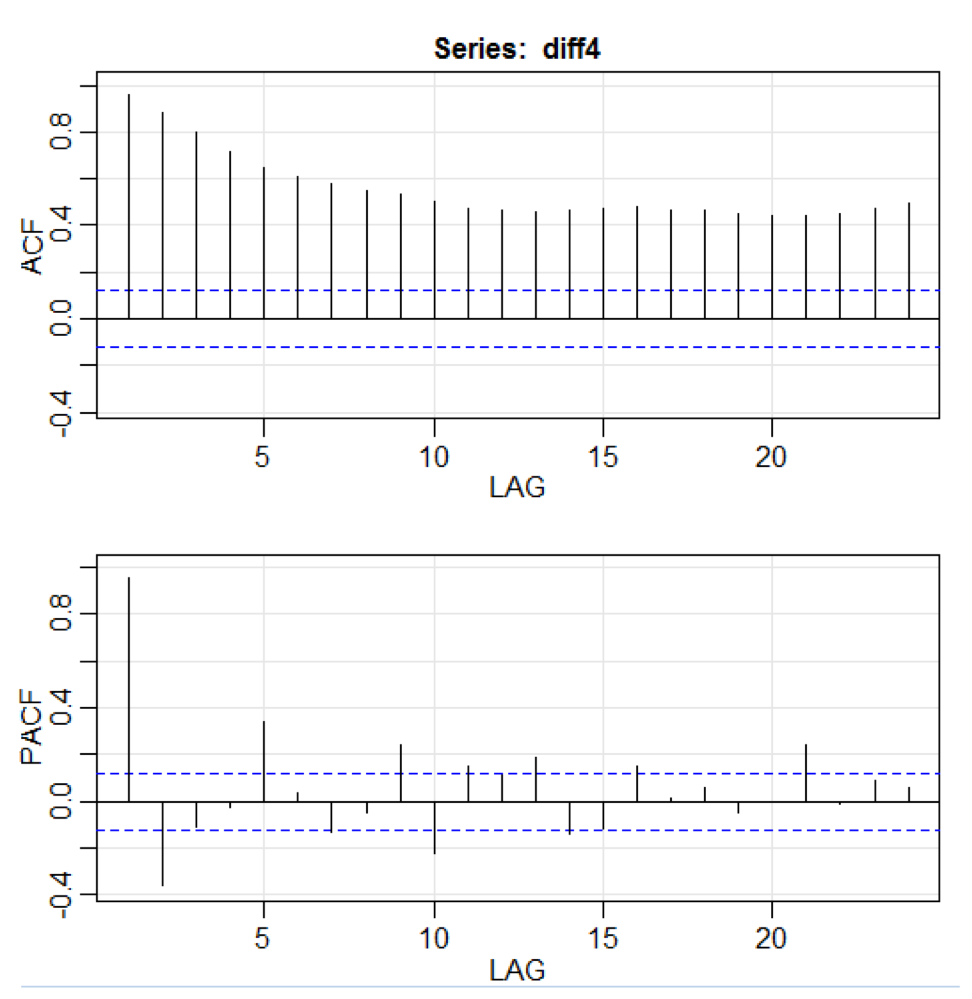
library(astsa) path<-"http://canisius.edu/~yany/RData/" dataSet<-"usGDPquarterly" con<-paste(path,dataSet,".RData",sep='') load(url(con)) x<-.usGDPquarterly$DATE y<-.usGDPquarterly$GDP_CURRENT plot(x,y) diff4 = diff(y,4) acf2(diff4,24)
在上面的代码中,
diff()函数接受差异,例如,当前值减去前一个值。 第二输入值指示延迟。 称为
acf2()的函数用于构建和打印ACF和PACF时间序列。 ACF代表自协方差函数,而PACF代表部分自相关函数。 相关图如下所示:
组件可视化
显然,如果我们可以使用图形,则概念和数据集将更加容易理解。 第一个示例显示了过去五年中美国GDP的波动:
path<-"http://canisius.edu/~yany/RData/" dataSet<-"usGDPannual" con<-paste(path,dataSet,".RData",sep='') load(url(con)) title<-"US GDP" xTitle<-"Year" yTitle<-"US annual GDP" x<-.usGDPannual$YEAR y<-.usGDPannual$GDP plot(x,y,main=title,xlab=xTitle,ylab=yTitle)
相应的时间表如下所示:
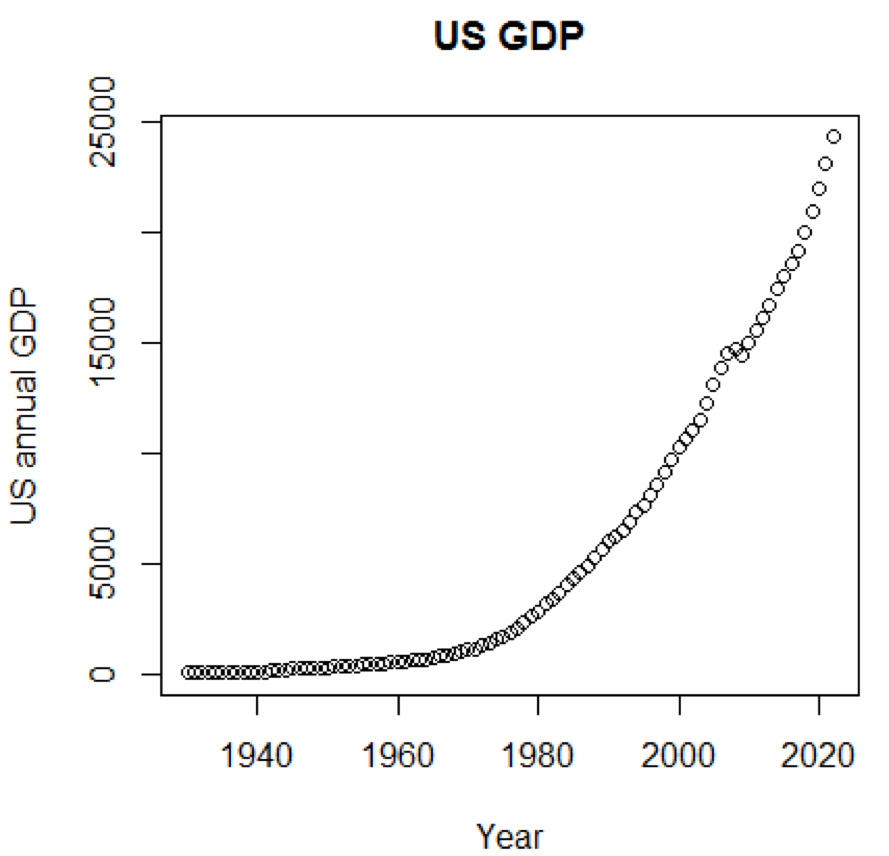
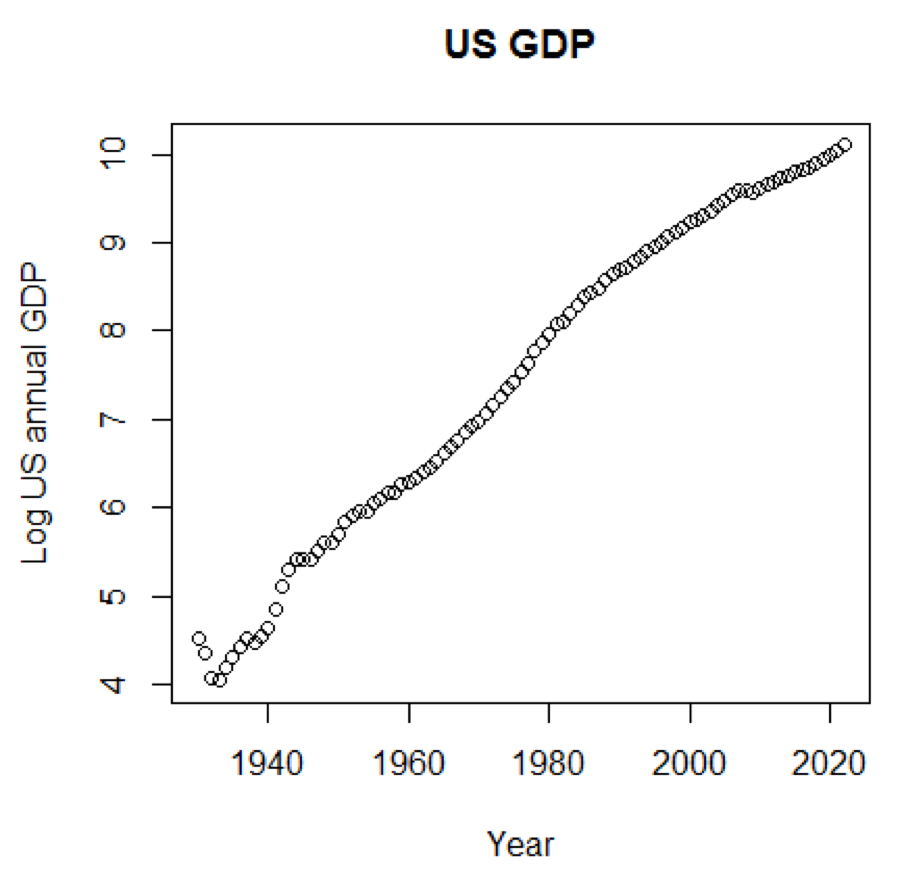
如果我们将对数比例用于GDP,我们将具有以下代码和图形:
yTitle<-"Log US annual GDP" plot(x,log(y),main=title,xlab=xTitle,ylab=yTitle)
下图接近直线:
R包-LiblineaR
该软件包是基于LIBLINEAR C / C ++库的线性预测模型。 这是使用
虹膜数据集的一个示例。 该程序尝试使用训练数据来预测植物属于哪个类别:
library(LiblineaR) data(iris) attach(iris) x=iris[,1:4] y=factor(iris[,5]) train=sample(1:dim(iris)[1],100) xTrain=x[train,];xTest=x[-train,] yTrain=y[train]; yTest=y[-train] s=scale(xTrain,center=TRUE,scale=TRUE)
结论如下。 BCR是平衡的分类率。 对于此投注,越高越好:
cat("Best model type is:",bestType,"\n")
Best model type is: 4
cat("Best cost is:",bestCost,"\n")
Best cost is: 1
cat("Best accuracy is:",bestAcc,"\n")
Best accuracy is: 0.98
print(res) yTest setosa versicolor virginica setosa 16 0 0 versicolor 0 17 0 virginica 0 3 14 print(BCR)
[1] 0.95
R包-eclust
该软件包是面向面向介质的群集,用于高维数据中的解释性预测模型。 首先,让我们看一个名为
simdata的数据集,其中包含一个包的模拟数据:
library(eclust) data("simdata") dim(simdata)
[1] 100 502
simdata[1:5, 1:6]
YE Gene1 Gene2 Gene3 Gene4 [1,] -94.131497 0 -0.4821629 0.1298527 0.4228393 0.36643188 [2,] 7.134990 0 -1.5216289 -0.3304428 -0.4384459 1.57602830 [3,] 1.974194 0 0.7590055 -0.3600983 1.9006443 -1.47250061 [4,] -44.855010 0 0.6833635 1.8051352 0.1527713 -0.06442029 [5,] 23.547378 0 0.4587626 -0.3996984 -0.5727255 -1.75716775
table(simdata[,"E"])
0 1 50 50
先前的结论表明,数据的维数是100 x502。Y是连续响应向量,
E是ECLUST方法的二进制环境变量。
E = 0表示未曝光(n = 50),
E = 1表示曝光(n = 50)。
以下程序R评估Fisher z变换:
library(eclust) data("simdata") X = simdata[,c(-1,-2)] firstCorr<-cor(X[1:50,]) secondCorr<-cor(X[51:100,]) score<-u_fisherZ(n0=100,cor0=firstCorr,n1=100,cor1=secondCorr) dim(score)
[1] 500 500
score[1:5,1:5]
Gene1 Gene2 Gene3 Gene4 Gene5 Gene1 1.000000 -8.062020 6.260050 -8.133437 -7.825391 Gene2 -8.062020 1.000000 9.162208 -7.431822 -7.814067 Gene3 6.260050 9.162208 1.000000 8.072412 6.529433 Gene4 -8.133437 -7.431822 8.072412 1.000000 -5.099261 Gene5 -7.825391 -7.814067 6.529433 -5.099261 1.000000
我们定义了Fisher z变换。 假设我们有一组
n对
x i和
y i ,则可以使用以下公式估算它们的相关性:
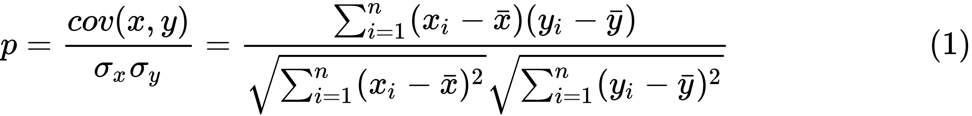
这里
p是两个变量之间的相关性,并且

和
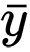
是随机变量
x和
y的样本均值。
z的值定义为:
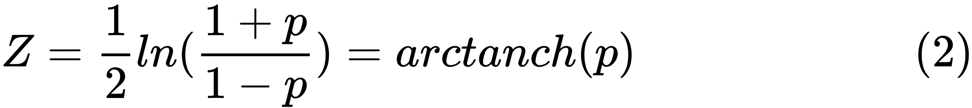 ln
ln是自然对数函数,而
arctanh()是反双曲正切函数。
选型
当找到一个好的模型时,有时我们会面临数据的缺乏/过多。 以下示例是
从此处借用的。 他演示了使用该函数的问题,以及如何使用具有多项式特征的线性回归来近似非线性函数。 指定功能:
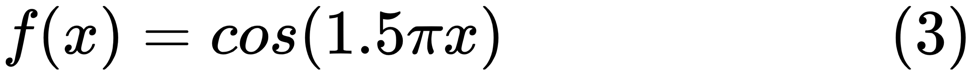
在下一个程序中,我们尝试使用线性和多项式模型来近似方程。 此处显示了经过稍微修改的代码。 该程序说明了数据短缺/供过于求对模型的影响:
import sklearn import numpy as np import matplotlib.pyplot as plt from sklearn.pipeline import Pipeline from sklearn.preprocessing import PolynomialFeatures from sklearn.linear_model import LinearRegression from sklearn.model_selection import cross_val_score
结果图如下所示:
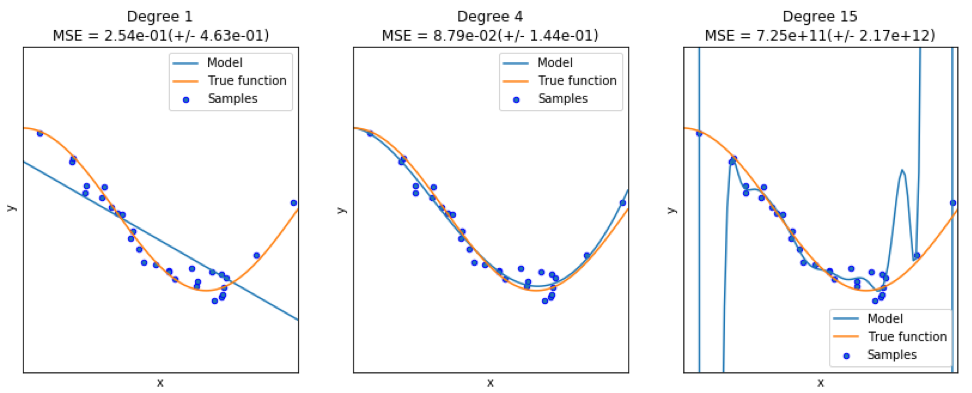
Python程序包-模型走秀
一个例子可以在
这里找到。
代码的前几行如下所示:
import datetime import pandas from sqlalchemy import create_engine from metta import metta_io as metta from catwalk.storage import FSModelStorageEngine, CSVMatrixStore from catwalk.model_trainers import ModelTrainer from catwalk.predictors import Predictor from catwalk.evaluation import ModelEvaluator from catwalk.utils import save_experiment_and_get_hash help(FSModelStorageEngine)
此处显示相应的结论。 为了节省空间,仅显示上部:
Help on class FSModelStorageEngine in module catwalk.storage: class FSModelStorageEngine(ModelStorageEngine) | Method resolution order: | FSModelStorageEngine | ModelStorageEngine | builtins.object | | Methods defined here: | | __init__(self, *args, **kwargs) | Initialize self. See help(type(self)) for accurate signature. | | get_store(self, model_hash) | | ----------------------------------------------------------------------
| Data descriptors inherited from ModelStorageEngine: | | __dict__ | dictionary for instance variables (if defined) | | __weakref__ | list of weak references to the object (if defined)
Python软件包-sklearn
由于
sklearn是一个非常有用的软件包,因此值得展示使用该软件包的更多示例。 此处给出的示例显示了如何使用包使用单词袋方法按主题对文档进行分类。
本示例使用
scipy.sparse矩阵存储对象,并演示了可以有效处理稀疏矩阵的各种分类器。 本示例使用20个新闻组的数据集。 它将自动下载然后缓存。 压缩文件包含输入文件,可以在
此处下载。 该代码可
在此处获得 。 为了节省空间,仅显示前几行:
import logging import numpy as np from optparse import OptionParser import sys from time import time import matplotlib.pyplot as plt from sklearn.datasets import fetch_20newsgroups from sklearn.feature_extraction.text import TfidfVectorizer from sklearn.feature_extraction.text import HashingVectorizer from sklearn.feature_selection import SelectFromModel
相应的输出如下所示:
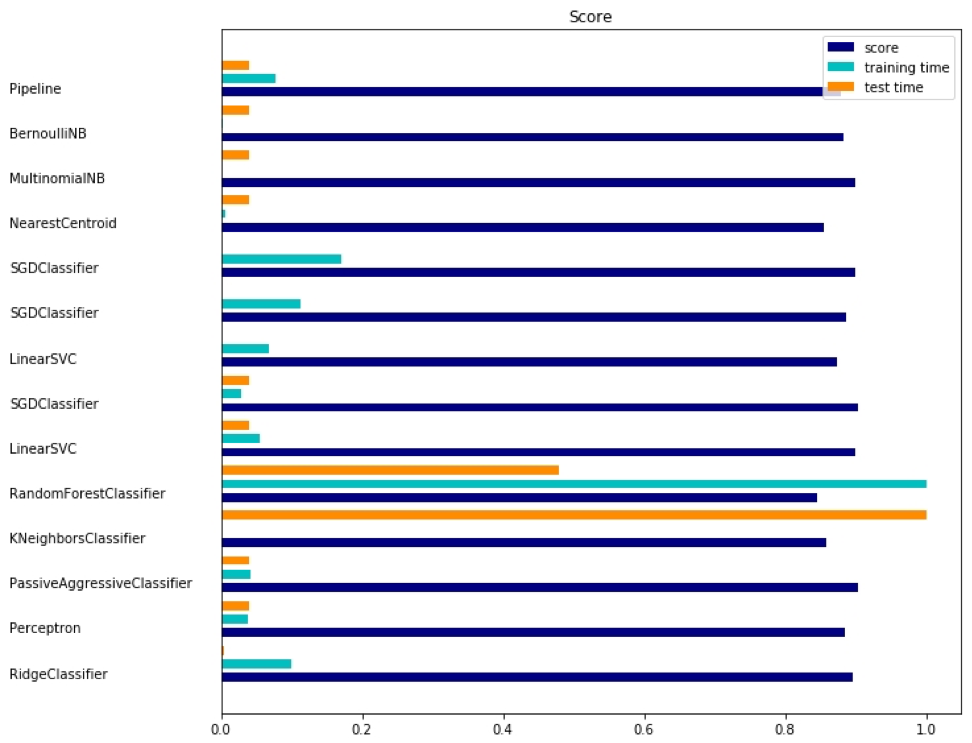
每种方法都有三个指标:评估,培训时间和测试时间。
朱莉娅包-QuantEcon
例如,使用马尔可夫链:
using QuantEcon P = [0.4 0.6; 0.2 0.8]; mc = MarkovChain(P) x = simulate(mc, 100000); mean(x .== 1)
结果:
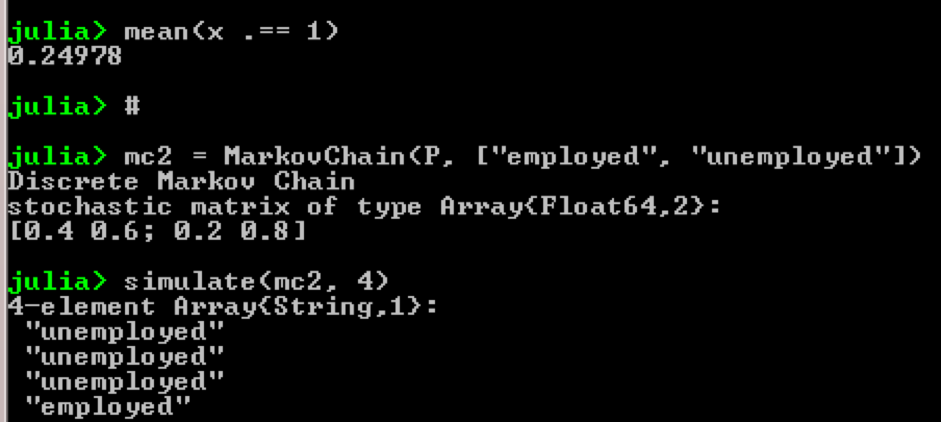
该示例的目的是查看一个人如何从未来的一种经济状况转变为另一种经济状况。 首先,让我们看一下下面的图表:
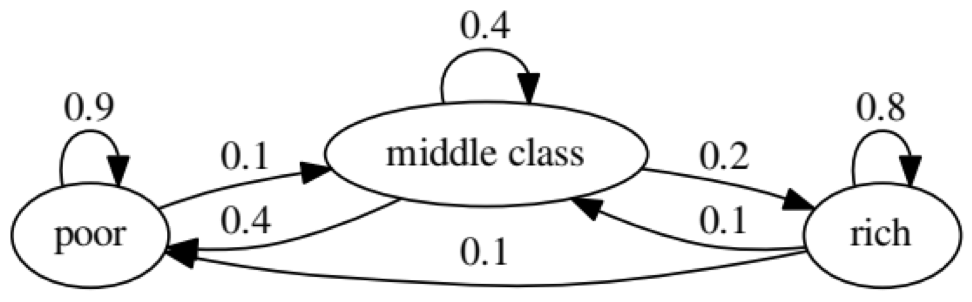
让我们看一下状态最差的最左侧的椭圆形。 0.9表示具有此地位的人有90%的机会变得贫穷,而10%的人进入中产阶级。 它可以由以下矩阵表示,零是节点之间没有边的位置:
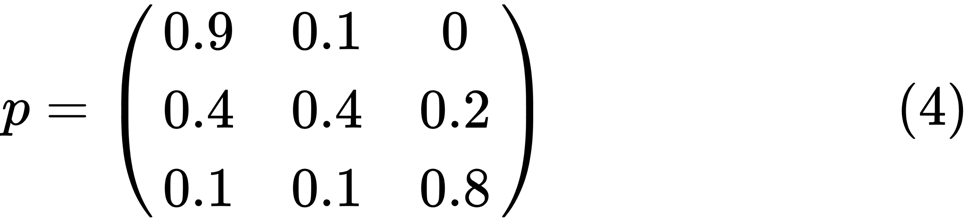
据说,如果存在正整数j和k,则两个状态x和y相互关联,例如:

如果所有状态都连通,则马尔可夫链
P称为不可约链; 也就是说,如果每个(x,y)
都报告了
x和
y 。 以下代码将确认这一点:
using QuantEcon P = [0.9 0.1 0.0; 0.4 0.4 0.2; 0.1 0.1 0.8]; mc = MarkovChain(P) is_irreducible(mc)
下图是一个极端的情况,因为穷人的未来状况将是100%的贫困:

以下代码也将对此进行确认,因为结果将为
false :
using QuantEcon P2 = [1.0 0.0 0.0; 0.1 0.8 0.1; 0.0 0.2 0.8]; mc2 = MarkovChain(P2) is_irreducible(mc2)
格兰杰因果检验
格兰杰因果关系检验用于确定一个时间序列是否是一个因素,并为预测第二个时间序列提供有用的信息。 以下代码以名为
ChickEgg的
数据集为例。 数据集有两列,鸡的数量和卵的数量,并带有时间戳:
library(lmtest) data(ChickEgg) dim(ChickEgg)
[1] 54 2
ChickEgg[1:5,]
chicken egg [1,] 468491 3581 [2,] 449743 3532 [3,] 436815 3327 [4,] 444523 3255 [5,] 433937 3156
问题是,我们可以利用今年的鸡蛋数量来预测明年的鸡数量吗?
如果是这样,那么鸡的数量将成为格兰杰鸡蛋数量的原因。 如果不是这种情况,我们就说鸡的数量并不是鸡蛋数量的格兰杰原因。 以下是相关代码:
library(lmtest) data(ChickEgg) grangertest(chicken~egg, order = 3, data = ChickEgg)
Granger causality test Model 1: chicken ~ Lags(chicken, 1:3) + Lags(egg, 1:3) Model 2: chicken ~ Lags(chicken, 1:3) Res.Df Df F Pr(>F) 1 44 2 47 -3 5.405 0.002966 ** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
在模型1中,我们尝试使用雏鸡滞后加卵子滞后来解释雏鸡的数量。
因为
P的值很小(在0.01处有显着性),我们说鸡蛋的数量是鸡数量的格兰杰原因。
以下测试表明,有关鸡的数据不能用于预测以下时期:
grangertest(egg~chicken, order = 3, data = ChickEgg)
Granger causality test Model 1: egg ~ Lags(egg, 1:3) + Lags(chicken, 1:3) Model 2: egg ~ Lags(egg, 1:3) Res.Df Df F Pr(>F) 1 44 2 47 -3 0.5916 0.6238
在以下示例中,我们检查了IBM和S&P500的获利能力,以找出它们是另一个的格兰杰原因。
首先,我们定义yield函数:
ret_f<-function(x,ticker=""){ n<-nrow(x) p<-x[,6] ret<-p[2:n]/p[1:(n-1)]-1 output<-data.frame(x[2:n,1],ret) name<-paste("RET_",toupper(ticker),sep='') colnames(output)<-c("DATE",name) return(output) }
>x<-read.csv("http://canisius.edu/~yany/data/ibmDaily.csv",header=T) ibmRet<-ret_f(x,"ibm") x<-read.csv("http://canisius.edu/~yany/data/^gspcDaily.csv",header=T) mktRet<-ret_f(x,"mkt") final<-merge(ibmRet,mktRet) head(final)
DATE RET_IBM RET_MKT 1 1962-01-03 0.008742545 0.0023956877 2 1962-01-04 -0.009965497 -0.0068887673 3 1962-01-05 -0.019694350 -0.0138730891 4 1962-01-08 -0.018750380 -0.0077519519 5 1962-01-09 0.011829467 0.0004340133 6 1962-01-10 0.001798526 -0.0027476933
现在可以使用输入值调用该函数。 该计划的目的是测试我们是否可以利用市场滞后来解释IBM的盈利能力。 同样,我们检查以解释IBM在市场收入方面的滞后:
library(lmtest) grangertest(RET_IBM ~ RET_MKT, order = 1, data =final)
Granger causality test Model 1: RET_IBM ~ Lags(RET_IBM, 1:1) + Lags(RET_MKT, 1:1) Model 2: RET_IBM ~ Lags(RET_IBM, 1:1) Res.Df Df F Pr(>F) 1 14149 2 14150 -1 24.002 9.729e-07 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
结果表明,S&P500可以用来解释IBM下一时期的盈利能力,因为它具有0.1%的统计显着性。 以下代码将检查IBM的滞后是否解释了S&P500中的更改:
grangertest(RET_MKT ~ RET_IBM, order = 1, data =final)
Granger causality test Model 1: RET_MKT ~ Lags(RET_MKT, 1:1) + Lags(RET_IBM, 1:1) Model 2: RET_MKT ~ Lags(RET_MKT, 1:1) Res.Df Df F Pr(>F) 1 14149 2 14150 -1 7.5378 0.006049 ** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
结果表明,在此期间,IBM的收益可用于解释下一时期的S&P500指数。