前言

在本文中,我们将探讨SVM的几个方面:
- 支持向量机的理论组成;
- 该算法如何处理无法线性划分为多个类别的样本;
- SciKit学习库中的Python示例和该算法的实现。
在以下文章中,我将尝试讨论该算法的数学组成部分。
如您所知,机器学习任务分为两大类-分类和回归。 根据我们要面对的这些任务以及该任务具有的数据集,我们选择要使用的算法。
支持向量机方法或SVM(来自英语支持向量机)是用于分类和回归问题的线性算法。 该算法在实践中得到了广泛的应用,可以解决线性和非线性问题。 支持向量的“机器”的本质很简单:该算法创建一条线或超平面,将数据分为几类。
理论
该算法的主要任务是找到最正确的线或超平面,将数据分为两类。 SVM是一种在输入端接收数据并返回此类分界线的算法。
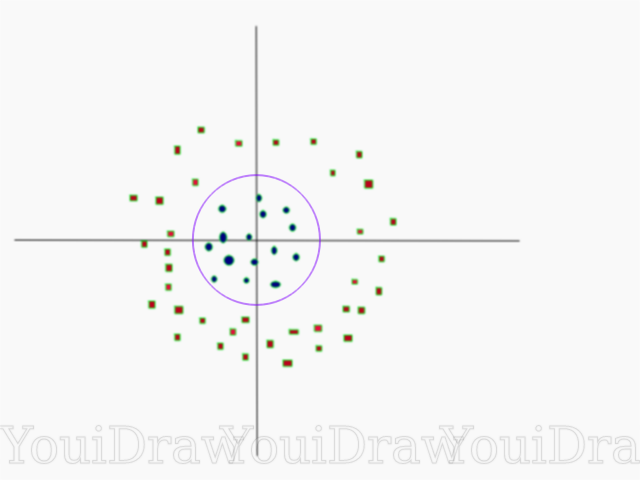
考虑以下示例。 假设我们有一个数据集,我们想将红色方块与蓝色圆圈进行分类和分离(假设是正数和负数)。 此任务的主要目标是找到将这两个类分开的“理想”行。
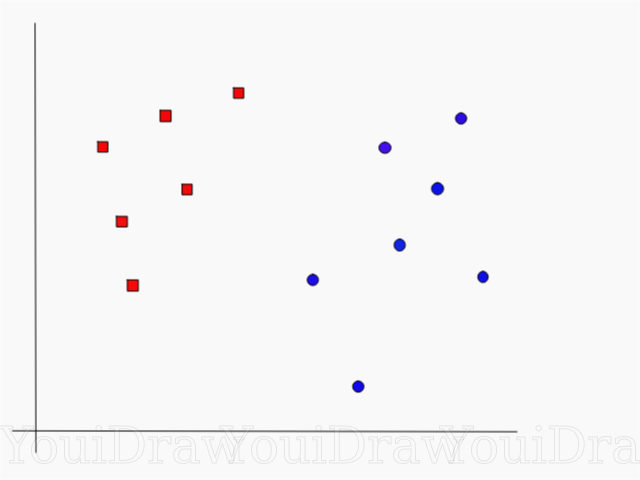
找到将数据集分为蓝色和红色类别的理想线或超平面。
乍一看,并不难,对吧?
但是,正如您所看到的,没有一个独特的解决方案可以解决这一问题。 我们可以选择无数行来分隔这两个类。 SVM如何准确地找到“理想”路线,以及在其理解中什么是“理想”?
请看下面的示例,并认为两条线(黄色或绿色)中哪一条最能区分这两个类别,并适合“理想”的描述?
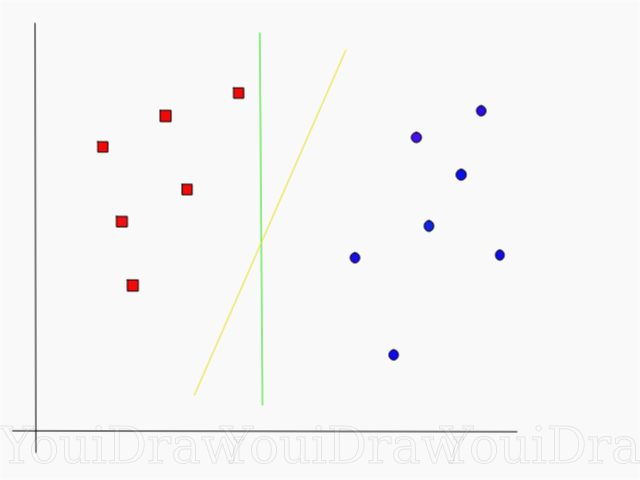
您认为哪条线更好地分隔了数据集?
如果您选择了黄线,则表示祝贺:这是算法将选择的线。 在此示例中,我们可以直观地了解到,黄线分开,因此对这两个类别的分类要比绿色类别更好。
如果是绿线-距离红线太近了。 尽管她正确地对当前数据集的所有对象进行了分类,但这样的行将不会被概括化-对于不熟悉的数据集,它的表现将不会很好。 查找广义的将两类分开的任务是机器学习的主要任务之一。
SVM如何找到最佳路线
SVM算法的设计方式是,它搜索图上直接位于最接近分隔线的点。 这些点称为参考向量。 然后,该算法计算支持向量与分割平面之间的距离。 这就是称为间隙的距离。 该算法的主要目标是最大化间隙距离。 最佳超平面被认为是其间隙尽可能大的超平面。

很简单,对吧? 考虑以下示例,该示例具有无法线性划分的更复杂的数据集。
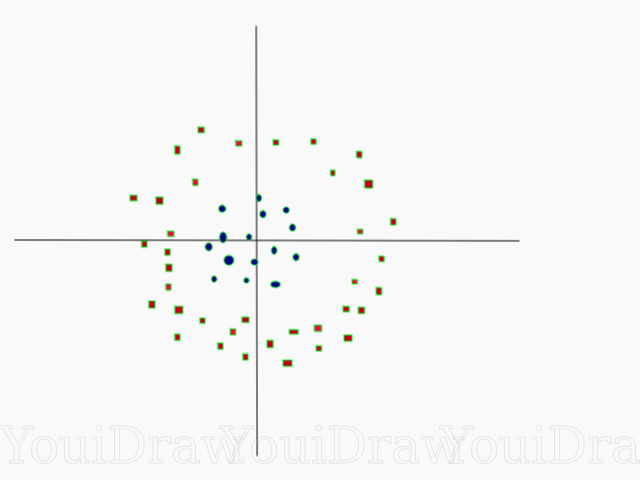
显然,该数据集不能线性划分。 我们无法画出可以对这些数据进行分类的直线。 但是,可以通过添加一个额外的维度(我们称为Z轴)来线性划分该数据集,想象一下Z轴上的坐标受以下限制:
因此,纵坐标Z是从点到轴起点的距离的平方表示的。
下面是Z轴上相同数据集的可视化。
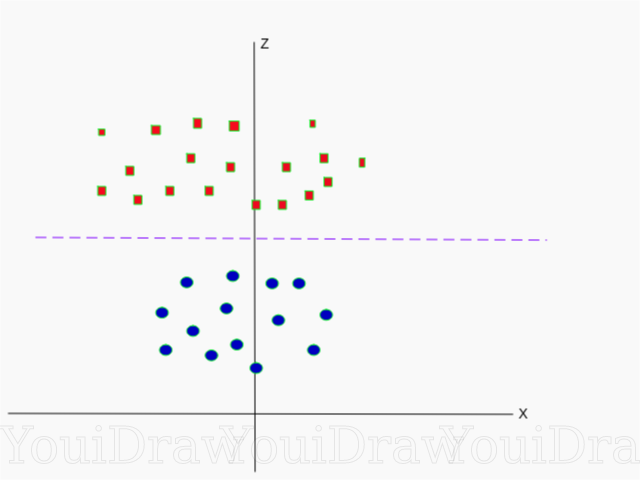
现在,数据可以线性划分了。 假设洋红色线分隔数据z = k,其中k为常数。 如果
然后
-圆公式。 因此,我们可以使用此变换将线性除法器投影回到样本尺寸的原始数量。
结果,我们可以通过为非线性数据集添加一个附加维度来对其进行分类,然后使用数学转换将其恢复为原始形式。 但是,并非所有数据集都容易进行这种转换。 幸运的是,该算法在sklearn库中的实现为我们解决了这个问题。
超飞机
既然我们已经熟悉了算法的逻辑,那么我们将继续进行超平面的正式定义
超平面是n维欧氏空间中的n-1维子平面,它将空间分成两个单独的部分。
例如,假设我们的线表示为一维欧几里得空间(即我们的数据集位于一条直线上)。 在这条线上选择一个点。 这一点会将数据集(在我们的情况下为该行)分为两部分。 线有1个小节,而点有0个小节。 因此,点是直线的超平面。
对于我们之前遇到的二维数据集,分界线是同一超平面。 简而言之,对于一个n维空间,存在一个n-1维超平面,将该空间分为两部分。
代码
import numpy as np X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]]) y = np.array([1, 1, 2, 2])
点表示为X的数组,点所属的类表示为y的数组。
现在,我们将使用该样本训练模型。 对于此示例,我设置了分类器(内核)的“内核”的线性参数。
from sklearn.svm import SVC clf = SVC(kernel='linear') clf = SVC.fit(X, y)
新对象的类别预测
prediction = clf.predict([[0,6]])
参数设定
参数是您在创建分类器时传递的参数。 下面,我提供了一些最重要的自定义SVM设置:
“ C”此参数有助于调整“平滑度”与训练样本中对象分类的准确性之间的细线。 “ C”值越高,训练集中的对象将被正确分类。

在此示例中,我们可以为此特定样本定义几个决策阈值。 注意直接(在图表上显示为绿线)决策阈值。 这非常简单,因此,几个对象的分类不正确。 这些未正确分类的点在数据中称为离群值。
我们还可以调整参数,以使最终得到一条更弯曲的线(浅蓝色决策阈值),这将对所有训练样本数据进行绝对分类。 当然,在这种情况下,我们的模型将能够推广并在新数据上显示出同样好的结果的机会非常小。 因此,如果您在训练模型时尝试达到准确性,则应该追求更均匀,直接的目标。 “ C”数越高,超平面在模型中的纠缠度就越高,但是训练集中正确分类的对象的数目就越高。 因此,重要的是“扭曲”特定数据集的模型参数,以避免再训练,但同时又要达到很高的精度。
伽玛在官方文档中,SciKit Learn库表示,伽玛确定数据集中每个元素对确定“理想线”的影响程度。 伽玛值越低,则更多的元素(即使距离分隔线足够远的元素)也参与选择该线的过程。 如果伽马系数很高,则算法将仅“依赖”最接近直线本身的那些元素。
如果伽马级别设置得太高,则只有最接近直线的元素才会参与直线位置的决策过程。 这将有助于忽略数据中的异常值。 SVM算法经过精心设计,以使决策时彼此最接近的点具有更大的权重。 但是,使用正确的“ C”和“ gamma”设置,可以获得获得最佳结果,该结果将构建一个更线性的超平面,从而忽略异常值,因此更具通用性。
结论
我衷心希望本文能帮助您了解SVM或参考矢量方法的本质。 我希望您有任何意见和建议。 在随后的出版物中,我将讨论SVM的数学组成部分和优化问题。
资料来源:
SciKit学习中的官方SVM文档TowardsDataScience博客Siraj Raval:支持向量机机器学习Udacity SVM入门:Gamma课程视频维基百科:SVM