来源 ：Wikipedia许可CC-BY-SA 3.0

如果您经常乘坐公共交通工具旅行，您可能会遇到这种情况：

你停下来。 据记载，公交车每10分钟运行一次。 注意时间...终于，在11分钟后，公交车到达了，并产生了一个想法：为什么我总是不走运？

从理论上讲，如果公交车每10分钟到达一次，而您是随机到达的，则平均等待时间应为5分钟左右。 但实际上，公交车无法按时到达，因此您可以等待更长的时间。 事实证明，通过一些合理的假设，可以得出一个惊人的结论：

当您等待平均每10分钟一班的公共汽车时，您的平均等待时间将为10分钟。

这就是有时所说的等待时间悖论 。

我以前有一个主意，我一直想知道这是否真的是……这种“合理的假设”与现实有多少对应？ 在本文中，我们从建模和概率论的角度研究了延迟悖论，然后看了一些真实的西雅图巴士数据，以（希望）彻底解决这一悖论。

悖论检查

如果公交车恰好每十分钟一班，那么平均等待时间将是5分钟。 可以很容易地理解为什么增加公交车间隔的间隔会增加平均等待时间。

等待时间悖论是一种更普遍的现象的特殊情况- 检查悖论 ，在艾伦·唐尼（ Allen Downey ）的明智文章“我们周围的检查悖论”中进行了详细讨论。

简而言之，每当观察数量的概率与观察到的数量相关时，就会出现检查悖论。 艾伦举了一个关于大学生平均班级规模的调查示例。 尽管学校确实说出了一组中30名学生的平均人数， 但从学生的角度来看 ，平均组人数要大得多。 原因是在大班中（自然地）有更多的学生，这在他们的调查中显示出来。

对于声明的10分钟间隔的公交时刻表，有时到达之间的间隔大于10分钟，有时更短。 而且，如果您在随机的时间停下来，那么遇到间隔的时间要比间隔的时间短。 因此，合乎逻辑的是， 等待时间间隔之间的平均时间间隔要比总线之间的平均时间间隔长，因为更长的时间间隔在样本中更为常见。

但是延迟悖论提出了一个更强有力的声明：如果平均总线间隔为 $$$N$ 分钟， 旅客平均等待时间为 $$$2N$ 分钟。 这是真的吗？

延迟模拟

为了使自己信服，我们首先模拟了平均在10分钟内到达的公交车流量。 为了提高准确性，请抽样：一百万辆公交车（或大约19年的全天候10分钟流量）：

import numpy as np N = 1000000 # number of buses tau = 10 # average minutes between arrivals rand = np.random.RandomState(42) # universal random seed bus_arrival_times = N * tau * np.sort(rand.rand(N)) 

检查平均间隔是否接近 $$$\ tau = 10$ ：

 intervals = np.diff(bus_arrival_times) intervals.mean() 

9.9999879601518398

现在，我们可以模拟这段时间内大量乘客到达公交车站的路程，并计算每个乘客所经历的等待时间。 将代码封装在函数中以供以后使用：

 def simulate_wait_times(arrival_times, rseed=8675309, # Jenny's random seed n_passengers=1000000): rand = np.random.RandomState(rseed) arrival_times = np.asarray(arrival_times) passenger_times = arrival_times.max() * rand.rand(n_passengers) # find the index of the next bus for each simulated passenger i = np.searchsorted(arrival_times, passenger_times, side='right') return arrival_times[i] - passenger_times 

然后我们模拟等待时间并计算平均值：

 wait_times = simulate_wait_times(bus_arrival_times) wait_times.mean() 

10.001584206227317

矛盾的是，平均等待时间接近10分钟。

深入研究：概率和泊松过程

如何模拟这种情况？

实际上，这是检验悖论的一个示例，其中观察值的概率与值本身有关。 表示为 $$$p（T）$ 间距 $$$T$ 到达巴士站时在巴士之间。 在这样的记录中，到达时间的期望值为：

$$

$$E [T] = \ int_0 ^ \ infty T〜p（T）〜dT$$

在先前的模拟中，我们选择了 $$$E [T] = \ tau = 10$ 分钟。

当乘客随时到达公交车站时，等待时间的可能性不仅取决于 $$$p（T）$ 而且来自 $$$T$ ：间隔越大，其中的乘客越多。

因此，我们可以从乘客的角度写出到达时间的分布：

$$

$$p_ {exp}（T）\原始T〜p（T）$$

比例常数由分布的归一化得出：

$$

$$p_ {exp}（T）= \ frac {T〜p（T）} {\ int_0 ^ \ infty T〜p（T）〜dT}$$

它简化为

$$

$$p_ {exp}（T）= \ frac {T〜p（T）} {E [T]}$$

然后等待时间 $$$E [W]$ 将是乘客预期间隔的一半，因此我们可以记录

$$

$$E [W] = \ frac {1} {2} E_ {exp} [T] = \ frac {1} {2} \ int_0 ^ \ infty T〜p_ {exp}（T）〜dT$$

可以用更容易理解的方式重写它：

$$

$$E [W] = \ frac {E [T ^ 2]} {2E [T]}$$

现在只剩下选择一种形式了 $$$p（T）$ 并计算积分。

p（T）的选择

收到正式模型后，什么是合理的分配 $$$p（T）$ ？ 我们将绘制分布图 $$$p（T）$ 通过绘制两次到达间隔的直方图，在我们的模拟到达范围内：

 %matplotlib inline import matplotlib.pyplot as plt plt.style.use('seaborn') plt.hist(intervals, bins=np.arange(80), density=True) plt.axvline(intervals.mean(), color='black', linestyle='dotted') plt.xlabel('Interval between arrivals (minutes)') plt.ylabel('Probability density'); 

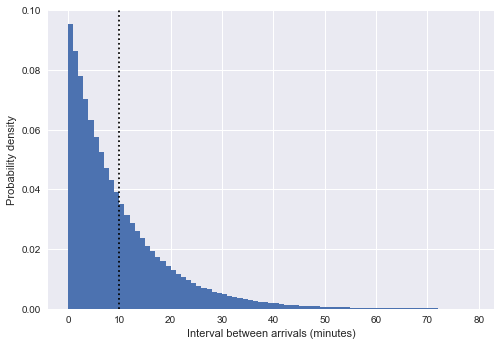
在此，垂直虚线表示大约10分钟的平均间隔。 这非常类似于指数分布，并非偶然：我们以均匀随机数形式对公交车到达时间的仿真非常接近泊松过程 ，对于这种过程，间隔的分布是指数的。

（注意：在我们的例子中，这只是一个近似指数；实际上，间隔 $$$T$ 介于 $$$N$ 在一个时间段内均匀选择的点 $$$N \ tau$ 符合Beta版本 $$$T /（N \ tau）\ sim \ mathrm {Beta} [1，N]$ 这是最大的 $$$N$ 接近 $$$T \ sim \ mathrm {Exp} [1 / / tau]$ 。 有关更多信息，您可以阅读例如StackExchange上的帖子或Twitter上的该 主题 。

间隔的指数分布意味着到达时间遵循泊松过程。 为了验证这种推理，我们检查了泊松过程的另一个属性的存在：在固定时间段内到达的次数是泊松分布。 为此，我们将模拟的到达时间划分为多个时间段：

 from scipy.stats import poisson # count the number of arrivals in 1-hour bins binsize = 60 binned_arrivals = np.bincount((bus_arrival_times // binsize).astype(int)) x = np.arange(20) # plot the results plt.hist(binned_arrivals, bins=x - 0.5, density=True, alpha=0.5, label='simulation') plt.plot(x, poisson(binsize / tau).pmf(x), 'ok', label='Poisson prediction') plt.xlabel('Number of arrivals per hour') plt.ylabel('frequency') plt.legend(); 

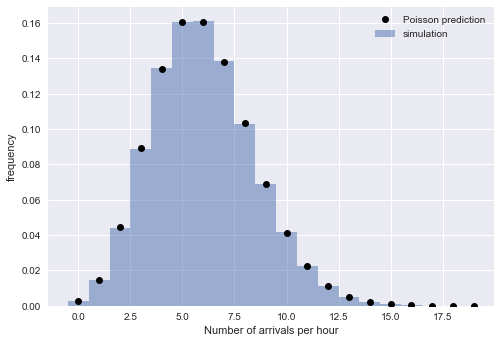
经验值和理论值的紧密对应关系使我们相信我们的解释的正确性： $$$N$ 泊松过程很好地描述了模拟的到达时间，这意味着指数分布的间隔。

这意味着概率分布可以写成：

$$

$$p（T）= \ frac {1} {\ tau} e ^ {-T / \ tau}$$

如果将结果替换为先前的公式，我们将找到车站的乘客平均等待时间：

$$

$$E [W] = \ frac {\ int_0 ^ \ infty T ^ 2〜e ^ {-T / \ tau}} {2 \ int_0 ^ \ infty T〜e ^ {-T / \ tau}} = \ frac {2 \ tau ^ 3} {2（\ tau ^ 2）} = \ tau$$

对于通过泊松过程到达的航班，预期的等待时间等于两次到达之间的平均间隔。

这个问题可以说是：泊松过程是一个没有记忆的过程，也就是说，事件的历史与下一个事件的预期时间无关。 因此，到达公共汽车站时，公共汽车的平均等待时间始终是相同的：在我们的示例中，这是10分钟，无论自上次公共汽车经过了多长时间！ 您等待了多长时间都没有关系：到下一班车的预期时间总是恰好是10分钟：在泊松过程中，您所花费的等待时间不会得到“积分”。

现实超时

如果真正的公交车到站实际上是由Poisson过程描述的，那么上面的方法很好，但是是这样吗？


资料来源： 西雅图公共交通计划

让我们尝试确定等待时间的悖论如何与现实保持一致。 为此，我们将在此处检查一些可下载的数据： arrival_times.csv （3 MB CSV文件）。 该数据集包含西雅图市中心第3和派克巴士站的RapidRide巴士C，D和E的计划到达时间和实际到达时间。 该数据记录在2016年第二季度（非常感谢华盛顿州运输中心的Mark Hallenback提供了此文件！）。

 import pandas as pd df = pd.read_csv('arrival_times.csv') df = df.dropna(axis=0, how='any') df.head() 

	OPD_DATE	VEHICLE_ID	RTE	目录	TRIP_ID	STOP_ID	STOP_NAME	SCH_STOP_TM	ACT_STOP_TM
0	2016-03-26	6201	673	小号	30908177	431	3RD AVE＆PIKE ST（431）	01:11:57	01:13:19
1个	2016-03-26	6201	673	小号	30908033	431	3RD AVE＆PIKE ST（431）	23:19:57	23:16:13
2	2016-03-26	6201	673	小号	30908028	431	3RD AVE＆PIKE ST（431）	21:19:57	21:18:46
3	2016-03-26	6201	673	小号	30908019	431	3RD AVE＆PIKE ST（431）	19:04:57	19:01:49
4	2016-03-26	6201	673	小号	30908252	431	3RD AVE＆PIKE ST（431）	16:42:57	16:42:39

我选择了RapidRide数据，包括因为在一天中大部分时间里公交车以10-15分钟的固定间隔运行，更不用说我是C线的常客。

数据清理

首先，我们将进行一些数据清理以将其转换为方便的视图：

 # combine date and time into a single timestamp df['scheduled'] = pd.to_datetime(df['OPD_DATE'] + ' ' + df['SCH_STOP_TM']) df['actual'] = pd.to_datetime(df['OPD_DATE'] + ' ' + df['ACT_STOP_TM']) # if scheduled & actual span midnight, then the actual day needs to be adjusted minute = np.timedelta64(1, 'm') hour = 60 * minute diff_hrs = (df['actual'] - df['scheduled']) / hour df.loc[diff_hrs > 20, 'actual'] -= 24 * hour df.loc[diff_hrs < -20, 'actual'] += 24 * hour df['minutes_late'] = (df['actual'] - df['scheduled']) / minute # map internal route codes to external route letters df['route'] = df['RTE'].replace({673: 'C', 674: 'D', 675: 'E'}).astype('category') df['direction'] = df['DIR'].replace({'N': 'northbound', 'S': 'southbound'}).astype('category') # extract useful columns df = df[['route', 'direction', 'scheduled', 'actual', 'minutes_late']].copy() df.head() 

	路线	方向	图表	事实 到达	迟滞（分钟）
0	ç	南边	2016-03-26 01:11:57	2016-03-26 01:13:19	1.366667
1个	ç	南边	2016-03-26 23:19:57	2016-03-26 23:16:13	-3.733333
2	ç	南边	2016-03-26 21:19:57	2016-03-26 21:18:46	-1.183333
3	ç	南边	2016-03-26 19:04:57	2016-03-26 19:01:49	-3.133333
4	ç	南边	2016-03-26 16:42:57	2016-03-26 16:42:39	-0.300000

公共汽车多晚？

该表中有6个数据集：每个路线C，D和E的南北方向。为了了解它们的特性，让我们为这6个路线中的每一个建立实际减去计划到达时间的直方图：

 import seaborn as sns g = sns.FacetGrid(df, row="direction", col="route") g.map(plt.hist, "minutes_late", bins=np.arange(-10, 20)) g.set_titles('{col_name} {row_name}') g.set_axis_labels('minutes late', 'number of buses'); 

合理的假设是，公交车在路线的起点更接近时间表，而在路线终点则偏离更多。 数据证实了这一点：我们在南部路线C以及在北部D和E处的停靠站靠近路线的起点，并且方向相反，距离最终目的地不远。

计划和观察间隔

查看这六个路线的已观察到的和计划的公交车间隔。 让我们从Pandas中的groupby函数开始计算这些间隔：

 def compute_headway(scheduled): minute = np.timedelta64(1, 'm') return scheduled.sort_values().diff() / minute grouped = df.groupby(['route', 'direction']) df['actual_interval'] = grouped['actual'].transform(compute_headway) df['scheduled_interval'] = grouped['scheduled'].transform(compute_headway) 

 g = sns.FacetGrid(df.dropna(), row="direction", col="route") g.map(plt.hist, "actual_interval", bins=np.arange(50) + 0.5) g.set_titles('{col_name} {row_name}') g.set_axis_labels('actual interval (minutes)', 'number of buses'); 

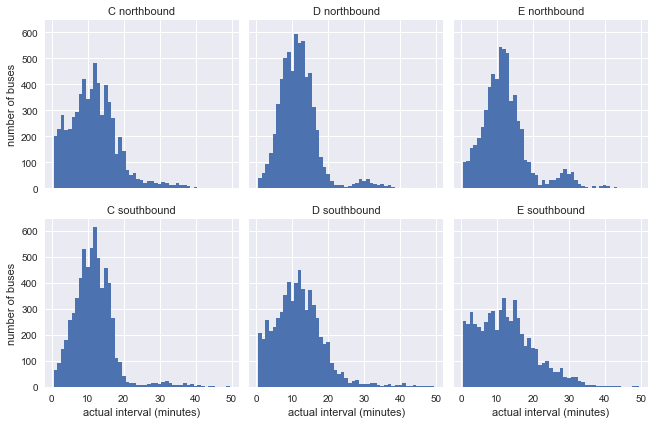
已经很明显，结果与我们的模型的指数分布并不十分相似，但这仍然没有说明什么：分布可能受到图中不一致间隔的影响。

让我们以计划的而不是观察的到达间隔重复图的构造：

 g = sns.FacetGrid(df.dropna(), row="direction", col="route") g.map(plt.hist, "scheduled_interval", bins=np.arange(20) - 0.5) g.set_titles('{col_name} {row_name}') g.set_axis_labels('scheduled interval (minutes)', 'frequency'); 

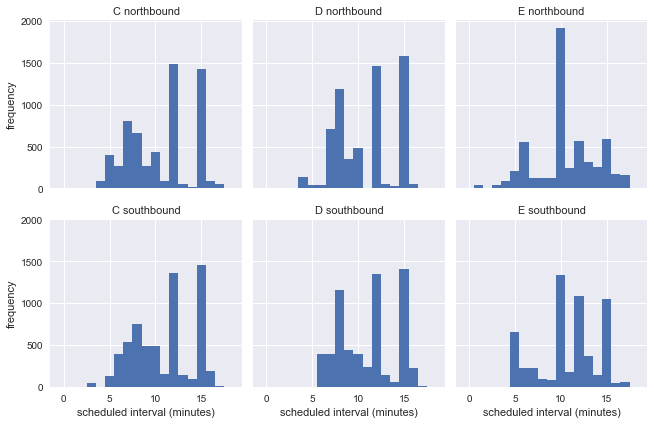
这表明公交车在一周中以不同的间隔运行，因此我们无法使用公交车站的实际信息来估算等待时间悖论的准确性。

建立统一的时间表

尽管官方时间表没有给出统一的时间间隔，但是有一些特定的时间间隔，其中有大量的公交车：例如，向北行驶的大约2000辆E线公交车，计划的间隔时间为10分钟。 为了找出延迟悖论是否适用，让我们将数据分组为路线，方向和计划的时间间隔，然后将它们重新堆叠，就好像它们是顺序发生的一样。 这应保留源数据的所有相关特征，同时便于与潜伏期悖论的预测进行直接比较。

 def stack_sequence(data): # first, sort by scheduled time data = data.sort_values('scheduled') # re-stack data & recompute relevant quantities data['scheduled'] = data['scheduled_interval'].cumsum() data['actual'] = data['scheduled'] + data['minutes_late'] data['actual_interval'] = data['actual'].sort_values().diff() return data subset = df[df.scheduled_interval.isin([10, 12, 15])] grouped = subset.groupby(['route', 'direction', 'scheduled_interval']) sequenced = grouped.apply(stack_sequence).reset_index(drop=True) sequenced.head() 

	路线	方向	日程安排	事实 到达	迟滞（分钟）	事实 间隔	预定间隔
0	ç	北	10.0	12.400000	2,400,000	N	10.0
1个	ç	北	20.0	27.150000	7.150000	0.183333	10.0
2	ç	北	30.0	26.966667	-3.033333	14.566667	10.0
3	ç	北	40.0	35.516667	-4.483333	8.366667	10.0
4	ç	北	50.0	53.583333	3.583333	18.066667	10.0

在清除的数据上，您可以绘制公交车沿每个路线和方向的实际外观分布图，并以到达频率为单位：

 for route in ['C', 'D', 'E']: g = sns.FacetGrid(sequenced.query(f"route == '{route}'"), row="direction", col="scheduled_interval") g.map(plt.hist, "actual_interval", bins=np.arange(40) + 0.5) g.set_titles('{row_name} ({col_name:.0f} min)') g.set_axis_labels('actual interval (min)', 'count') g.fig.set_size_inches(8, 4) g.fig.suptitle(f'{route} line', y=1.05, fontsize=14) 

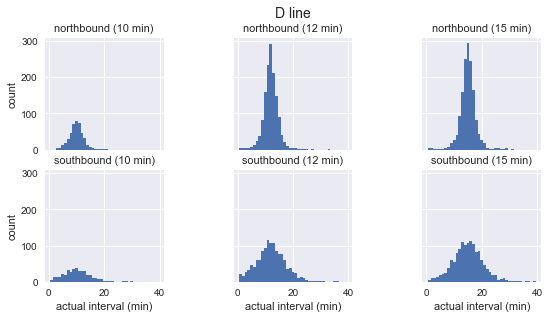
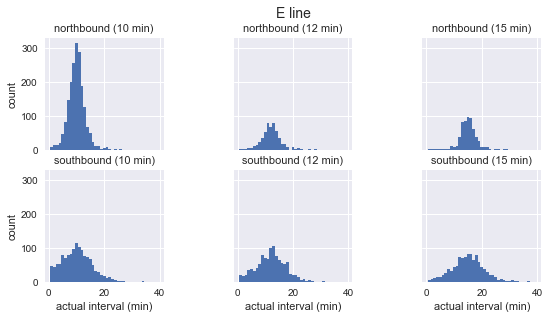
我们看到，对于每条路线，观察到的间隔的分布几乎都是高斯分布。 它在计划的时间间隔附近达到峰值，标准差在路线开始时较小（C为南，D / E为北）在结束时更大。 即使从视觉上看，实际到达间隔也绝对不对应于指数分布，这是等待时间悖论的主要假设。

我们可以使用上面使用的等待时间模拟功能来找到每条公交路线，方向和时间表的平均等待时间：

 grouped = sequenced.groupby(['route', 'direction', 'scheduled_interval']) sims = grouped['actual'].apply(simulate_wait_times) sims.apply(lambda times: "{0:.1f} +/- {1:.1f}".format(times.mean(), times.std())) 

 路线方向预定时间间隔
 C北10.0 7.8 +/- 12.5
                       12.0 7.4 +/- 5.7
                       15.0 8.8 +/- 6.4
         南10.0 6.2 +/- 6.3
                       12.0 6.8 +/- 5.2
                       15.0 8.4 +/- 7.3
 D北10.0 6.1 +/- 7.1
                       12.0 6.5 +/- 4.6
                       15.0 7.9 +/- 5.3
         南10.0 6.7 +/- 5.3
                       12.0 7.5 +/- 5.9
                       15.0 8.8 +/- 6.5
 E北10.0 5.5 +/- 3.7
                       12.0 6.5 +/- 4.3
                       15.0 7.9 +/- 4.9
         南10.0 6.8 +/- 5.6
                       12.0 7.3 +/- 5.2
                       15.0 8.7 +/- 6.0
名称：实际，dtype：对象 

平均等待时间，可能是一分钟或两分钟，是计划间隔的一半以上，但不等于计划间隔，正如等待时间悖论所暗示的那样。 换句话说，确认了检查悖论，但是等待时间悖论不成立。

结论

潜伏期悖论是包括建模，概率论以及将统计假设与现实进行比较的讨论的有趣起点。 尽管我们已经确认在现实世界中，公交路线遵循某种检查悖论，但以上分析却非常令人信服：等待时间悖论的主要假设-公交车的到来遵循泊松过程的统计数据-是不合理的。

回想起来，这并不奇怪：泊松过程是一种无记忆的过程，它假设到达的概率完全独立于自上一次到达以来的时间。 实际上，一个管理良好的公共交通系统具有专门安排的时间表来避免这种情况：公交车在白天不会随机发车，而是根据为提高乘客运输效率而选择的时间表发车。

更为重要的一课是要谨慎对待任何数据分析任务的假设。 有时，泊松过程可以很好地描述到达时间数据。 但是，仅仅因为一种数据类型听起来像另一种数据类型，并不意味着一种允许的假设对于另一种肯定是有效的。 似乎正确的假设通常会得出不正确的结论。