一年半以前,我发表了文章
“手指上的数学:最小二乘法” ,该文章收到了非常不错的答复,其中包括我提议画一只猫头鹰的事实。 好吧,既然是猫头鹰,那么您需要再次解释它。 一周之内,我将就地质问题准确地开始一些演讲; 我借此机会,在这里提出(适应的)要点作为草案。 我的主要目标不是从一本关于美味和健康食品的书中给出现成的食谱,而是要解释为什么这样做以及相应部分中的其他内容,因为数学不同部分之间的联系最为有趣!
目前,我打算将案文如下:
通过最大似然原理,我将侧向最小二乘,并在概率论中要求最小方向。 本文是针对我们地质学院三年级的课程而设计的,这意味着(从所涉及的设备的角度来看!)有兴趣的高中生应该以适当的热情来理解它。
定理的声音是多少,或者您相信进化论吗?
有一天,有人问我是否相信进化论。 现在暂停一下,想想您将如何回答。

就我个人而言,我感到吃惊,并回答说我认为它是可信的,而信仰的问题根本不在这里出现。 科学理论与信仰无关。 简而言之,该理论仅建立了我们周围世界的模型,没有必要相信它。 而且,
波普尔的标准要求科学的理论能够反驳。 合理的理论首先还应具有预测能力。 例如,如果您以某种方式对农作物进行基因改造,使其本身产生农药,那么逻辑上就会出现对农作物具有抗性的昆虫。 但是,通过将普通植物与转基因植物并排生长可以减慢这一过程的可能性明显不足。 根据演化理论,相应的模拟做出了
这样的预测 ,并且似乎得到了
证实 。
最小平方与它有什么关系?
如前所述,我将通过最大似然原理去最小二乘。 让我们用一个例子来说明。 假设我们对企鹅的生长数据感兴趣,但是我们只能测量其中一些美丽的鸟类。 将增长分配模型引入任务中是很合逻辑的-通常,这是正常现象。 正态分布的特征在于两个参数-平均值和标准偏差。 对于参数的每个固定值,我们可以计算出将准确生成我们进行的那些测量的概率。 此外,通过改变参数,我们找到了使概率最大化的参数。
因此,为了最大可能地工作,我们需要根据概率论进行操作。 稍微降低一点,我们定义了概率和可能性的概念,但首先,我想着重于另一个方面。 令人惊讶的是,我很少看到人们想到“概率论”一词中的“理论”一词。
什么是学习定理?
关于概率估计的起源,含义和范围,暴力辩论已经进行了一百多年。 例如,
布鲁诺·德·芬内蒂 (
Bruno De Finetti)指出,概率不过是对某种事物将要发生的概率的主观分析,而这种概率并不存在于心灵之外。 这是一个人愿意对发生的事情进行押注。 这种观点与
经典/格言主义者关于某个事件的特定结果的概率的观点完全相反,在该观点中,假定同一事件可以重复多次,并且特定结果的“概率”与特定结果在重复测试中掉落的频率有关。 除了主观主义者和客观主义者,还有一些客观主义者认为,概率是宇宙的真实方面,而不仅仅是对观察者信心程度的描述。
尽管可能如此,但是实践中所有三所科学学校都使用基于科摩莫罗夫公理的同一仪器。 让我们从主观主义的观点出发,以建立在柯尔莫哥罗夫公理基础上的概率论为基础,提出间接论证。 我们稍后再给出公理,但是首先,我们假设我们有一家博彩公司,可以接受下一届世界杯的赌注。 让我们进行两个事件:a =乌拉圭队将成为冠军,b =德国队将成为冠军。 庄家估计乌拉圭队获胜的机会为40%,德国队获胜的机会为30%。 显然,德国和乌拉圭不能同时获胜,因此a∧b的机会为零。 好吧,同时,庄家相信乌拉圭或德国(而不是阿根廷或澳大利亚)获胜的概率为80%。 让我们以以下形式编写它:

如果庄家声称自己对事件
a的置信度为0.4,即
P(a) = 0.4,则玩家可以选择是否下注
a来下注与庄家的置信度相称的金额。 这意味着玩家可以通过在庄家的六卢布下注四卢布来押注事件将发生。 或者玩家可以下注六卢布,而不是博彩公司的四卢布,这将不会发生。
如果博彩公司的信心度不能准确反映世界状况,那么我们可以指望这样的事实,从长远来看,它将使那些信念更加准确的玩家蒙受损失。 此外,在该特定示例中,玩家具有庄家
总是赔钱的策略。 让我们来说明一下:

玩家下了三个赌注,无论冠军的结果如何,他总是赢。 请注意,原则上考虑的奖金不包括乌拉圭或德国是冠军的最爱,因此保证了庄家的损失! 这种情况是由以下事实导致的:博彩公司没有遵循概率论的基本原则,因为它违反了Kolmogorov的第三个公理,让我们把这三个都带给他们:
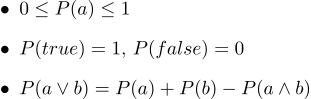
在文本形式中,它们如下所示:
- 1.所有概率范围从0到1
- 2.当然,正确的陈述的概率为1,当然错误的概率为0。
- 3.第三个公理是析取公理,很容易直观地理解,注意到那些陈述a为真的情况以及b为真的情况肯定涵盖了a∨b陈述为真的所有情况; 但在两组情况的总和中,它们的相交发生两次,因此有必要减去P(a∧b)。
1931年,de Finetti提出
了非常有力的声明:
如果庄家受到许多置信度的指导,这违反了概率论的公理,那么玩家下注的这种组合可以确保每次下注都输掉庄家(玩家获胜)。
概率公理可以被认为是限制某些行为者可以持有的概率性信念的集合。 请注意,跟随庄家并不意味着科尔摩哥罗夫将赢得胜利的公理(我们将把佣金问题放在一边),但是如果您不遵循这些规则,则一定会保证他会输。 注意,还提出了其他论据来支持应用概率; 但是正是基于概率论的推理系统在
实践中的成功,才被证明是一种诱人的诱因,引起了许多观点的修正。
因此,我们稍微揭开了Theorver
为何有意义的面纱,但是它操纵哪种对象? 整个理论仅基于三个公理。 这三个都包含一些魔术函数
P。 而且,看这些公理,它使我非常想起形状区域功能。 让我们尝试看看该区域是否可以确定概率。
我们将“事件”一词定义为“单位正方形的子集”。 我们将“事件的概率”一词定义为“相应子集的区域”。 粗略地说,我们有一个很大的硬纸板目标,我们闭上眼睛向它射击。 子弹落入给定组的机会与该组的面积成正比。 在这种情况下,可靠的事件是整个正方形,例如正方形的任何点显然是错误的。 根据我们对概率的定义,不可能完美地达到目的(我们的要点是实质性要点)。 我真的很喜欢图片,而且我画了很多,因此也不例外! 让我们说明所有三个公理:
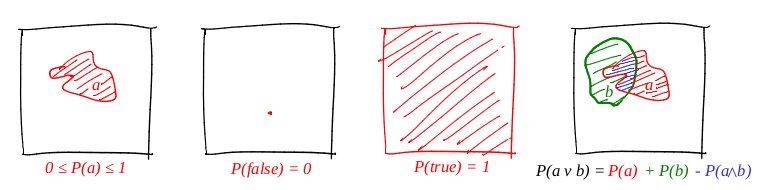
因此,满足了第一个公理:面积是非负的,并且不能超过单位。 可靠的事件是整个正方形,故意的错误事件是任何零区域集。 它与分离符完美配合!
示例的最大信誉
示例一:硬币翻转
让我们看一个简单的抛硬币的例子,又
名伯努利计划 。 进行了
N次实验,其中每一个都可能发生两个事件(“成功”或“失败”)之一,一个事件的概率为
p ,第二个事件的概率为
1-p 。 我们的任务是找到在这
n个实验中准确获得
k次成功的概率。 这个概率给了我们伯努利公式:
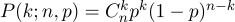
取一枚普通硬币(
p = 0.5 ),将其扔十次(
n = 10 ),并考虑将尾巴掉落多少次:
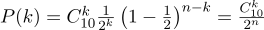
这是概率密度图:
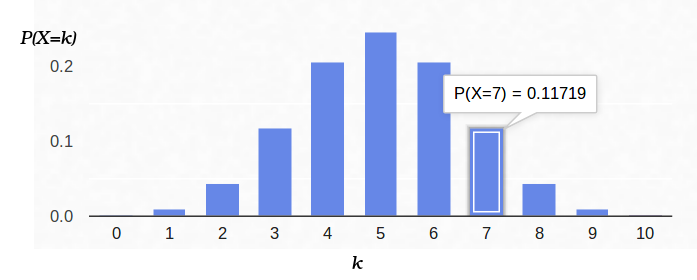
因此,如果我们固定“成功”发生的可能性(0.5),并记录实验次数(10),则“成功”的可能数目可以是0到10之间的任何整数,但是,这些结果的可能性不大。 显而易见,获得五个“成功”的可能性要比没有一个成功的可能性高得多。 例如,计数7条尾巴的概率约为12%。
现在,让我们从另一端来看同样的任务。 我们有一个真实的硬币,但是我们不知道它的先验概率“成功” /“失败”的分布。 但是,我们可以将其抛出十次并计算“成功”的次数。 例如,我们有七个尾巴。 这如何帮助我们评估
p ?
我们可以尝试将Bernoulli公式中的
n = 10和
k = 7固定,使
p为自由参数:

然后,伯努利公式可以解释为估计参数的
可能性 (在这种情况下为
p )。 我什至更改了该函数的字母,现在是
L (来自英语风格)。 也就是说,似然度是针对给定参数值生成观察数据(10个实验中有7个尾数)的概率。
例如,假设发生十次投掷中的七个尾巴,则出现平衡硬币的可能性(
p = 0.5)约为12%。 您可以绘制函数
L :
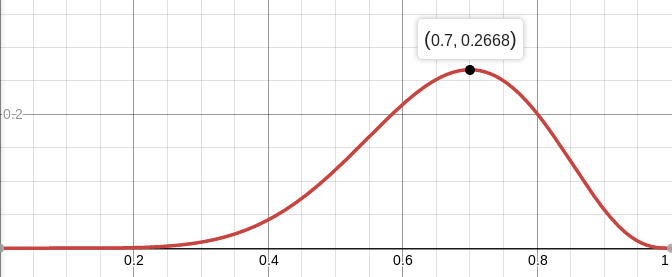
因此,我们正在寻找一个参数值,以最大程度地获得获得的观测值。 在这种特殊情况下,我们具有一个变量的功能,我们正在寻找其最大值。 为了使搜索更容易,我将查找最大值不是
L ,而是
logL。 对数是严格单调的函数,因此最大化一个和另一个完全相同。 对数将乘积分解为更易于区分的数量。 因此,我们正在寻找此功能的最大值:

为此,我们将其导数等于零:
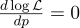
log x = 1 / x的导数,我们得到:

也就是说,达到最大可能性(大约27%)

以防万一,我们计算二阶导数:
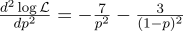
在p = 0.7处为负,因此该点实际上是函数L的最大值。
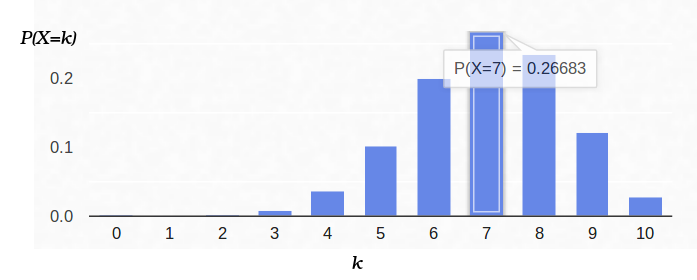
这是伯努利方案的概率密度,其中
p = 0.7:
示例二:ADC
假设我们要测量某个恒定的物理量,无论是用尺子测量长度还是用电压表测量电压。 任何测量都将给出此数量的
近似值 ,而不是数量本身。 我在此描述的方法是高斯在18世纪末提出的,当时他测量了天体的轨道。
例如,如果我们对电池电压进行N次测量,则会得到N次不同的测量结果。 选哪一个? 仅此而已! 因此,让我们有N个数量Uj:
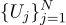
假设每个测量值Uj等于一个理想值,再加上一个高斯噪声,该噪声的特征在于两个参数-高斯钟形的位置及其“宽度”。 这是概率密度:
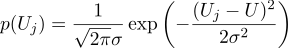
也就是说,在有N个给定的Uj值的情况下,我们的任务是找到一个使似然值最大化的参数U。 可信度(我立即从中取对数)可以写成如下形式:
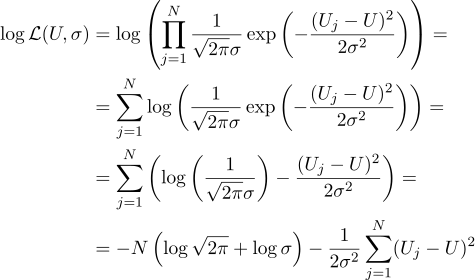
好吧,那么所有事情都和以前一样严格,对于要寻找的参数,我们等于零偏导数:
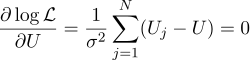
我们发现,未知量U的最可能估计值可以作为所有度量的平均值:
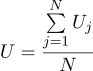
好吧,最可能的sigma参数是通常的标准偏差:
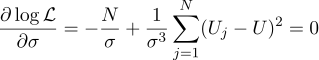

在答案中获得所有测量值的简单平均值是否值得打扰? 就我的口味而言,这是值得的。 顺便说一句,对一个恒定值的多次测量取平均值以提高测量的准确性是一种标准做法。 例如,
ADC平均 。 顺便说一句,由于该高斯噪声不是必需的,因此使噪声无偏就足够了。
示例三,再一维
我们继续进行对话,让我们以相同的示例为例,但要使其复杂一些。 我们要测量某个电阻的电阻。 在实验室电源的帮助下,我们能够通过一些标准数量的安培,并测量为此所需的电压。 也就是说,在电阻评估器的输入处将有N对数字(Ij,Uj)。
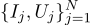
在图表上绘制这些点; 欧姆定律告诉我们,我们正在寻找蓝线的斜率。
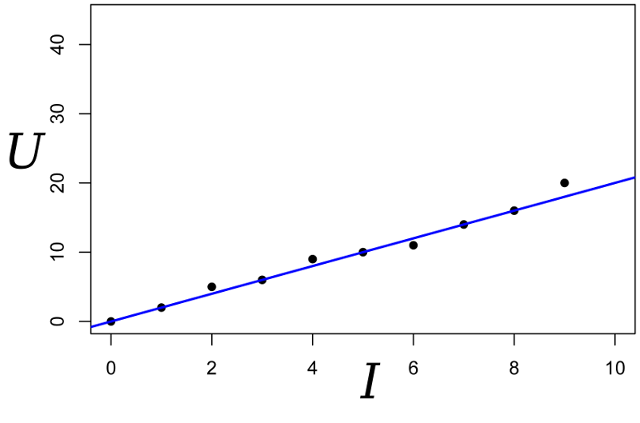
我们为参数R的可能性写表达式:
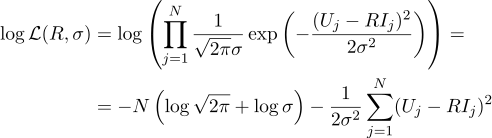
再一次,我们等于相应的偏导数为零:
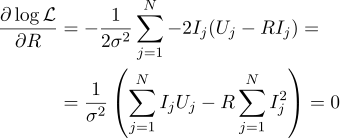
然后,可以通过以下公式找到最合理的电阻R:
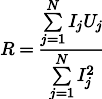
与所有测量的简单平均值相比,该结果已经不太明显。 请注意,如果我们在1安培的范围内进行100次测量,而在千安培的范围内进行1次测量,那么之前的100次测量实际上将不会影响结果。 让我们记住这一事实,在下一篇文章中对我们有用。
第四个示例:回到最小二乘
当然,您已经注意到在最后两个示例中,最大化似然对数等效于最小化估计误差的平方和。 让我们看另一个例子。 使用参考砝码对杆秤进行校准。 假设我们有N个参考载荷xj,将它们悬挂在杆秤上并测量弹簧的长度,我们得到N个弹簧长度yj:

胡克定律告诉我们,弹簧的伸展线性地取决于所施加的力,该力包括货物的重量和弹簧本身的重量。 假设弹簧刚度为参数
a ,但自重下的弹簧张力为b参数。 然后,我们可以用这种方式写出我们的测量可能性的表达式(像以前一样,在高斯测量噪声的假设下):
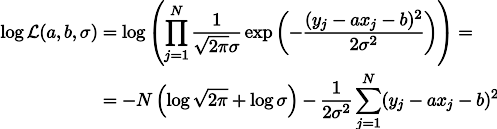
L的可能性的最大值等效于最小化估计误差的平方和,也就是说,我们可以搜索如下定义的函数S的最小值:
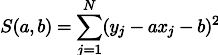
换句话说,我们正在寻找一条使绿色段长度的平方和最小的直线:
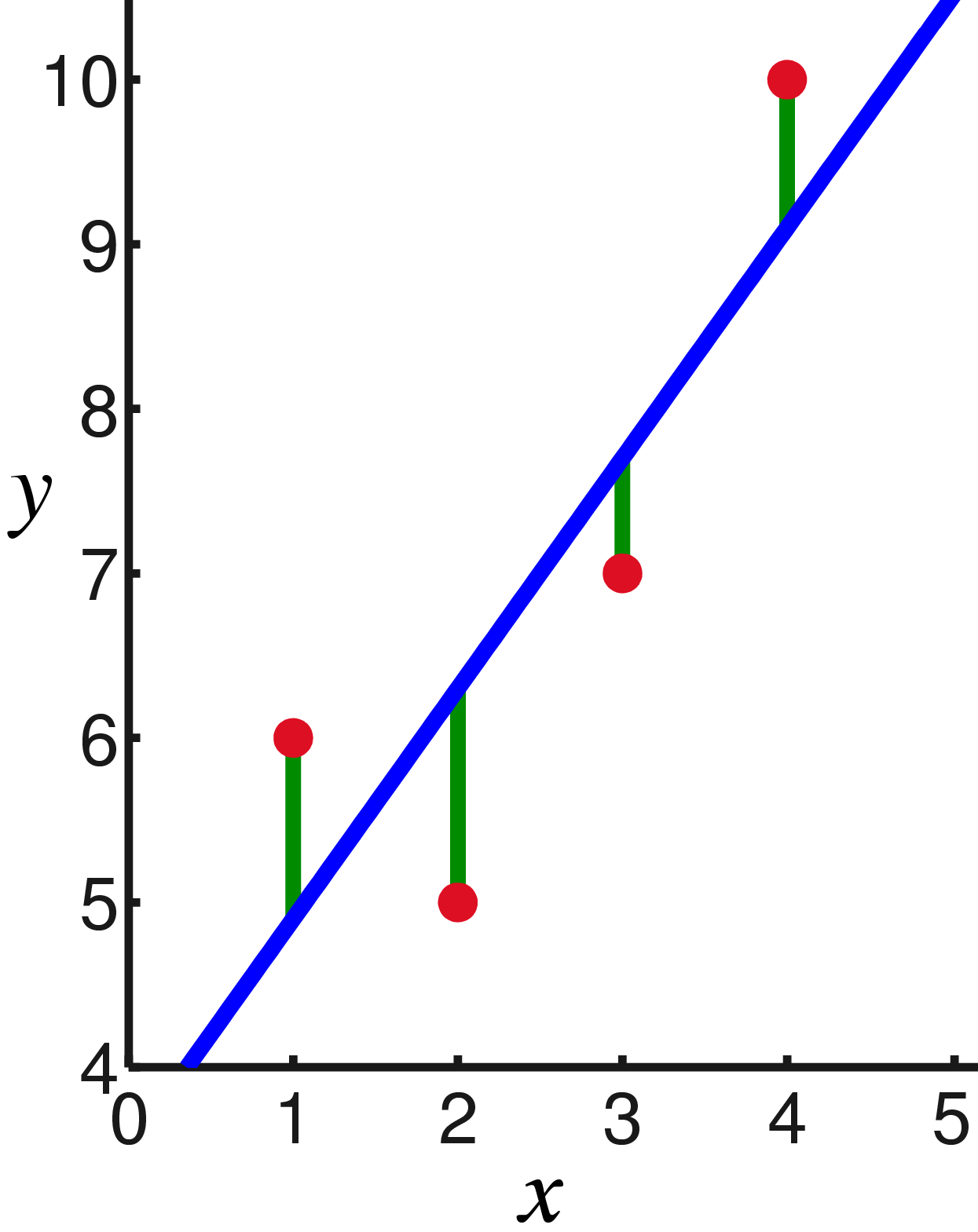
好吧,那就不足为奇了,我们将偏导数设置为零:
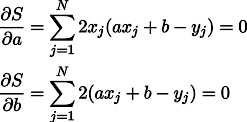
我们得到了两个线性方程组,其中有两个未知数:
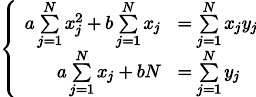
我们回想起学校的七年级,并写出解决方案:

结论
对于那些概率密度为高斯的情况,最小二乘法是使可能性最大化的一种特殊情况。 在密度(根本不是高斯)的情况下,最小二乘法给出的估计与MLE不同(最大似然估计)。 顺便说一下,高斯曾一次假设分布不起作用,只有测试的独立性很重要。
从本文中可以看到,深入森林越深,对这个问题的分析解决方案就越麻烦。 好吧,是的,我们不是在18世纪,而是拥有计算机! 下次我们将看到针对OLS问题的几何方法以及编程方法,请继续关注。