我准备了很长时间,收集了资料,希望这次结果会更好。 我将本文专门介绍用于解决具有局限性的数学优化问题的基本方法,因此,如果您听说单纯形法是一些
非常重要的方法,但是仍然不知道它的作用,那么本文可能会对您有所帮助。
PS本文包含由宏编辑器添加的数学公式。 他们说有时不显示。 还有许多gif格式的动画。
前言
数学优化问题是“在集合中查找”形式的问题
\数学K 元素
x∗ 这样对于所有人
x 来自
\数学K 已执行
f(x∗) leqf(x) “,这在科学文献中很可能是这样写的
beginarrayrl mboxminimize&f(x) mboxproveded&x in mathcalK。 endarray
从历史上看,诸如梯度下降或牛顿法之类的流行方法仅在线性空间中起作用(例如,最好是简单的空间)
mathbbRn ) 在实践中,经常会遇到需要在线性空间以外的地方找到最小值的问题。 例如,您需要在此类向量上找到某些函数的最小值
x=(x1, ldots,xn) 为此
xi geq0 ,这可能是由于以下事实
xi 表示任何对象的长度。 或者例如,如果
x 表示一个点的坐标不应超过
来自
y 即
|x−y | leqr 。 对于此类问题,梯度下降或牛顿法不再直接适用。 事实证明,很多种优化问题都可以通过“限制”轻松覆盖,类似于我上面描述的那些。 换句话说,代表集合很方便
\数学K 以平等和不平等制度的形式
beginarraylgi(x) leq0,〜1 leqi leqm,hi(x)=0,〜1 leqi leqk。 endarray
形式空间上的最小化问题
mathbbRn 因此,他们开始任意地称它们为“无约束的问题”,而由平等和不平等的集合定义的集合之上的问题-“受约束的问题”。
从技术上讲,绝对有很多
\数学K 可以使用
指标 -function表示为单个等式或不等式,其定义为
I mathcalK(x)=\开始cases0,&x notin mathcalK1,&x in mathcalK, endcases
但是,这样的函数没有各种有用的属性(凸性,微分性等)。 但是,人们经常可以想象
\数学K 以几个平等和不平等的形式存在,每个都有这样的性质。 案例总结下的基本理论
beginarrayrl mboxminimize&f(x) mbox提供&gi(x) leq0,〜1 leqi leqm&Ax=b, endarray
在哪里
f,gi -凸(但不一定可微)函数,
-矩阵。 为了演示这些方法的工作原理,我将使用两个示例:
- 线性编程任务
$$显示$$ \开始{array} {rl} \ mbox {minimize}&-2&x ~~~-&y \\ \ mbox {提供}&-1.0&〜x -0.1&〜y \ leq -1.0 \ \&-1.0&〜x +〜0.6&〜y \ leq -1.0 \\&-0.2&〜x +〜1.5&〜y \ leq -0.2 \\&〜0.7&〜x +〜0.7&〜y \ leq 0.7 \\&〜2.0&〜x -0.2&〜y \ leq 2.0 \\&〜0.5&〜x -1.0&〜y \ leq 0.5 \\&-1.0&〜x -1.5&〜y \ leq- 1.0 \\ \ end {array} $$显示$$
本质上,此问题在于找到方向(2,1)上多边形的最远点,问题的解决方案是点(4.7,3.5)-多边形中最“右”的点。 但是多边形本身
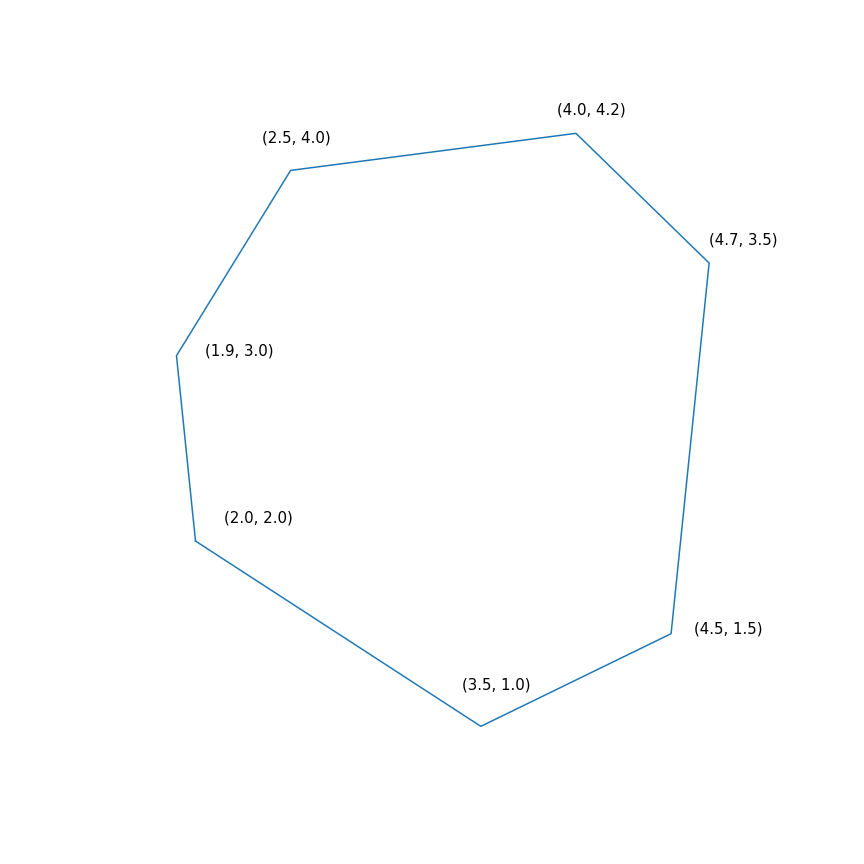
- 具有一个二次约束的二次函数的最小化
beginarrayrl mboxminimize&0.7(x−y)2+0.1(x+y)2 mboxprovided&(x−4)2+(y−6)2 leq9 endarray
单纯形法
在本篇综述中介绍的所有方法中,单纯形方法可能是最著名的。 该方法是专门为线性编程开发的,提出的方法中只有一个可以在有限的步骤中实现精确的解决方案(前提是要使用精确的算术进行计算,实际上通常不是这种情况,但理论上是可行的)。 单纯形方法的思想包括两部分:
- 线性不等式和等式的系统定义了多维凸多面体(多面体)。 在一维情况下,这是点,射线或线段;在二维情况下,这是凸多边形;在三维情况下,这是凸多面体。 最小化线性函数实际上是在某个方向上找到“最远”的点。 我认为直觉应该建议这个最远的点应该是某个峰值,的确如此。 通常,对于来自 m 中的不平等 n 顶点的三维空间是满足系统的点 n 这些不平等变成平等(前提是不平等之间没有对等)。 尽管可以有很多这样的点,但总有数量有限。
- 现在我们有了一个有限的点集,通常来说,您可以简单地将它们挑选出来并进行排序,即执行以下操作:对于 n 不等式,求解根据所选不等式编译的线性方程组,验证解是否适合原始不等式系统,并与其他此类不等式进行比较。 这是一种相当简单的低效但可行的方法。 单纯形方法(而不是迭代方法)沿着边缘从上到下移动,从而提高了目标函数的值。 事实证明,如果顶点不包含函数值更好的“邻居”,那么它是最佳的。
单纯形法是迭代的,也就是说,它顺序地稍微改善了解决方案。 对于此类方法,您需要从某个地方开始,一般情况下,这是通过解决辅助问题来完成的
\开始arrayrl mboxminimize&s mbox提供&gi(x) leqs,〜1 leqi leqm endarray
如果解决这个问题
x∗,s∗ 这样
s∗ leq0 然后执行
gi(x∗) leqs leq0 否则,原始问题通常在空集上给出。 要解决辅助问题,也可以使用单纯形法,但是可以采用起点
s= maxigi(x) 随心所欲
x 。 找到起点可以任意地称为方法的第一阶段,找到原始问题的解决方案可以任意地称为方法的第二阶段。
两阶段单纯形法的轨迹使用scipy.optimize.linprog生成了轨迹。
投影梯度下降
关于梯度下降,我最近写了另
一篇文章 ,其中我也简要介绍了该方法。 现在,这种方法非常活跃,但正在作为更普遍的
近端梯度下降的一部分进行研究。 该方法的基本思想是平庸的:如果将梯度下降应用于凸函数
f ,然后通过正确选择参数,我们获得了全局最小值
f 。 如果在梯度下降的每个步骤之后校正了获得的点,而是将其投影投影到封闭凸集上
\数学K ,因此我们得到了函数的最小值
f 在
\数学K 。 好吧,或更正式地说,投影梯度下降是一种依次计算的算法
\开始casesxk+1=yk− alphak nablaf(yk)yk+1=P mathcalK(xk+1),\结束cases
在哪里
P mathcalK(x)= mboxargminy in mathcalK |x−y |。
最后一个等式定义了投影到集合上的标准运算符,实际上,根据点,它是一个函数
x 计算最接近集合的点
\数学K 。 距离的作用在这里
| ldots | ,值得注意的是,此处可以使用任何
规范 ,但是,不同规范的投影可能会有所不同!
实际上,仅在特殊情况下才使用投影梯度下降。 其主要问题是,投影的计算可能比原始投影更加困难,并且需要多次计算。 使用投影梯度下降法最方便的最常见情况是“盒子限制”,其形式为
elli leqxi leqri, 1 leqi leqn。
在这种情况下,投影的计算非常简单,结果是每个坐标
[P mathcalK(x)]i=\开始casesri,&xi>ri elli,&xi< ellixi,&xi in[ elli,ri]。 endcases
对于线性规划问题,使用投影梯度下降法完全没有意义,但是,如果您这样做,它将看起来像这样
这是第二个问题的投影梯度下降的轨迹,如果
如果
椭球法
该方法值得注意,因为它是解决线性规划问题的第一个多项式算法;可以将其视为
二分法的多维概括。 我将从
分离超平面的更通用
方法开始:
- 在方法的每个步骤中,都有一些包含问题解决方案的集合。
- 在每个步骤中,都将构造一个超平面,然后将位于选定超平面一侧的所有点从集合中移除,然后可以将一些新点添加到该集合中。
对于优化问题,“分离超平面”的构造基于凸函数的以下不等式
f(y) geqf(x)+ nablaf(x)T(y−x)。
如果修复
x ,那么对于凸函数
f 半空间
nablaf(x)T(y−x) geq0 仅包含值不小于某点的点
x ,这意味着可以将其删除,因为这些要点并不比我们已经发现的要好。 对于存在限制的问题,您可以类似地摆脱保证违反其中一项限制的要点。
分离超平面方法的最简单版本是在不添加任何点的情况下简单地切除半空间。 结果,在每一步我们都会有一个特定的多面体。 该方法的问题在于多面体的面数可能会随着步骤的增加而增加。 而且,它可以成倍增长。
椭球方法实际上在每个步骤中都存储一个椭球。 更准确地说,在构造超平面之后,将构造一个最小体积的椭球,其中包含原始零件的一部分。 这可以通过添加新点来实现。 椭球总是可以由正定矩阵和向量(椭球的中心)定义,如下所示
\ mathcal {E}(P,x)= \ {z〜|〜(z-x)^ TP(z-x)\ leq 1 \}。
包含半空间和另一个椭圆体的交点的最小椭圆体的构造可以使用
适度繁琐的公式来完成。 不幸的是,实际上,该方法仍然与单纯形方法或内点方法一样好。
但实际上它是如何工作的
和为
内点法
这种方法的发展历史悠久,最早的先决条件之一是在单纯形方法开发的同时出现。 但是当时它仍然不够有效,无法在实践中使用。 1984年晚些时候,专门为线性编程开发
了该方法的一种
变体,在理论上和实践上都很好。 而且,与单纯形法不同,内点法不仅限于线性规划,现在它是有约束的凸优化问题的主要算法。
该方法的基本思想是用所谓的
势垒函数形式的罚款代替限制。 功能介绍
F:Int mathcalK rightarrow mathbbR 称为集合的
障碍函数 \数学K 如果
F(x) rightarrow+ infty〜 mboxatx rightarrow\部分 mathcalK。
在这里
整数\数学K -里面
\数学K ,
\部分\数学K -边框
\数学K 。 代替原来的问题,提出解决问题
mbox最小化x varphi(x,t)=tf(x)+F(x)。
F 和
varphi 仅在内部给出
\数学K (实际上,这是名称的来源),屏障的属性可确保
varphi 至少
x 存在。 而且,更多
t 影响越大
f 。 在合理合理的条件下,您可以实现目标
t 到无穷远然后最小
varphi 将收敛到原始问题的解决方案。
如果设置
\数学K 作为一组不等式给出
gi(x) leq0,〜1 leqi leqm 那么障碍函数的标准选择是对
数障碍F(x)=− summi=1 ln(−gi(x))。
最低分
x∗(t) 功能
varphi(x,t) 对于不同
t 形成一条曲线,通常称为
中心路径 ,实际上,内点方法正尝试遵循此路径。 这就是它的外观
线性编程实例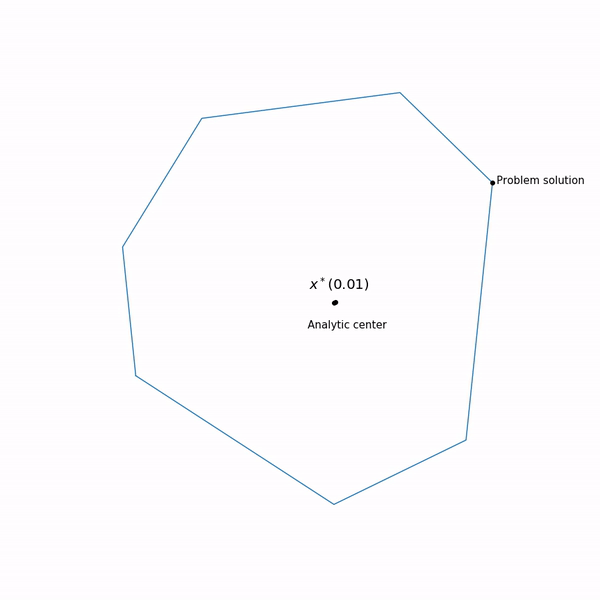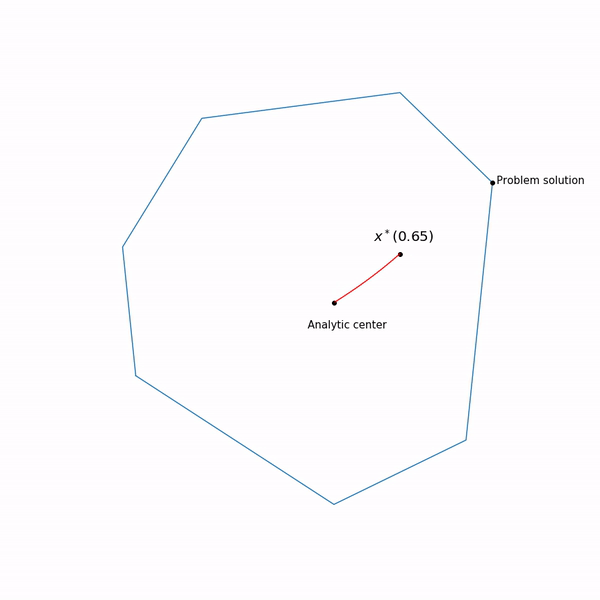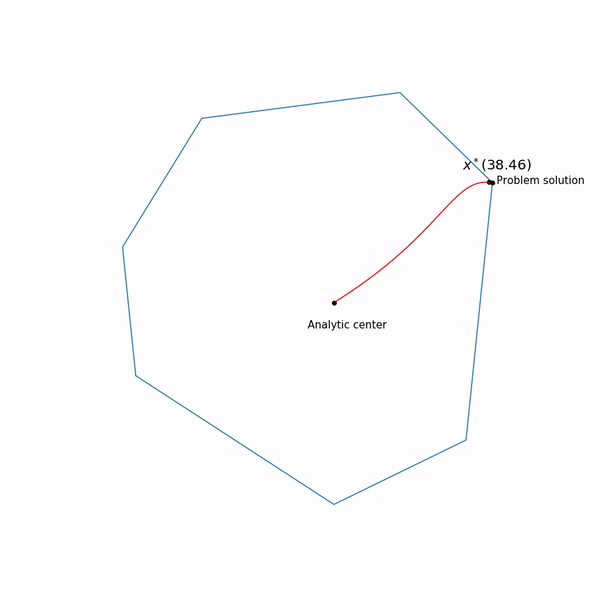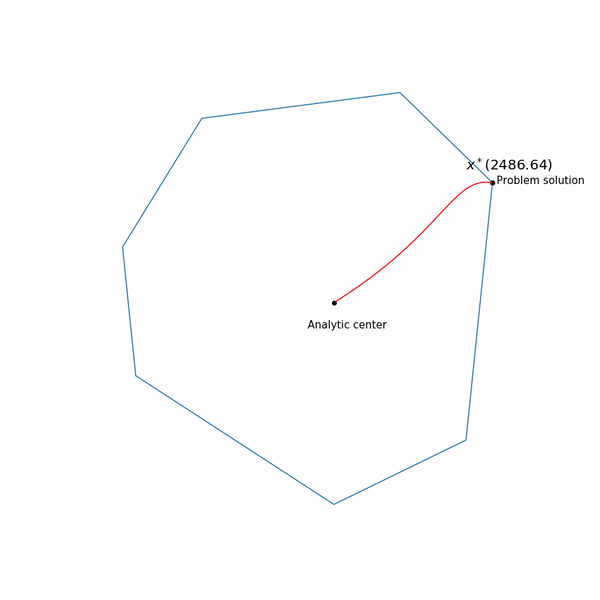 分析中心
分析中心只是
x∗(0) 最后,内部点方法本身具有以下形式
- 选择一个初始近似值 x0 , t0>0
- 使用牛顿法选择一个新的近似值
xk+1=xk−[ nabla2x varphi(xk,tk)]−1 nablax varphi(xk,tk)
- 点击放大 t
tk+1= alphatk, alpha>1
牛顿法的使用在这里非常重要:事实是,在正确选择障碍函数的情况下,牛顿法的步骤会产生一个点
,该点
保留在我们实验
的集合内 ,我们并不总是以这种形式给出。 最后,这就是内点法的轨迹
线性编程任务弹跳的黑点是
x∗(tk) ,即 这是我们在当前步骤中尝试采用牛顿法的步骤。