Geekly articles weekly

移动Yandex。Blitz：我们分析任务

在2018年，我们举办了三场Yandex.Blitz竞赛-机器学习，移动开发和前端竞赛。 最近举行了第三届比赛-恭喜获胜者！ 同时，我们想回到第二部分，在Android / iOS的算法和编写软件的交界处提出了任务。 在Yandex中担任移动开发人员职位的候选人将受益于解决此类问题的经验。 阅读其中一些的详细分析。 而且，如果您没有参加闪电战，那么最好先尝试自己解决问题 。





“供气”任务


进入结论时间限制内存限制
标准输入或input.txt标准输出或output.txt15秒15兆字节

Nika正在为一家大型天然气公司的高层管理人员开发一个应用程序，以帮助他们计划生产。


该公司正在考虑距离管道d 1 ... d i ... d n公里的n个气田，可以生产v 1 ... v i ... v n天然气单位。 每个现场出售一个单独的许可证-许可证为s 1 ... s i ... s n 。


要将田野与公路连接起来，您需要建立管道。 可以铺设不同类型管道的承包商可以帮助该公司。 管道的长度（l 1 ... l i ... l m ）和价格（p 1 ... p i ... p m ）互不相同。 它们可以根据需要相互组合。


该公司有k个硬币，并希望获得尽可能多的汽油。


如果向承包商提供最佳订单，公司将能够生产多少？


管道可能比从现场到管道的距离更长。


输入格式


第一行包含一个整数k≤10 5 。


第二行包含一个n≤15的整数。


接下来的n行包含三个整数d i≤100，v i≤100和s i≤100。


这些数字用空格分隔。


下一行包含一个m≤15的整数。


接下来的m行包含两个整数l i≤100和p i≤100。数字之间用空格分隔。


输出格式


唯一的答案。


例子


进入结论
  116
 3
 58 7 50
 81 71 56
 52 57 31
 3
 47 9
 1 25
 18 61 
  57

解析中


首先，让我们定义符号。 设一类带有参数的对象存放（deposit） $ inline $ Dd_ {i} $ inline $ （远程） $ inline $ Dv_ {i} $ inline $ （产量）和 $ inline $ Ds_ {i} $ inline $ （许可费用）。 这种类型的索引对象将是变量i。 还有一个带有参数的Pipeliner对象类 $内联$ PPl_ {j} $内联$ （承包商可以建造的管道的长度）和 $内联$ PPp_ {j} $内联$ （此管道的价格），通过j进行索引。 闪电战的参与者多次询问一种管道是否可以使用两次。 假定否，此示例将清楚显示。 因此，按照此任务的条款， $ inline $ D_ {i} = {0，1} $ inline $ （是否选择一个字段）和 $内联$ PP_ {j} = {0，1} $内联$ （是否选择承包商），您可以执行线性编程任务：


$ inline $ \ sum \ limit_ {i} D_ {i} * Dv_ {i} \ rightarrow max \\ \ sum \ limits_ {i} D_ {i} * Ds_ {i} + \ sum \ limits_ {j} PP_ { j} * PPp_ {j} \ leq k \\ \ sum \ limits {{i} D_ {i} * Dd_ {i} \ leq \ sum \ limits {{} PP_ {j} * PPl_ {j} \\ D_ { i} = {0，1}，PP_ {j} = {0，1} $内联$


例如，可以通过单纯形法解决。 但是，根据任务条款，我们只需要返回最大产量（即目标函数的值），而无需指出应该选择哪个字段和哪个承包商。 连同条件的限制，可以通过构造表dp [length] [money]的动态编程方法来解决问题，其中tablep是管道的长度，money是货币。 正确构造表格后，就可以在其中找到最大值，这就是答案。 任务的内存约束足以构建。



“塔与AI”的任务


进入结论时间限制内存限制
标准输入或input.txt标准输出或output.txt1秒64兆字节

Artem正在开发一款具有竞争力的手机游戏的人工智能。 游戏规则很简单。


在玩家之前，有n个塔，高度为c 1 ... c i ... c n 。 在回合时，玩家可以破坏其中一个塔，从而获得几个较小的塔。 玩家害怕在塔中感到困惑，因此他们同意一个限制：分离后，不应获得两个高度相同的塔。 例如，高度为7的塔可以分为（1、2、4），但不能分为（1、3、3）。 高度始终是整数。


失去一个没有可以摧毁的塔的人。


Artem有一个非常聪明的朋友，他发挥得淋漓尽致-Artem的人工智能正是与他战斗。 为了评估AI的工作，Artyom需要知道如果两个玩家都表现最佳，机器人是否应该获胜。 帮助他。


人总是先走。 他将玩AI k游戏。


输入格式


第一行包含一个整数<500。


随后是两行的k个块。


每个块的第一行是整数0 <n≤50。


每个块的第二行具有n个整数，0 <c i≤50。数字之间用空格分隔。


输出格式


k行，其中每行包含true或false，这取决于一个人是否赢得了游戏。


例子


进入结论
  2
 1个
 4
 2
 1 1 
 错误的
错误的

解析中


拟议的塔式游戏是两个玩家无法进行平局的公平最终游戏。


因此，特定玩家在游戏中的胜利取决于游戏的状态和两个玩家的移动顺序。 对于熟悉博弈论的读者来说，很明显，两个玩家的任何平等游戏实际上都等同于“他”游戏，这也意味着我们的游戏。


这是他-游戏的简要说明（ 链接到源-单击它可获得详细评论）：

有几堆，每堆都有几块石头。 一口气，玩家可以从任何一堆中取出任何数量不为零的石头并将其扔掉。 因此，当不再有剩余的移动时，即在移动时发生损失。 所有的堆都是空的。

因此，游戏“他”的状态由无序的自然数集唯一地描述。 一口气，可以严格减少任何数字（如果结果是零，则将其从集合中删除）。

nim游戏的解决方案是从堆的大小中找到xor总和，只有当该总和为非零时，我们才能清楚地声明我们处于获胜状态。


此外，Sprag-Grandi定理对我们有所帮助，该定理指出两个玩家的任何相等游戏的状态U都可以与少数几个X大小的他游戏相关联。一旦指定了我们游戏状态到他的映射的函数是一个游戏，该问题的解决方案就会减少。解决它—一个已知的游戏。



任务“等级指示”


进入结论时间限制内存限制
标准输入或input.txt标准输出或output.txt1秒64兆字节

Galya正在开发评论汇总器。 她决定在七角星的帮助下指定机构的等级。


输入渲染系统接收一个高度为h且宽度为w的矩形，该矩形的左上角位于点（x，y）。 必须按照以下规则绘制星星：


  1. 星星的大小取决于矩形的宽度或高度-较小。 （请参阅图纸。）
  2. 如果矩形的尺寸之一大于星形的相应尺寸，则星形应以该尺寸为中心。
  3. 星星是向上的。

渲染系统期望从Gali代码获得恒星顶点的坐标。 帮助大风计算它们。


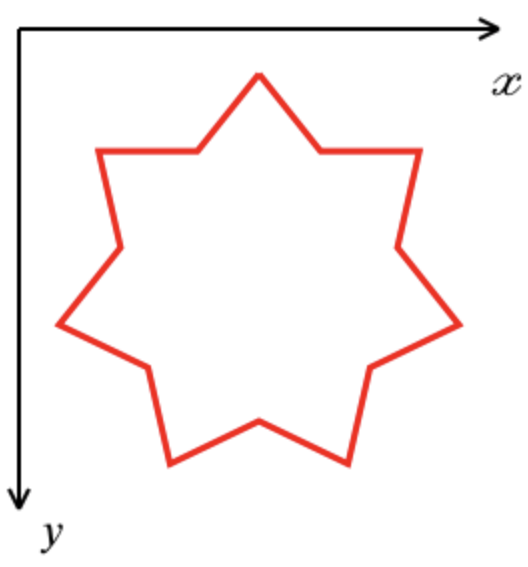
为了构建七角星，Galya采用通过将正七边形的顶点通过一个顶点连接而获得的图形外轮廓。 在坐标系中，X轴从左到右，Y轴从上到下。 Gali程序不会崩溃，接收到不正确的宽度和高度值作为输入。


输入格式


一行包含整数x，y，w和h，以空格分隔。


示例：条目150 0 50 100表示​​一个矩形，其宽度为50点，高度为100点，并且左上角为点（150，0）。


输出格式


唯一包含28个由空格分隔的数字的线是恒星顶点的坐标，从顶部开始，然后再顺时针旋转。 数字必须四舍五入到最接近的整数。 在继续解决方案之前，请参阅输出示例和问题说明。


示例：三个点（1、2），（3、4），（5、6）的输出应如下所示：1 2 3 4 5 6。


例子


进入结论
  0 0 100 100 
  50 1 65 21 90 21 85 45 100 64 78 75 72 99 50 88 28 99 22 75 0 64 15 45 10 21 35 21

注意事项


  • 要求的精度是10个有效数字。


  • 坐标系：X轴从左到右，Y轴从上到下：





  • 预期顶点顺序：



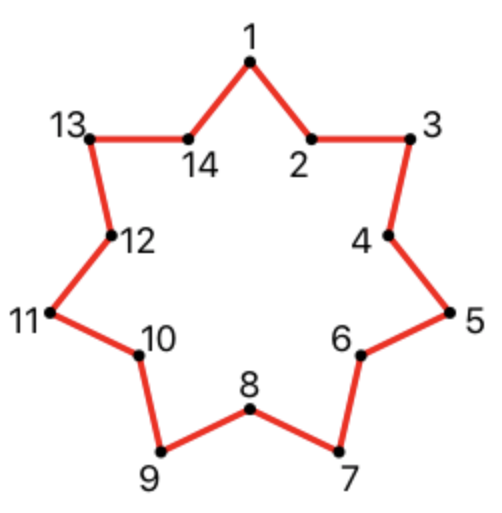
刻星的例子：




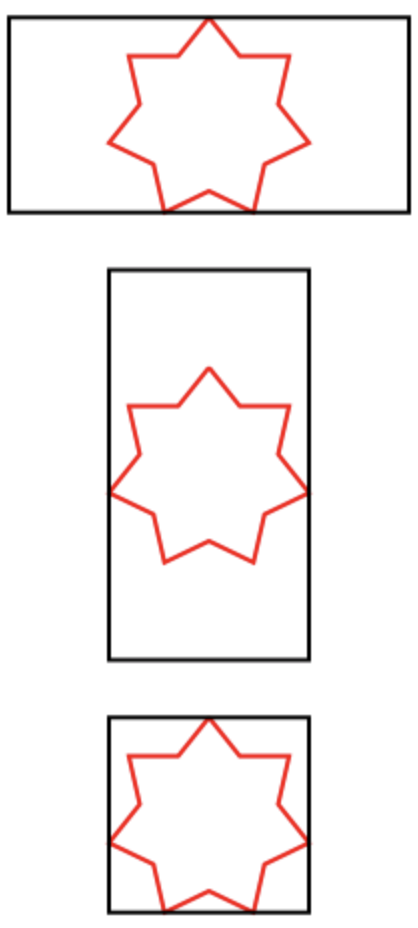
解析中


解决该问题的方法可分为三个阶段：建立具有所需空间方向的参考恒星，缩放结果点，计算并应用偏移量。


造星
最简单的方法是构建以圆弧内切的恒星，其单位半径以原点为中心。 外部顶点的点是使用平凡三角函数计算的，但内部顶点的任务则稍微复杂一些。 至少可以通过两种方式找到它们。 一种更简单的方法是找到连接外部顶点的线段的交点。 更复杂的是找到一种公式，用于根据外接圆的半径来计算外接圆的半径。 最简单的方法是，例如，对于5点星，然后将其广义化为N点星，并且在相连的顶点之间具有任意间距。


缩放比例
在所有情况下，都给出了需要适合恒星的大小。 因此，我们需要缩放获得的点，以使从最左边到最右边的距离不超过指定的宽度，并且从最高到最低的距离不超过指定的高度。 我们采用比例因子将宽度和高度设为所需的值，然后选择较小的值。 由于我们谨慎地构建了一个以原点为中心的参考星，因此只需将每个点的坐标乘以所选系数就足够了。


偏移量
剩下的最后一件事是移动我们的点，以使星星在给定的帧内。 可以将所有选项的输入数据简化为具有给定左上角坐标的边界框。 这里的一切都很简单：我们从上一阶段获得的结果中获取最高点，考虑其y坐标与左上角y坐标的差，然后将所有点垂直移动获得的值。 我们用x坐标做同样的事情，只是不取最高点，而取最左边的点。 最后一点就是：将星星居中于该矩形中。


进一步的操作取决于我们在上一阶段选择的系数：


  • 如果按比例缩放-我们将矩形的宽度与从左到最右点的距离之间的差值计算在内；
  • 如果按比例缩放-我们计算矩形的高度与从最高点到最低点的距离之间的差。

将获得的值除以2，然后根据相应的测量值移动点。 收到答复。



任务“圆的旋转和缩放”


进入结论时间限制内存限制
标准输入或input.txt标准输出或output.txt1秒64兆字节

Vika正在为智能手机和平板电脑开发图形编辑器。 她想让用户有机会用两个手指在屏幕上旋转一个圆圈并更改其大小，如下所示：




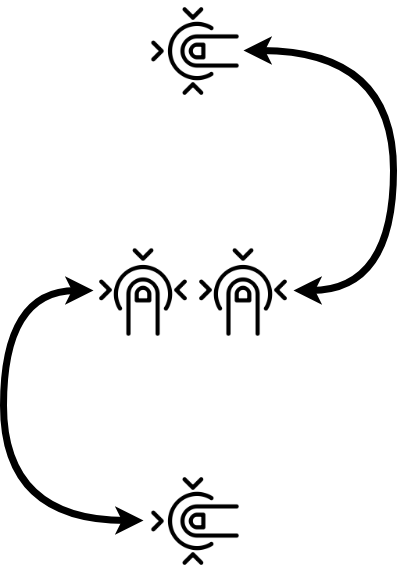
图形旋转的角度与连接手指的线段旋转的角度相同。 图形的大小与段的长度成比例地变化。 首先，旋转图形，然后更改其大小。 最初，圆具有坐标（x，y）和半径r。 给出了描述用户手势的触摸事件列表。 帮助Vika计算圆心及其半径的最终坐标。 圆相对于点（a，b）旋转。


触摸事件的描述包含手指ID，坐标和事件类型。 用户连接的第一根手指的ID为0，第二根手指的ID为1，依此类推。


一个例子：
0 337 490 ACTION_DOWN-这意味着手指（0，337，490）为0时，发生了ACTION_DOWN事件。


触摸事件具有以下类型：


  • ACTION_DOWN-用户在给定点将第一根手指应用于屏幕。
  • ACTION_POINTER_DOWN-用户在给定点将第二根手指应用于屏幕。
  • ACTION_MOVE-用户已将手指移至给定点。
  • ACTION_POINTER_UP-用户将第二根手指移至指定点并释放它。
  • ACTION_UP-用户将第一指移至指定点并释放它。
  • ACTION_CANCEL-用户中止手势。

输入格式


第一行包含数字x，y和r，以空格分隔。 第二行包含数字a和b，以空格分隔。 接下来的几行包含连续的触摸事件。


输出格式


唯一具有坐标和半径的线。 数字用空格分隔。


例子


进入结论
  25219478
 445,559
 0337490 ACTION_DOWN
 1,599,490 ACTION_POINTER_DOWN
 1,576,564 ACTION_MOVE
 1,552,590 ACTION_MOVE
 0 407,375 ACTION_MOVE
 1505615 ACTION_MOVE
 1482620 ACTION_MOVE
 0 477 360 ACTION_MOVE
 1,435,616 ACTION_MOVE
 1,411,607 ACTION_MOVE
 0547386 ACTION_MOVE
 1364548 ACTION_POINTER_UP
 0571387 ACTION_UP 
  83170473

注意事项


显示结果时，必须根据数学舍入规则将所有浮点值舍入为整数值。


解析中


尽管手势看起来很复杂，但可以将其分为两个部分：旋转和缩放。 要旋转图形，我们需要计算旋转角度，可以使用以下公式获得旋转角度：
a = atan2（prevTouchX2-prevTouchX1，prevTouchY2-prevTouchY1）-atan2（currentTouchX2-currentTouchX1，currentTouchY2-currentTouchY1）。


收到旋转角度后，您需要旋转图形本身，这减少了以旋转角度旋转图形的每个点。 旋转图形之后，我们需要对其进行缩放。 缩放数字是非常琐碎的。 收到第二根手指的ACTION_POINTER_DOWN事件时，必须记住第一根手指和第二根手指之间的距离，然后，通过跟踪前两个手指之间的距离，可以计算出缩放图形所需的系数。



任务“道路建设”


进入结论时间限制内存限制
标准输入或input.txt标准输出或output.txt1秒64兆字节

在手机游戏中，主要角色在遥远的星球上建立基础。 他从外围开始-塔由直接的激光墙连接。 总部的建筑师向他发送了一个计划，其中显示了n座坐标为（x 1 ，y 1 ）...（x i ，y i ）...（x n ，y n ）的塔。 从基础防御的角度来看，将三个或更多相邻的塔放在一条直线上是没有意义的。 但是，工作人员建筑师有时会以这种方式放置塔楼，因此玩家本人必须删除多余的中间塔楼。


完成外围任务后，英雄开始从内部装备基地。 他想在两座塔之间建造k条道路-该道路可以连接任意两座不相邻的塔，但不能越过另一条道路或墙壁。 一根塔可以走出任意多条道路。


英雄有p个道路机器人。 为了选择最佳的道路建设计划，英雄指示他们对所有可能的选项进行分类。 机器人开始同时并一遍又一遍地工作，为道路的定位带来独特的选择。 如果在下一次迭代之前发现剩余的选项比机器人少，则释放多余的机器人并将其发送到厨房做饭。 其余的机器人完成最后一个选项并关闭。


如果事实证明您可以在基地外部铺路，则英雄会宣布基地不安全并飞离地球。


厨房里可以工作多少个机器人？


输入格式


第一行包含三个整数4≤n≤10 7，1≤k≤n和质数105 <p <11×104。这些数字用空格分隔。


接下来的n行包含两个整数0 <x i ，y i <109。数字之间用空格分隔。


输出格式


唯一的答案。 如果底座不安全，则打印-1。


例子1


进入结论
  4 1 101363
 0 0
 1 0
 1 1
 0 1 
  101361

铺设唯一道路的方法有两种：（0，0）-（1，1）和（1，0）-（0，1）。 将使用两个机器人，其余的将进入厨房：p-2 = 101361。


例子2


进入结论
  4 1 101363
 1 0
 2 0
 0 1
 1 2 
  -1

在这里，您可以在（1，0）-（0，1）之间建立一条道路，该道路位于基座外部。 英雄认为基地是不安全的，答案是-1。


例子3


进入结论
  4 1 101363
 0 0 
 1 0
 2 0
 0 1 
  101363

塔（0，0），（1、0）和（2，0）在同一行上，因此英雄不会建造中间塔（1，0）。 无法铺平道路，因此，所有机器人都会立即去厨房：p = 101 363。


解析中


我们将问题的解决分为三个步骤。


第一步是确定输入顶点数据集是否多边形是凸的，如果是，则确定多边形具有多少个真实顶点。 如果多边形的所有顶点都位于支持任意边的线的一侧，则该多边形为凸形。 对于每三个相邻的顶点 $ inline $（x_ {i-1}，y_ {i-1}），（x_ {i}，y_ {i}），（x_ {i + 1}，y_ {i + 1}）$ inline $ 建立几个向量 $ inline $ ab =（（x_ {i-1}，y_ {i-1}），（x_ {i}，y_ {i}））和bc =（（x_ {i}，y_ {i}）， （x_ {i + 1}，y_ {i + 1}））$内联$ ，并计算表达式ab.x bc.y-bc.x ab.y的符号。 如果表达式为0，则顶点位于一条直线上，根据问题的情况，位于中间峰的塔楼将消失，从而减少了塔楼的总数。 如果对于所有三个顶点，乘积符号均为0或始终相同，则转到第二步；否则，我们认为基数不安全，并打印答案-1。


第二步。 构造一个凸N边形内的k个不相交对角线的方法是 $ inline $ V = 1 /（k + 1）{N-3 \选择k} {N + k-1 \选择k} $ inline $ ，但我们需要计算表达式p-V mod p，其中p是质数。


想象N！ 怎么 $内联$ a * p ^ e $内联$ ，其中最大公因数是a，且p gcd（a，p）= 1。


$ inline $ {n \ select r} =（n！）/（r！（nr）！）= a_ {1} * p ^ {e_ {1}} / a_ {2} * p ^ {e_ {2} } * a_ {3} * p ^ {e_ {3}} =（a_ {1} / a_ {2} * a_ {3}）* p ^ {e_ {1} -e_ {2} -e_ {3} } $ inline $


如果 $ inline $ e_ {1} -e_ {2} -e_ {3}> 0 $ inline $ ，则表达式可以被p整除，问题的答案是p。


对于情况 $ inline $ e_ {1} -e_ {2} -e_ {3}> 0 $ inline $ = 0，答案将是 $ inline $ a_ {1} / a_ {2} * a_ {3} $ inline $ mod p。


在计算中，我们考虑到a b mod p =（a mod p） （b mod p）mod p，并且 $ inline $ k ^ {-1} $ inline $ mod p = $ inline $（k）^ {p-2} $ inline $ mod p为质数p。


第三步。 计算表达式 $ inline $ e_ {1} -e_ {2} -e_ {3} $ inline $ 想像n！ 如1 2 ... p （p + 1） ... 2p （2p +1） ...，而（p +1） ... （2p-1）mod p = 1 2 ...（p-1 ）=（p-1）！..总计，n mod p =（ $ inline $（p-1）！^ k $ inline $ k （n mod p）！）mod p，其中k =底数（n / p）。



任务“超级简单的计划程序”


进入结论时间限制内存限制
标准输入或input.txt标准输出或output.txt10秒224兆字节

在智能手机处理器上要执行n个任务。 它们的实现需要t 1 ... t i ... t n个时间单位，并且在第i个时间单位的开始之前，第i个任务必须完成。


为了及时，可以在多个线程中执行任务，但是，每个新线程都会给电池增加负载。 在第一个流中，每单位时间消耗一个单位的能量，在第二个半单元中消耗的能量，在第三个中的能量是第二个中能量的一半，等等。


任务可以分为多个时间单位：首先，部分完成一个任务，然后继续进行另一个任务，然后返回第一个任务。 您不能同时在不同线程中执行任务的不同部分。


调度程序一次接收一个任务； 收到任务后，他立即为其分配时隙。 分配任务后，调度程序无法将其传输到其他插槽。


如果优化分配所有任务，将需要多少能量？


输入格式


第一行包含整数1 <n≤3×10 3 。
接下来的n行包含两个整数0≤t i≤10 4和0≤d i≤10 4 。 数字用空格分隔。


输出格式


唯一的答案。 准确性-八位小数。


例子


进入结论
  5
 2 2
 1 1
 3 4
 1 10
 1 2 
  10.25000000

解析中


由于根据问题的情况，仅计算消耗的能量就足够了，因此我们可以通过计算每个单位时间消耗的能量来使用求解方法。 在计划任务时，我们将消耗的能量的最小值k = 1，从任务的截止日期开始，我们对时间间隔的所有时间段进行排序。


如果时隙的能耗小于系数（k），并且在计划任务时未使用此时隙，则我们将时隙的系数增加K来占用此时隙以完成任务。当到达时间段的开始时，我们需要将系数k增加1.5倍，然后从截止日期开始重复搜索时隙，直到完成任务计划为止。完成所有任务的计划后，仅需通过添加每个时间单位的系数来计算总能耗。



可破坏对象任务


进入结论时间限制内存限制
标准输入或input.txt标准输出或output.txt2秒64兆字节

2D- . , : n- (x 1 , y 1 )...(x i , y i )...(x n , y n ). — , . . , — , .


, [0 1 2 3 4], 1 3 1 3, [1 2 3] [0 1 3 4].


, . . , , .


, ?



n ≤ 500. n x y. .



. — .


例子1


结论
  4
100 100
200 100
200 200
100 200 
 0.000000

例子2


结论
  6
167 84
421 84
283 192
433 298
164 275
320 133 
 326.986753


, , . « » : — . : , ( ) .


, ? ( , , ). : , , , . , , ( ) . even-odd rule: . — , ( ) , — .


, , — , . (, , ):


  • ( );
  • : , - ;
  • ( , 10-5 );
  • even-odd rule — ;
  • : 180 .


«DNA»


结论
input.txtoutput.txt8128

, . , , . n . , . : A, T, G C. . .



n. n . . 6⋅10 6 .



. . . . . , .



( , ):

5
TTT
GAAGCT
CAAT
AGA
AGGCA

:
2 TTT
6 AGA
28 AGA
30 AGA
57 CAAT
86 AGA
100 GAAGCT
190 TTT
191 TTT
196 AGA
219 TTT
232 AGA
271 TTT
284 TTT
285 TTT
298 TTT
320 TTT
330 TTT
331 TTT
342 TTT
373 AGA
397 AGA
488 AGA
509 AGA
524 AGA
565 TTT
574 AGA
605 AGA
625 CAAT
630 AGA
681 CAAT
718 TTT
719 TTT
744 AGGCA
754 AGA
784 AGA
808 TTT
821 CAAT
833 AGA
861 CAAT
879 AGA
921 AGA
955 AGA



, . — , — . , . . , .


, .



«QR Quest»


结论
input.txtoutput.txt164




t, . t n i , .



t , .


例子1


结论
  4
8 10 1 9 2 6 7 8
14 2 0 11 10 4 1 0
6 6 4 1 10 0 11 6
11 4 3 4 14 8 12 5 
  0
 13
 15
 5

例子2


结论
  4
9 10 6 2 12 11 7 2
3 10 1 14 13 13 1 1
6 8 8 5 3 2 6 4
5 11 5 5 3 1 10 7 
  3
 9
 2
 7


, . QR- , . - .


总共输入了8个数字-这些表中单元格的坐标，即4对与列和行的坐标。有必要猜测对这些单元格执行了哪些操作，以及从哪个表中获得了一个额外的单元格。


使用简单的操作，可以验证这是表A，B和C的四个单元格的异或总和，并通过索引a 0 ... a 7寻址：
R = A [a 0，a 1 ] ^ B [a 2，a 3 ] ^ B [a 4，a 5 ] ^ C [a 6，a 7 ]。

Source: https://habr.com/ru/post/zh-CN428882/

More articles:


All Articles