如何创建游戏AI：初学者指南

我遇到了有关游戏中人工智能的有趣材料。 通过简单的示例解释了有关AI的基本知识，并且在内部有许多有用的工具和方法可以方便地进行开发和设计。 还有如何，何时何地使用它们的信息。

大多数示例都是用伪代码编写的，因此不需要深入的编程知识。 在削减的35张带有图片和GIF的文本下面，做好准备。

UPD 很抱歉 ，但是PatientZero已经在Habré上翻译了这篇文章。 您可以在此处阅读其版本，但是由于某种原因，这篇文章使我无法通过（我使用了搜索功能，但是出了点问题）。 而且由于我正在写一个游戏开发者博客，所以我决定将我的翻译选项留给订阅者使用（某些时刻对我来说有所不同，有些是有意向开发者建议的）。

什么是AI？

游戏AI着重于根据对象所处的条件对对象执行哪些操作。 通常将其称为“智能代理”的管理，其中代理是游戏角色，车辆，机器人，有时是更抽象的东西：一整套实体，甚至是文明。 在每种情况下，它都是必须看到周围环境，在其基础上做出决定并根据其采取行动的事物。 这称为感觉/思考/行为周期：

• 感觉：代理发现或接收有关其环境中可能影响其行为的信息（附近的威胁，要收集的物品，有趣的研究场所）。
• 思考：代理决定如何反应（考虑是否可以安全地收集物品或是否必须先战斗/躲藏）。
• 行动：代理执行行动以执行先前的决定（开始向对手或对象移动）。
• ...现在情况由于字符的作用而发生了变化，因此该循环以新数据重复。

人工智能倾向于关注循环的感觉部分。 例如，自动驾驶汽车可以拍摄道路图片，并将其与雷达和激光雷达数据结合起来并进行解释。 通常，这是通过机器学习来完成的，它会处理传入的数据并赋予它们含义，并提取语义信息，例如“前方还有20码的另一辆汽车。” 这些就是所谓的分类问题。

游戏不需要复杂的系统来提取信息，因为大多数数据已经是其中不可分割的一部分。 无需运行图像识别算法来确定前方是否有敌人-游戏已经在决策过程中直接知道并传输信息。 因此，感觉循环的一部分通常比思考和行动简单得多。

游戏AI限制

AI有许多必须遵守的限制：

• AI不需要像机器学习算法那样预先训练。 在开发过程中编写神经网络来监视成千上万的玩家并学习与之对抗的最佳方法是毫无意义的。 怎么了 因为游戏尚未发布，但没有玩家。
• 游戏应具有娱乐性和挑战性，因此代理商不应找到对付人的最佳方法。
• 特工需要看起来真实，以便玩家感觉自己正在与真实的人对抗。 AlphaGo表现出色，但采取的步骤与传统的游戏理解相去甚远。 如果游戏模仿人类对手，就不会有这种感觉。 需要更改算法，以便做出合理的决定，而不是理想的决定。
• AI应该实时工作。 这意味着该算法不能长时间垄断处理器的使用以进行决策。 甚至10毫秒也太长了，因为大多数游戏只有16到33毫秒才能完成所有处理并移至图形的下一帧。
• 理想情况下，系统的至少一部分是数据驱动的，因此非编码人员可以进行更改，并且调整速度更快。

考虑涵盖整个感官/思考/行为周期的人工智能方法。

基本决策

让我们从最简单的游戏-Pong开始。 目标：移动平台（桨），使球从其弹起，而不是飞过去。 就像网球一样，如果不击球就会输。 在这里，AI的任务相对简单-决定移动平台的方向。

条件语句

对于AI而言，Pong有最明显的解决方案-始终尝试将平台放置在球下。

一个简单的算法，用伪代码编写：

游戏运行时的每一帧/更新：
如果球在桨的左侧：
左移桨
否则，如果球在桨的右边：
向右移动桨

如果平台以球的速度运动，那么这是Pong中AI的完美算法。 如果代理没有太多数据和可能采取的措施，则无需使任何事情复杂化。

这种方法是如此简单，以至于整个感觉/思考/行为周期几乎不引人注意。 但是他是：

• Sense部分位于两个if语句中。 游戏知道球的位置和平台的位置，因此AI会针对该信息进行查找。
• Think部分也有两个if语句。 它们体现了两个解决方案，在这种情况下，它们是互斥的。 结果，选择了以下三个动作之一-将平台向左移动，向右移动，或者如果平台已经正确放置，则什么也不做。
• “ Act”部分位于“向左移桨”和“向右移桨”语句中。 根据游戏的设计，他们可以立即或以一定速度移动平台。

这种方法称为反应式-有一组简单的规则（在这种情况下，如果代码中为if语句）响应世界的当前状态并采取行动。

决策树

Pong示例实际上等于正式的AI概念，即决策树。 该算法将其传递以便到达“叶子”-有关要采取何种操作的决定。

让我们为我们平台的算法制作决策树的框图：



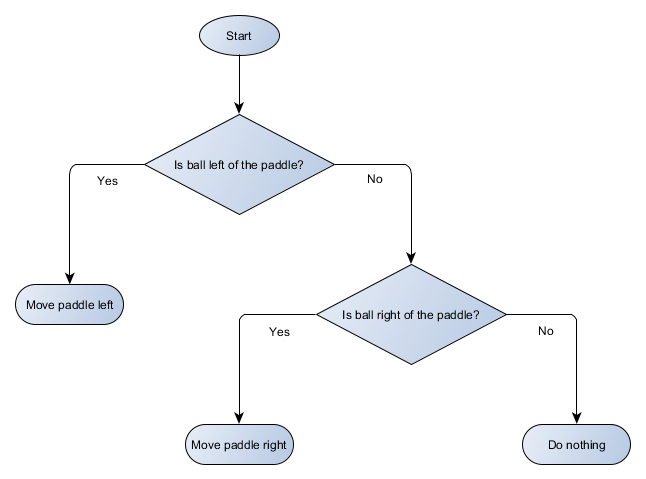
树的每个部分都称为节点-AI使用图论来描述这种结构。 有两种类型的节点：

• 决策节点：基于检查某个条件的情况在两个备选方案之间进行选择，其中每个备选方案均表示为单独的节点。
• 终端节点：代表最终决定的要执行的动作。

该算法从第一个节点（树的“根”）开始。 它要么决定要转到哪个子节点，要么执行存储在该节点中的操作并完成。

如果决策树执行与上一节中的if语句相同的工作，则有什么优势？ 这里有一个通用的系统，其中每个解决方案只有一个条件和两个可能的结果。 这使开发人员可以从代表树中决策的数据创建AI，避免对其进行硬编码。 想象一下表格的形式：



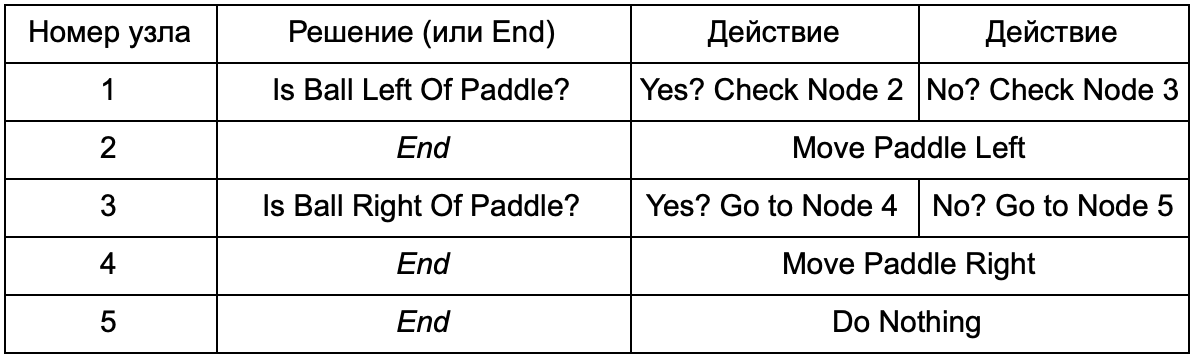
在代码方面，您可以获得读取字符串的系统。 为它们每个创建一个节点，连接基于第二列的决策逻辑和基于第三列和第四列的子节点。 您仍然需要对条件和动作进行编程，但是现在游戏的结构将更加复杂。 在其中，您可以添加其他决策和操作，然后通过简单地编辑带有树定义的文本文件来配置整个AI。 接下来，将文件传输给游戏设计师，后者可以更改行为而无需重新编译游戏和更改代码。

当决策树根据大量示例自动构建时（例如，使用ID3算法），它们非常有用。 这使它们成为用于根据接收到的数据对情况进行分类的有效且高性能的工具。 但是，我们超越了一个简单的系统，供代理选择动作。

情境

我们反汇编了使用预先创建的条件和操作的决策树系统。 AI设计师可以按自己的方式排列树，但他仍然必须依靠对所有树进行编程的编码器。 如果我们可以给设计师工具来创建我们自己的条件或行为该怎么办？

为了防止程序员编写“ Is Ball Left of Paddle”和“ Is Ball Right Of Paddle”条件的代码，他可以创建一个系统，设计人员将在其中记录用于检查这些值的条件。 然后，决策树的数据将如下所示：



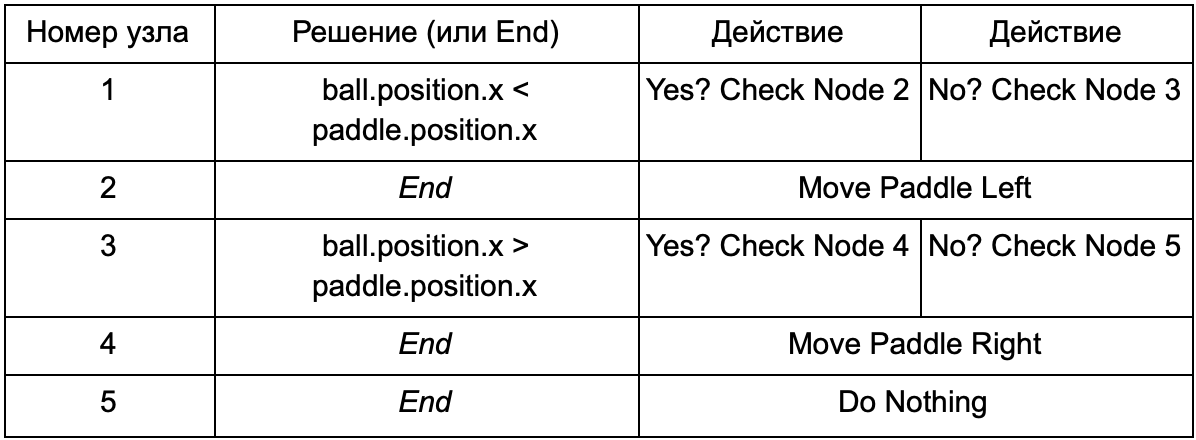
从本质上讲，这与第一个表中的相同，但是内部的解决方案本身具有自己的代码，与if语句的条件部分有点相似。 在代码方面，将在第二列中读取决策节点，但是它没有寻找要满足的特定条件（Is Ball Left Of Paddle），而是计算条件表达式并分别返回true或false。 这是使用脚本语言Lua或Angelscript完成的。 通过使用它们，开发人员可以在游戏中使用对象（球和球拍），并创建将在脚本中可用的变量（ball.position）。 另外，脚本语言比C ++更简单。 它不需要完整的编译阶段，因此非常适合快速调整游戏逻辑，并允许“非编码者”自己创建必要的功能。

在上面的示例中，脚本语言仅用于评估条件表达式，但也可以用于操作。 例如，“向右移板”数据可以成为脚本语句（ball.position.x + = 10）。 这样就可以在脚本中定义动作，而无需编写“向右移动滑杆”。

您甚至可以走得更远，用脚本语言编写完整的决策树。 这将是采用硬编码（hardcoded）条件语句形式的代码，但是它们将位于外部脚本文件中，也就是说，可以在不重新编译整个程序的情况下更改它们。 通常，您可以在游戏过程中直接更改脚本文件，以快速测试不同的AI反应。

事件回应

上面的示例非常适合Pong。 他们不断地执行“感官/思考/行动”循环，并根据世界的最新状况采取行动。 但是在更复杂的游戏中，您需要响应单个事件，而不是立即评估所有事件。 Pong已经是一个不成功的例子。 选择另一个。

想象一下一个射击者，敌人一直静止不动，直到找到玩家为止，然后他们根据自己的“专业化”采取行动：有人将奔向“暗恋”，有人将向远方发起攻击。 这仍然是基本的响应系统-“如果注意到玩家，则执行某些操作”-但可以从逻辑上将其分为“玩家可见事件”（注意到玩家）和反应（选择答案并执行）。

这使我们回到了感官/思考/行为周期。 我们可以对Sense部分进行编码，每一帧都会对其进行检查，以查看玩家的AI是否可见。 如果不是，则什么也不会发生，但是如果看到，则引发Player Seen事件。 该代码将有一个单独的部分，内容为：“发生Player Seen事件时，请执行此操作”，在此处需要参考“思考和行动”部分的答案。 因此，您将对“玩家可见”事件进行设置：“ Andreat”代表“正在成长”的角色，而“ HideAndSnipe”则代表狙击手。 可以在数据文件中创建这些关系以进行快速编辑，而无需重新编译。 在这里，您还可以使用脚本语言。

做出艰难的决定

尽管简单的反应系统非常有效，但在许多情况下它们还不够。 有时有必要根据座席当前正在做的事情来做出各种决定，但是很难想象这是一个条件。 有时有太多条件无法有效地在决策树或脚本中表示它们。 有时，您需要先评估情况将如何变化，然后再决定下一步。 解决这些问题需要更复杂的方法。

有限状态机

有限状态机或FSM（状态机）是一种表示我们的代理当前处于几种可能状态之一，并且他可以从一种状态转移到另一种状态的一种方式。 有一定数量的这种状态-因此命名。 最好的例子就是交通灯。 在不同的地方，不同的照明顺序不同，但是原理是相同的-每个状态代表某种东西（站立，前进等）。 红绿灯在任何给定时间仅处于一种状态，并根据简单规则从一种状态移动到另一种状态。

与NPC在游戏中的故事相似。 例如，在以下情况下采取警卫：

• 巡逻
• 进攻
• 逃离

这些条件可以改变他的状况：

• 如果守卫看到敌人，他会发起进攻。
• 如果警卫进攻，但再也看不到敌人，他将返回巡逻。
• 如果警卫发动进攻，但受了重伤，他便逃走了。

您还可以编写带有警卫状态变量和各种检查的if语句：附近是否有敌人，NPC的健康水平如何？等等。我们再添加一些状态：

• 无为（空闲）-巡逻之间。
• 搜索（搜索）-当发现的敌人消失时。
• 寻求帮助（Finding Help）-当看到敌人时，敌人太强大了，无法独自与他战斗。

他们每个人的选择都是有限的-例如，如果一个卫兵身体不好，他就不会去寻找隐藏的敌人。

最后，庞大的清单“如果<x和y，而不是z>，则<p>”可能会变得太麻烦了，因此我们应该形式化一种方法，使我们能够牢记状态和状态之间的转换。 为此，我们考虑了所有状态，并且在每个状态下，我们列出了到其他状态的所有转换以及它们的必要条件。



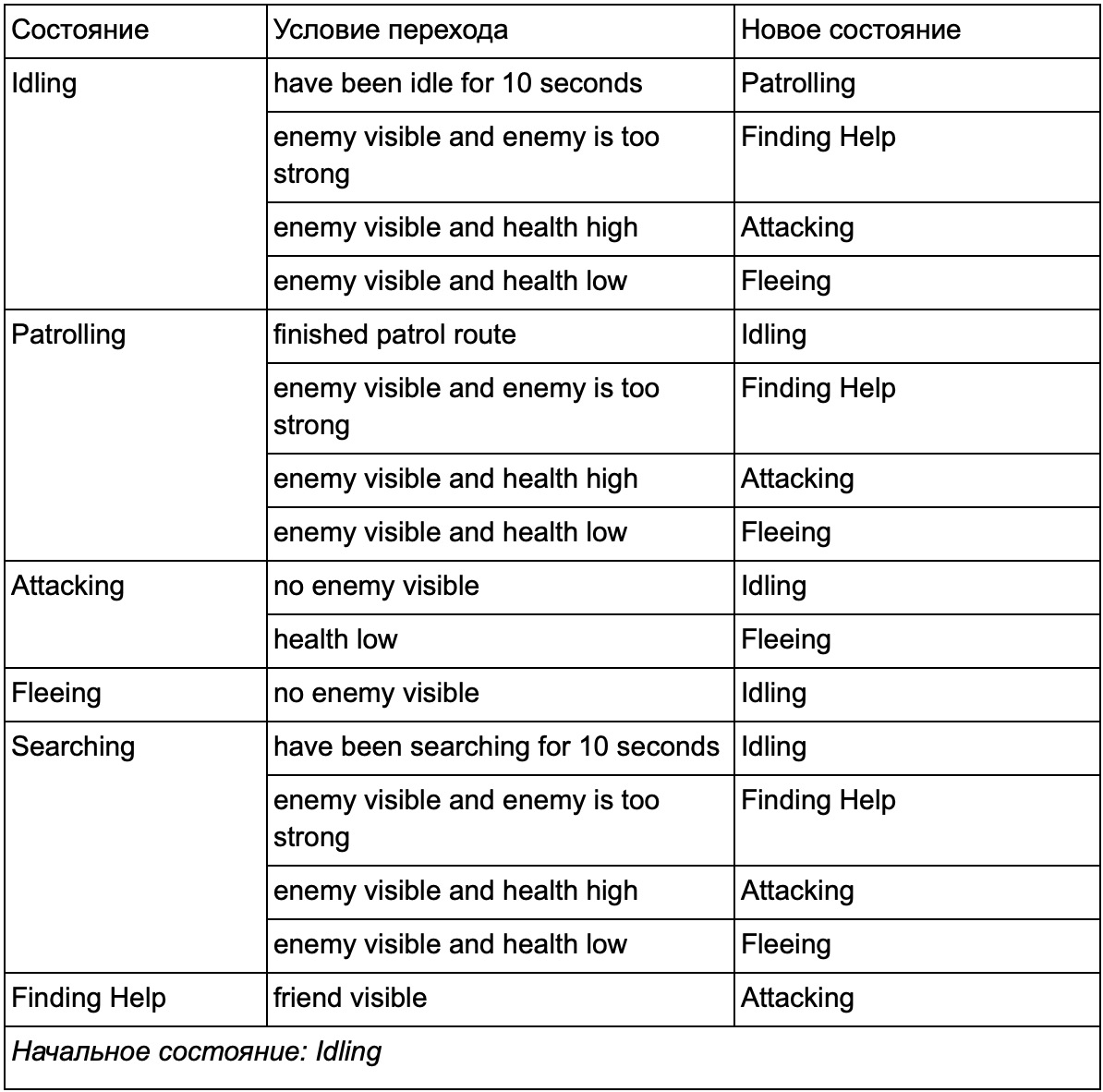
此状态转换表是表示FSM的综合方法。 让我们画一个图，完整地了解NPC的行为如何变化。



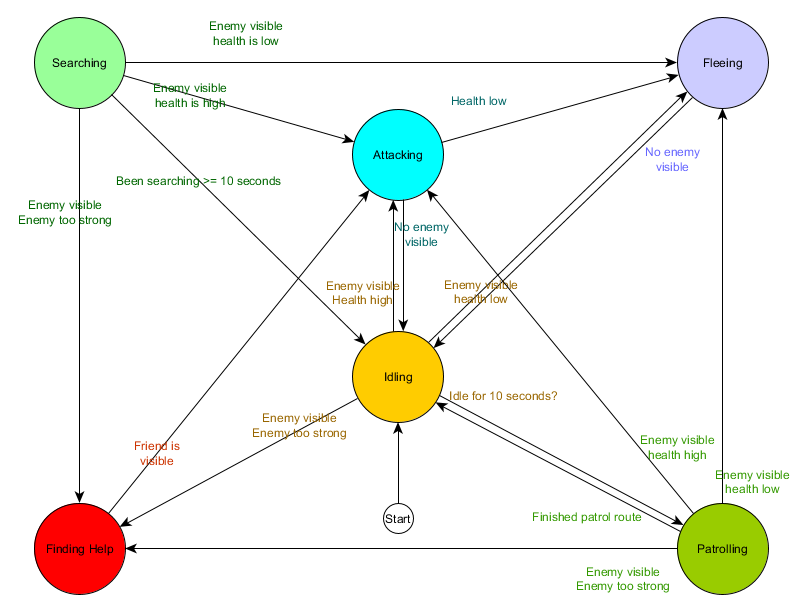
该图表反映了根据当前情况对该代理进行决策的本质。 此外，如果旁边的条件为真，则每个箭头都会显示状态之间的转换。

每次更新时，我们都会检查代理的当前状态，查看转换列表，如果满足转换条件，它将采用新状态。 例如，每个帧都会检查10秒计时器是否已到期，如果已到期，则保护装置将从“空闲”切换为“巡逻”。 以同样的方式，“攻击”状态检查代理的健康状况-如果该代理的状态很低，则进入“逃离”状态。

这是在处理状态转换，但是与状态本身关联的行为又如何呢？ 关于特定状态的实际行为的实现，通常有两种“挂钩”，我们向FSM分配操作：

• 我们针对当前状态定期执行的操作。
• 我们从一种状态转移到另一种状态时所采取的行动。

第一种类型的示例。 巡逻状态每个框架都会使特工沿着巡逻路线移动。 每个帧的攻击状态将尝试开始攻击或​​在可能的情况下进入一种状态。

对于第二种类型，请考虑过渡“如果敌人可见并且敌人太强大，则进入“查找帮助”状态。 代理必须选择去哪里寻求帮助，并保存此信息，以便“查找帮助”状态知道去哪里。 一旦找到帮助，代理将返回到“攻击”状态。 此时，他将要告知盟友有关威胁的信息，因此可能会发生NotifyFriendOfThreat操作。

再说一次，我们可以通过“感官/思考/行为”循环的角度来看待这个系统。 感官转换为转换逻辑使用的数据。 思考-每个状态下都有可用的转换。 行为是通过在州内或州与州之间的过渡阶段定期执行的动作来执行的。

有时，连续轮询过渡条件可能会花费很大。 例如，如果每个特工在每个帧上执行复杂的计算以确定它是否看到敌人并了解是否有可能从巡逻状态切换为攻击，这将花费大量的处理器时间。

世界状况的重要变化可以看作是事件发生时将被处理的事件。 您不必配置FSM来检查过渡条件“我的代理可以看到播放器吗？”每一帧，而是可以配置一个单独的系统以减少检查频率（例如，每秒5次）。 结果是在检查通过时给“玩家可见”。

这被传递给FSM，FSM现在必须进入“玩家可见”事件的接收条件并做出相应的反应。 产生的行为是相同的，除了在回答之前几乎没有察觉到延迟。 但是由于将Sense的一部分分开放在程序的单独部分中，因此性能变得更好。

分层有限状态机

但是，使用大型FSM并不总是很方便。 如果要通过用单独的MeleeAttacking（近战）和RangedAttacking（远程）替换攻击状态来扩展攻击状态，则必须更改从所有其他状态到攻击状态（当前和将来）的转换。

当然，您已经注意到在我们的示例中有很多重复的过渡。 怠速状态下的大多数过渡与巡逻状态下的过渡相同。 最好不要重复，特别是如果我们添加更多类似的状态。 将空转和巡逻分组为通用标签“非战斗”是有意义的，在该标签下，只有一组通用的过渡到战斗状态的过渡。 如果我们将此标签显示为状态，则“空闲”和“巡逻”将成为子状态。 为新的非战斗子状态使用单独的转换表的示例：

主要条件：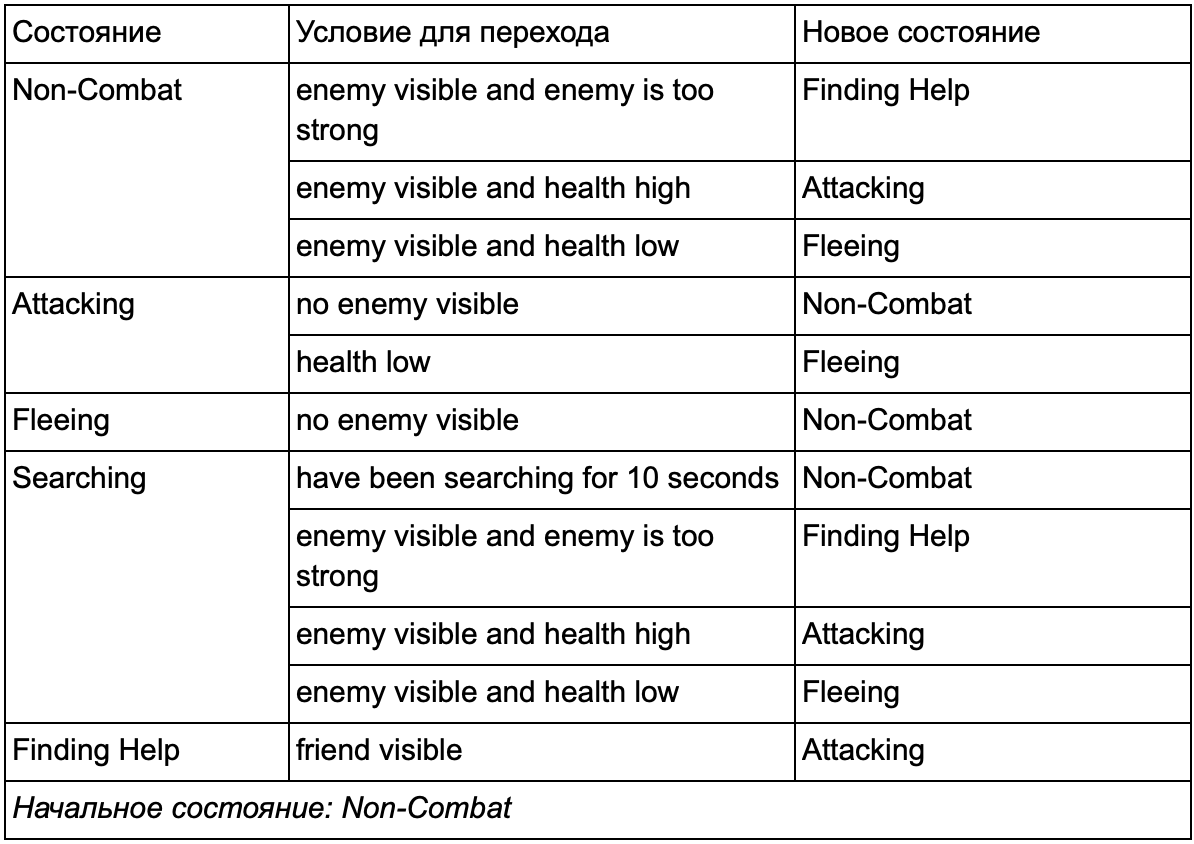


非战斗状态：


并以图表形式：



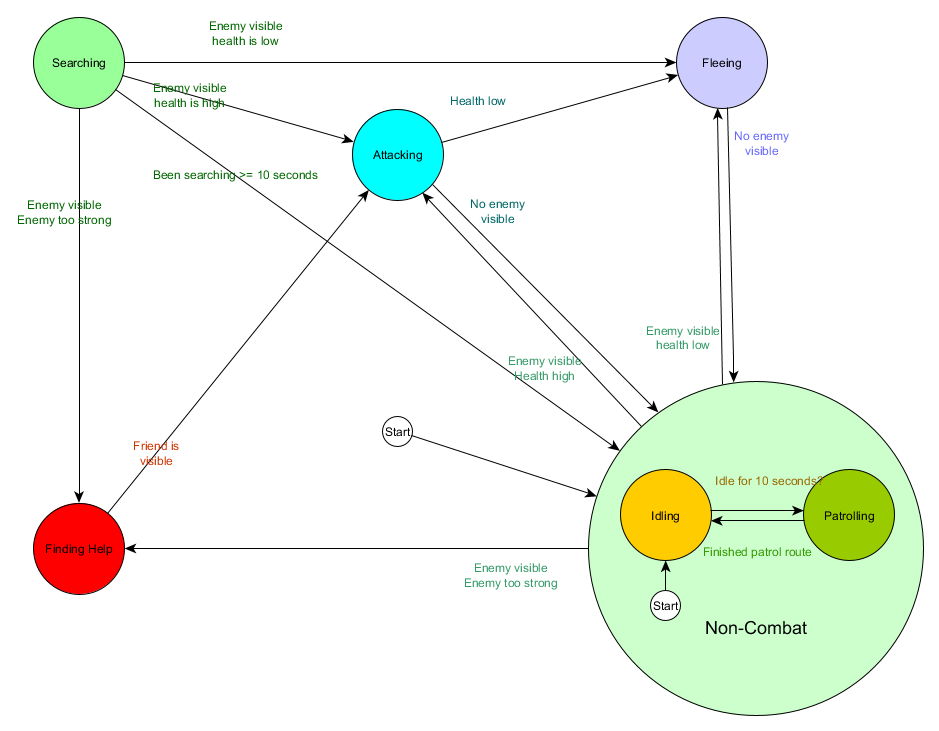
这是相同的系统，但具有新的非战斗状态，其中包括空转和巡逻。 对于每个包含带有子状态的FSM的状态（这些子状态又包含它们自己的FSM-依您需要的程度依次类推），我们得到了层次有限状态机或HFSM（层次状态机）。 将非战斗状态分组后，我们切出了一堆多余的过渡。 对于具有共同过渡的任何新州，我们都可以这样做。 例如，如果将来我们将“攻击”状态扩展到“近战攻击”和“导弹攻击”状态，则它们将是根据与敌人的距离和弹药的存在而相互交叉的子状态。 结果，可以用最少的重复转换来表示行为的复杂模型和行为的子模型。

HFSM . , , . , . . , , . , 25%, , , , — . 25% 10%, .

, « », , . .

, : «» , , , . :

• : Succeeded ( ), Failed ( ) Running ( ).
• . Decorator, . Succeed, .
• , , Running .

. HFSM :



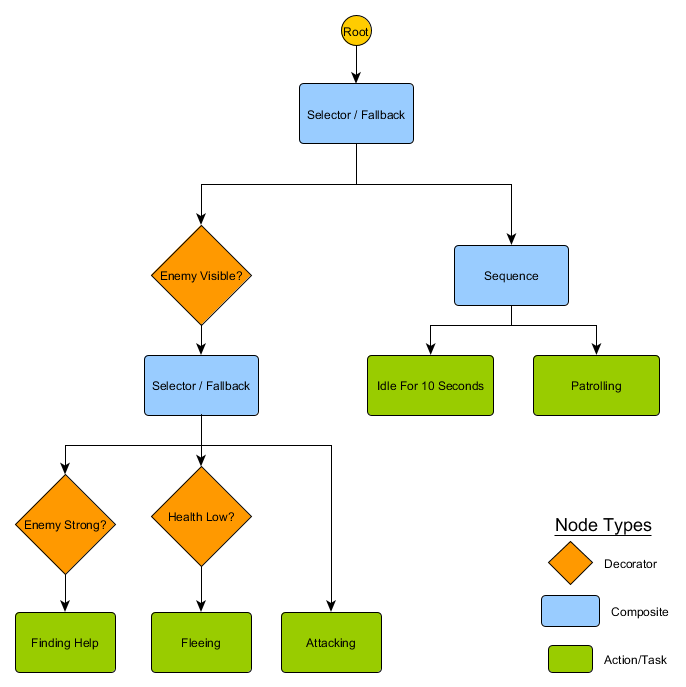
Idling/Patrolling Attacking . , , Fleeing, , — Patrolling, Idling, Attacking .



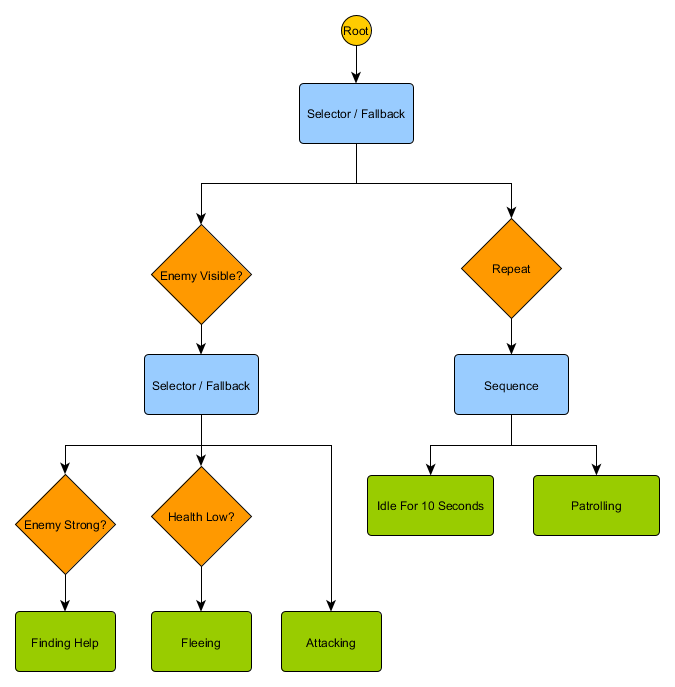
— , . , — , ? , — , Idling 10 , , ?

. , . , .

Utility-based system

. , , . , , .

Utility-based system (, ) . , , , . — , .

, . FSM, , , . , ( , ). , .

— , 0 ( ) 100 ( ). , . :



— . . , , , Fleeing, FindingHelp . FindingHelp . , 50, . .

, . . , Fleeing , , Attacking , . - Fleeing Attacking , , . , , FSM.

. . The Sims, , — «», . , , EatFood , , , EatFood .

, Utility-based system , . . , Utility , , .

, , , . ? , , , , ? .

管理学

, , , . , , . . Sense/Think/Act, , Think , Act . , , . — , . , , . :

desired_travel = destination_position – agent_position

2D-. (-2,-2), - - (30, 20), , — (32, 22). , — 5 , (4.12, 2.83). 8 .

. , , 5 / ( ), . , .

— , , , . . steering behaviours, : Seek (), Flee (), Arrival () . . , , , .

. Seek Arrival — . Obstacle Avoidance ( ) Separation () , . Alignment () Cohesion () . steering behaviours . , Arrival, Separation Obstacle Avoidance, . .

, — , - Arrival Obstacle Avoidance. , , . : , .

, , - .

Steering behaviours ( ), — . pathfinding ( ), .

— . - , , . . , ( , ). , Breadth-First Search BFS ( ). ( breadth, «»). , , — , , .



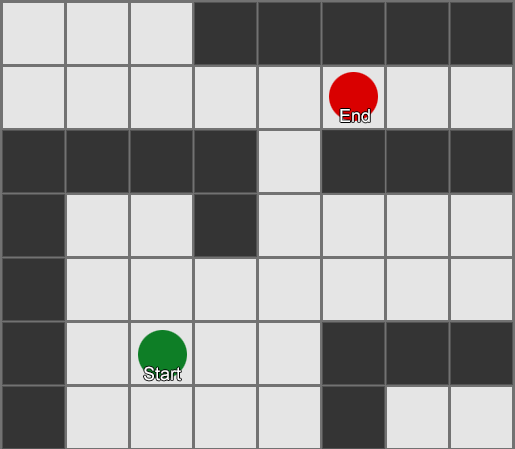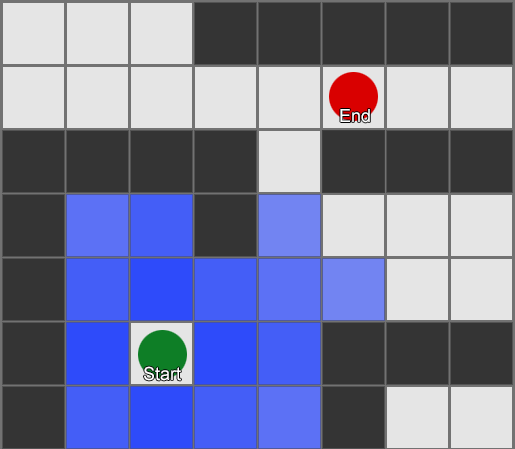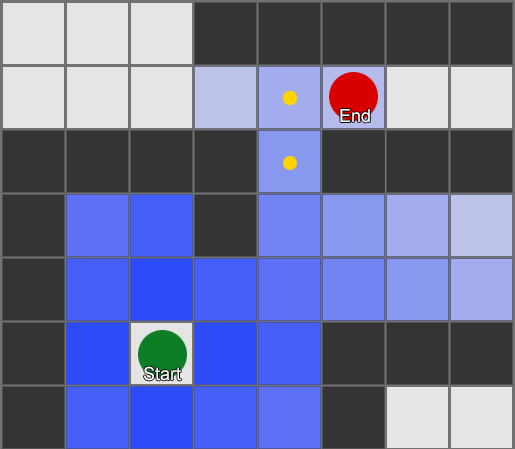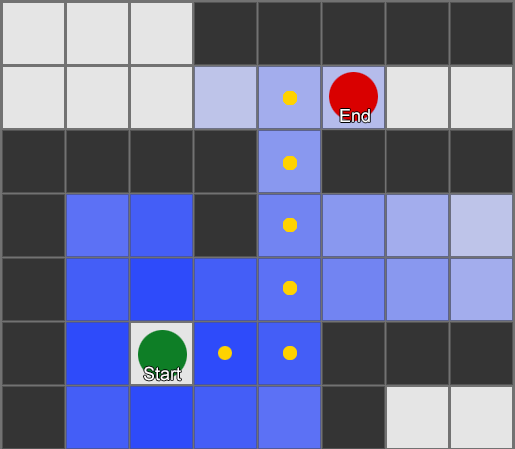
, . (, pathfinding) — , , .

, , steering behaviours, — 1 2, 2 3 . — , — . - .

BFS — «» , «». A* (A star). , - ( , ), , , . , — «» ( ) , ( ).



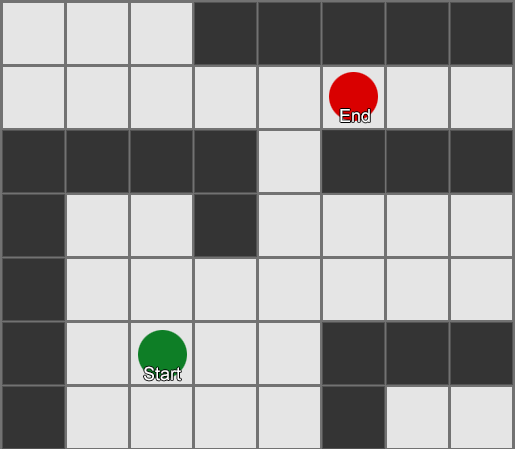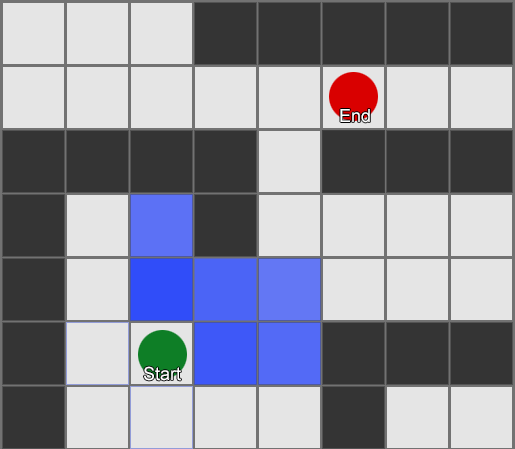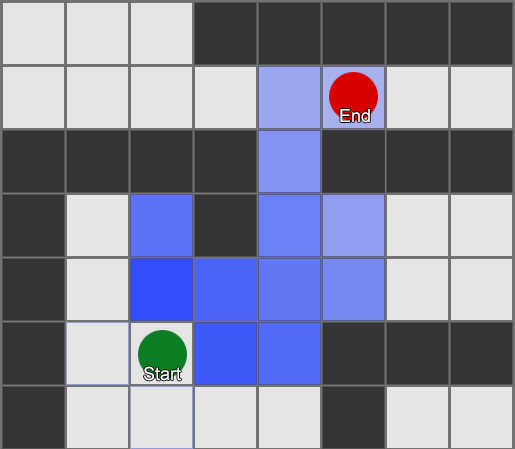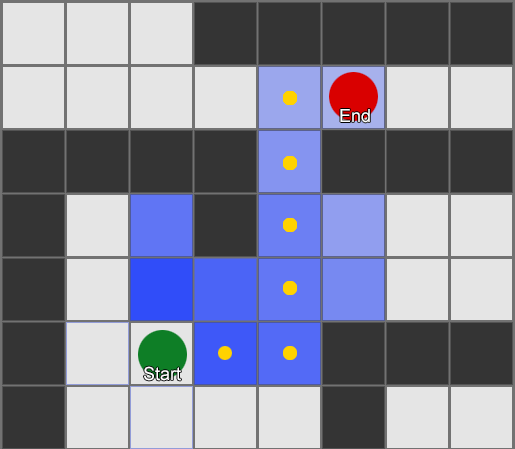
, , , . , BFS, — .

但是，大多数游戏并非都摆在网格上，而且通常不能在不影响真实性的情况下完成。 需要妥协。 正方形应该是多少尺寸？ 太大-他们将无法正确想象小的走廊或转弯，或者太小-搜索的正方形过多，最终将花费大量时间。

首先要了解的是，网格为我们提供了连接节点的图形。 A *和BFS算法实际上适用于图，根本不关心我们的网格。 我们可以将节点放置在游戏世界中的任何地方：如果任何两个相连的节点之间以及起点和终点以及至少一个节点之间存在连接，该算法将像以前一样工作。 这通常被称为航路点系统，因为每个节点都代表着世界上的重要位置，可以是任何数量的假设路径的一部分。


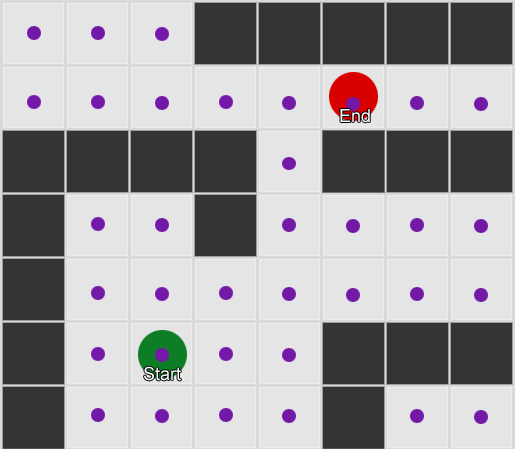例1：每个方块都有一个结。 搜索从代理所位于的节点开始，并在所需正方形的节点处结束。


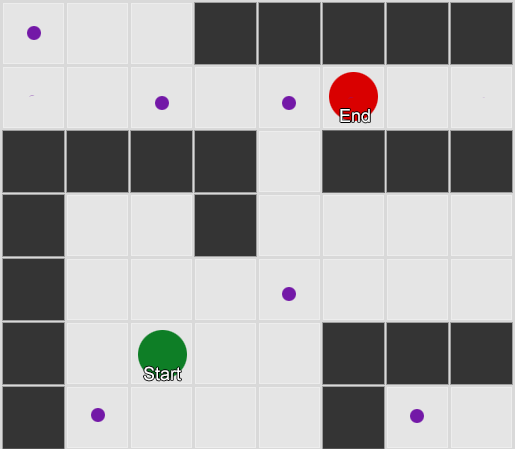示例2：一组较小的节点（航点）。 搜索开始于代理平方，经过所需数量的节点，然后继续到达目的地。

这是一个完全灵活且功能强大的系统。 但是在确定航路点的位置和方式时需要谨慎，否则座席可能根本看不到最近的点，也无法启动路径。 如果我们可以根据世界的几何形状自动设置航点，将会更加容易。

然后出现导航网格或导航网格。 这通常是一个2D三角形网格，覆盖了世界的几何图形-允许代理人行走的任何地方。 网格中的每个三角形都成为图形中的一个节点，并具有多达三个相邻的三角形，这些三角形成为图形中的相邻节点。

这张图片是Unity引擎的示例-他分析了世界上的几何图形并创建了导航网格（屏幕截图中的淡蓝色）。 导航网格中的每个多边形都是代理可以站立或从一个多边形移动到另一个多边形的区域。 在此示例中，多边形要比其所在的地板小-制作时要考虑到代理的尺寸，该尺寸将超出其标称位置。



我们可以再次使用A *算法搜索通过此网格的路线。 这将为我们提供一条几乎完美的路线，其中考虑了所有几何图形，并且不需要额外的节点和航路点。

寻路是一个太广泛的话题，关于这篇文章的哪一部分还不够。 如果您想更详细地研究它，那么Amit Patel的站点将对此提供帮助。

规划中

我们通过寻路确保有时仅选择方向并移动是不够的-我们必须选择一条路线并转几圈才能到达所需的目的地。 我们可以总结一下这个想法：实现目标不仅是下一步，而且是一个完整的序列，有时您需要向前看几个步骤以找出第一步应该是什么。 这称为计划。 寻路可以被认为是几个规划中的一项。 从我们的“感官/思考/行动”周期的角度来看，这是“思想”部分计划未来的“行动”部分的地方。

让我们看一下棋盘游戏《 Magic：The Gathering》的示例。 我们首先拿着这样的卡片：

• 沼泽-提供1点黑色法力值（地球地图）。
• 森林-提供1点绿色法力值（地球地图）。
• 逃亡向导-需要1点蓝色魔力才能召唤。
• 精灵神秘主义者-需要1点绿色魔力才能召唤。

我们将忽略剩下的三张牌，以简化操作。 根据规则，玩家每回合可以玩一张卡牌，他可以“点击”该卡牌从中抽取法力，然后根据法力值使用咒语（包括召唤生物）。 在这种情况下，人类玩家知道您需要扮演森林，“点击” 1个绿色法术力，然后呼叫精灵神秘主义者。 但是，您如何猜测游戏AI？

轻松规划

简单的方法是依次尝试每个动作，直到找到合适的动作为止。 看着卡，AI会看到Swamp可以玩什么。 并播放。 这个回合还有其他动作吗？ 他不能召唤精灵神秘法师或逃亡巫师，因为他们的召唤分别需要绿色和蓝色法力，而沼泽只提供黑色法力。 而且他将无法扮演Forest，因为他已经扮演过Swamp。 因此，游戏AI遵守规则，但效果不佳。 可以改进。

规划人员可以找到将游戏带入所需状态的动作列表。 正如路径上的每个正方形都有邻居（在寻路中）一样，计划中的每个动作也都有邻居或后继。 我们可以搜索这些操作和后续操作，直到达到所需状态为止。

在我们的示例中，期望的结果是“如果可能，召唤一个生物”。 在移动开始时，我们仅看到游戏规则允许的两种可能的动作：

1.玩Swamp（结果：游戏中的Swamp）
2.玩森林（结果：游戏中的森林）

取决于游戏规则，所采取的每个动作都可能导致进一步的动作并关闭其他动作。 想象一下我们玩过沼泽-下一步将删除沼泽（我们已经玩过），也将删除森林（因为根据规则，您每回合可以玩一张土地地图）。 在那之后，AI增加了下一步-获得1点黑色法术力，因为没有其他选择。 如果他走得更远并且选择了“轻拍沼泽”，他将获得1个单位的黑色法力值，并且无法对其进行任何处理。

1.玩Swamp（结果：游戏中的Swamp）
1.1“抽头”沼泽（结果：“抽头”沼泽，黑法力值+1单位）
无可用操作-结束
2.玩森林（结果：游戏中的森林）

行动清单很短，我们陷入了僵局。 对下一步重复该过程。 我们玩森林游戏，打开动作“获得1点绿色法术力”，这反过来又将打开第三个动作-Elvish Mystic的召唤。

1.玩Swamp（结果：游戏中的Swamp）
1.1“抽头”沼泽（结果：“抽头”沼泽，黑法力值+1单位）
无可用操作-结束
2.玩森林（结果：游戏中的森林）
2.1“轻击”森林（结果：森林“轻击”，+ 1绿色法术力单位）
2.1.1召唤精灵秘法师（结果：游戏中的精灵秘法师，绿色法力值-1单位）
无可用操作-结束

最后，我们检查了所有可能的动作，并找到了一个计划来调用该生物。

这是一个非常简化的示例。 建议选择最佳方案，而不要选择任何符合某些标准的方案。 通常，您可以根据最终结果或实施的总收益评估潜在计划。 您可以在玩地球地图时加1点，在挑战生物时加3点。 要玩“沼泽”游戏，您将得到1分的计划。 并打出森林→轻按森林→召唤精灵神秘主义者-他将立即获得4分。

这就是“魔术：聚会”中计划的工作原理，但根据相同的逻辑，它也适用于其他情况。 例如，移动棋子为主教腾出空间来下棋。 或在墙后掩护以安全地向XCOM射击。 通常，您会明白这一点。

改善计划

有时，潜在的动作太多，无法考虑所有可能的选择。 回到魔术：聚会的例子：假设在游戏中和您的手上有几张土地和生物牌-可能的组合动作数为数十。 有几种解决方案。

第一种方法是向后链接。 与其对所有组合进行分类，不如从最终结果开始并尝试查找直接路线。 而不是从树的根到特定叶的路径，我们沿相反的方向移动-从叶到根。 此方法更简单，更快捷。

如果对手的生命值为1，则可以找到“造成1个或更多单位伤害”的计划。 为此，必须满足许多条件：

1.伤害可能是由咒语造成的-它应该在手上。
2.要施放法术，需要法力值。
3.要获得法力值，您需要打一张土地牌。
4.要玩地球牌-您需要手拿它。

另一种方法是最佳优先搜索。 我们没有选择所有路径，而是选择了最合适的路径。 大多数情况下，此方法会提供最佳计划，而不会产生不必要的搜索成本。 *是最好的优先搜索形式-从一开始就探索最有希望的路线，他已经可以找到最佳方法而不必检查其他选项。

最佳优先搜索的一种有趣且日益流行的选择是“蒙特卡洛树搜索”。 该算法不会在选择每个后续操作时猜测哪个计划比其他计划更好，而是在每个步骤中选择随机后继，直到到达终点为止（当计划导致胜利或失败时）。 然后，将最终结果用于增加或减少先前选项的重量等级。 连续多次重复此过程，即使情况发生变化（如果对手采取措施阻止玩家），该算法也可以很好地估算出哪个下一步更好。

没有面向目标的行动计划或GOAP（面向目标的行动计划），有关游戏中计划的故事就不会成立。 这是一种广泛使用和讨论的方法，但是除了一些独特的细节外，它本质上是我们前面提到的反向链接方法。 如果任务是“消灭玩家”，而玩家处于掩护之下，则计划可能是这样的：用手榴弹消灭→得到它→放下它。

通常有几个目标，每个目标都有其自己的优先级。 如果不能完成具有最高优先级的目标（由于玩家不可见，没有任何动作组合可创建“摧毁玩家”的计划），则AI将返回优先级较低的目标。

训练与适应

我们已经说过，游戏AI通常不使用机器学习，因为它不适合实时管理代理。 但这并不意味着您不能从该领域借任何东西。 我们希望射击游戏中有这样的对手，我们可以从中学到一些东西。 例如，找出地图上的最佳位置。 或格斗游戏中的对手会阻止玩家经常使用的组合技巧，从而激励其他人使用。 因此，在这种情况下的机器学习非常有用。

统计和概率

在继续介绍复杂的示例之前，我们将通过进行一些简单的测量并使用它们来做出决策来估计我们可以走多远。 例如，一项实时策略-我们如何确定玩家是否可以在游戏的前几分钟内发起攻击，以及如何为此做出准备？ 我们可以研究玩家的过去经验，以了解未来的反应。 首先，我们没有这样的初始数据，但是我们可以收集它们-每当AI与某人对抗时，他就可以记录第一次攻击的时间。 经过几次练习后，我们将获得玩家将来攻击的平均时间。

平均值存在一个问题：如果玩家“决定” 20次并且玩慢20次，则必要的值将位于中间的某个位置，这将无法为我们提供任何有用的信息。 一种解决方案是限制输入-您可以考虑最后20件。

假设玩家过去的喜好在将来会相同，则使用类似的方法来评估某些动作的可能性。 如果玩家用火球攻击我们五次，用闪电攻击两次，一次进行近身格斗，那么显然他更喜欢火球。 我们推断出使用各种武器的可能性：火球= 62.5％，闪电= 25％，近战= 12.5％。 我们的游戏AI需要为防火做好准备。

另一个有趣的方法是使用朴素贝叶斯分类器（朴素贝叶斯分类器）来研究大量输入数据并对情况进行分类，以便AI以正确的方式做出响应。 贝叶斯分类器以使用电子邮件垃圾邮件过滤器而闻名。 他们在那里研究单词，将它们与单词出现较早的位置（是否存在垃圾邮件）进行比较，并得出有关来信的结论。 即使输入更少，我们也可以这样做。 根据AI看到的所有有用信息（例如，创建了哪些敌方单位，他们使用的咒语，或他们探索的技术）以及最终结果（战争或和平，“粉碎”或防御等）-我们将选择所需的AI行为。

所有这些培训方法都足够了，但是建议根据测试数据使用它们。 AI将学习如何适应您的游戏测试人员所使用的各种策略。 发行后适应玩家的AI可能变得太可预测，反之亦然，太复杂而无法获胜。

基于价值的适应

根据游戏世界的内容和规则，我们可以更改影响决策的价值集，而不仅仅是使用输入数据。 我们这样做：

• 让AI收集有关游戏过程中的世界状况和关键事件的数据（如上所述）。
• 让我们根据此数据更改一些重要的值。
• 我们基于对这些值的处理或评估来实现决策。

例如，一个代理商有几个房间，可以在地图上选择第一人称射击游戏。 每个房间都有自己的价值，这决定了访问的理想程度。 AI根据值的价值随机选择要去的房间。 然后，代理会记住他在哪个房间被杀，并降低其价值（他将返回该房间的可能性）。 对于相反的情况类似-如果代理破坏了许多对手，那么房间的价值就会增加。

马尔可夫模型

如果我们使用收集的数据进行预测怎么办？ 如果我们记得在一段时间内看到玩家的每个房间，我们将预测玩家可以进入哪个房间。 通过跟踪并记录玩家在房间中的移动（值），我们可以预测它们。

我们来三个房间：红色，绿色和蓝色。 以及观看比赛时我们记录的观察结果：



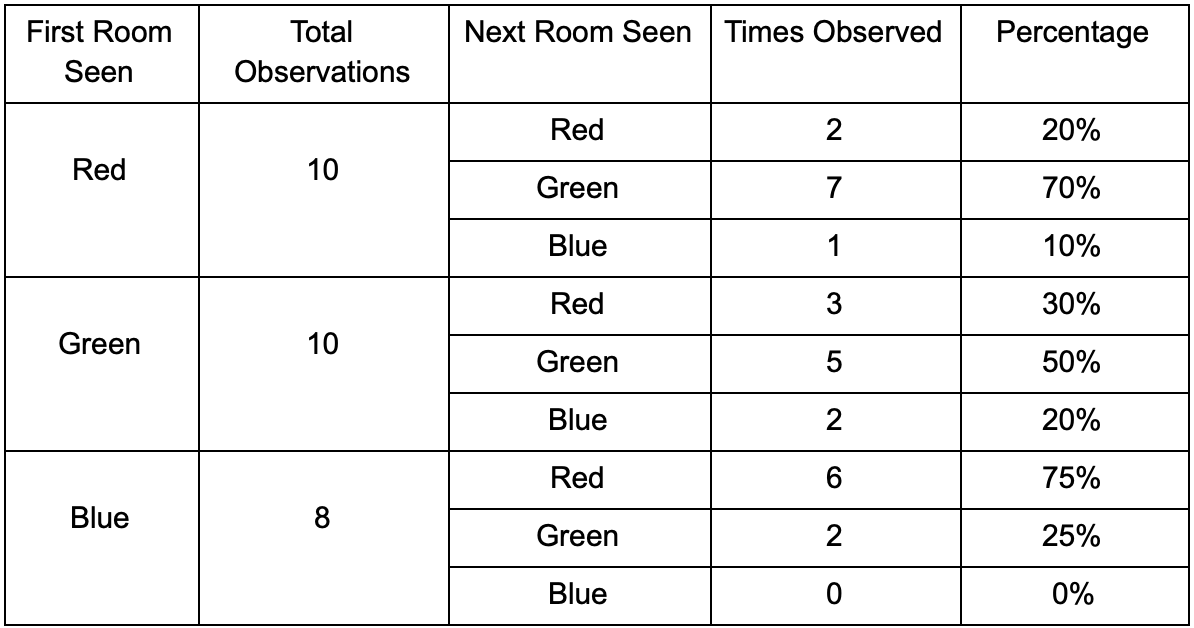
每个房间的观察次数几乎相等-我们仍然不知道在哪里埋伏一个好地方。 由于在地图上均匀出现的玩家的重生也使统计数据的收集变得复杂。 但是他们出现在地图上之后输入的下一个房间的数据已经有用。

可以看出，绿色房间适合玩家-红色的大多数人都喜欢它，其中50％留在那里。 相反，蓝色房间并不受欢迎，几乎从未有人光顾过，如果这样的话，它就不会流连忘返。

但是数据告诉我们一些更重要的事情-当玩家在蓝色房间时，我们最有可能看到他的下一个房间将是红色，而不是绿色。 尽管事实是绿色的房间比红色的房间更受欢迎，但是如果玩家是蓝色的，情况就会改变。 下一个状态（即玩家将进入的房间）取决于先前的状态（即玩家现在所在的房间）。 由于对依赖关系的研究，比起简单地彼此独立地计算观测值，我们将做出更准确的预测。

根据过去状态数据预测未来状态称为Markov模型，此类示例（包含会议室）称为Markov链。 由于模型表示连续状态之间发生变化的概率，因此它们在视觉上显示为FSM，且在每个过渡附近都有发生的可能性。 以前，我们使用FSM表示代理所位于的行为状态，但是此概念适用于任何状态，无论它是否与代理相关。 在这种情况下，状态代表代理商所占据的房间：



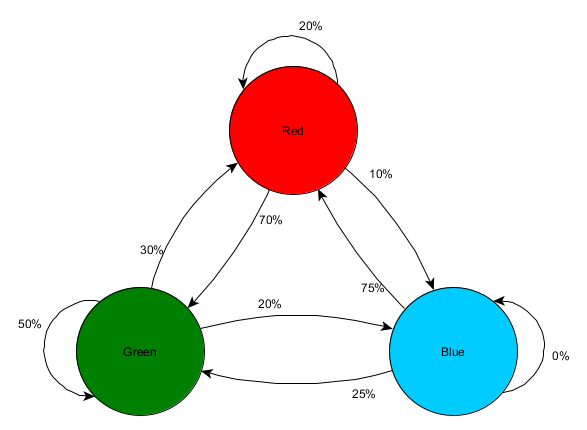
这是状态变化相对概率表示的简单形式，为AI提供了预测下一个状态的机会。 您可以预测前进的几步。

如果玩家在绿色房间中，那么下一次观察期间他有50％的机会会留在绿色房间中。 但是他甚至在那之后仍会在那里的可能性是什么？ 经过两次观察，玩家不仅有机会留在果岭房间，而且有机会离开并返回。 这是带有新数据的新表：



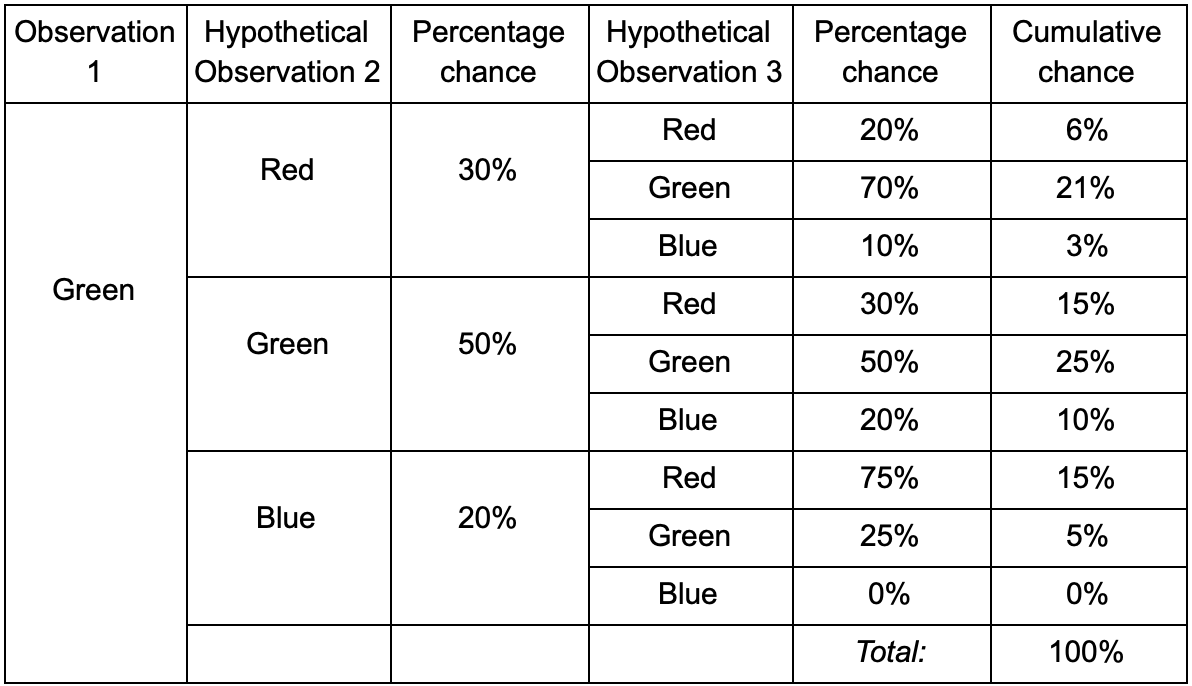
它表明，经过两次观察，在绿色房间中看到玩家的机会将为51％-21％，他来自红色房间，其中5％，该玩家将访问它们之间的蓝色房间，而25％，该玩家不会将离开绿色房间。

表格只是可视化工具-过程仅需要在每个步骤中增加概率。 这意味着您可以通过一项修订来展望未来：我们假设进入房间的机会完全取决于当前房间。 这称为“马尔可夫财产”-未来状态仅取决于现在。 但这并不完全准确。 玩家可以根据其他因素做出决定：健康水平或弹药数量。 由于我们没有固定这些值，因此我们的预测将不太准确。

克

- ? 一样的东西！ , , -.

— (, Kick, Punch Block) . , Kick, Kick, Punch, SuperDeathFist, , .


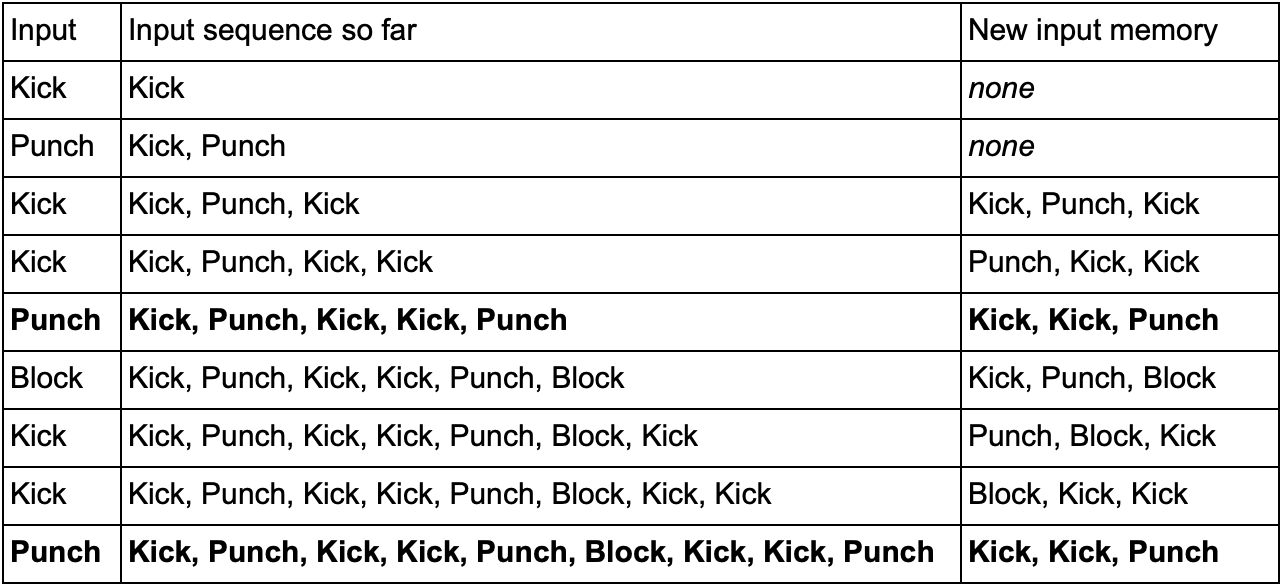
( , SuperDeathFist.)

, Kick, Kick, , Punch. - SuperDeathFist , .

N- (N-grams), N — . 3- (), : . 5- .

N-. N , . , 2- () Kick, Kick Kick, Punch, Kick, Kick, Punch, SuperDeathFist.

, , . Kick, Punch Block, 10-, 60 .

— « / » , . 3- N- , ( N-) , — . Kick Kick Kick Punch. , , , . , , - .

结论

. , .

. , , . , :

• , ,
• / (minimax alpha-beta pruning)
• (, )
• ( , )
• ( )
• ( , anytime, timeslicing)

- :

1. GameDev.net , .
2. AiGameDev.com .
3. The GDC Vault GDC AI, .
4. AI Game Programmers Guild .
5. , , YouTube- AI and Games .

:

1. Game AI Pro , , .

Game AI Pro: Collected Wisdom of Game AI Professionals
Game AI Pro 2: Collected Wisdom of Game AI Professionals
Game AI Pro 3: Collected Wisdom of Game AI Professionals

2. AI Game Programming Wisdom — Game AI Pro. , .

AI Game Programming Wisdom 1
AI Game Programming Wisdom 2
AI Game Programming Wisdom 3
AI Game Programming Wisdom 4

3. Artificial Intelligence: A Modern Approach — . — .