一个主要的数学成就是由一小组研究人员发现的Zimmer假设。
对于具有更高对称尺寸的光栅，并非总是可能转移到低于等级的尺寸Robert Zimmer的成功可以用很多方式来定义。 自2006年以来，他一直
担任芝加哥大学的校长，成为头条新闻，为资助和发表
文章以支持校园言论自由找到了九位数的资金。 但是在成为大学校长之前，他是一名数学家。 在离开认真的研究很久之后，他发起的研究计划终于给出了他的结果。
一年前，三位数学家
证明了齐默尔的假说与几何空间具有某种类型对称性的情况有关。 他们的证明已成为近年来最大的数学成就之一。 这终结了齐默尔在1970年代末和1980年代初激烈的精神活动期间出现的问题。
齐默说：“我想说我每天晚上上床睡觉五年都是对此事的想法，所以我被它迷住了，很高兴看到人们如何解决它。”
通常，几何尺寸空间越大，其中的对称性就越大。 通过研究存在于二维平面上的圆和在三个维度上延伸的球，可以想象得到这一点：旋转球的方法多于旋转圆的方法。 附加的球尺寸会产生附加的对称性。
齐默尔的猜想是指一种特殊的对称性，称为高阶格。 她询问几何空间的测量是否限制了这种类型的对称性的使用。 这项新著作的作者-芝加哥大学的
Aaron Brown和
Sebastian Hurtado-Salazar以及印第安纳大学的
David Fisher-显示，测量次数少于特定的对称性。 因此，他们证明了齐默尔假说的正确性。
现任芝加哥大学校长的罗伯特·齐默（Robert Zimmer）提出了一种假设，以他40年前的名字命名他们的工作回答了一个重要且长期存在的问题，为研究许多其他问题开辟了新的途径。 它还揭示了几何空间的内在属性。 对称性是此类空间最简单的属性之一。 新的工作说对称性可以存在于一种类型的空间中，而不能存在于其他类型的空间中。 经过数十年的停机时间，这项成就得以实现。
芝加哥大学的数学家艾米·威尔金森（Amy Wilkinson）说：“这种假设看起来可以使人们长时间忙碌。” “而且他们相对简单地摧毁了这个问题。”
满足对称性
对称性是儿童在数学中遇到的第一个几何概念。 他们用自己的双手，学会了可以旋转，翻转和移动表格，最后得到与开始时相同的表格。 由于变化而保持对象的形状会产生一定的内部满足感-这暗示着宇宙中存在着更深层次的秩序。
数学家有他们自己的形式语言来研究对称性。 这使他们有机会以简洁的方式讨论在给定几何空间中适用的各种对称性。
例如，正方形具有八个对称性-八种翻转或旋转方式，再次得到正方形。 圆可以旋转任意角度。 她有无限多个对称性。 数学家收集给定几何对象或空间的所有对称性，并将它们打包成一个“组”。
团体本身很有趣。 它们通常是由于研究某些几何空间而出现的，但有时它们出现在与几何完全无关的上下文中。 例如，组可以形成数字集（例如，从数字中减去5或5时具有一定的对称性）。
齐默说：“原则上，一个群体可以表现为完全不同的事物的对称。”
对称性比我们在学校学习的形式要多。 考虑例如晶格的对称性。 最简单的晶格是二维网格。 在平面上，可以将格子向上，向下，向左，向右移动任意数量的正方形，从而获得看起来与原始格子完全相同的格子。 您还可以通过任意数量的单个单元格反映网格。 带有光栅的空间具有无限多个不同的光栅对称性。
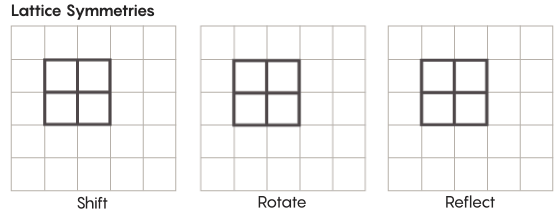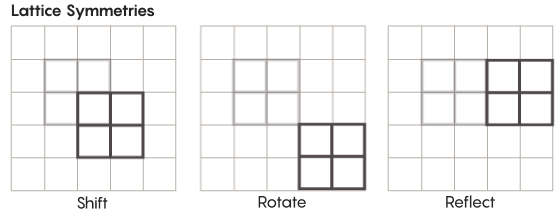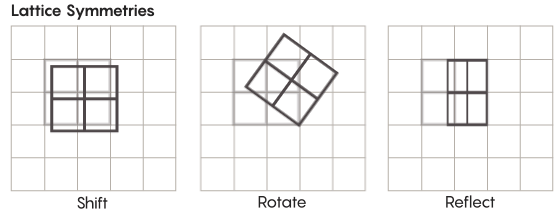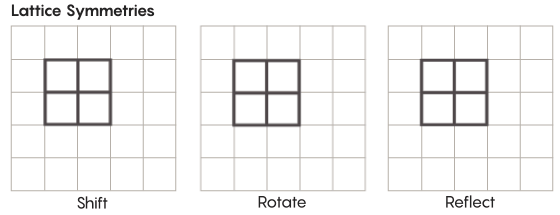
格可以以任何数量的维度存在。 在三维空间中，晶格可能由立方体而不是正方形组成。 在四个或更多个维度上，将无法显示晶格，但是它的工作方式相同。 数学家可以准确地描述它。 Zimmer假设的感兴趣的组包括“较高等级”的晶格，或某些维数较大的空间中的晶格。 库尔塔多·萨拉查（Khurtado-Salazar）说：“即使不给我看，这个奇怪的格子也将非常漂亮。” “在我看来，看着她会很好。”
在20世纪，数学家在各种条件下发现了这些组-不仅在几何上，而且还在数论，逻辑和计算机科学上。 打开新的组，顺理成章地问一个问题-什么样的空间具有这种对称集？
有时，组显然不可能匹配空间。 可以很快理解圆的一组对称性不能应用于正方形。 将正方形旋转10度，您将不会获得原始正方形。 但是，具有无限数量的对称性的组和具有许多维的空间的混合使得难以确定该组的适用性。
齐默说：“在更大范围内转向更复杂的团队时，这些问题变得非常复杂。”
间接连接
想象对称，我们想象整个形状的旋转-例如，一个正方形旋转了90度。 但在基本层面上，对称性取决于移动点。 空间的对称变换意味着您需要利用空间的每个点，然后将其移动到其他点。 从这个意义上讲，将正方形旋转90度实际上意味着您需要获取正方形的每个点并将其旋转90度，以使其不在开始的边缘上。
大卫·费舍尔移动点的问题可以或多或少地严格解决。 最熟悉的对称变换-正方形相对于对角线的反射或其旋转90度-非常严格。 严格意义上讲，它们不要混淆。 反射前为顶点的点在反射后仍为顶点（它们变为不同的顶点），反射后构成直边的点仍构成直边（略有不同）。
对称变换的类型较少严格，也较灵活，在Zimmer假设的背景下它们很有趣。 在这样的转换中，积分会更强烈地改变其组织； 转换后，它们不一定会保留以前的联系。 例如，您可以沿正方形的周长移动正方形的每个点三个长度的长度-这满足了对称变换的基本要求，即简单地将空间中的每个点移到另一个位置。 该证明的合著者亚伦·布朗（Aaron Brown）描述了这些更自由形式的转换在球的背景下可能如何显示。
“您可以将北极和南极朝相反的方向扭转。 然后，两点之间的距离会增加，”布朗说。
对于网格，您可以将其弯曲，在某些位置拉伸然后在其他位置挤压，而不是简单地沿平面移动，以使变换后的网格不再与原始网格重叠。 这样的变换不太严格，被称为微同
态 。
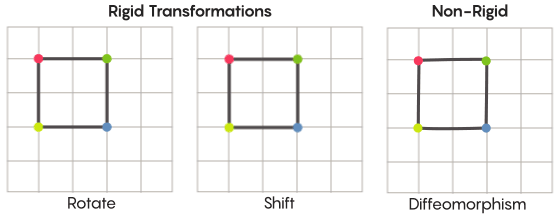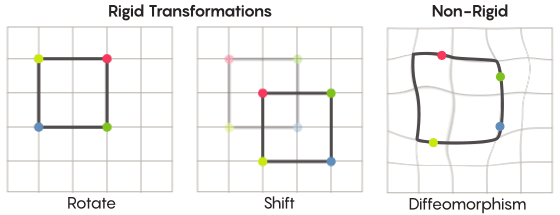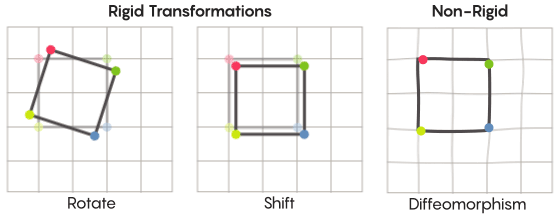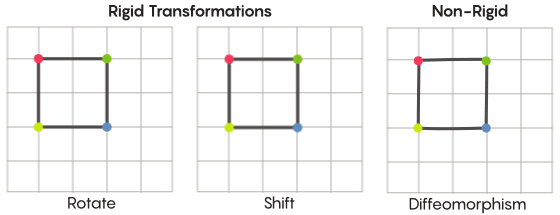
Zimmer有充分的理由在他的假设中使用这种不太严格的对称形式。 与该假设相关的最高等级的特殊晶格最早是由
格里高里·亚历山德罗维奇·马古利斯 （
Grigory Alexandrovich Margulis）在1960年代研究的，他因其工作获得了
菲尔兹奖 。 Margulis完整地描述了如果只允许严格的变换，可以使用这些较高阶的格子来变换什么样的空间。
齐默尔的假设成为玛格丽丝作品的自然延续。 它以一列可以在其上工作的最高空间的列表开头-Margulis发现了此列表-并询问此列表是否在扩展，如果允许这些格进行不严格的转换。
在新作品中，三位数学家证明，削弱对称性的定义不会改变高阶晶格的对称性范围。 即使允许晶格进行非常不规则的转换（例如移动，弯曲，拉伸），这些晶格在范围上仍然有严格的限制。
“当然，在为问题陈述增加这种灵活性之后，显然，网格可以发挥更大的作用。 因此，令人惊讶的是，实际上答案是“不”，在某些情况下他们不能。
数学家已经建立了空间尺寸与晶格尺寸或等级之间的精确对应关系，因为在给定空间中可以发挥对称作用的晶格。 通常，他们表明晶格的等级越高，可以容纳晶格的空间就需要进行更多的测量。 即使在转换空间方面具有相当大的灵活性，高级格的转换也仅限于更高的尺寸。
威尔金森说：“这表明空间结构中存在一些非常基本的东西，这意味着它们能够适应这种转变。”
Zimmer的假设只是大型程序的第一步。 经过处理，该作品的合著者对可以转换高级格子的空间施加了严格的限制。 作品的下一个更雄心勃勃的阶段是将精力集中在可以存在格子的那些空间上，然后对这些格子的所有不同转换方式进行分类。
“最后，程序应该能够对所有这些方法进行分类。 齐默说：“除了简单地确定格栅在某些地方无法运行的事实之外，还有许多有趣的问题。”