🏪 🚷 📠 朱莉娅和动力系统的相像 ⏹️ ✉️ 👨🏾‍🎨

我们将继续掌握年轻而有前途的通用语言Julia 。但是对于初学者来说，我们确实需要非常狭窄的应用可能性-解决物理上的典型问题。这是掌握该乐器最方便的策略：为了获得帮助，我们将解决紧迫的问题，逐步增加复杂性，并找到使我们的生活更轻松的方法。简而言之，我们将解决差异和构建图。

首先，请下载Gadfly图形包，然后立即下载完整版的开发人员，以使其与我们的Julia 1.0.1兼容。我们使用REPL，JUNO或Jupyter笔记本电脑驾驶：

using Pkg pkg"add Compose#master" pkg"add Gadfly#master"

不是最方便的选择，但是在等待PlotlyJS更新时，可以尝试进行比较。

您还需要一个功能强大的工具来求解微分方程。

 ]add DifferentialEquations #

这是最广泛且受支持的软件包，提供了许多解决差异的方法。现在进入相图。

常微分方程的解通常更方便以异常形式表示 $y ^ 1（t），...，y ^ L（t）$ ，并沿着相空间绘制每个找到的函数的值。此外，参数t仅在参数上包含在图中。在两个ODE的情况下，这种图形-系统的相图-是相平面上的曲线，因此尤其明显。

振荡器

谐波振荡器动力学 $\伽玛$ 由以下方程组描述：

点 点 伽 马

$\点{x} = y \\ \点{y} =-\ omega ^ 2x + \伽马y$

并且不管初始条件（x0，y0），它都处于平衡状态，即偏转角为零且速度为零的点（0,0）。

在 $\伽马= 0$ 该解决方案采用经典振荡器的形式。

 using DifferentialEquations, Gadfly #     -    function garmosc(ω = pi, γ = 0, x0 = 0.1, y0 = 0.1) A = [0 1 -ω^2 γ] syst(u,p,t) = A * u # ODE system u0 = [x0, y0] # start cond-ns tspan = (0.0, 4pi) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, RK4(),reltol=1e-6, timeseries_steps = 4) N = length(sol.u) J = length(sol.u[1]) U = zeros(N, J) for i in 1:N, j in 1:J U[i,j] = sol.u[i][j] #      end U end

让我们分析一下代码。该功能接受频率和衰减参数以及初始条件的值。嵌套的syst（）函数定义系统。为了证明这一点，他们使用了单行矩阵乘法。带有大量参数的Solve（）函数可灵活配置以解决问题，但我们仅指出了解决方法-Runge-Kutta 4（还有许多其他方法），相对误差以及并非所有点都应保存的事实，但每四分之一应保存。响应矩阵存储在变量sol中 ，此外， sol.t包含时间向量，而sol.u在这些时间求解系统。所有这些都在Plots中平静地绘制，对于Gadfly，您必须更方便地在矩阵中完成答案。我们不需要时间，所以我们只返回解决方案。

让我们建立一个相像：

 Ans0 = garmosc() plot(x = Ans0[:,1], y = Ans0[:,2])

在高阶函数中， broadcast(f, [1, 2, 3])对我们来说尤其值得注意，它交替将数组[1、2、3]的值替换为函数f 。短记录f.([1, 2, 3]) 。这对于更改频率，衰减参数，初始坐标和初始速度很有用。

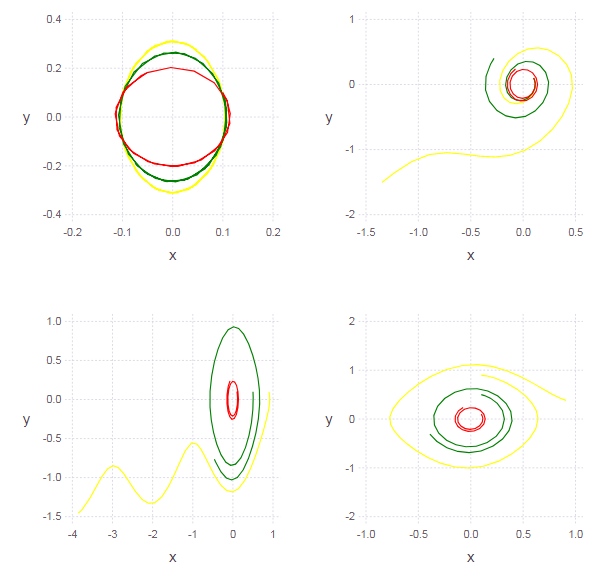
隐藏在扰流板下

 L = Array{Any}(undef, 3)#     (  ) clr = ["red" "green" "yellow"] function ploter(Answ) for i = 1:3 L[i] = layer(x = Answ[i][:,1], y = Answ[i][:,2], Geom.path, Theme(default_color=clr[i]) ) end p = plot(L[1], L[2], L[3]) end Ans1 = garmosc.( [pi 2pi 3pi] )#  p1 = ploter(Ans1) Ans2 = garmosc.( pi, [0.1 0.3 0.5] )#  p2 = ploter(Ans2) Ans3 = garmosc.( pi, 0.1, [0.2 0.5 0.8] ) p3 = ploter(Ans3) Ans4 = garmosc.( pi, 0.1, 0.1, [0.2 0.5 0.8] ) p4 = ploter(Ans4) set_default_plot_size(16cm, 16cm) vstack( hstack(p1,p2), hstack(p3,p4) ) #

现在我们考虑的不是小振荡，而是任意幅度的振荡：

点 点 （ ）

$\点{x} = y \\ \点{y} =-sin（\ omega x）+ \ gamma y$

解决方案的相位图不是椭圆形（它表示振荡器的非线性）。我们选择的振荡幅度（即初始条件）越少，非线性的出现就越少（因此，摆的小振荡可被视为谐波）。

隐藏在扰流板下

 function ungarmosc(ω = pi, γ = 0, x0 = 0.1, y0 = 0.1) function syst(du,u,p,t) du[1] = u[2] du[2] = -sin( ω*u[1] )+γ*u[2] end u0 = [x0, y0] # start cond-ns tspan = (0.0, 2pi) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, RK4(),reltol=1e-6, timeseries_steps = 4) N = length(sol.u) J = length(sol.u[1]) U = zeros(N, J) for i in 1:N, j in 1:J U[i,j] = sol.u[i][j] #      end U end Ans1 = ungarmosc.( [pi 2pi 3pi] ) p1 = ploter(Ans1) Ans2 = ungarmosc.( pi, [0.1 0.4 0.7] ) p2 = ploter(Ans2) Ans3 = ungarmosc.( pi, 0.1, [0.1 0.5 0.9] ) p3 = ploter(Ans3) Ans4 = ungarmosc.( pi, 0.1, 0.1, [0.1 0.5 0.9] ) p4 = ploter(Ans4) vstack( hstack(p1,p2), hstack(p3,p4) )

布鲁塞尔

该模型描述了其中扩散起作用的某种自催化化学反应。该模型于1968年由Lefebvre和Prigozhin提出。

点 （ ） 点

$\点{u} _1 =-（\ mu + 1）u_1 + u ^ 2_1u_2 + 1 \\ \点{u} _2 = \ mu u_1-u ^ 2_1u_2$

未知功能 $u_1（t），\，u_2（t）$ 反映化学反应中间产物浓度的动态变化。型号参数 $\亩$ 催化剂（第三种物质）的初始浓度是合理的。

更详细地讲，可通过对各种参数进行计算来观察布鲁塞尔的相位图的演变。 $\亩$ 。随着其增加，节点将首先逐渐移至坐标为（1， $\亩$ ），直到达到分叉值 $\亩$ = 2。在这一点上，肖像画发生了质的变化，以极限循环的形式表达出来。随着进一步增加 $\亩$ 该循环的参数仅发生定量变化。

隐藏在扰流板下

 function brusselator(μ = 0.1, u0 = [0.1; 0.1]) function syst(du,u,p,t) du[1] = -(μ+1)*u[1] + u[1]*u[1]*u[2] + 1 du[2] = μ*u[1] - u[1]*u[1]*u[2] end tspan = (0.0, 10) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, RK4(),reltol=1e-6, timeseries_steps = 1) N = length(sol.u) J = length(sol.u[1]) U = zeros(N, J) for i in 1:N, j in 1:J U[i,j] = sol.u[i][j] #      end U end L = Array{Any}(undef, 10) function ploter(Answ) for i = 1:length(Answ) L[i] = layer(x = Answ[i][:,1], y = Answ[i][:,2], Geom.path ) end plot(L[1], L[2], L[3], L[4], L[5], L[6], L[7], L[8], L[9], L[10]) end SC = [ [0 0.5], [0 1.5], [2.5 0], [1.5 0], [0.5 1], [1 0], [1 1], [1.5 2], [0.1 0.1], [0.5 0.2] ] Ans1 = brusselator.( 0.1, SC ) Ans2 = brusselator.( 0.8, SC ) Ans3 = brusselator.( 1.6, SC ) Ans4 = brusselator.( 2.5, SC ) p1 = ploter(Ans1) p2 = ploter(Ans2) p3 = ploter(Ans3) p4 = ploter(Ans4) set_default_plot_size(16cm, 16cm) vstack( hstack(p1,p2), hstack(p3,p4) )

今天足够了。下次，我们将尝试学习如何将另一个图形包用于新任务，同时在Julia的语法上键入我们的手。在解决问题的过程中，慢慢地可以追溯到它们的踪影，而不是优点和缺点是简单明了的……而是便利和不便之处–应该为此单独进行讨论。而且，当然，我希望我的哈勃作品比带功能的游戏更严肃-因此，我敦促法官向更多的人介绍更严肃的项目，这将帮助很多人，尤其是在学习这种奇妙的语言方面。

朱莉娅和动力系统的相像

振荡器

布鲁塞尔

More articles: