💗 🤜🏾 ⬜️ 朱莉娅和偏微分方程 ✊🏼 🍈 🚶🏻

以典型的物理模型为例，我们将巩固使用函数的技巧，并熟悉快速，方便且美观的PyPlot可视化工具，该工具提供了Python Matplotlib的所有功能。会有很多照片（隐藏在扰流板下）

我们确保一切都干净，新鲜：

引擎盖下

]status Status `C:\Users\\.julia\environments\v1.0\Project.toml` [537997a7] AbstractPlotting v0.9.0 [ad839575] Blink v0.8.1 [159f3aea] Cairo v0.5.6 [5ae59095] Colors v0.9.5 [8f4d0f93] Conda v1.1.1 [0c46a032] DifferentialEquations v5.3.1 [a1bb12fb] Electron v0.3.0 [5789e2e9] FileIO v1.0.2 [5752ebe1] GMT v0.5.0 [28b8d3ca] GR v0.35.0 [c91e804a] Gadfly v1.0.0+ #master (https://github.com/GiovineItalia/Gadfly.jl.git) [4c0ca9eb] Gtk v0.16.4 [a1b4810d] Hexagons v0.2.0 [7073ff75] IJulia v1.13.0+ [`C:\Users\\.julia\dev\IJulia`] [6218d12a] ImageMagick v0.7.1 [c601a237] Interact v0.9.0 [b964fa9f] LaTeXStrings v1.0.3 [ee78f7c6] Makie v0.9.0+ #master (https://github.com/JuliaPlots/Makie.jl.git) [7269a6da] MeshIO v0.3.1 [47be7bcc] ORCA v0.2.0 [58dd65bb] Plotly v0.2.0 [f0f68f2c] PlotlyJS v0.12.0+ #master (https://github.com/sglyon/PlotlyJS.jl.git) [91a5bcdd] Plots v0.21.0 [438e738f] PyCall v1.18.5 [d330b81b] PyPlot v2.6.3 [c4c386cf] Rsvg v0.2.2 [60ddc479] StatPlots v0.8.1 [b8865327] UnicodePlots v0.3.1 [0f1e0344] WebIO v0.4.2 [c2297ded] ZMQ v1.0.0

否则，我们将获得今天所需的一切

 julia>] pkg> add PyCall pkg> add LaTeXStrings pkg> add PyPlot pkg> build PyPlot #     build #    -      ,    pkg> add Conda #    Jupyter -    pkg> add IJulia #      pkg> build IJulia #     build

现在开始任务！

进位方程

在物理学中，术语“转移”应理解为是指不可逆的过程，其结果是在物理系统中发生了质量，动量，能量，电荷或某些其他物理量的空间运动（转移）。
线性一维输运方程（或对流方程）-最简单的偏微分方程-表示为

f r a c \部 分 U （ x ， t ） \部 分 t + c f r a c \部 分 U （ x ， t ） \部 分 x = P h i （ U ， x ， t ）

$\ frac {\部分U（x，t）} {\部分t} + c \ frac {\部分U（x，t）} {\部分x} = \ Phi（U，x，t）$

对于运输方程的数值解，可以使用显式差分方案：

f r a c h a t U_{i} - U_{i} t a u + c f r a c U_{i} - U_{i - 1} D e l t a = f r a c P h i_{i - 1} + P h i_{i} 2 美

$\ frac {\ hat {U} _i-U_i} {\ tau} + c \ frac {U_i-U_ {i-1}} {\ Delta} = \ frac {\ Phi_ {i-1} + \ Phi_i} {2}美$

在哪里 $\帽子{U}$ -较高时间层上的网格函数的值。该电路的Courant编号稳定。 $K = c \ tau / \ Delta <1$

非线性转移

f r a c \部 分 U （ x ， t ） \部 分 t + （ C_{0} + U C_{1} ） f r a c \部 分 U （ x ， t ） \部 分 x = P h i （ U ， x ， t ）

$\ frac {\部分U（x，t）} {\部分t} +（C_0 + UC_1）\ frac {\部分U（x，t）} {\部分x} = \ Phi（U，x，t ）$

线源（吸收转移）： $\ Phi（U，x，t）=-BU$ 。我们使用显式差异方案：

U_{i}^{j + 1} = \左 （ 1 - f r a c h_{t} B 2 - f r a c h_{t} C_{0} h_{x} - f r a c h_{t} C_{1} h_{x} U_{i}^{j} r i g h t ） U_{i}^{j} + U_{i - 1}^{j} \左 （ f r a c h_{t} C_{0} h_{x} - f r a c h_{t} B 2 + f r a c h_{t} C_{1} h_{x} U_{i}^{j} r i g h t ）

$U ^ {j + 1} _i = \左（1- \ frac {h_tB} {2}-\ frac {h_tC_0} {h_x}-\ frac {h_tC_1} {h_x} U ^ j_i \ right）U ^ j_i + U ^ j_ {i-1} \左（\ frac {h_tC_0} {h_x}-\ frac {h_tB} {2} + \ frac {h_tC_1} {h_x} U ^ j_i \ right）$

 using Plots pyplot() a = 0.2 b = 0.01 ust = x -> x^2 * exp( -(xa)^2/b ) #   bord = t -> 0. #  #    - function transferequi(;C0 = 1., C1 = 0., B = 0., Nx = 50, Nt = 50, tlmt = 0.01) dx = 1/Nx dt = tlmt/Nt b0 = 0.5B*dt c0 = C0*dt/dx c1 = C1*dt/dx print("Kurant: $c0 $c1") x = [i for i in range(0, length = Nx, step = dx)]#         t = [i for i in range(0, length = Nt, step = dt)] #   -   U = zeros(Nx, Nt) U[:,1] = ust.(x) U[1,:] = bord.(t) for j = 1:Nt-1, i = 2:Nx U[i, j+1] = ( 1-b0-c0-c1*U[i,j] )*U[i,j] + ( c0-b0+c1*U[i,j] )*U[i-1,j] end t, x, U end t, X, Ans0 = transferequi( C0 = 4., C1 = 1., B = 1.5, tlmt = 0.2 ) plot(X, Ans0[:,1], lab = "t1") plot!(X, Ans0[:,10], lab = "t10") p = plot!(X, Ans0[:,40], lab = "t40") plot( p, heatmap(t, X, Ans0) ) #

结果

让我们增加吸收：

 t, X, Ans0 = transferequi( C0 = 2., C1 = 1., B = 3.5, tlmt = 0.2 ) plot(X, Ans0[:,1]) plot!(X, Ans0[:,10]) p = plot!(X, Ans0[:,40]) plot( p, heatmap(t, X, Ans0) )

结果

 t, X, Ans0 = transferequi( C0 = 1., C1 = 15., B = 0.1, Nx = 100, Nt = 100, tlmt = 0.4 ) plot(X, Ans0[:,1]) plot!(X, Ans0[:,20]) plot!(X, Ans0[:,90])

差点撞倒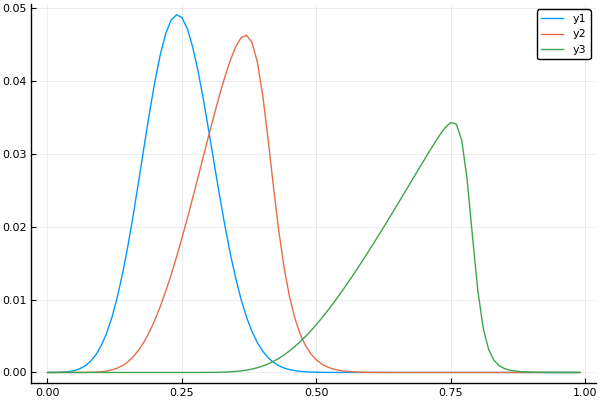

heatmap(t, X, Ans0)

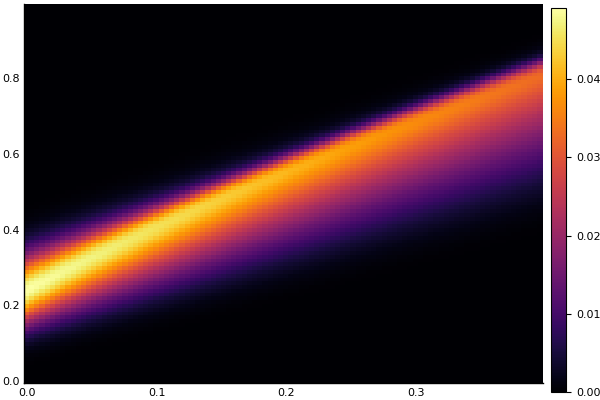
热方程

差分热方程（或热扩散方程）的写法如下：

f r a c \部 分 T （ x ， t ） \部 分 t + D f r a c \部 分^{2} U （ x ， t ） \部 分 x^{2} = p h i （ T ， x ， t ）

$\ frac {\部分T（x，t）} {\部分t} + D \ frac {\部分^ 2 U（x，t）} {\部分x ^ 2} = \ phi（T，x，t ）$

这是一个抛物线方程，包含关于时间t的一阶导数和关于空间坐标x的第二阶。它描述了例如冷却或加热金属棒的温度动态变化（函数T描述了沿着金属棒的x坐标的温度曲线）。系数D被称为导热系数（扩散）。它可以是常数，也可以是常数，既取决于坐标，又取决于所需的函数D（t，x，T）本身。

考虑线性方程（扩散系数和热源与温度无关）。分别使用显式和隐式Euler方案的微分方程的差分近似：

f r a c T_{i ， n + 1} - T_{i ， n} t a u = D f r a c T_{i - 1 ， n} - 2 T_{i ， n} + T_{i + 1 ， n} D e l t a^{2} + p h i_{i ， n} f r a c T_{i ， n + 1} - T_{i ， n} t a u = D f r a c T_{i - 1 ， n + 1} - 2 T_{i ， n + 1} + T_{i + 1 ， n + 1} D e l t a^{2} + p h i_{i ， n}

$\ frac {T_ {i，n + 1} -T_ {i，n}} {\ tau} = D \ frac {T_ {i-1，n} -2T_ {i，n} + T_ {i + 1 ，n}} {\ Delta ^ 2} + \ phi_ {i，n} \\ \ frac {T_ {i，n + 1} -T_ {i，n}} {\ tau} = D \ frac {T_ { i-1，n + 1} -2T_ {i，n + 1} + T_ {i + 1，n + 1}} {\ Delta ^ 2} + \ phi_ {i，n}$

 δ(x) = x==0 ? 0.5 : x>0 ? 1 : 0 # -     startcond = x-> δ(x-0.45) - δ(x-0.55) #   bordrcond = x-> 0. #    D(u) = 1 #   Φ(u) = 0 #    #      LaTex    Tab # \delta press Tab -> δ function linexplicit(Nx = 50, Nt = 40; tlmt = 0.01) dx = 1/Nx dt = tlmt/Nt k = dt/(dx*dx) print("Kurant: $k dx = $dx dt = $dt k<0.5? $(k<0.5)") x = [i for i in range(0, length = Nx, step = dx)] #         t = [i for i in range(0, length = Nt, step = dt)] #   -   U = zeros(Nx, Nt) U[: ,1] = startcond.(x) U[1 ,:] = U[Nt,:] = bordrcond.(t) for j = 1:Nt-1, i = 2:Nx-1 U[i, j+1] = U[i,j]*(1-2k*D( U[i,j] )) + k*U[i-1,j]*D( U[i-1,j] ) + k*U[i+1,j]*D( U[i+1,j] ) + dt*Φ(U[i,j]) end t, x, U end t, X, Ans2 = linexplicit( tlmt = 0.005 ) plot(X, Ans2[:,1], lab = "t1") plot!(X, Ans2[:,10], lab = "t10") p = plot!(X, Ans2[:,40], lab = "t40", title = "Explicit scheme") plot( p, heatmap(t, X, Ans2) )

结果

我们使用隐式方案和扫描方法

 function nonexplicit(Nx = 50, Nt = 40; tlmt = 0.01) dx = 1/Nx dt = tlmt/Nt k = dt/(dx*dx) print("Kurant: $k dx = $dx dt = $dt k<0.5? $(k<0.5)\n") x = [i for i in range(0, length = Nx, step = dx)] t = [i for i in range(0, length = Nt, step = dt)] U = zeros(Nx, Nt) η = zeros(Nx+1) ξ = zeros(Nx) U[: ,1] = startcond.(x) U[1 ,:] = bordrcond.(t) U[Nt,:] = bordrcond.(t) for j = 1:Nt-1 b = -1 - 2k*D( U[1,j] ) c = -k*D( U[2,j] ) d = U[1,j] + dt*Φ(U[1,j]) ξ[2] = c/b η[2] = -d/b for i = 2:Nx-1 a = -k*D( U[i-1,j] ) b = -2k*D( U[i,j] ) - 1 c = -k*D( U[i+1,j] ) d = U[i,j] + dt*Φ(U[i,j]) ξ[i+1] = c / (ba*ξ[i]) η[i+1] = (a*η[i]-d) / (ba*ξ[i]) end U[Nx,j+1] = η[Nx] for i = Nx:-1:2 U[i-1,j+1] = ξ[i]*U[i,j+1] + η[i] end end t, x, U end plot(X, Ans2[:,1], lab = "ex_t1") plot!(X, Ans2[:,10], lab = "ex_t10") plot!(X, Ans2[:,40], lab = "ex_t40") plot!(X, Ans3[:,1], lab = "non_t1") plot!(X, Ans3[:,10], lab = "non_t10") plot!(X, Ans3[:,40], lab = "non_t40", title = "Comparison schemes")

电路比较

非线性热方程

对于非线性热方程，例如使用非线性热源，可以获得更多有趣的解决方案 $\ phi（x，T）= 10 ^ 3（T-T ^ 3）$ 。如果以这种形式设置，则会得到热前沿形式的解决方案，并在主加热区的两侧传播

 Φ(u) = 1e3*(uu^3) t, X, Ans4 = linexplicit( tlmt = 0.005 ) plot(X, Ans4[:,1], lab = "ex_t1") plot!(X, Ans4[:,10], lab = "ex_t10") plot!(X, Ans4[:,40], lab = "ex_t40", title = "Thermal front")

热锋面

随着扩散系数的非线性，甚至可能会有更多意想不到的解决方案。例如，如果您采取 $D（x，T）= T ^ 2$ ， $\ phi（x，T）= 10 ^ 3T ^ {3.5}$ ，然后可以观察到介质燃烧的效果，该介质位于其主要加热区域（“加重燃烧” S模式）。
同时，我们将检查隐式方案如何在源和扩散系数均为非线性的情况下工作

 D(u) = u*u Φ(u) = 1e3*abs(u)^(3.5) t, X, Ans5 = linexplicit( tlmt = 0.0005 ) t, X, Ans6 = nonexplicit( tlmt = 0.0005 ) plot(X, Ans5[:,1], lab = "ex_t1") plot!(X, Ans5[:,10], lab = "ex_t10") p1 = plot!(X, Ans5[:,40], lab = "ex_t40", title = "Burning with aggravation") p2 = heatmap(abs.(Ans6-Ans5), title = "Difference") #      plot(p1, p2)

S模式

波动方程

双曲波方程

f r a c \部 分^{2} U （ x ， t ） \部 分 t^{2} = c^{2} f r a c \部 分^{2} U （ x ， t ） \部 分 x^{2}

$\ frac {\部分^ 2 U（x，t）} {\部分t ^ 2} = c ^ 2 \ frac {\部分^ 2 U（x，t）} {\部分x ^ 2}$

描述没有分散的一维线性波。例如，弦的振动，液体（气体）中的声音或真空中的电磁波（在后一种情况下，等式应以矢量形式编写）。

逼近该方程的最简单差分方案是显式五点方案

f r a c U_{i}^{n + 1} - 2 U_{i}^{n} + U_{i}^{n - 1} t a u^{2} = c^{2} f r a c U_{i + 1}^{n} - 2 U_{i}^{n} + U_{i - 1}^{n} h^{2} x_{i} = i h ， \， t_{n} = t a u

$\ frac {U ^ {n + 1} _i-2U ^ {n} _i + U ^ {n-1} _i} {\ tau ^ 2} = c ^ 2 \ frac {U ^ n_ {i + 1} -2U ^ n_i + U ^ n_ {i-1}} {h ^ 2} \\ x_i = ih，\，t_n = \ tau$

该方案称为“交叉”，在时间和空间坐标上具有第二级精度，并且在时间上为三层。

 #     ψ = x -> x^2 * exp( -(x-0.5)^2/0.01 ) #    ϕ(x) = 0 c = x -> 1 #     function pdesolver(N = 100, K = 100, L = 2pi, T = 10, a = 0.1 ) dx = L/N; dt = T/K; gam(x) = c(x)*c(x)*a*a*dt*dt/dx/dx; print("Kurant-Fridrihs-Levi: $(dt*a/dx) dx = $dx dt = $dt") u = zeros(N,K); x = [i for i in range(0, length = N, step = dx)] #      u[:,1] = ψ.(x); u[:,2] = u[:,1] + dt*ψ.(x); #     fill!( u[1,:], 0); fill!( u[N,:], ϕ(L) ); for t = 2:K-1, i = 2:N-1 u[i,t+1] = -u[i,t-1] + gam( x[i] )* (u[i-1,t] + u[i+1,t]) + (2-2*gam( x[i] ) )*u[i,t]; end x, u end N = 50; #     K = 40; #    a = 0.1; #    L = 1; #   T = 1; #   t = [i for i in range(0, length = K, stop = T)] X, U = pdesolver(N, K, L, T, a) #    plot(X, U[:,1]) plot!(X, U[:,40])

结果

要构建表面，我们将直接使用PyPlot作为Plots环境。

表面图

 using PyPlot surf(t, X, U)

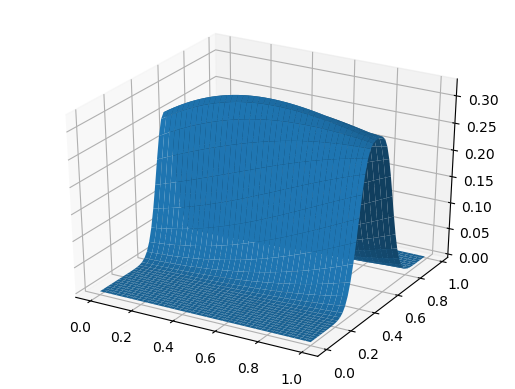
对于甜点，波的传播速度取决于坐标：

 ψ = x -> x>1/3 ? 0 : sin(3pi*x)^2 c = x -> x>0.5 ? 0.5 : 1 X, U = pdesolver(400, 400, 8, 1.5, 1) plot(X, U[:,1]) plot!(X, U[:,40]) plot!(X, U[:,90]) plot!(X, U[:,200], xaxis=("  ", (0, 1.5), 0:0.5:2) )

结果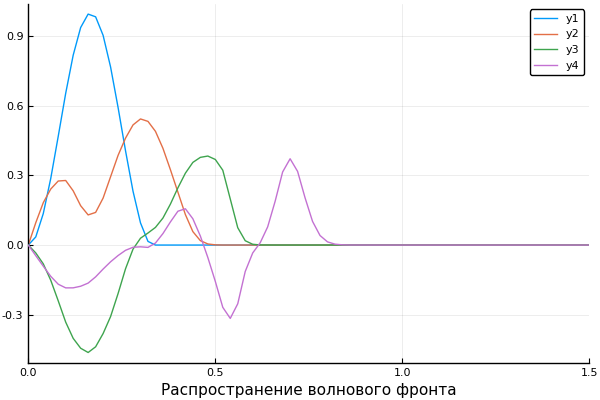

 U2 = [ U[i,j] for i = 1:60, j = 1:size(U,2) ] #    surf(U2) #

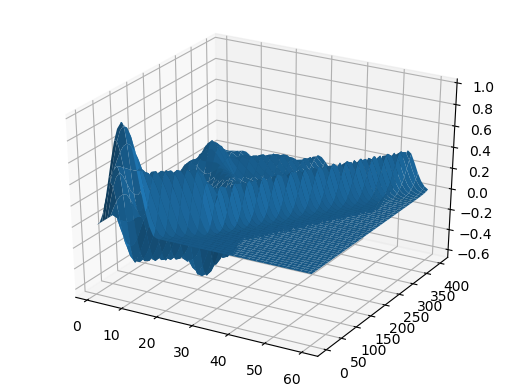
heatmap(U, yaxis=(" ", (0, 50), 0:10:50))

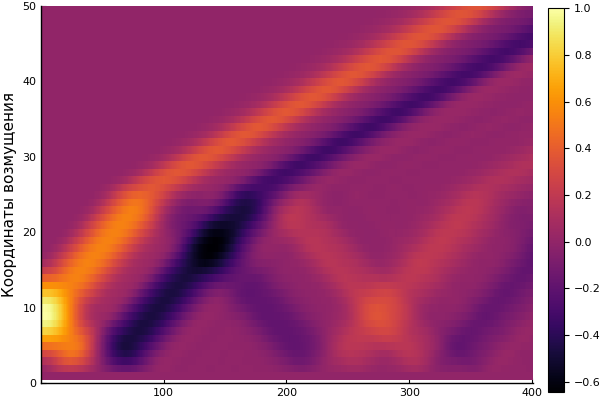
今天足够了。如需更详细的评论：
指向github的PyPlot链接，用作环境的Plot的其他示例，以及Julia 编写的不错的俄语备忘录。

朱莉娅和偏微分方程

进位方程

非线性转移

热方程

非线性热方程

波动方程

More articles: