可变自动编码器（auto-encoder）是一种生成模型，可以学习在给定的隐藏空间中显示对象。

有没有想过变分自动编码器（VAE）模型如何工作？ 是否想知道VAE如何生成新示例，例如对其进行训练的数据集？ 阅读本文后，您将对VAE的内部运作有一个理论上的了解，也可以自己实现。 然后，我将展示在一组手写数字上训练的有效VAE代码，我们将获得一些乐趣，生成新的数字！

生成模型

VAE是一个生成模型-它估计训练数据的概率密度（PDF）。 如果以自然图像训练这种模型，则它将为狮子图像分配高概率值，为随机胡话图像分配低值。

VAE模型还能够从经过培训的PDF中获取示例，这是最酷的部分，因为它可以生成类似于原始数据集的新示例！

我将使用手写数字集MNIST来解释VAE。 模型的输入数据是格式为图片的图片 $$$\ mathbb {R} ^ {28×28}$。 模型应评估输入看起来像数字的可能性。

图像建模任务

像素之间的交互是一项艰巨的任务。 如果像素彼此独立，则需要独立研究每个像素的PDF，这很容易。 选择也很简单-我们将每个像素分开。

但是在数字图像中，像素之间存在明显的依存关系。 如果您在左半部分看到四个数字的开头，那么如果右半部分是零的补全，您会感到非常惊讶。 但是为什么呢？

隐藏的空间

您知道每个图像都有一个数字。 进入 $$$\ mathbb {R} ^ {28×28}$显然不包含此信息。 但是它必须在某个地方。这个“某处”是一个隐藏的空间。



您可以将隐藏空间视为 $$$\ mathbb {R} ^ {k}$每个向量包含 $$$k$渲染图像所需的一些信息。 假设第一维包含一个由数字表示的数字。 第二尺寸可以是宽度。 第三个是角度，依此类推。

我们可以想象分两个步骤画一个人的过程。 首先，一个人有意或无意地确定了将要显示的数字的所有属性。 接下来，将这些决定转化为笔触。

VAE正在尝试模拟此过程：对于给定的图像 $$$x$我们希望找到至少一个可以描述它的隐藏矢量； 一个包含生成指令的向量 $$$x$。 用总概率公式来表示 ，我们得到 $$$P（x）= \ int P（x | z）P（z）dz$。

让我们对这个方程式有一些合理的理解：

• 整体性意味着必须在所有隐藏空间中寻找候选人。
• 对于每个候选人 $$$z$我们问一个问题：是否有可能产生 $$$x$使用说明 $$$z$？ 够大吗 $$$P（x | z）$？ 例如，如果 $$$z$编码有关数字7的信息，则图像8是不可能的。 但是，图像1是可以接受的，因为1和7相似。
• 我们找到了一个好人。 $$$z$？ 太好了！ 但是请稍等...多少钱 $$$z$大概吧 $$$P（z）$足够大吗？ 考虑倒数7的图像。理想的匹配是描述视图7的隐藏矢量，其中角度大小设置为180°。 但是这样 $$$z$不太可能，因为通常数字不是以180°的角度书写的。

VAE培训的目标是最大限度地提高 $$$P（x）$。 我们将建模 $$$P（x | z）$使用多维高斯分布 $$$\数学{N}（f（z），\ sigma ^ 2 \ cdot I）$。

$$$f（z）$使用神经网络建模。 $$$\ sigma$是用于乘以单位矩阵的超参数 $$$我$。

请记住 $$$f$-这就是我们将使用经过训练的模型生成新图像的方法。 重叠高斯分布仅用于教育目的。 如果我们采用Dirac delta函数（即确定性 $$$x = f（z）$），那么我们将无法使用梯度下降训练模型！

隐藏空间的奇观

隐藏空间方法有两个大问题：

1. 每个维度包含哪些信息？ 一些尺寸可能与抽象元素有关，例如样式。 即使很容易解释所有维度，我们也不想为数据集分配标签。 这种方法无法扩展到其他数据集。
2. 当尺寸之间存在相关性时，隐藏的空间可能会造成混淆。 例如，一个非常快速绘制的数字可能同时导致出现斜角和较细的笔触。 定义这些依赖关系很困难。

深度学习助您一臂之力

事实证明，可以通过将相当复杂的函数应用于标准多维高斯分布来生成每个分布。

选择 $$$P（z）$作为标准的多维高斯分布。 通过神经网络进行建模 $$$f$可以分为两个阶段：

1. 第一层将高斯分布映射到隐藏空间上的真实分布。 我们无法解释测量值，但这无关紧要。
2. 随后的图层将从隐藏空间中显示 $$$P（x | z）$。

那么我们如何训练这种野兽呢？

公式 $$$P（x）$不溶的，因此，我们通过蒙特卡洛方法对其进行近似：

1. 选拔 $$$\ {z_i \} _ {i = 1} ^ n$ 从以前的 $$$P（z）$
2. 与近似 $$$P（x）\大约\ frac {1} {n} \ sum_ {i = 1} ^ n P（x | z_i）$

太好了！ 因此，尝试很多不同的方法 $$$z$并启动错误传播派对！

不幸的是 $$$x$要获得一个合理的近似值，需要非常多的多维数据。 我的意思是如果你尝试 $$$z$，那么获得看起来像的图像的机会是什么 $$$x$？ 顺便说一下，这解释了为什么 $$$P（x | z）$必须为任何可能的图像分配正概率值，否则该模型将无法学习：采样 $$$z$会产生几乎可以肯定与 $$$x$，并且如果概率为0，则渐变将无法传播。

如何解决这个问题？

开路！

大多数样品 $$$z$从选择中不会添加任何内容 $$$P（x）$-他们太过边界了。 现在，如果您提前知道从何处带走……

可以输入 $$$Q（z | x）$。 给定 $$$Q$将被训练为您分配高概率值 $$$z$可能会产生 $$$x$。 现在，您可以使用蒙特卡洛方法进行评估，从 $$$Q$。

不幸的是，出现了一个新问题！ 而不是最大化 $$$P（x）= \ int P（x | z）P（z）dz = \ mathbb {E} _ {z \ sim P（z）} P（x | z）$我们最大化 $$$\ mathbb {E} _ {z \ sim Q（z | x）} P（x | z）$。 它们如何相互关联？

变式结论

变式结论是另一篇文章的主题，因此在此不再详细介绍。 我只能说这些分布与以下等式相关：

$$

$$log P（X）-\ mathcal {KL} [Q（z | x）|| P（z | x）] = \ mathbb {E} _ {z \ sim Q（z | x）} [log P（x | z）]-\ mathcal {KL} [Q（z | x）|| P（z）]$$

$$$\ mathcal {KL}$是Kullback – Leibler距离 ，它直观地评估了两个分布的相似性。

稍后，您将看到如何最大化方程式的右侧。 在这种情况下，左侧也会最大化：

• $$$P（x）$最大化。
• 多远 $$$Q（z | x）$来自 $$$P（z | x）$- 真正的先验未知-将被最小化。

等式右边的意思是我们在这里有张力：

1. 一方面，我们要最大限度地提高 $$$x$必须从 $$$z \ sim Q$。
2. 另一方面，我们想要 $$$Q（z | x）$（ 编码器 ）与之前的类似 $$$P（z）$（多维高斯分布）。 这可以看作是正则化。

差异最小化 $$$\ mathcal {KL}$正确选择发行版即可轻松执行。 我们将模拟 $$$Q（z | x）$作为神经网络，其输出是多维高斯分布的参数：

• 平均 $$$\ mu_Q$
• 对角协方差矩阵 $$$\ Sigma_Q$

然后发散 $$$\ mathcal {KL}$变得可解析地求解，这对我们（和梯度）都非常有用。

解码器部分要复杂一些。 乍一看，我想指出的是，蒙特卡罗方法无法解决这个问题。 但是样品 $$$z$来自 $$$Q$将不允许渐变传播通过 $$$Q$，因为选择不是微分运算。 这是一个问题，因为从那以后发布层的权重 $$$\ Sigma_Q$和 $$$\ mu_Q$。

新的参数设置技巧

我们可以更换 $$$Q$非参数随机变量的确定性参数化转换：

1. 来自标准（无参数）高斯分布的样本。
2. 将样本乘以平方根 $$$\ Sigma_Q$。
3. 添加到结果 $$$\ mu_Q$。

结果，我们得到的分布等于 $$$Q$。 现在，提取操作来自标准的高斯分布。 因此，梯度可以传播通过 $$$\ Sigma_Q$和 $$$\ mu_Q$从现在开始，这些都是确定性路径。

结果呢 该模型将能够学习如何调整参数 $$$Q$：她将专注于善 $$$z$有能力生产 $$$x$。

全部放在一起

VAE模型可能很难理解。 我们在这里检查了许多难以消化的材料。

让我总结一下实施VAE的所有步骤。



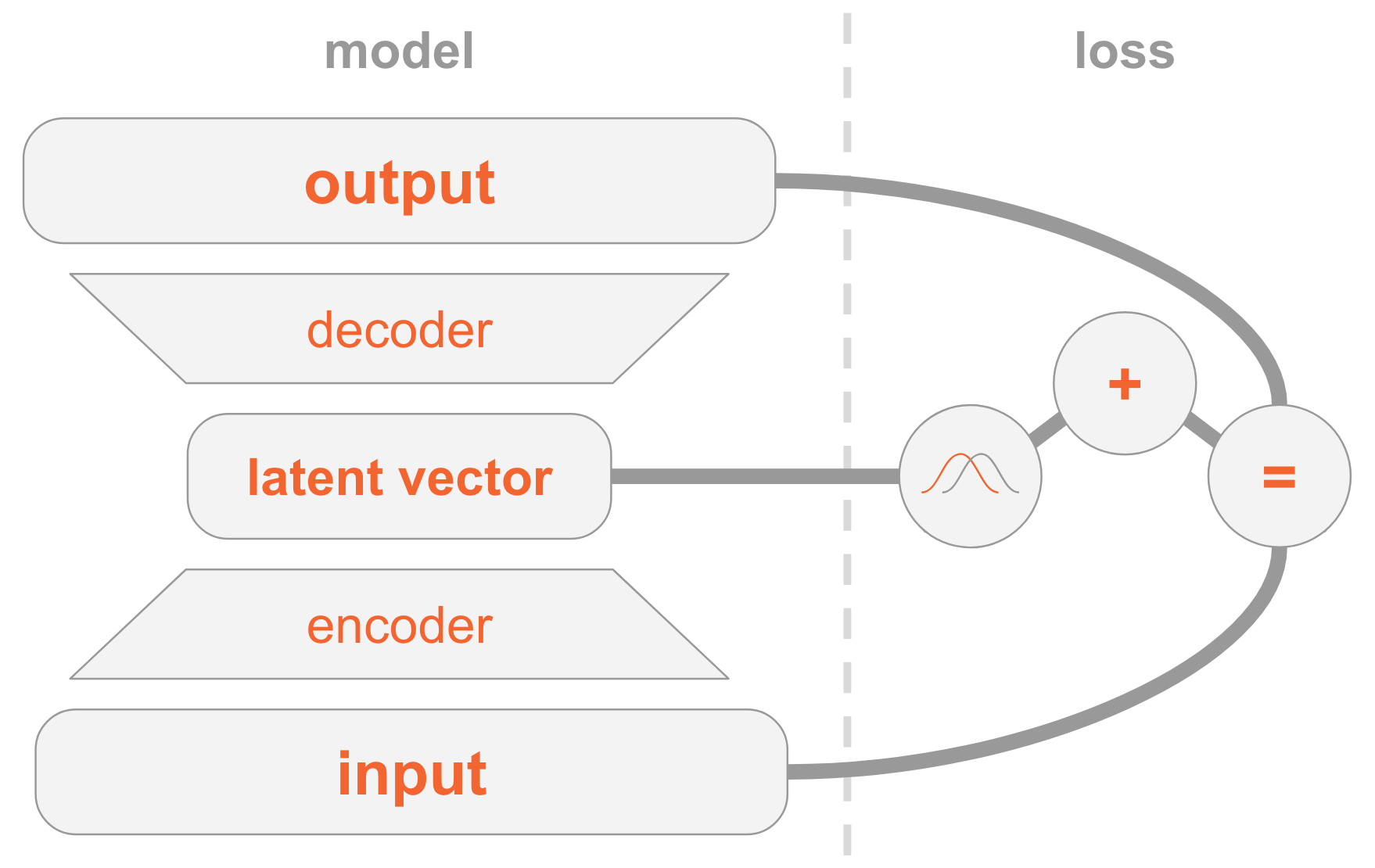
在左侧，我们有一个模型定义：

1. 输入图像通过编码器网络传输。
2. 编码器提供分配参数 $$$Q（z | x）$。
3. 隐藏的向量 $$$z$取自 $$$Q（z | x）$。 如果编码器训练有素，那么在大多数情况下 $$$z$包含说明 $$$x$。
4. 解码器解码 $$$z$进入图像。

在右侧，我们有一个损失函数：

1. 恢复错误：输出应与输入相似。
2. $$$Q（z | x）$应该与前一个相似，即多维标准正态分布。

要创建新图像，您可以直接从先前的发行版中选择隐藏的矢量，并将其解码为图像。

工作代码

现在，我们将更详细地研究VAE，并考虑有效的代码。 您将了解实施VAE所需的所有技术细节。 另外，我将向您展示一个有趣的技巧：如何为隐藏矢量的某些维分配特殊角色，以便模型开始生成指示数字的图片。

import numpy as np import tensorflow as tf from tensorflow.examples.tutorials.mnist import input_data import matplotlib.pyplot as plt np.random.seed(42) tf.set_random_seed(42) %matplotlib inline 

我想提醒您，模型是在MNIST上训练的-一组手写数字。 输入图像采用以下格式 $$$\ mathbb {R} ^ {28×28}$。

 mnist = input_data.read_data_sets('MNIST_data') input_size = 28 * 28 num_digits = 10 

接下来，我们定义超参数。

随意使用不同的值，以了解它们如何影响模型。

 params = { 'encoder_layers': [128], #       'decoder_layers': [128], #    (CNN ,     ) 'digit_classification_layers': [128], #   ,   'activation': tf.nn.sigmoid, #      'decoder_std': 0.5, #   P(x|z)   'z_dim': 10, #    'digit_classification_weight': 10.0, #   ,   'epochs': 20, 'batch_size': 100, 'learning_rate': 0.001 } 

型号

该模型包含三个子网：

1. 得到 $$$x$（图片），将其编码为分布 $$$Q（z | x）$在隐藏的空间。
2. 得到 $$$z$在隐藏空间（图像的代码表示形式）中，将其解码为相应的图像 $$$f（z）$。
3. 得到 $$$x$并通过与10维图层进行比较来确定数字，其中第i个值包含第i个数字的概率。

前两个子网是纯VAE的基础。

第三个是辅助任务 ，它使用一些隐藏的维度对图像中找到的数字进行编码。 我将解释原因：在前面的讨论中，我们并不关心隐藏空间的每个维度包含哪些信息。 模型可以学习编码对其认为有价值的任何信息。 由于我们熟悉数据集，因此我们知道维的重要性，维包含数字的类型（即其数值）。 现在，我们想通过向她提供此信息来帮助模型。

对于给定类型的数字，我们直接对其进行编码，即，我们使用大小为10的向量。这十个数字与隐藏的向量相关联，因此在将该向量解码为图像时，模型将使用数字信息。

提供直接编码矢量模型的方法有两种：

1. 将其添加为模型的输入。
2. 将其添加为标签，以便模型本身将计算预测：我们将添加另一个预测10维向量的子网，其中损失函数是与预期正向编码向量的交叉熵。

选择第二个选项。 怎么了 好吧，那么在测试时，您可以通过两种方式使用模型：

1. 将图像指定为输入并显示隐藏的矢量。
2. 指定隐藏的矢量作为输入并生成图像。

由于我们要支持第一个选项，因此我们无法为模型输入数字，因为我们不想在测试过程中知道它。 因此，模型必须学会预测。

 def encoder(x, layers): for layer in layers: x = tf.layers.dense(x, layer, activation=params['activation']) mu = tf.layers.dense(x, params['z_dim']) var = 1e-5 + tf.exp(tf.layers.dense(x, params['z_dim'])) return mu, var def decoder(z, layers): for layer in layers: z = tf.layers.dense(z, layer, activation=params['activation']) mu = tf.layers.dense(z, input_size) return tf.nn.sigmoid(mu) def digit_classifier(x, layers): for layer in layers: x = tf.layers.dense(x, layer, activation=params['activation']) logits = tf.layers.dense(x, num_digits) return logits 

 images = tf.placeholder(tf.float32, [None, input_size]) digits = tf.placeholder(tf.int32, [None]) #        encoder_mu, encoder_var = encoder(images, params['encoder_layers']) #     ,  #     eps = tf.random_normal(shape=[tf.shape(images)[0], params['z_dim']], mean=0.0, stddev=1.0) z = encoder_mu + tf.sqrt(encoder_var) * eps # classify the digit digit_logits = digit_classifier(images, params['digit_classification_layers']) digit_prob = tf.nn.softmax(digit_logits) #     ,  #    decoded_images = decoder(tf.concat([z, digit_prob], axis=1), params['decoder_layers']) 

 #    ,    #    loss_reconstruction = -tf.reduce_sum( tf.contrib.distributions.Normal( decoded_images, params['decoder_std'] ).log_prob(images), axis=1 ) #         . #      , #         #  ,  KL-   # ,    loss_prior = -0.5 * tf.reduce_sum( 1 + tf.log(encoder_var) - encoder_mu ** 2 - encoder_var, axis=1 ) loss_auto_encode = tf.reduce_mean( loss_reconstruction + loss_prior, axis=0 ) # digit_classification_weight      , #      loss_digit_classifier = params['digit_classification_weight'] * tf.reduce_mean( tf.nn.sparse_softmax_cross_entropy_with_logits(labels=digits, logits=digit_logits), axis=0 ) loss = loss_auto_encode + loss_digit_classifier train_op = tf.train.AdamOptimizer(params['learning_rate']).minimize(loss) 

培训课程

我们将使用SGD训练一个模型，以优化两个损失函数-VAE和分类。

在每个时期结束时，我们选择隐藏的向量并将其解码为图像，以直观地观察模型的生成能力在各个时期中如何提高。 采样方法如下：

1. 明确设置用于按我们要生成的数字进行分类的尺寸。 例如，如果要创建数字2的图像，则可以设置尺寸 $$$[0010000000]$。
2. 从多维正态分布的其他维度中随机选择。 这些是该时代生成的不同数字的值。 因此，我们了解了在其他维度上编码的内容，例如手写风格。

步骤1的含义是，收敛之后，模型应该能够通过这些测量设置对输入图像中的图形进行分类。 但是，它们也用于解码阶段以创建图像。 也就是说，解码器子网知道：当测量值对应于数字2时，它应生成具有该数字的图片。 因此，如果我们手动将测量值设置为数字2，我们将获得此图的生成图像。

 samples = [] losses_auto_encode = [] losses_digit_classifier = [] with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for epoch in xrange(params['epochs']): for _ in xrange(mnist.train.num_examples / params['batch_size']): batch_images, batch_digits = mnist.train.next_batch(params['batch_size']) sess.run(train_op, feed_dict={images: batch_images, digits: batch_digits}) train_loss_auto_encode, train_loss_digit_classifier = sess.run( [loss_auto_encode, loss_digit_classifier], {images: mnist.train.images, digits: mnist.train.labels}) losses_auto_encode.append(train_loss_auto_encode) losses_digit_classifier.append(train_loss_digit_classifier) sample_z = np.tile(np.random.randn(1, params['z_dim']), reps=[num_digits, 1]) gen_samples = sess.run(decoded_images, feed_dict={z: sample_z, digit_prob: np.eye(num_digits)}) samples.append(gen_samples) 

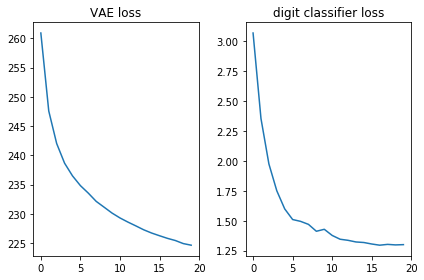
让我们检查两个损失函数是否看起来都不错，即它们是否减少：

 plt.subplot(121) plt.plot(losses_auto_encode) plt.title('VAE loss') plt.subplot(122) plt.plot(losses_digit_classifier) plt.title('digit classifier loss') plt.tight_layout() 

另外，让我们显示生成的图像，看看模型是否真的可以创建带有手写数字的图片：

 def plot_samples(samples): IMAGE_WIDTH = 0.7 plt.figure(figsize=(IMAGE_WIDTH * num_digits, len(samples) * IMAGE_WIDTH)) for epoch, images in enumerate(samples): for digit, image in enumerate(images): plt.subplot(len(samples), num_digits, epoch * num_digits + digit + 1) plt.imshow(image.reshape((28, 28)), cmap='Greys_r') plt.gca().xaxis.set_visible(False) if digit == 0: plt.gca().yaxis.set_ticks([]) plt.ylabel('epoch {}'.format(epoch + 1), verticalalignment='center', horizontalalignment='right', rotation=0, fontsize=14) else: plt.gca().yaxis.set_visible(False) plot_samples(samples) 

结论

很高兴看到一个简单的直接发行网络（没有花哨的卷积）在短短20个时代就产生了精美的图像。 该模型很快学会了对数字使用特殊的度量：在第9个时代，我们已经看到了试图生成的数字序列。

每个纪元对其他维度使用不同的随机值，因此时代之间的风格有所不同，但在时代之间却是相似的：至少在某些时代。 例如，在18号，所有数字都比20号高。

注意事项

本文基于我的经验和以下来源：

• 变异结论与深度学习：新的综合
• 变体自动编码器指南