麻省理工学院的课程“计算机系统安全”。 第16讲：“侧面通道攻击”，第1部分

麻省理工学院。 讲座课程＃6.858。 “计算机系统的安全性。” Nikolai Zeldovich，James Mickens。 2014年

计算机系统安全是一门有关开发和实施安全计算机系统的课程。 讲座涵盖了威胁模型，危害安全性的攻击以及基于最新科学研究的安全技术。 主题包括操作系统（OS）安全性，功能，信息流管理，语言安全性，网络协议，硬件安全性和Web应用程序安全性。

第1课：“简介：威胁模型” 第1 部分 / 第2 部分 / 第3部分
第2课：“控制黑客攻击”， 第1 部分 / 第2 部分 / 第3部分
第3讲：“缓冲区溢出：漏洞利用和保护” 第1 部分 / 第2 部分 / 第3部分
讲座4：“特权分离”， 第1 部分 / 第2 部分 / 第3部分
讲座5：“安全系统从何而来？” 第1 部分 / 第2部分
讲座6：“机会” 第1 部分 / 第2 部分 / 第3部分
讲座7：“本地客户端沙箱” 第1 部分 / 第2 部分 / 第3部分
讲座8：“网络安全模型” 第1 部分 / 第2 部分 / 第3部分
讲座9：“ Web应用程序安全性” 第1 部分 / 第2 部分 / 第3部分
讲座10：“符号执行” 第1 部分 / 第2 部分 / 第3部分
第11课：“ Ur / Web编程语言” 第1 部分 / 第2 部分 / 第3部分
讲座12：网络安全性第1 部分 / 第2 部分 / 第3部分
讲座13：“网络协议” 第1 部分 / 第2 部分 / 第3部分
第14课：“ SSL和HTTPS” 第1 部分 / 第2 部分 / 第3部分
第15课：“医疗软件” 第1 部分 / 第2 部分 / 第3部分
第16课：“侧面通道攻击” 第1 部分 / 第2 部分 / 第3部分

好的，让我们开始吧。 因此，今天我们将讨论通过边道攻击，这是所有类型系统固有的普遍问题。 从广义上讲，在您认为某些信息不能泄露有关系统的信息的情况下，会发生通过边道的攻击。



通常，您具有几个在用户和服务器之间建立连接的组件。 同时，您认为您知道通过连接这两个订户的这条导线通过的所有信息，知道了用户和服务器相互交换的所有比特，这是安全的。 但是经常会发生某些信息仍被用户或服务器披露的情况。 今天的讲座中描述的示例描述了这样一种情况，即用户和服务器之间的消息同步仅通过观察这些订户之间的比特流即可揭示一些您不知道的附加信息。

实际上，您可以担心种类繁多的副渠道。 人们了解到40年代边通道的出现，他们发现如果您开始在电传打字机上键入字符，那么电传打字机电子设备将开始发出射频辐射。 在这种情况下，您可以简单地将示波器放在其旁边，并观察无线电信号的频率如何根据电传打字员打印的符号而变化。 因此，RF辐射是使您担心的旁通道的经典示例。

人们还注意到许多其他示例，例如电力消耗。 这是您可以担心的另一个辅助渠道，因为您的计算机将根据计算结果使用不同量的能量。



旁通道的示例是声音，由于该原因，信息泄漏也是可能的。 例如，人们聆听打印机，并根据他们发出的声音判断打印的字符。 对于在打印过程中产生非常烦人的声音的点矩阵打印机，这尤其容易。

通常，这是要考虑的事情。 在周一的一次演讲中，凯文还提到了他在研究中涉及的一些有趣的副渠道。 但是，我们将研究David Bramley和Dan Bone研究的特定副渠道。 在大约10年前发表的工作中，他们写道，他们能够通过测量对恶意客户端各种输入数据包的不同响应的时间来提取Apache Web服务器的加密密钥。 在这种特殊情况下，他们“搜寻”了一个加密密钥。 实际上，通过边信道进行的许多攻击都将加密密钥作为目标，部分原因是很难通过这样的信道获取大量数据。 加密密钥是输出少量比特的情况之一，也就是说，在攻击过程中，攻击者可以提取大约200-256比特的信息。 但是仅基于这200位，它们就可以破解此Web服务器的加密密钥。

如果您试图进入某种具有社会保险号的数据库，则将需要“合并”很多信息。 这就是为什么大多数旁通道攻击都将重点放在获取小秘密（如加密密钥或密码）上的原因。 但总的来说，这适用于许多其他情况。

在讲座材料中，还描述了另一个很酷的东西-这就是所有这些都可以通过网络完成。 您可能意识到他们必须做很多细致的工作才能捕捉到时间信息中这些微小的差异。 他们发送到服务器的每个请求与另一个请求相差1-2微秒，这是很短的时间。 因此，您应该非常小心，因为我们的网络不允许我们发现这种暂时的差异，并确定服务器处理您的请求的时间比应处理的时间长1-2微秒。



结果，尚不清楚是否可以在非常“嘈杂”的网络中组织此类攻击，因为应将有用的信息与噪声水平分开。 这些家伙是最早显示出您可以真正通过以太网进行此操作的人，其中以太网在网络的一端，而客户端在另一端。 他们证明，确实有可能部分地通过平均，部分地通过其他技巧来测量这些差异。
本讲座其余部分的计划如下-首先，我们深入研究这些人使用的RSA公钥密码算法。 我们不会从安全性的角度评估它，但是我们将看到它是如何实现的，因为对于使用旁通道来说，算法的实现至关重要。

Bramley和Bone详细审查了各种实现细节，以了解某些事物执行得更快或更慢的时间。 因此，首先我们需要找出RSA密码系统的实现方式，然后再回去找出如何攻击RSA中所有可用的结构。

让我们从高级别回顾RSA开始。 RSA是相当广泛使用的公钥密码系统。 几周前，当我们谈论证书时，我们提到了这些家伙。 现在，我们将看看它是如何工作的。

通常，您需要担心3件事-这就是密钥生成，加密和解密。 在RSA中，创建密钥的方法是选择2个大质数整数，用p和q表示它们。 这些家伙在他们的文章中分别写有p和q，大小均为512位。 通常将其称为1024位RSA，因为这些素数的乘积是1000位整数。 如今，这对于RSA密钥大小来说可能不是一个好的选择，因为破解它对于攻击者而言是相对容易的任务。 因此，如果10年前1000位似乎是一个合理的数目，今天在构建系统时，则应选择2000、3000甚至4000位RSA密钥。 因此，RSA密钥大小意味着这些素数的大小。

然后，为方便起见，我们将讨论数字n，它只是这些素数n = pq的乘积，该数字称为模块。 因此，既然我们知道如何创建密钥或密钥的至少一部分，我们将必须弄清楚如何对消息进行加密和解密。



而我们加密和解密消息的方式是基于提高以n为模的数字的幂。 似乎有些奇怪，但我们会在一秒钟内解决。 因此，如果要加密消息m，则必须通过mod n将其转换为me。 e的值是一个度数，我们将在一秒钟内弄清楚如何选择它。 这就是我们要加密消息的方式。

也就是说，我们只是将此消息视为整数并将其提升为幂。 稍后，我们将了解其工作原理，但现在，我们将使用字母C表示所有此加密消息。

然后，为了解密它，我们必须找到另一个有趣的指数d，它使我们能够获取加密的消息C，将其提高为模n的幂d，从而神奇地获得解密的消息m。

因此，一般原则是使用一个指数来加密消息，而使用另一个指数来解密消息。



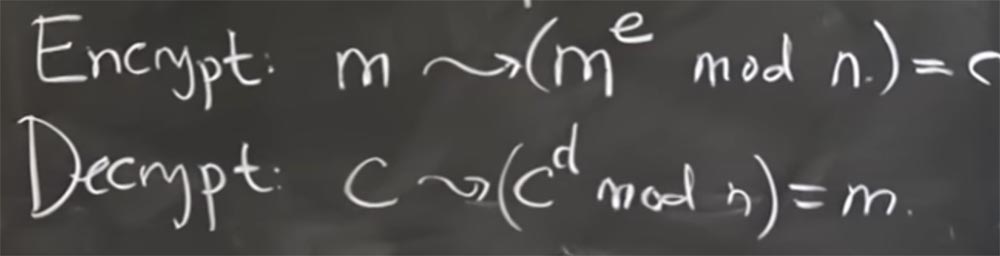
总而言之，似乎很难理解我们将如何得出这两个魔术数字，从而以某种方式返回给我们原始信息。 但是，如果您看一下这个数字n的乘幂或乘法运算的模数，那么您将了解所有内容。

如果我们取X并将其提高到等于n的函数φ的幂，那么它将为1模n：

^Xφ（n） = 1模n

对于我们对n的特定选择，此phi函数非常简单；它等于φ=（p-1）（q-1）。
然后，开放指数e乘以秘密指数d大于1但小于φ（n）的乘积将等于：

ed =ɑ（n）+1，其中ɑ是一个常数。

因此，可以正确地解密消息，因为如果知道φ（n）的值以便计算考虑到e的e或考虑到d的e，则有一个相当简单的算法。

受众： 1模n是否等于1？

教授：是的，我在这里犯了一个错误，平等应该是这样的：

^Xφ（n） _{mod n} = 1 mod n，即，从n模n开始的函数“ fi”的度数中的X值等于n模n。

这基本上意味着对于RSA，我们必须选择一些e值，这将是我们的加密值。 然后根据公式de = 1 modφ（n）从e生成d，因此d = 1 / e modφ（n）。



有一些欧几里得算法可以有效地用于此计算。 但是，为此，您必须知道φ（n），这需要分解，即将我们的数n分解为因子p和q。

因此，RSA是一个系统，其中公用密钥是一对：加密指数e和数字n，而对d和n是保密的私有密钥。 因此，任何人都可以提高为您加密它的能力。 但是只有您知道d的这个值，因此您可以解密消息。 并且，直到您知道这些因子P和Q或N等于P和Q的乘积的因式分解，您才知道φ=（p-1）（q-1）是什么。



结果，计算d的该值是一项相当困难的任务。 这就是高级RSA算法的全部意义。

既然我们已经熟悉了RSA的原理，那么我想谈谈两点。 关于如何正确使用它的技巧，使用它时会出现一些陷阱。 有许多方法可以实现此幂运算的代码并高效地执行。 这是一项非常艰巨的任务，因为我们正在处理1000位整数，您不能仅对其执行乘法指令。 完成这些操作可能会花费很长时间。

因此，我首先要提到的是RSA的各种陷阱。 其中之一是乘法性。 假设我们有2条消息：m ₀和m ₁ 。 我将它们加密，将m ₀转换为m ₀ ^e mod n，将m1转换为m ₁ ^e mod n。 一个可能的问题，或者不一定是问题，但是对于使用RSA的人来说，一个不愉快的惊喜是，用m ₁加密乘积m ₀非常容易，因为您只需将这两个数字相乘即可：m ₀ ^e mod n * m ₁ ^e mod n。



如果将它们相乘，将得到模n的乘积（m ₀ m ₁ ）。 这是正确的加密，简化了RSA的m ₀ m ₁值使用。 目前这不是什么大问题，因为您可以简单地创建此加密的消息，但不能对其解密。 但是，通用系统可能会允许您解密特定消息。 也就是说，如果它允许您解密创建的消息，那么也许通过遵循反向路径，您可以找出这些消息分别是m ₀和m ₁ 。

这个事实不容忽视，因为它影响许多使用RSA的协议。 在讲座的最后，我们将使用一种属性作为防御机制。

您要注意的第二个陷阱或RSA属性是确定性或可确定性。 在前面描述的基本实现中，如果采用消息m并对其进行加密，然后将其转换为m ^e mod n，则这是确定性消息功能。 因此，如果再次对其进行加密，则将获得完全相同的加密。

这不是理想的属性，因为如果我看到您正在发送使用RSA加密的某些消息，并且想知道它是什么，那么对我来说很难解密它。 但是我可以尝试不同的方法，结果我看到您正在发送此消息。

然后，我将其加密，看看是否得到相同的加密文本。 如果是这样，那么我将发现您已加密。 因为我需要加密的消息是一个公共可访问的公共密钥，它是一对数字（n，e）。

因此，这并不是很好，并且在使用RSA时您可能必须小心使用此属性。 因此，这种原语很难直接使用。



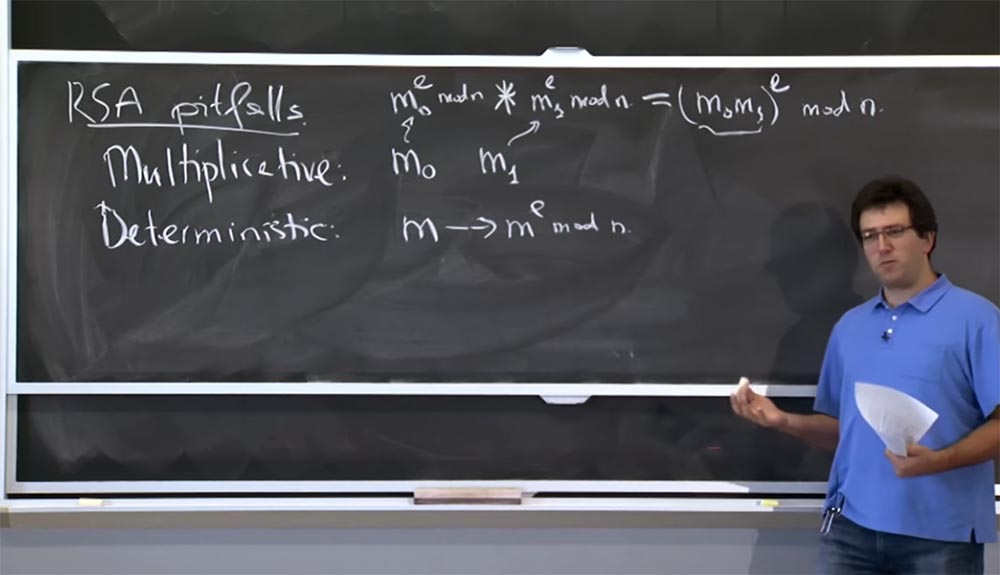
实际上，为了避免RSA出现类似问题，人们在加密之前以某种方式对消息进行编码。 他们没有直接将消息提升为幂，而是采用了某种消息函数并将其提升为幂为n：

[f（m）） ^e mod n。

今天通常使用的该函数f称为OAEP-加法最佳非对称加密。 这是用两个有趣的属性编码的。

首先，它带来了随机性。 您可以将f（m）视为生成要加密的1000位消息。 该消息的一部分将是您在矩形中间的消息。 当然，您可以在解密时取回它。 因此，您需要做2件有趣的事情：在右边放置某种随机性，即r的值。 它给出了如果您多次加密一条消息，则每次都会得到不同的结果，因此将不再确定加密。

为了克服这种乘法性质和其他类型的问题，左侧有一个填充板，它是1 0 1 0 1 0类型的序列。您可以选择一个更好的序列，但是粗略地说，这是某种可预测的序列，您在此处插入，并且每当解密邮件时，请确保此序列仍然存在。 乘法将破坏这些填充位，然后您将清楚地知道有人弄乱了您的消息并将其丢弃。 如果这些位保留在原位，则表明没有人伪造了您的消息，并且您可以接收该消息，因为该消息已被某人正确加密。



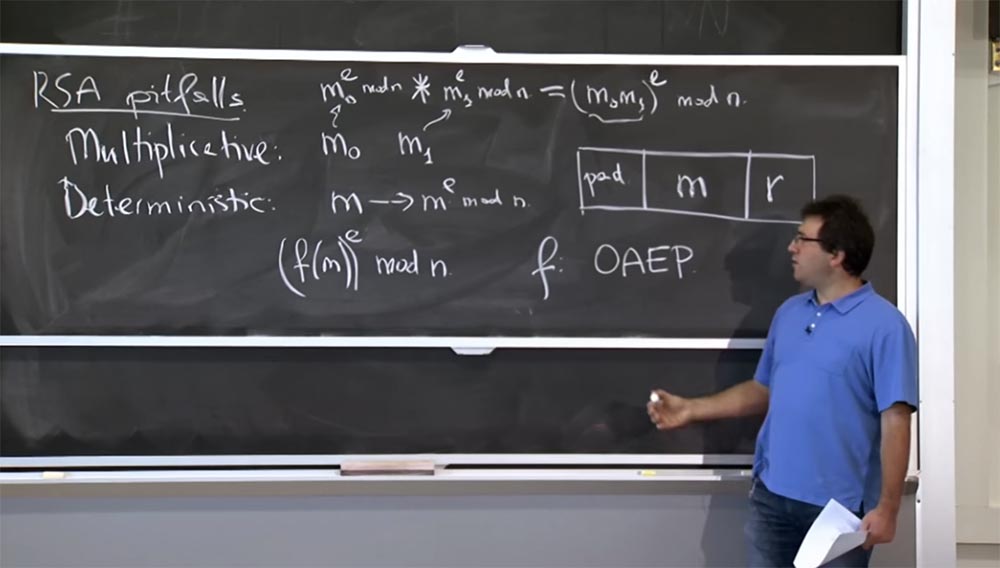听众：如果攻击者知道填充值有多大，他可以将1设置在序列的最底部，然后将该值相乘吗？

教授：是的，也许。 这有点复杂，因为这种随机性r将继续下去。 因此，此OAEP的具体设计比我描述的要复杂一些。 但是，假设这是整数而不是按位乘法，那么随机性会进一步扩展，因此您可以创建一个不会发生这种情况的OAEP方案。

事实证明，您不应该直接使用此RSA数学运算，实际上，您应该使用某种可以以正确方式为您实现所有这些功能的库，并将其用作加密和解密参数。

但是，上面讨论的细节对我们来说是有价值的，因为我们实际上是在试图找出如何破坏或攻击现有的RSA实现。

特别是，在演讲文章中描述的攻击将利用以下事实：服务器在收到消息时将要测试该填充附件。 因此，这就是我们要考虑服务器解密所需的时间。 我们将发送一个精心构造的消息，但是它不是根据真实消息m及其加密创建的。 我们将创建一个彻底的加密整数值。

服务器将尝试对其进行解密，并且会出现某种荒谬性，与之很可能无法配对，因此服务器将立即拒绝此消息。 , , , , : RSA, , . , . , .

, , RSA. , , , . , , , 1000 . e .



, . , 1000 . 1000- , 1000 1000 n, . RSA , .
4 , . , . , CRT. . . , , , , [ = a ₁ ] mod p [ = a ₂ ] mod q, q – , .



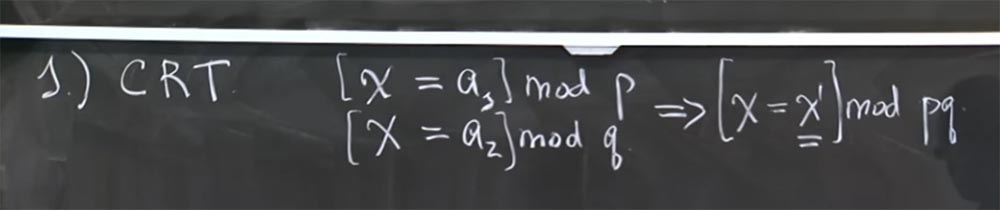
, [ = ¹ ] mod pq. ¹ , . ¹ , mod pq a ₁ a ₂ mod p q.

, ? , , n, p q.



, mod pq, mod p mod q. , , mod pq. , ? , , ?

: , ?

: , , , . , p q, n 1000 , p q 500 , . , , — , , . — . , , . 1000 512 , 2 . , 4 . [ = a ₁ ] mod p [ = a ₂ ] mod q , 4 . 2 RSA , .

, .

, Sliding windows, « ». . , .



, - , 500 , mod p mod q, d. c d? , c d . d , 500, . , , . , « ». .

c ^2x , : (c ^x ) ² :

c ^2x = (c ^x ) ²

c ^2x , 2 , cx, . , , c ^2x+1 :

c ^2x+1 = (c ^x ) ² x

.

, , , . , , , . , .

« », ? , . , , « » c ^2x+1 = (c ^x ) ² x .

, , , – , c ^2x+1 c ^2x , c. , , . , .



, :

1
3
7
...
31

. , , , .

, ^32x+y , 5 , 32- , ^y .



³² . , , , , c . «» .

29:00

麻省理工学院的课程“计算机系统安全”。 16: « », 2


.

感谢您与我们在一起。 你喜欢我们的文章吗？ 想看更多有趣的资料吗？ 通过下订单或将其推荐给您的朋友来支持我们， 为我们为您发明的入门级服务器的独特模拟，为Habr用户提供30％的折扣： 关于VPS（KVM）E5-2650 v4（6核）的全部真相10GB DDR4 240GB SSD 1Gbps从$ 20还是如何划分服务器？ （RAID1和RAID10提供选件，最多24个内核和最大40GB DDR4）。

VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps , .

戴尔R730xd便宜2倍？ 仅在荷兰和美国，我们有2台Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100电视（249美元起） ！ 阅读有关如何构建基础架构大厦的信息。 使用价格为9000欧元的Dell R730xd E5-2650 v4服务器的上等课程？