麻省理工学院的课程“计算机系统安全”。 第16课：通过边道攻击，第2部分

麻省理工学院。 讲座课程＃6.858。 “计算机系统的安全性。” Nikolai Zeldovich，James Mickens。 2014年

计算机系统安全是一门有关开发和实施安全计算机系统的课程。 讲座涵盖了威胁模型，危害安全性的攻击以及基于最新科学研究的安全技术。 主题包括操作系统（OS）安全性，功能，信息流管理，语言安全性，网络协议，硬件安全性和Web应用程序安全性。

第1课：“简介：威胁模型” 第1 部分 / 第2 部分 / 第3部分
第2课：“控制黑客攻击”， 第1 部分 / 第2 部分 / 第3部分
第3讲：“缓冲区溢出：漏洞利用和保护” 第1 部分 / 第2 部分 / 第3部分
讲座4：“特权分离”， 第1 部分 / 第2 部分 / 第3部分
讲座5：“安全系统从何而来？” 第1 部分 / 第2部分
讲座6：“机会” 第1 部分 / 第2 部分 / 第3部分
讲座7：“本地客户端沙箱” 第1 部分 / 第2 部分 / 第3部分
讲座8：“网络安全模型” 第1 部分 / 第2 部分 / 第3部分
讲座9：“ Web应用程序安全性” 第1 部分 / 第2 部分 / 第3部分
讲座10：“符号执行” 第1 部分 / 第2 部分 / 第3部分
第11课：“ Ur / Web编程语言” 第1 部分 / 第2 部分 / 第3部分
讲座12：网络安全性第1 部分 / 第2 部分 / 第3部分
讲座13：“网络协议” 第1 部分 / 第2 部分 / 第3部分
第14课：“ SSL和HTTPS” 第1 部分 / 第2 部分 / 第3部分
第15课：“医疗软件” 第1 部分 / 第2 部分 / 第3部分
第16课：“侧面通道攻击” 第1 部分 / 第2 部分 / 第3部分

受众：如何首先确定x和y？

教授：为此，您必须以二进制形式查看参展商。 假设我尝试计算c ^1011010的值，则度数可能还包含更多位数。 如果要重新平方，则需要查看最低位-这里是0。



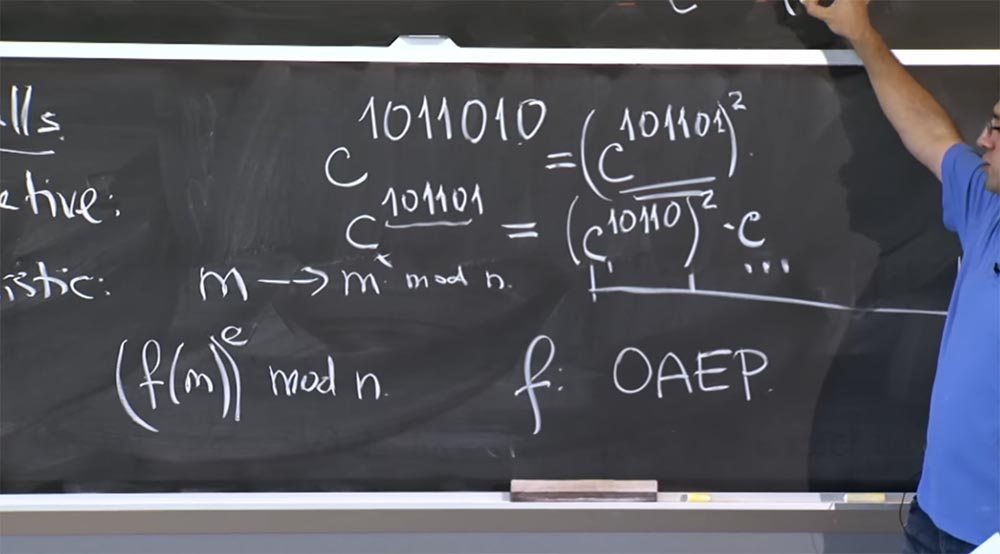
因此，我们得到等式c ^1011010 =（c ¹⁰¹¹⁰¹ ） ²

接下来，我们需要计算c ¹⁰¹¹⁰¹ ，在这里我们不能使用此规则，因为它不是2x-它是x加1。因此，我们编写以下等式：

c ¹⁰¹¹⁰¹ =（c ¹⁰¹¹⁰ ） ² c，因为此前缀101101 = 10110 + 1。

因此，我们将平方乘以c，以便使用它来重新平方。

对于“滑动窗口”，我们需要从低端捕获更多位。 如果您想在此处使用“滑动窗口”而不是从此处提取一个s来技巧，那么考虑到这个巨大的表，我们一次可以使用3位，并坚持使用c7。 如果取度的前3位，则得出c ¹⁰¹¹⁰¹ =（c ¹⁰¹ ） ⁸ c ¹⁰¹ 。

在这种情况下，我们对（c ¹⁰¹ ） ⁸的计算量实际上是相同的，但是您可以在表中看到c ¹⁰¹的值。 （c ¹⁰¹ ） ⁸形式的部分表示您将使用“滑动窗口”来计算其值。



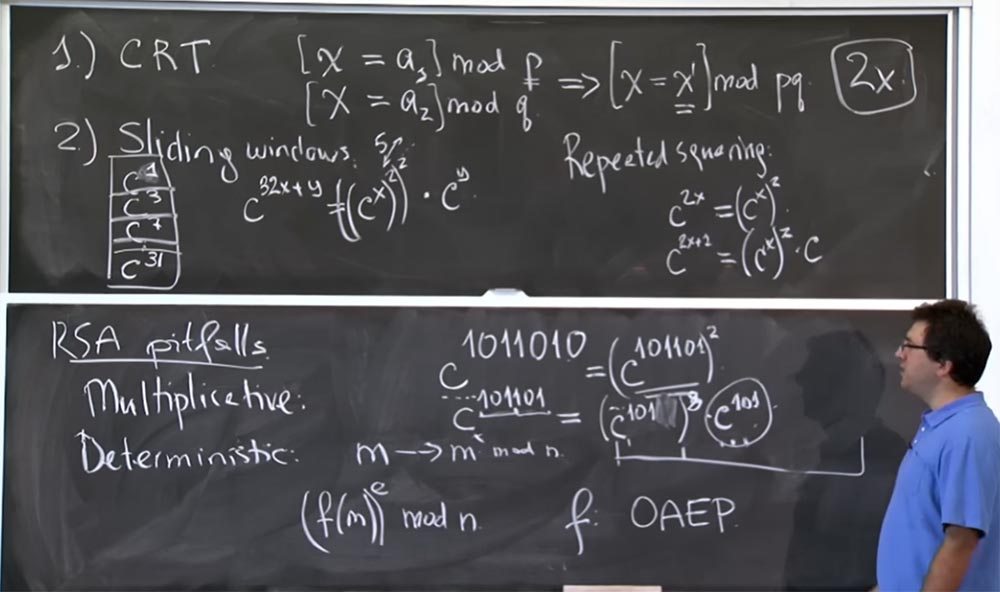
这样可以节省大量时间，因为可以使用预乘值。 10年前，据信就计算效率而言，最高达32度的值表是最佳计划，因为这里存在某种折衷办法，对吧？ 您花时间创建此表，但是如果您不打算经常使用某些记录，则表不要太大。 假设如果创建的表的值最大为c ⁵⁰⁰度，但是您不打算使用值大于128的指数，那么只会浪费时间。

听众：有什么理由不提前创建这么大的桌子？ 也就是说，要计算可以在计算中规避的有限度数的值？

教授：如果您不想提前执行体积计算……那么，有两件事。 一种是，您应该有一个代码来检查表中的所需记录是否已满，这可能会降低预测CPU进程分支的准确性。 同时，在一般情况下，处理器将运行得更慢，因为它必须检查所需的记录是否在表中。 第二点有点令人讨厌，它可能是通过各种辅助通道（即通过缓存访问模式）泄漏表条目。 因此，如果您在同一处理器上运行其他进程，则可以看到哪些缓存地址已从缓存中删除或放慢了速度，因为有人可以访问记录c ³或记录c ³¹ 。 该表越大，越容易确定用于创建RSA密钥的指数位。

该巨型表能够确定处理器丢失了哪个缓存地址，即表明加密过程应该可以访问该表中的该条目。 反过来，这告诉您给定的位序列出现在私钥的指数中。 因此，我认为从数学上讲，您可以根据需要填写此表，但实际上，您不希望它变成巨大的规模。 此外，您将无法有效使用庞大的表条目。 重复使用相对较小的表的记录要有用得多，例如，计算c ^7时，可以两次使用c ³值，依此类推。

因此，这是通过重新平方和“滑动窗口”方法进行的RSA优化。 我不知道他们是否仍使用这种大小的“滑动窗口”，但是无论如何它都会加快计算过程，因为否则您将必须对指数的每一位求平方，然后乘以每一位。 因此，如果您有500位指数，那么您将必须完成500个平方并乘以c约256个乘法。 对于“滑动窗口”，您仍然必须制作512个正方形，因为这无法避免，但是由于使用了表中的条目，与c的乘数将从256减少到大约32。

这是一般的优化计划，可将计算过程加快大约一倍半。 这是一个相当简单的优化。 有两个带数字的巧妙技巧，可以使乘法过程更有效。

第一个是蒙哥马利变换，第二个是为什么这对我们特别重要。 这种优化正试图为我们解决一个问题，那就是每次进行乘法运算时，我们得到的数字都会以递增的顺序不断增长。 特别是，在“滑动窗口”和重新平方中，当您将c提高到y的幂时，实际上会将两个数字相乘。

问题在于，如果用于乘法的输入数据c ^x和c ^y分别为512位，则乘法结果的大小将为1000位。 之后，您将获得1000位结果，然后再将其乘以512位，结果大小分别为1500、2000、2500位，并且一切都在增长。

但是，您不希望这样做，因为乘法会增加被乘数的顺序。 因此，由于所有这些计算都是mod p或mod q，因此我们必须使数字大小尽可能小，基本上等于512位。

我们可以减少这个数字，例如，我们要计算（（（c ^x ） ² ） ² ） ² 。 例如，您可以做的是计算cx模p，然后将其再次对p求平方，再对p求平方。 这种方法比较好，因为它使我们可以将数字的大小保持在512位以内，即尽可能地小。 从减小我们需要相乘的数字的大小的角度来看，这是很好的，但实际上，使用此模块p的运算会显着“增加计算成本”。



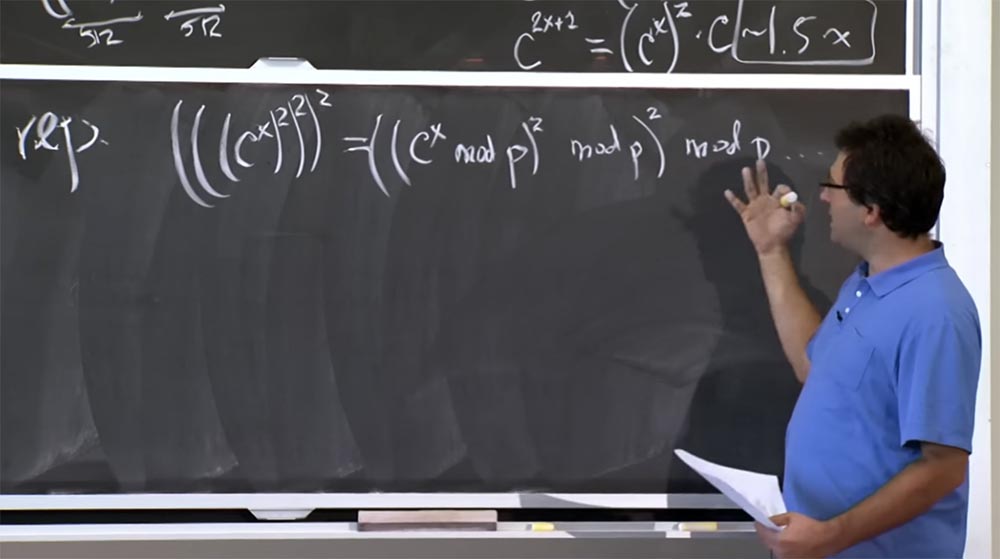
因为获得mod p的方式是除法。 除法比乘法差。 我不会列出除法算法，但是速度很慢。 通常，您会尽量避免除法运算，因为这不容易编程。 事实是您需要使用某种近似算法，牛顿方法等，所有这些都会减慢计算过程。

乘法更有利可图，但是使用mod p或mod q运算来减小数字大小将比乘法花费更多。 我将向您展示一种避免这种情况的方法，以及如何使用蒙哥马利变换进行快速计算。

基本思想是以蒙哥马利变换的形式表示要相乘的整数。 这实际上很容易。 为此，我们只需将数字a乘以某个神奇的值R即可。一秒钟后，我将告诉您它是什么。 但是，让我们首先找出当我们选择R的任意值时会发生什么。

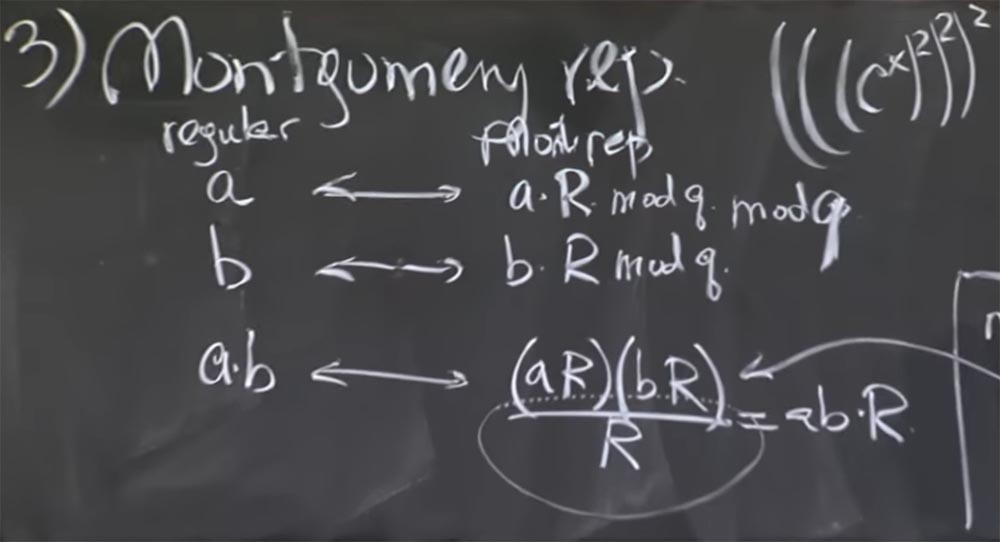
因此，我们取2个数字a和b，并将它们转换为Montgomery表示形式，将每个数字乘以R。然后，Montgomery变换中a和b的乘积将如下所示：

ab <->（aR）（bR）/ R = abR

也就是说，将aR乘以bR并得到ab乘以R的平方。 现在我们有两个R，这有点烦人，但是您可以将其除以R。结果，我们得到ab与R的乘积。不清楚我们为什么需要再次将该数字相乘。 首先让我们找出这是否正确，然后我们将理解为什么它会更快。
从很容易的意义上说，这是正确的。 如果您想将一些数字相乘，则需要将它们乘以R的此值并获得蒙哥马利变换。 每次我们将这两个数字相乘时，必须将它们除以R，然后查看abR形式的转换结果形式。 然后，当我们完成平方，乘法和所有这些操作后，我们将返回到结果的正常普通形式，最后一次简单地除以R。



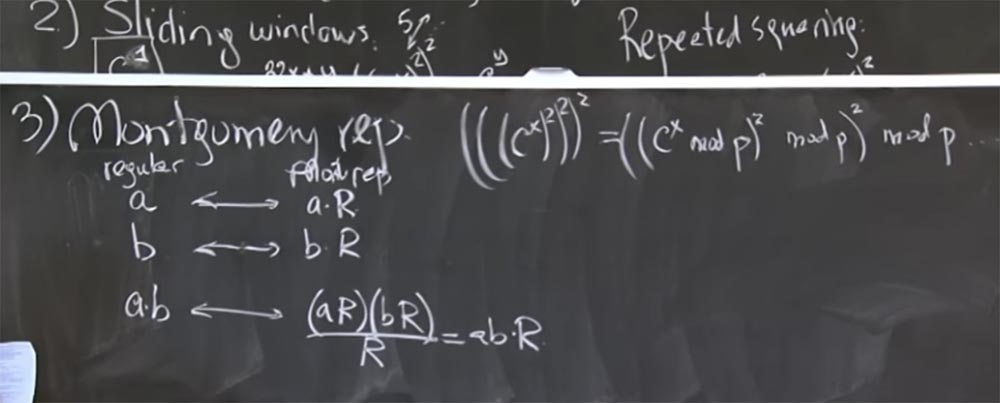
现在考虑如何为R选择最合适的数字，以使R的除法变得非常快。 最酷的是，如果R除以很小的数时很快，并且我们不必太频繁地执行此mod q。 尤其是，假设aR的大小也约为500位，因为这实际上是mod p或mod q。 因此，aR为500位，bR也将为500位，因此乘积（aR）（bR）将为1000位。 R也将是一个方便的500位数字，大小为p。 而且，如果我们可以使除法运算足够快，那么ab的结果也将约为500位数字，因此我们可以进行乘法运算而无需进行其他除法运算。 除以R会更有利可图，并且给我们带来很小的结果，这避免了在大多数情况下使用mod p。

那么，我一直在谈论的这个奇怪的R号码是什么？ 其值是2到512度：

R = ²⁵¹²

它是1和一堆零，因此很容易乘以这样的数字，因为它足以在结果中加上一堆零。 如果结果的最低有效位为零，则除法也很简单。 因此，如果您从一个带有512个零的位堆中得到一个值，那么除以2至512度将非常简单-您只需在右侧放零即可，这是一个完全正确的除法运算。

一个小问题是，当您进行乘法运算时，实际上我们的右边没有零。 我们使用所有512位有真实的512位数字。

（aR）与（bR）的乘积也是1000位数量级的实数，因此我们不能只丢弃最低有效位。 但是一种合理的方法是基于这样一个事实，即让我们担心的唯一事情就是mod p的值。 因此，您始终可以将多个p添加到该值，而无需更改其等效p。 结果，我们可以添加p值的倍数，以便所有最低有效位都为零。 让我们看一些简单的例子。 我不会在板上写512位，但是我仅举一个简短的例子。

假设在我们的情况下R = 2 ⁴ =10000。这比实际大小小得多。 让我们看看蒙哥马利变换的工作原理。 我们尝试计算mod q，其中q = 7。 二进制形式的q = 7是（111）。

进一步假设我们执行了一些乘法（aR）（bR），并且用二进制表示，结果是11010，即，这将是乘积（aR）（bR）的值。 我们如何将其除以R？

显然，并非所有四个最低有效位都为零，因此我们不能仅将它们分开，而是可以添加q的倍数的数量。 特别是，我们可以在q中加2倍，二进制表示形式为2q = 1110。 作为加法的结果，我们得到101000，我希望我做的一切正确。



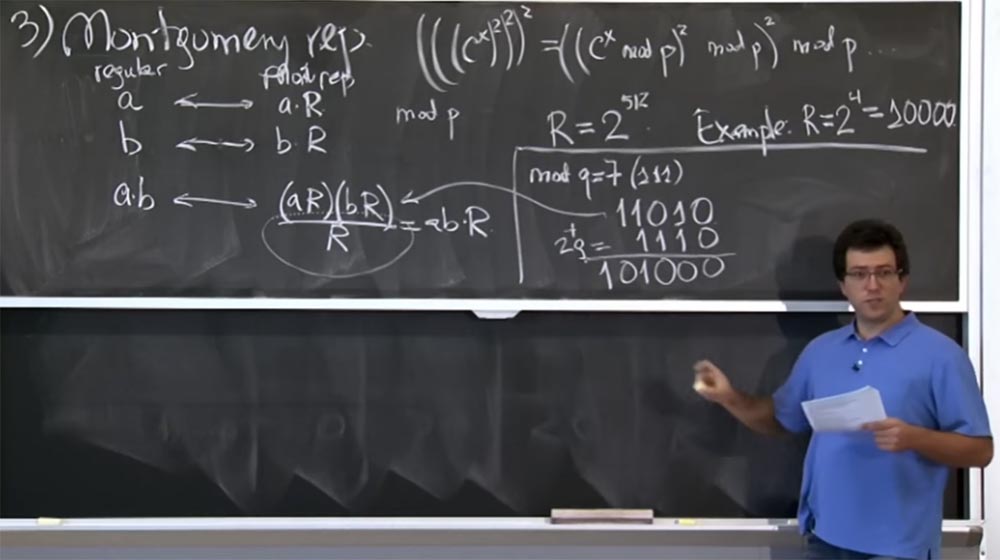
这样我们得到了总和（aR）（bR）+ 2q。 实际上，我们不在乎+ 2q，因为我们只关心mod q的值。 现在我们离目标更近了，因为在右边有三个零。 现在我们可以添加更多q。 假设这次是8q，即111000。再次添加行，得到1100000。现在我们有了原始的（aR）（bR）+ 2q + 8q =1100000。最后，我们可以很容易地将其划分为R，只是掉了四个低零。



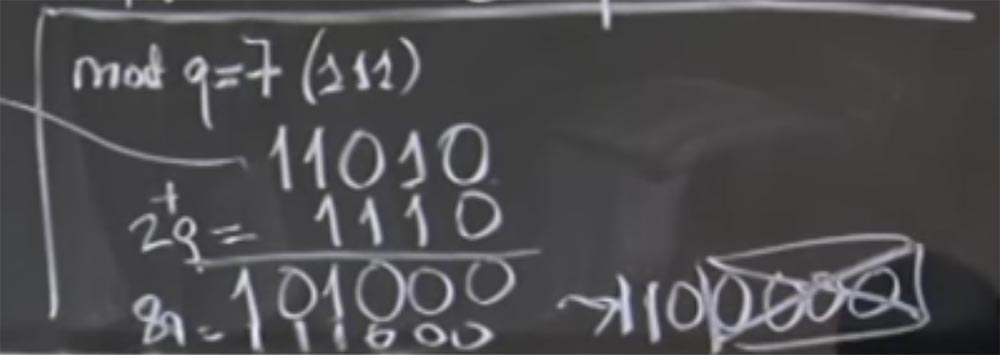受众：乘积（aR）（bR）总是以1024个零结尾吗？

教授：不，我将解释可能造成的混乱。 假设数字a为512位，我们将其乘以R得到一个1000位的数字。 在这种情况下，您是对的，aR是高位是a，低位都为零的数字。 但是然后我们执行mod q使其变小。 因此，一般情况下1024位的大小是偶然的，因为该数字仅在第一次转换时才具有这些低0，但是在您进行了几次乘法运算后，它将是任意位。

为了避免误导您，我必须在aR之后和bR之后在此处写mod q-在这里我将其添加-并在进行转换以减小该值后立即计算此mod q。



初始转换相当费力，或者至少与乘法中的常规调制一样昂贵。 很棒的事情是，在进行蒙哥马利转换时，您只需支付一次价格，然后，而不是在计算的每个步骤将其转换回去，只需将其保持为蒙哥马利视图的形式即可。
请记住，要提高到具有512位的幂，您将必须执行500次以上的乘法运算，因为我们必须至少执行500个平方以及更多的平方。 因此，如果保持这种表示数字的形式，则需要两次进行mod q运算，然后进行很多简单的除法运算。 最后，用R除以返回此表格ab。

因此，您无需对乘法的每一步进行500次mod q运算，而是对mod q进行两次运算，然后以最小的成本继续进行R的除法运算。
受众：当您将q的倍数相加然后除以R时，是否有余数？
教授：实际上，q是除以q的余数。 简单地说，x + yq mod q = x。 在这种情况下，还有另一个有用的属性-所有模块都是质数。 如果您拥有（x + yq / R）mod q，那么它等于x / R mod q，这是事实。



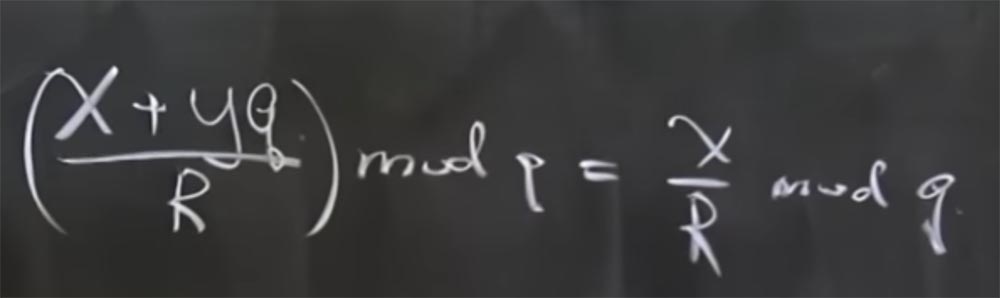
这样做的原因是，模块化算术中没有真正的除法运算，而只是倒数。 实际上，这意味着如果我们将（x + yq）乘以mod q计算出的倒数R，则等于两个乘积之和：mod q倒数R的乘积x和mod q乘以yq的倒数R的乘积。 此外，最后一项减少了，因为它乘以q。



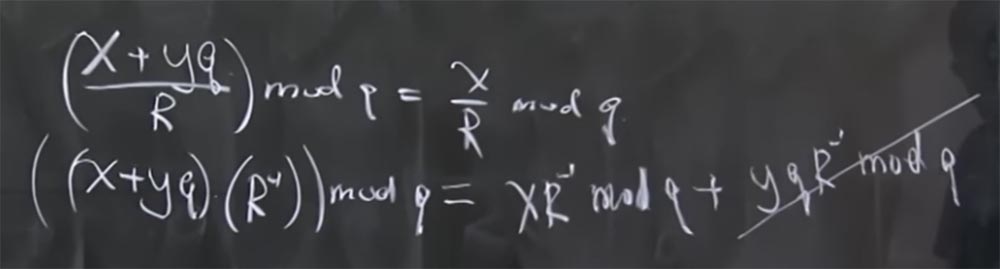
对于诸如求和2q，8q之类的事情，有一个公式可以加快计算过程。 我逐渐做到了，首先计算了2q，然后计算了8q，依此类推，但是讲义材料有一个完整的公式可以使用，我只是不想浪费时间在黑板上写下它。 它允许您计算必须加的q值的倍数，以便所有最低有效位都变为0。然后证明，要进行R除，您只需要计算q的此幻数，将其相加，然后舍弃低零位，无论结果大小如何，都将使您的数字返回512位。

但是有一个微妙之处。 我们谈论这个问题的唯一原因是，这里发生了一些有趣的事情，这使我们能够找到有关计时的信息。 特别是，尽管我们除以R，但我们仍然知道结果将约为512位。 但是它仍然可以大于q，因为q不是512位数字，所以它可能比R小一点。

因此可能是在我们用R进行了有利的除法之后，可能需要再次减去q，因为我们得到的东西很小，但仍然不够小。 因此，在除法之后，我们可能不得不再次减去q。 并且此减法可以用作攻击的一部分，因为减法运算会增加计算时间。



而且有人发现-不是这些人，而是先前工作中的某人-有机会做称为额外减少或额外减少的事情。 , . , xd mod q, - x mod q, 2R. .



, x mod q , . , cd.



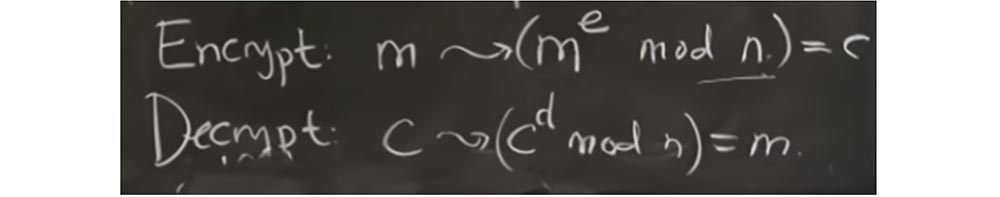
, extra reduction , X , , , q.



, c, extra reduction , c — q. , , q . , extra reduction, , , X mod q , = q + έ, . , . , , , , extra reduction .

: , ?

: , extra reduction? , , , . , . , , extra reduction, , , . , . , , mod q. , , , . , mod q , , .

, . , - , . — , . , - , extra reduction .

, . , OpenSSL, , . , mod q . , , .

, , , , a b. — 512- . , 32- , , 64- ? ?



- ? , , a b .

, , 512 , 64- , 32- . a : a ₁ a ₀ , a ₀ , a ₁ — . b – b ₁ b ₀ .

ab 3- : a ₁ b ₁ , a ₀ b ₀ , a ₁ b ₀ + a ₀ b ₁ . .



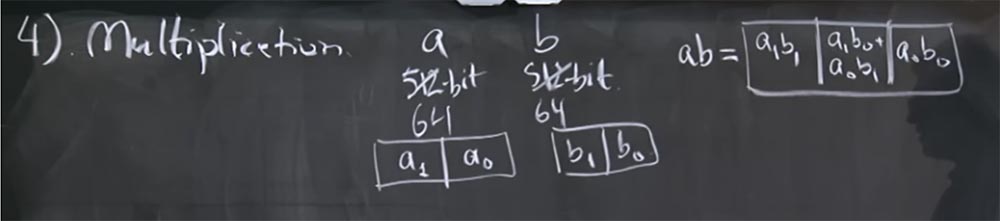
55:00

麻省理工学院的课程“计算机系统安全”。 16: « », 3


.

感谢您与我们在一起。 你喜欢我们的文章吗？ 想看更多有趣的资料吗？ 通过下订单或将其推荐给您的朋友来支持我们， 为我们为您发明的入门级服务器的独特模拟，为Habr用户提供30％的折扣： 关于VPS（KVM）E5-2650 v4（6核）的全部真相10GB DDR4 240GB SSD 1Gbps从$ 20还是如何划分服务器？ （RAID1和RAID10提供选件，最多24个内核和最大40GB DDR4）。

VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps , .

戴尔R730xd便宜2倍？ 仅在荷兰和美国，我们有2台Intel Dodeca-Core Xeon E5-2650v4 128GB DDR4 6x480GB SSD 1Gbps 100电视（249美元起） ！ 阅读有关如何构建基础架构大厦的信息。 使用价格为9000欧元的Dell R730xd E5-2650 v4服务器的上等课程？