🙎🏾 🚻 👩🏾‍🏫 朱莉娅和电磁场中带电粒子的运动 🙌🏼 🚣🏼 🔐

我们以最常见的进化方程式为例，增强了求解和可视化微分方程式的技能，请记住旧的Scilab，并尝试了解是否需要...剪切下的图片（千字节为700）

确保软件是最新的

julia>] (v1.0) pkg>update #   (v1.0) pkg> status Status `C:\Users\\.julia\environments\v1.0\Project.toml` [537997a7] AbstractPlotting v0.9.0 [ad839575] Blink v0.8.1 [159f3aea] Cairo v0.5.6 [5ae59095] Colors v0.9.5 [8f4d0f93] Conda v1.1.1 [0c46a032] DifferentialEquations v5.3.1 [a1bb12fb] Electron v0.3.0 [5789e2e9] FileIO v1.0.2 [5752ebe1] GMT v0.5.0 [28b8d3ca] GR v0.35.0 [c91e804a] Gadfly v1.0.0+ #master (https://github.com/GiovineItalia/Gadfly.jl.git) [4c0ca9eb] Gtk v0.16.4 [a1b4810d] Hexagons v0.2.0 [7073ff75] IJulia v1.14.1+ [`C:\Users\\.julia\dev\IJulia`] [6218d12a] ImageMagick v0.7.1 [c601a237] Interact v0.9.0 [b964fa9f] LaTeXStrings v1.0.3 [ee78f7c6] Makie v0.9.0+ #master (https://github.com/JuliaPlots/Makie.jl.git) [7269a6da] MeshIO v0.3.1 [47be7bcc] ORCA v0.2.0 [58dd65bb] Plotly v0.2.0 [f0f68f2c] PlotlyJS v0.12.0+ #master (https://github.com/sglyon/PlotlyJS.jl.git) [91a5bcdd] Plots v0.21.0 [438e738f] PyCall v1.18.5 [d330b81b] PyPlot v2.6.3 [c4c386cf] Rsvg v0.2.2 [60ddc479] StatPlots v0.8.1 [b8865327] UnicodePlots v0.3.1 [0f1e0344] WebIO v0.4.2 [c2297ded] ZMQ v1.0.0

让我们翻阅过去的指南

并进行问题陈述

带电粒子在电磁场中的运动

在带电粒子上 $q$ 迅速进入EMF $u$ 洛伦兹部队的行为： $\ vec {F} _L = q \左（\ vec {E} + \左[\ vec {u} \次\ vec {B} \右] \右）$ 。该公式在进行许多简化后才有效。忽略相对论的修正，我们认为粒子质量是恒定的，因此运动方程的形式为： $\ frac {d} {dt}（m \ vec {u}）= q \左（\ vec {E} + \左[\ vec {u} \次\ vec {B} \右] \右）$

我们沿电场指向Y轴，沿磁场指向Z轴，为简单起见，假定初始粒子速度位于XY平面中。在这种情况下，粒子的整个轨迹也将位于该平面中。运动方程将采用以下形式：

\左\ {\开始{矩阵} m \ ddot {x} = qB \点{y} \\ m \ ddot {y} = qE-qB \点{x} \结束{matrix} \ right。

$\左\ {\开始{矩阵} m \ ddot {x} = qB \点{y} \\ m \ ddot {y} = qE-qB \点{x} \结束{matrix} \ right。$

无法估量： $x ^ * = \ frac {x} {\ lambda}，\，y ^ * = \ frac {y} {\ lambda}，\，\ tau = \ frac {ct} {\ lambda}，\，B ^ * = \ frac {Bmc} {q \ lambda}，\，E ^ * = \ frac {Emc ^ 2} {q \ lambda}$ 。星号表示尺寸量，并且 $\ lambda$ -所考虑的物理系统的特征大小。我们获得磁场中带电粒子运动方程的无量纲系统：

\ left \ {\ begin {matrix} \ frac {d ^ 2x} {d \ tau ^ 2} = B \ frac {dy} {d \ tau} \\ \ frac {d ^ 2y} {d \ tau ^ 2} = EB \ frac {dx} {d \ tau} \ end {matrix} \ right。

$\ left \ {\ begin {matrix} \ frac {d ^ 2x} {d \ tau ^ 2} = B \ frac {dy} {d \ tau} \\ \ frac {d ^ 2y} {d \ tau ^ 2} = EB \ frac {dx} {d \ tau} \ end {matrix} \ right。$

让我们降低顺序：

\左\ {\开始{矩阵} \ frac {dx} {d \ tau} = U_x \\ \ frac {dy} {d \ tau} = U_y \\ \ frac {dU_x} {d \ tau} = BU_y \\ \ frac {dU_y} {d \ tau} = E-BU_x \ end {matrix} \对。

$\左\ {\开始{矩阵} \ frac {dx} {d \ tau} = U_x \\ \ frac {dy} {d \ tau} = U_y \\ \ frac {dU_x} {d \ tau} = BU_y \\ \ frac {dU_y} {d \ tau} = E-BU_x \ end {matrix} \对。$

作为模型的初始配置，我们选择： $B = 2$ 特斯拉， $E = 5 \ cdot 10 ^ 4$ 伏/米 $v_0 = 7 \ cdot 10 ^ 4$ 米/秒对于数值解，我们使用DifferentialEquations包：

代码和图形

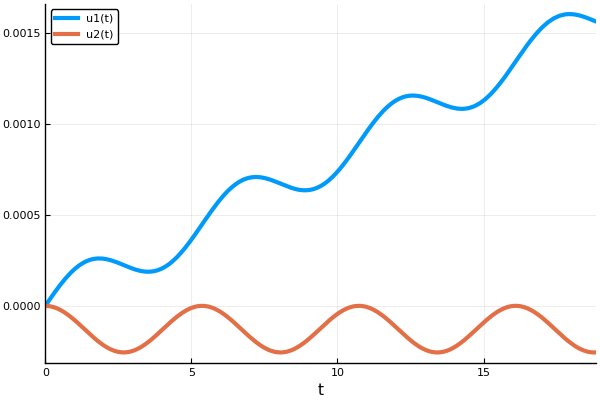
 using DifferentialEquations, Plots pyplot() M = 9.11e-31 # kg q = 1.6e-19 # C C = 3e8 # m/s λ = 1e-3 # m function modelsolver(Bo = 2., Eo = 5e4, vel = 7e4) B = Bo*q*λ / (M*C) E = Eo*q*λ / (M*C*C) vel /= C A = [0. 0. 1. 0.; 0. 0. 0. 1.; 0. 0. 0. B; 0. 0. -B 0.] syst(u,p,t) = A * u + [0.; 0.; 0.; E] # ODE system u0 = [0.0; 0.0; vel; 0.0] # start cond-ns tspan = (0.0, 6pi) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, Euler(), dt = 1e-4, save_idxs = [1, 2], timeseries_steps = 1000) end Solut = modelsolver() plot(Solut)

在这里，我们使用Euler方法，为此指定了步数。同样，不是系统的整个解决方案都保存在答案矩阵中，而是仅保存1和2个索引，即X和玩家的坐标（我们不需要速度）。

 X = [Solut.u[i][1] for i in eachindex(Solut.u)] Y = [Solut.u[i][2] for i in eachindex(Solut.u)] plot(X, Y, xaxis=("X"), background_color=RGB(0.1, 0.1, 0.1)) title!(" ") yaxis!("Y") savefig("XY1.png")#

检查结果。我们引入一个新变量而不是x $\波浪号{x} = x-ut$ 。因此，将转换为新坐标系，该坐标系相对于原始坐标系在X轴方向上以速度u移动：

\左\ {\开始{矩阵} \ ddot {\波浪号{x}} = qB \点{y} / m \\ \ ddot {y} = qE / m-qB \点{x} / m -qBu / m \结尾{matrix} \对。

$\左\ {\开始{矩阵} \ ddot {\波浪号{x}} = qB \点{y} / m \\ \ ddot {y} = qE / m-qB \点{x} / m -qBu / m \结尾{matrix} \对。$

如果你选择 $u = E / B$ 并表示 $\ omega = qB / m$ ，则系统将被简化：

\ left \ {\ begin {matrix} \ ddot {\ tilde {x}} = \ omega \ dot {y} \\ \ ddot {y} =-\ omega \ dot {\ tilde {x}} \ end {矩阵} \对。

$\ left \ {\ begin {matrix} \ ddot {\ tilde {x}} = \ omega \ dot {y} \\ \ ddot {y} =-\ omega \ dot {\ tilde {x}} \ end {矩阵} \对。$

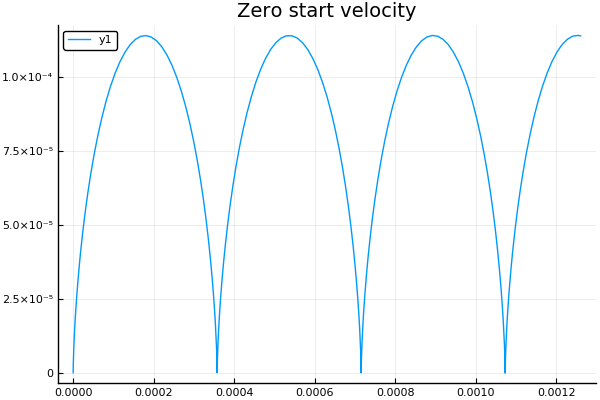
电场从最后的等式中消失了，它们是粒子在均匀磁场作用下的运动方程。因此，新坐标系（x，y）中的粒子应绕圆运动。由于此新坐标系本身会相对于原始坐标快速移动 $u = E / B$ ，则所得的粒子运动将包括沿X轴的匀速运动以及围绕XY平面中的圆的旋转。如您所知，将这两个动作加在一起时出现的轨迹通常是次摆线 。特别是，如果初始速度为零，则实现最简单的运动-沿摆线运动 。
让我们确保漂移速度确实等于E /V。 为此：

我们将设置一个故意较低的值而不是第一个元素（最大值），以破坏响应矩阵
我们在响应矩阵的第二列中找到最大元素的数目，该数目被纵坐标延迟
我们通过将最大横坐标值除以相应的时间值来计算无量纲漂移速度

 Y[1] = -0.1 numax = argmax( Y ) X[numax] / Solut.t[numax]

出： 8.334546850446588e-5

 B = 2*q*λ / (M*C) E = 5e4*q*λ / (M*C*C) E/B

出： 8.33333333333333333332e-5
高达七阶！
为了方便起见，我们定义了一个函数，该函数带有模型参数和图形签名，这些函数也将用作在项目文件夹中创建的png文件的名称（在Juno / Atom和Jupyter中可用）。与Gadfly不同，在Gadfly中 ，图形是在图层中创建然后由plot（）函数显示的，而在Plots中，为了在一帧中创建不同的图形，第一个图形是由plot（）函数创建的，随后的图形是使用plot！（）添加的 。习惯上在Julia中更改接受对象的函数名称以感叹号结尾。

 function plotter(ttle = "qwerty", Bo = 2, Eo = 4e4, vel = 7e4) Ans = modelsolver(Bo, Eo, vel) X = [Ans.u[i][1] for i in eachindex(Ans.u)] Y = [Ans.u[i][2] for i in eachindex(Ans.u)] plot!(X, Y) p = title!(ttle) savefig( p, ttle * ".png" ) end

如预期的那样，在零初始速度下，我们得到一个摆线：

 plot() plotter("Zero start velocity", 2, 4e4, 7e4)

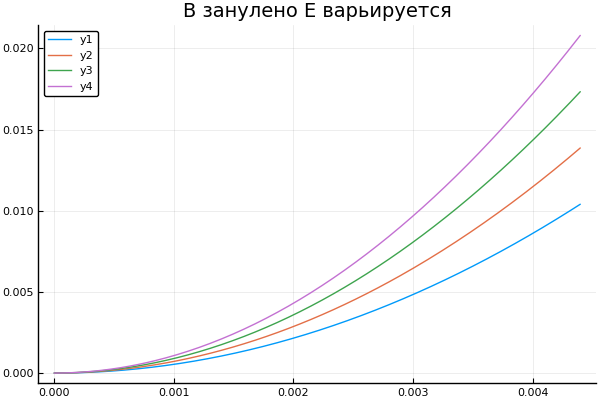
当感应，强度和电荷符号改变时，我们获得粒子的轨迹。让我提醒您，点表示数组的所有元素均按顺序执行函数

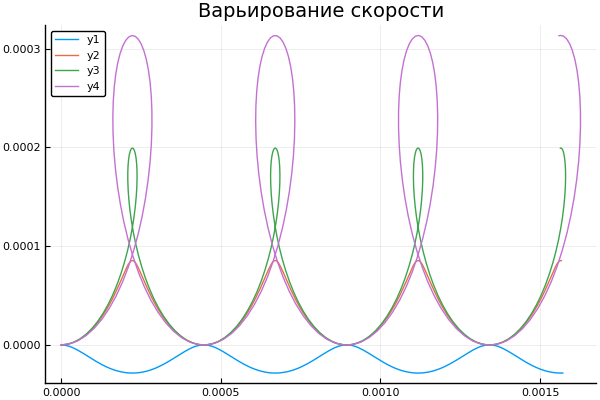
藏起来

 plot() plotter.("B   ", 0, [3e4 4e4 5e4 6e4] )

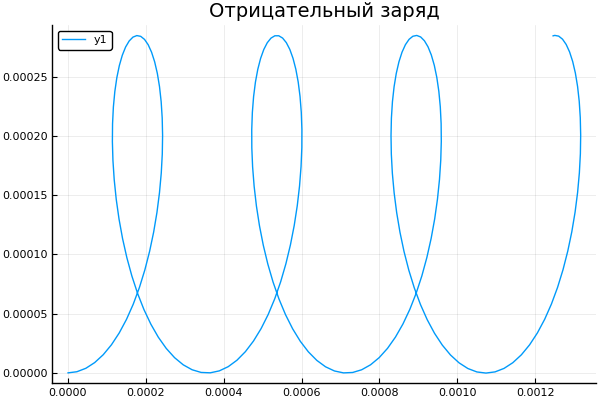
 plot() plotter.("E  B ", [1 2 3 4], 0 )

 q = -1.6e-19 # C plot() plotter.(" ")

让我们看看初始速度的变化如何影响粒子的轨迹：

 plot() plotter.(" ", 2, 5e4, [2e4 4e4 6e4 8e4] )

关于Scilab

在Habré上已经有足够的有关Saylaba的信息，例如1、2 ，以及有关Octave的信息，因此我们将仅限于指向Wikipedia和主页的链接。

我将自己添加一个方便的界面，其中包含复选框，按钮和图形，以及一个非常有趣的Xcos可视化建模工具。后者可用于例如在电气工程中模拟信号：

扰流板

这是一个非常方便的指南：

实际上，我们的任务也可以在Scilab中解决：

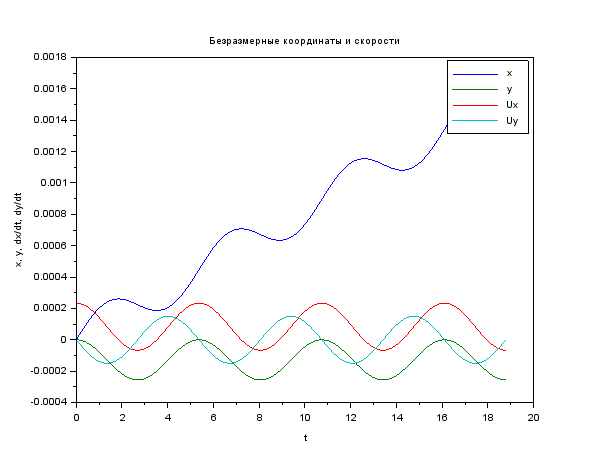
代码和图片

 clear function du = syst(t, u, A, E) du = A * u + [0; 0; 0; E] // ODE system endfunction function [tspan, U] = modelsolver(Bo, Eo, vel) B = Bo*q*lambda / (M*C) E = Eo*q*lambda / (M*C*C) vel = vel / C u0 = [0; 0; vel; 0] // start cond-ns t0 = 0.0 tspan = t0:0.1:6*%pi // time period A = [0 0 1 0; 0 0 0 1; 0 0 0 B; 0 0 -B 0] U = ode("rk", u0, t0, tspan, list(syst, A, E) ) endfunction M = 9.11e-31 // kg q = 1.6e-19 // C C = 3e8 // m/s lambda = 1e-3 // m [cron, Ans1] = modelsolver( 2, 5e4, 7e4 ) plot(cron, Ans1 ) xtitle ("   ","t","x, y, dx/dt, dy/dt"); legend ("x", "y", "Ux", "Uy"); scf(1)//    plot(Ans1(1, :), Ans1(2, :) ) xtitle (" ","x","y"); xs2png(0,'graf1');//       xs2jpg(1,'graf2');// ,  -

这是有关求解极点扩散的函数的信息。原则上，问题是

我们为什么需要朱莉娅？

...如果有Scilab，Octave和Numpy，Scipy这样的奇妙事物？
关于最后两个，我不会说-我还没有尝试过。总的来说，这个问题很复杂，让我们快速看一下：

科学实验室
在硬盘驱动器上，它将占用500 MB以上的内存，它会快速启动，并立即提供差分计算，图形以及其他所有功能。适合初学者：优秀的指南（大多为本地指南），有许多俄语书籍。关于内部错误已经在这里和这里说过，并且由于产品非常小众，因此社区很迟钝，并且额外的模块非常稀缺。

朱莉亚
通过添加软件包（尤其是Jupyter和Mathplotlib中的所有python食物），它的容量从376 MB增长到大约6 GB。她也没有多余的RAM：在132 MB的开始位置，并在Jupiter中绘制了计划后，它会从容地达到1 GB。如果您在Juno中工作，则几乎就像在Scilab中一样 ：您可以在解释器中立即执行代码，可以在内置的记事本中打印并将其保存为文件，并具有变量浏览器，命令日志和在线帮助。就个人而言，我对缺少clear（）感到愤慨，也就是说，我启动了代码，然后开始对其进行更正和重命名，并且保留了旧变量（Jupiter中没有变量浏览器）。

但是，这并不是至关重要的。 Scilab非常适合前几对，制作额头，光标或计算介于两者之间的东西是非常简易的工具。尽管还支持并行计算和调用sishn / Fortran函数，但不能认真使用它。大型阵列使他感到恐惧，要设置多维阵列，您必须处理各种晦涩难懂的问题，而超出传统任务范围的计算可能会使所有内容与操作系统一起掉落。

在经历了所有这些痛苦和失望之后，您也可以安全地切换到朱莉娅（Julia）来这里耙耙。我们将继续学习，社区的利益非常敏感，问题很快得到解决，Julia具有许多有趣的功能，这些功能将使学习过程成为令人兴奋的旅程！

朱莉娅和电磁场中带电粒子的运动

带电粒子在电磁场中的运动

关于Scilab

我们为什么需要朱莉娅？

More articles: