在上一篇文章中，我开始比较了参数优化的方法，即选择参数，评估在随后的回测期间交易机器人的盈利能力。事实证明，普通的蒙特卡洛方法-生成机器人参数的随机不相关的组合-效果很好。现在，我想测试一种流行的算法，其中包括编程商人社区中的一种：遗传优化算法。

用于优化交易策略的遗传算法

我们将以该算法为例来优化2个参数。我们的机器人的优化参数是移动平均周期和TakeProfit 。为了更深入地了解“遗传”，让我们同意将移动平均线的周期称为负责“增长”的基因，将TakeProfit称为“眼睛颜色”的基因。

在允许的参数值空间内，每个点，每对坐标-“高度/眼睛颜色”理论上都描述一个“个体”。假设我们随机创建了10个人。这是遗传优化算法的第一步 -创建第一代：

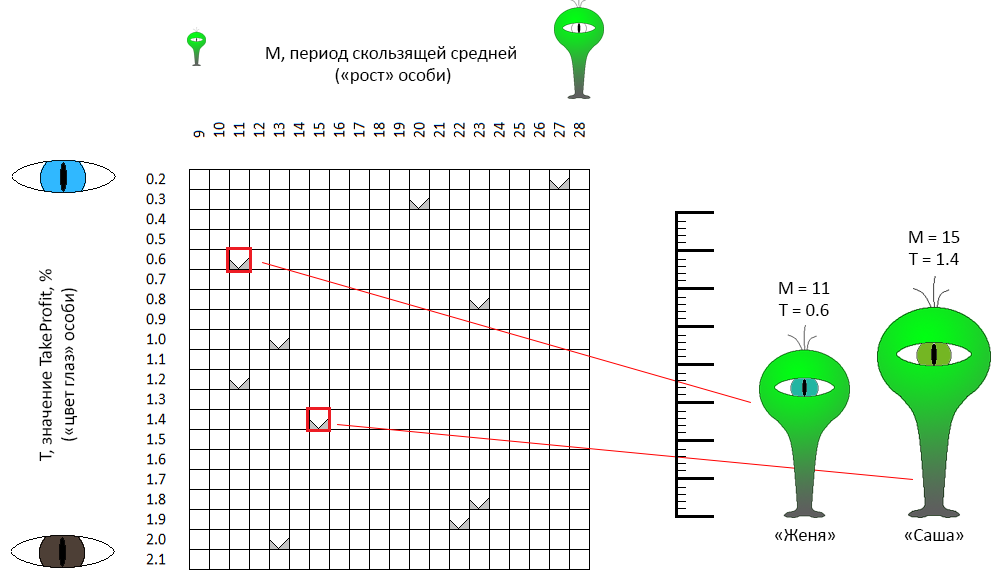
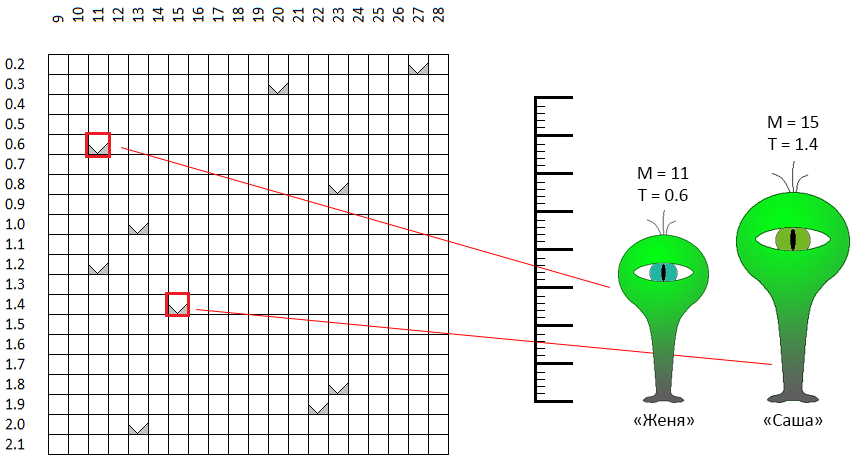
在坐标空间M-T中，随机选择点。例如，两个标有红色框的点是具有性别中立名称的“个人”（这很重要！），Zhenya和Sasha。 Sasha的“增长”（问题的最初公式是移动平均周期）为11个单位，“眼睛颜色”为0.6（绿蓝色的眼睛）。振亚的参数略有不同。相同的特征描述了剩下的8个人。

第二步是繁殖

从整个第一代开始，我们确定一定数量的“最成功”个人。显然，该标准是CF的值。这些个体将繁殖，随机配对（因此，他们获得了性别中立的名字）。通常，可以为匹配对设置许多规则。例如，要选择特征上最接近个体（即，字面上在坐标空间上最接近）的个体-近交。相反，您可以寻找对立（近亲繁殖）。我找不到支持这些选项之一的论据-在我的实现中，这对是严格由偶然形成的。例如，Zhenya和Sasha通过了资格认证并决定生下后代。在我们的上下文中这意味着什么：

从两个“父母”个体中，我们获得了第三个个体，该个体继承了一个父母的一部分特征，另一个父母的一部分特征。例如，Zhenya和Sasha生了一个个人Nikita（Nikita，Nikita？）：

Nikita从他的父母之一“ Zhenya”那里继承了“眼睛颜色”（机器人的TakeProfit参数）符号，
Nikita的“成长”（移动平均机器人的时期）是从“ Sasha”继承而来的，但是在另一位父辈Zhenya的方向上做了一些调整。

事实是，优化空间的尺寸越小（在我们的示例中等于2），后代将“越接近”。遗传优化算法并未严格确定子孙个体基因“遗传”的规则。因此，尼基塔随机地借用了他的眼睛的颜色，没有任何变化，但事实证明他是在父母双方之间的中间，更靠近父母中的一个。在我的实施中，同样成功，Nikita可以从父母双方那里借用原始参数。

第三步是繁殖

进化过程的推手，自然选择。 10个最好的人中有4个给出了10个后代。现在我们有20个人。遗传优化算法涉及维持恒定的种群规模。 10个人必须“死亡”。在此实现中，第一代的大多数人“死亡”，从80％到100％。
因此，在我们的示例中，新一代将由0 ... 2个父母及其8-10个后代组成。换句话说，如果您省略歌词，那么交易机器人参数的新向量将根据上一步中的4个最佳测试的“传播”（组合）来计算。大多数“老人”将不接受参与新的选择迭代（可能有其他实现选择的选项）。

算法完成

复制和选择重复N次。具体而言，在我们的示例中，为了与之前测试的三种算法进行比较，测试了10个体的4代，共40项测试。
但是，可能会发生另一个人口崩溃的情况。换句话说，所有测试都将在几个点附近。为了避免这种情况，使用了几种机制，特别是：

向人群中注入“新鲜血液”。在当前人口的后代中，以偶然的方式添加了几个新个体，形成初始人口的方式相同，
变异机制：后代个体的某些特征（坐标）可能与其父母的特征略有不同：

在这个例子中

简和乔斯的后代的特征-“成长”和“眼睛的颜色”是从每个父母那里借来的，
Sam和Siri的后代特征与父母双方的相应特征有些不同。

在我的实现中，尽管存在突变和“新鲜的个体”，但总体上还是必须定期更新总体，以避免过早收敛，将整个群体定位在有限的空间内。

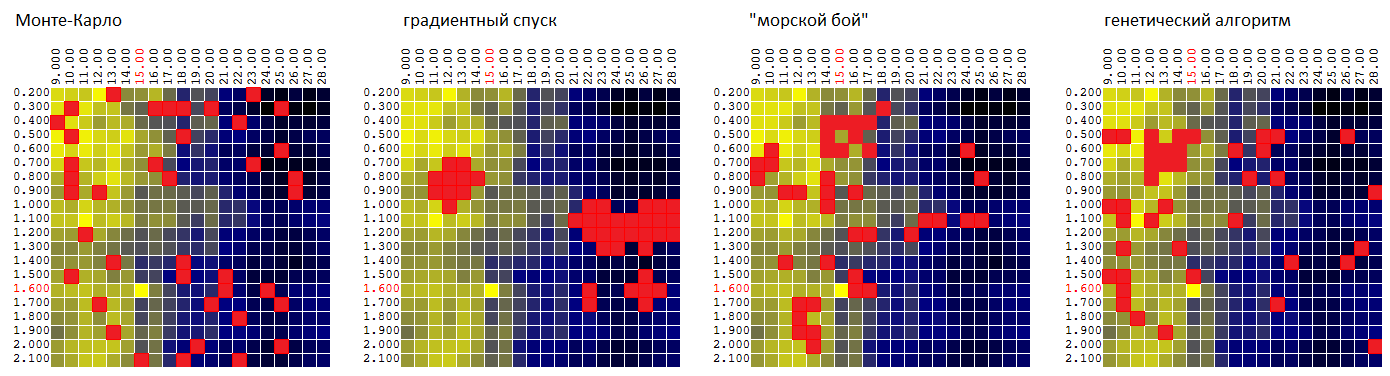
如果返回到测试蒙特卡洛算法，梯度下降以及工作名称为“ sea Battle”的算法的原始数据，则优化过程可以通过以下动画说明：

从动画中可以看到，起初，点的排列是混乱的，但在随后的世代中，往往会出现具有较高DF值的区域。

现在比较同一表面上的算法： P = f（ M ， T ）：

蒙特卡洛	梯度下降	“海战”	遗传算法
95.7％	92.1％	97.0％	96.8％

求出的CF极值的平均值占总值的百分比。

当然，用一组输入数据来判断还为时过早，但是到目前为止，就我们的交易机器人而言，遗传算法不如“海战”算法：

相当微不足道-通过找到的CF的准最佳值的平均值，
给出了交易算法的参数稳定性的最差估计，因为它没有“调查”过于详细的准最优参数元组的周围环境。

四种优化算法的最终测试

最终测试是对4组输入数据进行的-交易策略在价格历史记录的4个不同部分上的回测结果（ EURUSD ：2016，EURUSD：2017， XAUUSD ：2016，XAUUSD：2017）。

（数字过滤器作为4个时间序列价格的两个参数的函数的示例）

这次，根据3个参数进行了优化：

“快速”移动平均线的时期
缓慢的移动平均线
TakeProfit（交易利润，以百分比表示，达到交易完成时的百分比）。

每个参数取20个不同的值。共建表
P = F（Mf，Ms，T）
其中P是利润，Mf是“快速”移动平均线的周期，Ms是“慢速”移动平均线的周期，T是TakeProfit，
20 * 20 * 20 = 8,000次测试迭代。

在160、400和800个测试（所选坐标中的DF计算）的限制下进行了优化。每次，将结果平均1,000次优化迭代。找到的拟最佳参数向量的平均DF值为：

蒙特卡洛	梯度下降	“海战”	遗传算法
84.1％	83.9％	77.0％	92.6％

另外，值得注意的是，即使在选项总数中的一小部分测试中，GA仍显示出良好的结果：

测试	蒙特卡洛	梯度下降	“海战”	遗传算法
8,000分之160	79.1％	76.7％	73.1％	87.7％
8,000分之400	84.7％	85.0％	77.4％	93.7％
8,000中的800	88.6％	90.1％	80.4％	96.3％

而不是结论

结果显示了遗传优化算法，令我有些惊讶。我认为该方法的“遗传范式”没有将他排在第一位。从某种意义上说，根据坐标选择的逻辑，它类似于二分法/黄金分割法。可能值得尝试这些算法之一，并将GA与之比较。

回到交易机器人，值得注意的是，CF（利润）形成的表面“浮雕”每年都在变化。也就是说，在2017年的历史上“优化”了机器人， 在2018年 （第一季度，月份，周... 2018年） 应用这些设置是没有意义的 。

像我们这样的人工，教条和无助交易策略（在移动均线的交点处购买）可能不会很快过时。不幸的是，我没有其他任何策略。因此，我将交易机器人的收益或损失归因于运气，而不是算法的优缺点。因此，对我而言，交易机器人的参数优化任务对我个人而言完全是学术兴趣。

优化交易机器人：遗传算法