在许多任务中，将长时间信号划分为多个部分，每个部分分别进行处理。 特别地，在合成过程中，该方法用于使用窗口傅立叶变换来分析信号，反之亦然。 以及频谱处理，例如噪声消除，速度变化，非线性滤波，音频数据压缩等。

分区本身的过程在数学上通过乘以具有偏移量的某些权重（ 窗口 ）函数来表示。 对于最简单的窗口-矩形-可能看起来像这样：

源信号：



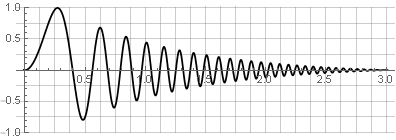
分区：







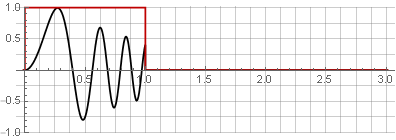
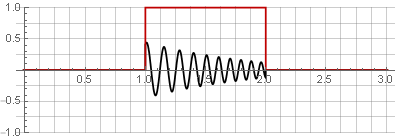
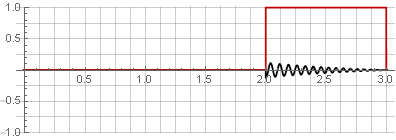
您可以通过简单地将它们相加来恢复原始信号。

更多细节

但是通过 由于多种原因，矩形函数不是最佳的窗口函数。 在频谱分析中，通过（通常是快速的）离散傅立叶变换，被分析的数据块似乎是“循环”的，这会导致边缘出现间隙并导致频谱失真：



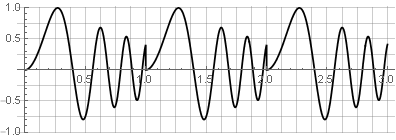
它也不适合进行逆向合成-因为任何更改都会导致中断-例如，如果我们尝试逆转其中一个部分：



为了消除这些缺点，使用了重叠-当每个随后的窗口捕获前一个窗口的部分数据时； 和权重窗口分别逐渐下降到边缘。

重叠50％

大多数情况下，他们使用Hannah窗口 （也称为“升余弦”），且重叠率为50％：








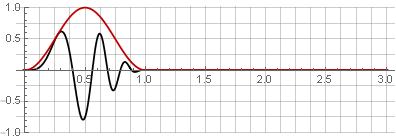
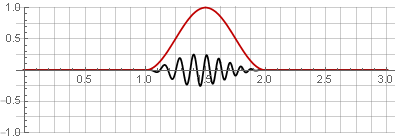
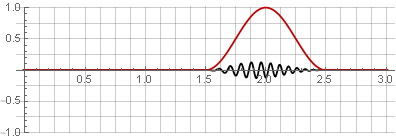
由于加法期间余弦函数的对称性，它们被求和为单位：



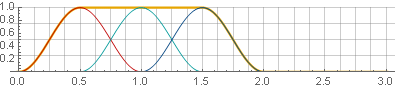
现在，通过逆向综合，我们将不会获得间隙-只是在窗口边界的值仍将为零的情况下。 例如，当反转零件之一时，不会破坏光滑度：

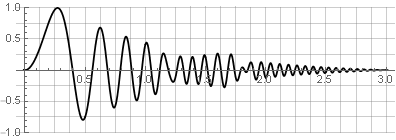
双覆盖处理

更详细地考虑使用快速傅里叶变换（FFT）处理信号的算法：

1. 用窗口覆盖将信号分成多个部分；
2. 直接FFT;
3. 频谱处理；
4. 逆FFT
5. 重复的窗口覆盖（因为在反向FFT之后，边界不一定会停靠为零而不中断）；
6. 结果段的总和。

此外，如果不执行频谱处理，则输出信号应与输入信号相同（仅具有不可避免的时间延迟）。

使用Hann窗口时，重叠50％不再足够，因为会出现倾斜：



由于双重重叠等于平方，所以显而易见的解决方案是使用Hann窗口的根来补偿平方：



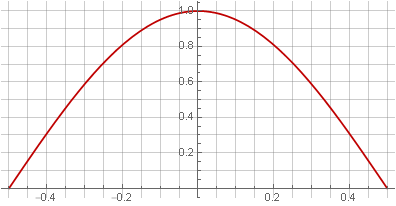
但是，在这种情况下，窗口的边缘不再平滑-一阶导数中出现了间隙。


您可以采用另一种方法-使用75％的重叠量，然后窗口也将被累加为一个常数-仅在 $$$1$ 和 $$$\ frac {3} {2}$ ：



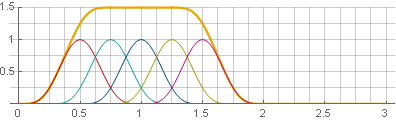
在这种情况下，我们很幸运。 如果将平方扩展为总和，则可以看到它是两个汉娜窗口的组合，但是比例不同，这使我们能够满足所需的要求：

$$

$$\左（\ frac {\ cos（2 \ pi x）+1} {2} \右）^ 2 = \ frac {\ cos（2 \ pi x）+1} {2} + \ frac {\ cos （4 \ pi x）-1} {8}$$

对于其他窗口功能，这种技巧将不起作用。 同样，即使在50％重叠时，并非所有标准窗口函数都可以提供恒定的求和。

主意

我们可以将Hann窗口视为一个独立函数，而不是两个分段的连续函数之间的差异（ 单独的文章专门讨论了它们），但有一个偏移量。 例如，使用以下功能

$$

$$\ left \ {\ begin {array} {ll} -1＆x \ leqslant -1 \\ 1＆x \ geqslant 1 \\ \ sin \ left（\ frac {\ pi x} {2} \ right）＆ -1 <x <1 \\ \ end {array} \对$$

可以写

$$

$$f（x +1）-f（x-1）$$

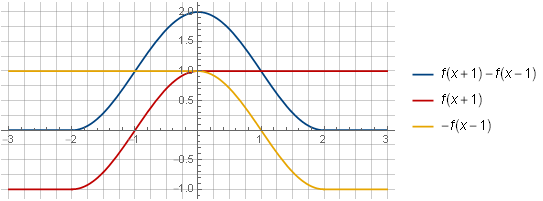
考虑了两个这样的窗口之和的组成部分之后，它们总结成一个常数的能力将变得更加直观：



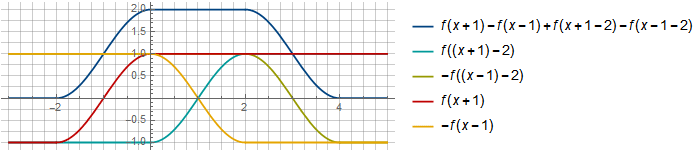
在细分市场上 $$$[0,2]$ 我们除了功能外还获得了相互补偿 $$$-f（x-1）$ 和 $$$f（（x + 1）-2）$ 从 $$$f（（x + 1）-2）= f（x-1）$

您可以选择另一个具有更多重叠的偏移量，例如：

$$

$$f \左（x + \ frac {1} {2} \右）-f \左（x- \ frac {1} {2} \右）$$

然后，逐步移动时 $$$\ frac {1} {2}$ ，它们也将被汇总为一个常数：



可以看出，如果重新安排窗口功能的组件，则会得到相同的Hann窗口。

因此，使用不同的限制功能，可以形成所需形状的窗口。

最终配方

现在仅需设置比例尺，以使定义区域和值不依赖于重叠值。 在间隔上定义窗口 $$$[0,1]$ 我们得到

$$

$$\ frac {f \ left（\ frac {2 tx} {t-1} -1 \ right）-f \ left（\ frac {2 t（x-1）} {t-1} +1 \ right） } {2}$$

在哪里 $$$f$ -形式的分段连续函数

$$

$$\ left \ {\ begin {array} {ll} -1＆x \ leqslant -1 \\ 1＆x \ geqslant 1 \\ g（x）＆-1 <x <1 \\ \ end {array} \是的$$

但是 $$$g$ -点之间的一些插值功能 $$$（-1，-1）$ 和 $$$（1,1）$ 。

参量 $$$t$ 确定重叠程度-一个分隔符，确定每个下一个窗口必须移动的步长， $$$x_ {n + 1} = x_n + \ frac {1} {t}$ ，并且必须大于1， $$$t> 1$ 。

重叠百分比 $$$p$ 可以通过公式计算

$$

$$p = \ frac {100（t-1）} {t}$$

反之亦然

$$

$$t = \ frac {100} {100-p}$$

窗口的最终外观将取决于重叠级别的选择和限制功能的选择。

一些有趣的例子

在这里，我们将看一些现成的解决方案，一切都已开始。 为简单起见，我们考虑一个简单的插值函数 $$$g（x）$ ，没有其他捆扎。

多项式窗口

它们在计算上最便宜。 使用先前导出的公式

$$

$$\ frac {2 x \ Gamma \ left（n + \ frac {1} {2} \ right）\，_2F_1 \ left（\ frac {1} {2}，1-n; \ frac {3} {2} ; x ^ 2 \ right）} {\ sqrt {\ pi} \ Gamma（n）}$$

我们在较高的导数上获得给定数量的零的多项式，该多项式可为边缘提供必要的窗口平滑度。


如果窗口的重叠率为75％，且n的值不同，则窗口将如下所示：



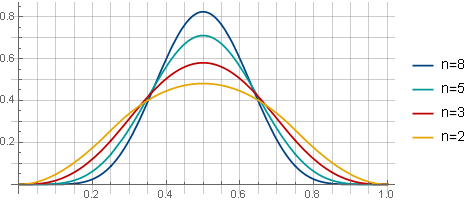
并且对于根提取-这样（当使用75％重叠时）：



左右（使用50％重叠时）：

最平滑的窗口

功能介绍

$$

$$\ tanh \ left（\ frac {k x} {\ sqrt {1-x ^ 2}} \ right）$$

有趣的是，它是无限可微的，并且其边缘的所有导数均为0（可以通过根据微分规则考虑其导数来证明-每个项中都有一个零因子）。 这使我们能够在其基础上构建窗口，所有窗口均无间隙：

窗口视图“裙子”

对此类窗口的需求是由于提高了FFT分辨率，但通过增加其在中央的集中度来降低高频下“时频不确定性”效应的影响。

首先，我们确定所需的窗口函数类型-例如，如下所示：

$$

$$-\日志\左（k ^ 2 x ^ 2 +1 \右）+ \日志\左（k ^ 2 +1 \右）-\ frac {k ^ 2 \左（1-x ^ 2 \右） } {k ^ 2 + 1}$$

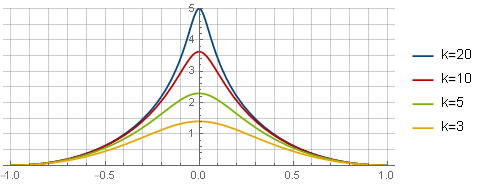
在这里，第一项决定函数本身的形式，第二项-提供与横坐标轴的交点，第三项（抛物线）重置边缘处的导数以平滑对接； 和参数 $$$k$ 定义峰的“清晰度”。 这种形式尚不适合使用-首先，您需要通过集成和缩放从限制函数中获取限制功能：

$$

$$\ frac {kx \左（k ^ 2 \左（x ^ 2 + 3 \右）+6 \右）+3 \左（k ^ 2 +1 \右）\左（kx \左（\ log \左（k ^ 2 +1 \右）-\日志\左（k ^ 2 x ^ 2 +1 \右）\右）-2 \ tan ^ {-1}（kx）\右）} {4 k ^ 3-6 \左（k ^ 2 + 1 \右）\ tan ^ {-1}（k）+6 k}$$

为了方便起见，您可以绑定参数 $$$k$ 达到重叠的水平 $$$t$ -例如，使窗口中心的四阶导数为0-然后 $$$k$ 将被视为 $$$\ sqrt {3}（t-1）$ ：



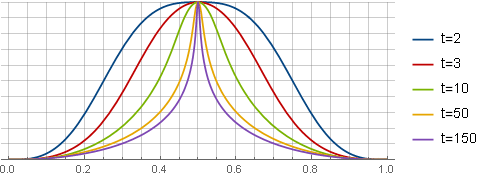
在这里，为清楚起见，所有窗口都缩小到相同的比例。

针查看窗口

它是上一个窗口的更“激进”版本。 选择了一个夸张的基础，然后通过连续变换

$$

$$\ frac {1} {x} \到\ frac {1} {\ sqrt {x ^ 2}} \到\ frac {1} {\ sqrt {x ^ 2 + 1}} \ to \ frac {1} {\ sqrt {k ^ 2 x ^ 2 + 1}} \到\ frac {\左（1-x ^ 2 \ right）^ 2} {\ sqrt {k ^ 2 x ^ 2 + 1}}$$

并使用积分和缩放形式的相同步骤得出公式

$$

$$\ frac {kx \左（2 k ^ 2 \左（x ^ 2-4 \右）-3 \右）\ sqrt {k ^ 2 x ^ 2 +1} + \左（8 \左（k ^ 4 + k ^ 2 \右）+3 \右）\ sinh ^ {-1}（kx）} {\左（8 \左（k ^ 4 + k ^ 2 \右）+3 \右）\ sinh ^ {-1}（k）-3 k \ sqrt {k ^ 2 + 1} \左（2 k ^ 2 + 1 \右）}$$

在这里您还可以绑定参数 $$$k$ 达到重叠的水平。 四阶导数方程的直接解给出了一个繁琐的结果，因此只需通过定义 $$$k$ 怎么 $$$k（t-1）$ 从而确保参数的作用 $$$k$ 作为“微调”。 在 $$$k = 2.22$ Windows将如下所示：

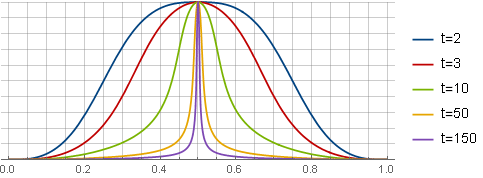
不对称窗口

窗口函数完全不必对称。 假设我们需要一个具有尖锐攻击力和平滑衰减的窗口。 我们可以根据已经熟悉的方案来获得它-首先确定函数的期望形式，然后通过集成获得约束函数。 由于非对称性，中心将不再通过原点，因此该任务稍微复杂一些，因此添加了额外的计算步骤。 这也导致这样的事实，即公式相当麻烦。 例如，考虑最简单的选项-抛物线乘以多项式权重窗口：

$$

$$（1-x）^ 2 \左（1-x ^ {10} \右）^ 2$$

在此，加权窗口中的x程度（即10）决定了攻击的“清晰度”。 为了清楚起见，我们使用一个特定的值而不是一个符号参数来简化公式-如果您愿意，可以稍后重新计算。

集成后，仅缩放已不再足够-您仍然需要对齐边缘：



为此，我们首先将函数上移以对齐左边缘，然后将其缩放到右边缘的两个并减去一个。 然后我们得到以下公式：

$$

$$\ frac {8775 \ left（\ frac {x ^ {27}} {27}-\ frac {2 x ^ {26}} {26} + \ frac {x ^ {25}} {25}-\ frac {2 x ^ {15}} {15} + \ frac {4 x ^ {14}} {14}-\ frac {2 x ^ {13}} {13} + \ frac {x ^ 3} {3} -x ^ 2 + x + \ frac {117592} {61425} \ right）} {9856} -1$$

为了使最终的窗口具有所需的外观，还必须提供足够大的重叠度：

结论

同样，您可以从其他任何钟形函数（例如，高斯函数）构建窗口。 您还可以修改那些已经考虑过的参数，以提供更大的平滑度或更改曲线的形状。

不考虑这些窗口函数的频谱组成，应单独进行研究。

可以在此处下载Wolfram Mathematica文档形式的文章的稍微高级的版本（具有在考虑中的窗口和隐藏的公式中动态更改参数的能力）。