您需要多少程序员来支持以前编写的代码？

前段时间，我和我的好朋友之间进行了一次对话，其中听起来有些话：

-程序员的数量将不断增长-因为代码量在不断增长，并且越来越需要越来越多的开发人员来支持它。
-但是代码正在老化，部分代码已不再支持。 不排除某种平衡的存在。

几天后回想起它们，我想知道随着时间的推移需要越来越多的资源的代码支持是否会最终使新功能的开发瘫痪，或者需要无限增加程序员数量？ 数学分析和微分方程有助于定性评估支持量对发展的依赖性并找到问题的答案。

第一个问题。 可以支持“吞噬”所有开发资源吗？

考虑一个由人数恒定的程序员组成的团队。 他们的工作时间份额 $$$\亩（t）$ （ $$$0 <\亩（t）<1$ ）占开发新代码的时间，其余时间占比 $$$1- \亩（t）$ 去支持。 在模型的假设下，我们假设第一种活动旨在增加代码量，第二种活动旨在改变代码量（纠正错误）并且不会显着影响代码量。

我们表示 $$$y（t）$ 所有按时间编写的代码 $$$t$ 。 考虑到编写代码的速度成正比 $$$\亩（t）$ 我们得到：

$$

$$\ frac {dy（t）} {dt} = a_0 \ mu（t）; a_0 \ in \ mathbb {R}，a_0> 0$$

很自然地认为，维护代码所涉及的劳动与代码量成正比：

$$

$$1- \ mu（t）= a_1 y（t）; a_1 \ in \ mathbb {R}，a_1> 0$$

或

$$

$$\亩（t）= 1-a_1y（t）$$

从哪里来

$$

$$\ frac {dy（t）} {dt} = a_0（1-a_1y（t）））$$

我们得到一个易于积分的微分方程。 如果在初始时间代码量为零，则

$$

$$y（t）= \ frac {1} {a_1}（1-e ^ {-a_0a_1t}）$$

在 $$$t \到+ \ infty$ 机能 $$$y（t）\ to1 / a_1$ 和 $$$\亩（t）\至0$ 。 这就意味着随着时间的流逝，新功能的开发将逐渐减少为零，并且所有支持的资源都将转移。

但是，如果及时 $$$h> 0$ 由于代码已过时并不再受支持，因此一次需要支持的代码量 $$$t$ 等于 $$$y（t）-y（t-h）$ 然后

$$

$$1- \ mu（t）= a_1（y（t）-y（t-h）），$$

$$

$$\ mu（t）= 1-a_1（y（t）-y（t-h）），$$

但是 $$$y（t）$ 是具有延迟参数[1]的微分方程的解：

$$

$$\ frac {dy（t）} {dt} = a_0（1-a_1（y（t）-y（t-h）））$$

通过设置值唯一确定此方程式的解 $$$y（t）$ “在时间开始之前”， $$$t \ in [-h，0]$ 。 由于在初始时间之前没有编写任何代码，因此在我们的情况下 $$$y（t）= 0$ 在 $$$t \ in [-h，0]$ 。

让我们看几个例子。 我们将以年为单位来度量时间，以数千行来度量代码量。 然后 $$$a_0$ 几十个数量级的值是可以接受的，我们取50和100。也就是说，开发团队一年将分别编写五十和十万行代码。 对于 $$$a_1$ 可接受的值可能是： $$$0.25 / a_0$ ， $$$0.5 / a_0$ ， $$$1 / a_0$ 。 这意味着开发团队能够以四分之一，一半或全部的工作量来维护其当年编写的代码量。 作为代码的平均寿命，让我们设置以下值：1、2和4年。 通过数值求解方程，我们获得了函数行为的示例 $$$\亩（t）$ 对于某些参数组合 $$$h，a_0，a_1$ 。

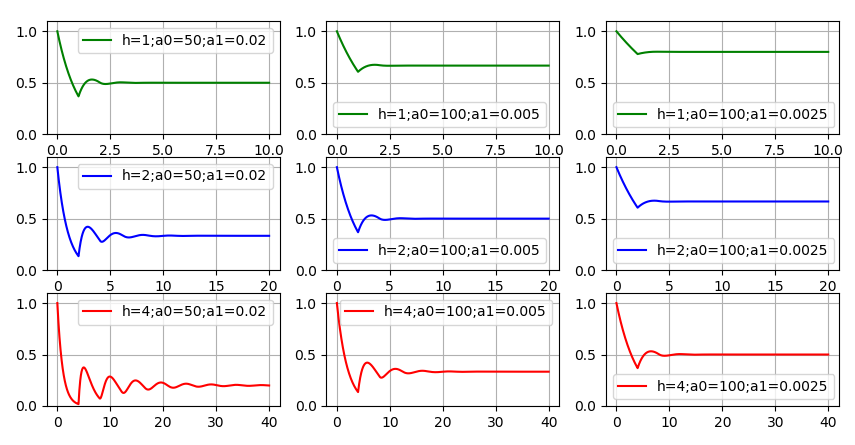
功能行为 $$$\亩（t）$ 面对老化的代码已经改变。 该功能已不再单调，但随着时间的流逝“平静下来”，有一种趋向于 $$$\亩（t）$ 保持恒定 图表显示：更多 $$$h$ ， $$$a_0$ 和 $$$a_1$ ，也就是说，代码变旧的速度越慢，新代码的开发就会越快，并且代码的质量越低，用于开发新功能的资源将更少。 希望至少举一个例子， $$$\亩（t）$ “走私”接近零。 但这需要选择非常差的开发质量指标和长期代码。 即使在左下方的图表中，新功能仍会占用大量资源。 因此，第一个问题的正确答案很可能是这样的：理论上-是的，这是可能的； 实际上-几乎没有。

无法回答的问题：

1. 是真的吗 $$$\亩（t）$ 倾向于 $$$t \到+ \ infty$ 对于所有 $$$a_0，a_1> 0$ ？ 如果不是每个人都适合的话？
2. 如果存在限制，那么其值如何依赖 $$$a_0，a_1$ ？

第二个问题。 代码支持能否引起程序员数量的无限增长？

我们表示 $$$q（t）$ 参与新代码开发的程序员数量。 如上 $$$y（t）$ -当时编写的代码量 $$$t$ 。 然后

$$

$$\ frac {dy（t）} {dt} = a_2 q（t）; a_2 \ in \ mathbb {R}，a_2> 0$$

让代码支持忙 $$$p（t）$ 程序员。 C代码老化

$$

$$p（t）= a_3（y（t）-y（t-h））; a_3 \ in \ mathbb {R}，a_3> 0$$

从哪里来

$$

$$p（t）= a_3 \ int_ {t-h} ^ {t} \ frac {dy（s）} {ds} ds = a_2a_3 \ int_ {t-h} ^ tq（s）ds。$$

如果 $$$q（t）\ leq C_1$ 然后

$$

$$p（t）\ leq a_1a_2C_1h$$

因此，第二个问题的答案是否定的：如果新代码的开发人员数量有限，那么在代码老化的情况下，支持不能导致程序员数量的无限增加。

结论

所考虑的模型是“软”数学模型[2]。 他们很简单。 尽管如此，仿真结果对参数值的依赖性与实际系统所期望的相符；这表明模型的充分性和足够的准确性以获得定性估计。

参考文献

1. Elsgolts L.E.，Norkin S.B. 具有偏差参数的微分方程理论简介。 莫斯科 出版社《科学》。 1971年。
2.阿诺德五世 “硬”和“软”数学模型。 莫斯科 中心出版社。 2004。