新的统计模型似乎破坏了数论早已接受的假设。 如果只有严格的证据确实重要,您可以信任她多少?
椭圆曲线y 2 = x 3-4x +1上的哪些点是有理的? 要找到它们,您需要通过成对的有理点画线。 线通过的所有点也是合理的。最近,有四位研究人员提出了一个模型,该模型颠倒了他们研究领域的整体常识。 他们使用计算数据表明,几十年来对基本概念之一的普遍看法是错误的。
这些不是生物学家,气候学家或物理学家。 在他们的科学领域中,经验模型没有关于真理的发言权。 他们是数学家,是该学科的代表,他们的标准货币(不可否认的逻辑证明)通常使他们免于影响其他领域的辩论。 然而,他们来了,他们的模型说可能是时候修改一些长期存在的想法了。
一个在2016年
在线发布并准备出现在《欧洲数学学会杂志》上的模型属于一个古老的数学概念,如代数方程组的等级。 等级是一种度量,它对应于方程的多少解与有理数有关,哪些与无理数有关。 高阶方程具有更合理的解并且更复杂。
从20世纪初开始,数学家一直对方程式行列的高度是否受到限制的问题感兴趣。 最初,几乎每个人都认为应该存在限制。 但是到1970年代,主流观点已经改变-大多数数学家开始相信秩是无限的,这意味着可以检测到具有无限大秩的曲线。 事情发生了,尽管一些数学家认为没有强有力的论据支持这一观点。
“人们对没有限制感到非常专制。 但是,当您开始理解时,事实证明,这样做的证据非常薄弱,”蒙特利尔大学和伦敦大学学院的数学家
安德鲁·格兰维尔说。
如今,证据表明情况并非如此。 模型出现两年后,她说服了许多数学家,某种类型的代数方程组的等级确实受到限制。 但是,并非所有人都认为这种模式令人信服。 缺乏共识提出了与数学结果通常不相关的问题-在仅严格证明很重要的领域中,经验证据可以发挥多大的作用?
这项工作的共同作者,俄亥俄州大学的数学家
詹妮弗·帕克 (
Jennifer Park)说:“没有数学上的理由证明这种模型正是我们所需要的。” “此外,从实验的角度来看,很多事情都起作用。”
点对点
如果给定方程式,则可以在图形上绘制其解的曲线。 数学家想知道这些解决方案中有多少是合理的-它们属于数字类型,可以表示为两个整数的比率(1/2,-3或4483/929)。
理性的解决方案很难系统地找到,但是数学家拥有的技术可以在特定条件下运行。 取方程x
2 + y
2 =1。该方程的解图是一个圆。 为了找到圆的所有有理点,我们从一个确定的解决方案开始-假设从x = 1和y = 0的点开始。 然后在此点上画一条线,在另一点与圆相交。 如果我们的线的斜率是合理的,那么第二个交点也将是合理的解决方案。 通过画一条线,我们将理性决策的数量从一个增加到了两个。
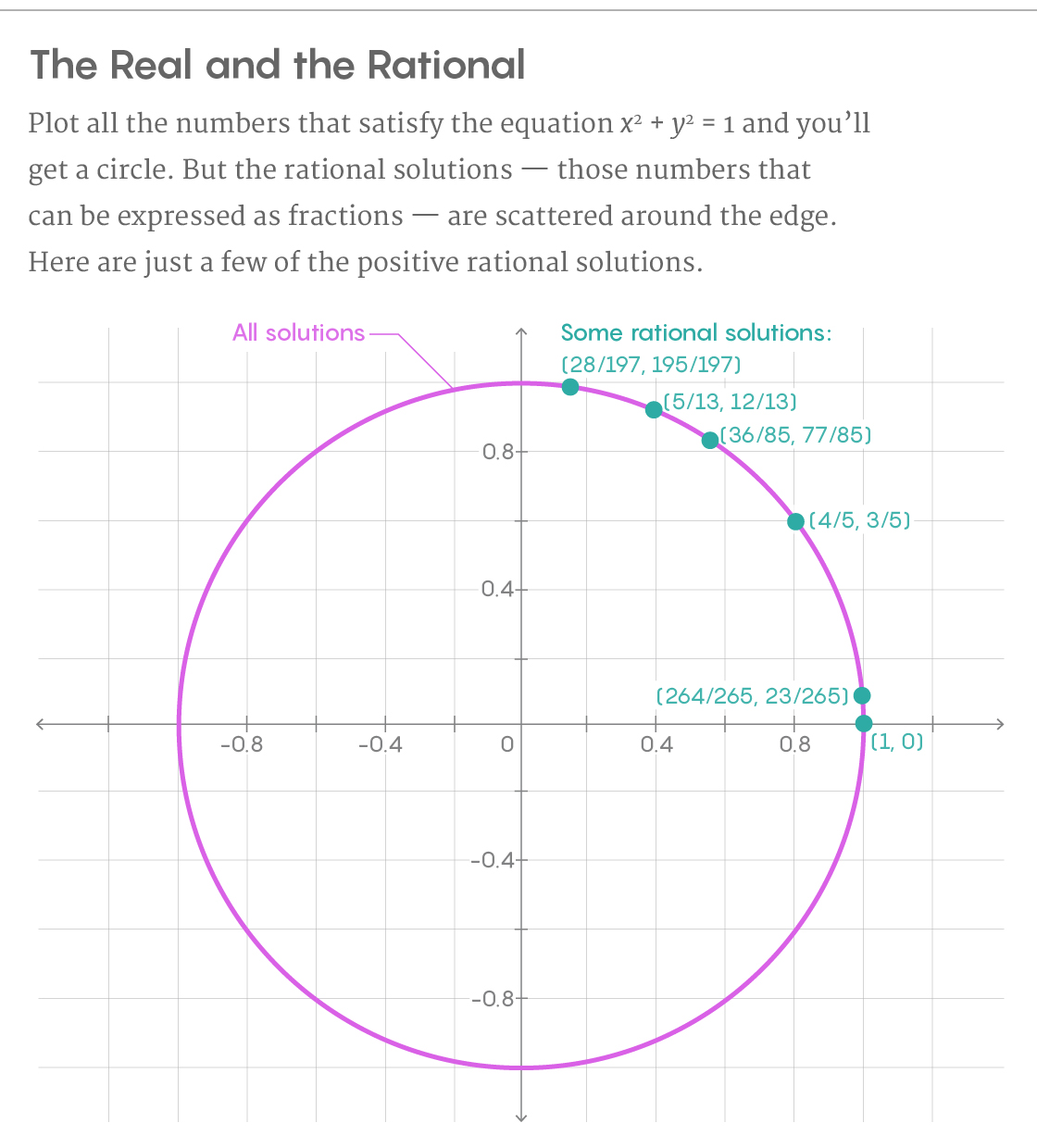
而且没有必要停在那里。 我们通过在第二个有理点上绘制一条与另一个有理斜率的直线来重复该过程-它在第三个有理点处与圆相交。 继续这种方式到无穷大,我们最终将找到圆的所有有理点,其中有无限个。
如果是圆形,则只需从一个点开始,就可以找到所有点。 为了找到所有其他决定而需要在开始时知道的理性决定的数量称为曲线的等级。 等级是用单个数字描述无限的理性决策的一种巧妙方法。 麻省理工学院的数学家,该模型的合著者,麻省理工学院的数学家
比约恩·普南(BjörnPuunen)与帕克,达特茅斯学院的
约翰·沃伊特和威斯康星大学的
梅兰妮·马修·伍德说:“这就像是描述这些曲线的合理解的最佳方法。”
圆是二次方程,或者是第二度的方程(“度”是指方程项中最大的度的大小)。 一百多年来,数学家们知道如何找到二阶方程的有理解。
下一类方程式是椭圆曲线,其中变量升至三次。 椭圆曲线存在于最吸引人的数学研究领域。 它们比二阶方程更复杂,因此它们很有趣,但是并不太复杂。 更改的绘制直线的过程仍然适用于椭圆曲线,但不再适用于四阶或更高阶的方程。
椭圆曲线的等级不同。 对于某些椭圆曲线,您可以从一个有理点开始,应用绘制线的过程,而不能找到所有有理解。 您可能需要添加与第一点不相关的第二个有理点。 有了它,您将开始绘制线的新过程,并且可以找到有理点的平衡。 要找到所有需要首先了解两个有理点的有理点的曲线,其等级等于2。
没有证明对椭圆曲线的秩的高度有限制。 等式的等级越高,曲线的有理解集越宽且越复杂。 Puunen说:“等级以某种方式衡量了决策的复杂性。”
尽管如此,该排名仍未涵盖数学家在理论上对其进行描述的尝试。 如果给定椭圆曲线,则它的外观与等级之间不会有明显的关系。 帕克说:“如果我有一条椭圆曲线,而我稍微调整系数,那么它的等级就会发生根本变化。” -您可以将系数更改为一,排名将跃升至一百万。 没有人知道军衔如何。”
缺乏通用理论导致数学家撤回了他们为推测等级限制的存在而提供的少量证据。 格兰维尔说:“观点是,对职级没有限制,因为人们一直都在寻找越来越高的职级。” 当前的记录保持者是第28级的椭圆曲线,该曲线由哈佛大学的数学家Noam Elkis于2006年发现。
但是后来出现了这个新模型,并说这几乎可以肯定这条路的尽头。
21点左右惊喜
为了研究太复杂或无法直接研究的现象,科学家使用模型。 在实验室中创建了黑洞的类似物之后,他们可能无需沿事件视界的边缘就可以学习有关真实黑洞行为的一些信息。
数学家也这样做。 素数的研究就是一个很好的例子。 数学家想知道有关
双素数的问题的答案-是否存在无数对相差2(3和5、11和13)的素数。 详尽的答案超出了他们的知识范围,但是他们创建了预测孪生数出现频率的模型-答案似乎是它们发生了无数次。
新模型不会直接研究椭圆曲线本身。 她探索诸如
矩阵核这样的数学对象。 原子核指的是椭圆曲线,就像老鼠对人不是一回事,但它们更易于研究,希望它们足够接近,可以根据对其他动物的实验得出一些结论。 特别是,内核具有自己的
rank版本。 在研究了原子核的秩的分布(多少个核的秩为1,多少个核的秩为2等等)之后,四位数学家希望对椭圆曲线的秩的分布有所了解。 实际上,他们打赌核和椭圆曲线的秩分布彼此相似。
 珍妮佛公园(Jennifer Park),比约恩·普南(Bjorn Puunen)和梅兰妮·伍德(Melanie Wood)
珍妮佛公园(Jennifer Park),比约恩·普南(Bjorn Puunen)和梅兰妮·伍德(Melanie Wood)帕克说:“信念的飞跃发挥了作用。” “我们希望也许还有另一组数学对象更容易理解,并且具有与椭圆曲线相同的秩分布。”
当四位研究人员完成这项工作时,大多数数学家都认为排名不受限制。 但是,模型讲述了一个不同的故事。 她说,只有数量有限的椭圆曲线,其秩大于21。如果它们的数量有限,则其中一条将具有最高的秩-这意味着该秩仍具有上限。 当四位数学家看到这一点时,他们意识到自己手中有了活生生的成果。
伍德说:“这一预测与每个人的信念都不一致,至少他们公开承认了这一观点。” “没有人相信等级可能有局限性。”
如果对模型的信念需要一个相当严肃的步骤,那么当模型报告常识是错误的时,则需要更大的步骤。 但是,有很多证据支持这一结果。 该模型基于其他数学家创建的先前模型,这些数学家已经研究了椭圆曲线的各种特性。 这些模型经受了时间的考验。 这些预测中的一些甚至已经得到证明。
伍德说:“没有人建议从头开始并制造一种新模型。” “问题是如何丰富人们已经相信的现有模型。”
相信该模型的另一个原因是,等级值21似乎不是任意边界。 十年前,格兰维尔(Granville)创建了另一种模型,从中得出的结论是,只有数量有限的椭圆曲线的秩高于21。格兰维尔模型与当前模型完全不相似-并且两者都赋予了秩21显着的事实是从许多数学家的角度来看,这完全不同于简单的巧合。
帕克说:“我们有两种完全不同的启发式模型,并且都给出了相同的数字21,这使人们感到惊讶。”
该模型似乎可信的最令人信服的原因是,其其他预测几乎与椭圆曲线的已验证特性完全匹配。 该模型的一般结论(存在数量超过21的有限数量的椭圆曲线)适用于所有椭圆曲线。 但是,他们有一定的家族,其中许多数学家已经确定了等级界限。 该模型还预测了其中许多家族的等级值,并且其预测是相似的,甚至与数学家已经确定的边界完全一致。
帕克说:“我们的边界准确地预测了其他人研究过的所有这些病例。” “人们对我的报告表示怀疑,但是当我提到其他巧合时,他们对此感到非常惊讶。”
在证据与证据之间
该模型有很多支持,但并非所有人都相信它,并且可能证明是错误的。 最重要的怀疑者是哈佛数学家Noam Elkis,他创造了椭圆曲线的排名记录。 自从他成为哈佛最年轻的全职教授以来的几十年中,他收到了几项表明没有职等界限的结果。 “我的看法很长一段时间都没有改变-我认为我们不精通这个问题来支持这个或那个假设,”埃尔基斯通过邮件给我写信。
Elkis认为该模型可能在许多方面无法正常工作。 它考虑了随机选择的曲线,或者某种意义上的曲线是平均的。 但是,包括Elkis本人的研究在内的证据表明,存在椭圆曲线族的可能性,每个椭圆曲线族都包含无限数量的此类曲线,其行为与典型曲线的行为显着不同。 Elkis写道:“基于随机曲线预期行为的启发式模型可能无法说明极端行为的全部情况。”
即使是该模型的作者之一也不能完全确定它。 伍德说:“我会说我的身份有限,就像一个不可知论者。” 她承认该模型可能由于Elkis所说的原因而不正确。 但是,如果模型不能处理任务,则因为它没有考虑椭圆曲线的某些隐藏和意外属性。 “问题是:如果您不相信排名有限,该模型将在哪里停止运作?” 伍德说。
“最有可能的是,如果有人不提出自己错的巧妙理由,那么他们将是正确的。 我不知道是否存在这样的原因,”与Elkis合作并研究椭圆曲线等级的哈佛大学研究生Alexander Smith说。
该模型的作者并未将其重要性提升至教条。 他们知道证据与证据之间的区别,并且他们知道前者不会导致后者。 但是他们认为,至少经过一个世纪的简单推理,他们的工作至少为反思基本数学概念提供了合理的基础。
帕克说:“也许找到高阶椭圆曲线对数学家来说是一个挑战。” 或者,也许数学家“应该重新考虑他们对我们所相信的观点的看法,这是一种流行的假设”。