Geekly articles weekly

您的计算机内存滞后每7.8μs


现代DDR3 SDRAM。 资料来源： BY-SA / Kjerish 4.0

在最近访问山景城的计算机历史博物馆时 ，一个古老的铁氧体存储器实例引起了我的注意。


资料来源： BY-SA / Konstantin Lanzet 3.0

我很快得出结论，我不知道这些事情是如何工作的。 环是否旋转（否），以及为什么每根环都绕过三根导线（我仍然不知道它们的工作原理）。 更重要的是，我意识到我对现代动态RAM的工作原理一无所知！


资料来源： Ulrich Drapper的记忆周期

我对动态RAM如何工作的后果之一特别感兴趣。 事实证明，数据的每一位都是通过电荷（或不存在电荷）存储在RAM芯片中的微小电容器上的。 但是这些电容器会随着时间逐渐失去电荷。 为避免丢失存储的数据，必须定期更新它们以将费用（如果有）恢复到原始水平。 此更新过程涉及读取每个位，然后将其写回。 在此“更新”期间，内存繁忙，无法执行正常操作，例如写入或存储位。

这困扰了我很长时间，我想知道...是否可以注意到程序级别的更新延迟？

动态RAM升级培训基地


每个DIMM由“单元”和“行”，“列”，“侧面”和/或“列”组成。 犹他大学的这份演讲解释了术语。 可以使用decode-dimms检查计算机的内存配置。 这是一个例子：

  $解码尺寸
大小4096 MB
银行x行x列x位8 x 15 x 10 x 64
排名2

我们不需要了解整个DDR DIMM方案，我们希望了解仅一个存储一位信息的单元的操作。 更准确地说，我们只对更新过程感兴趣。

考虑两个来源：


动态内存中的每个位都必须更新：这通常每64毫秒发生一次（所谓的静态更新）。 这是相当昂贵的操作。 为了避免每64毫秒发生一次重大停机，该过程分为8192个较小的更新操作。 在它们的每一个中，计算机的内存控制器都将更新命令发送到DRAM芯片。 收到指令后，芯片将更新1/8192单元。 如果进行计数，则64 ms / 8192 = 7812.5 ns或7.81μs。 这意味着：

  • 每7812.5 ns执行一次更新命令。 它称为tREFI。
  • 更新和恢复过程需要一些时间，因此芯片可以再次执行正常的读写操作。 所谓的tRFC等于75 ns或120 ns（如上述Micron文档中所述）。

如果内存很热（超过85°C），则内存中的数据存储时间会减少，静态更新时间将减半至32 ms。 因此，tREFI降至3906.25 ns。

典型的内存芯片正忙于更新生命周期的很大一部分：从0.4％到5％。 此外，内存芯片是典型计算机功耗的重要部分，其中大部分功耗用于升级。

在更新期间，整个内存芯片均被阻塞。 也就是说，内存中的每个位每7812 ns锁定75 ns以上。 让我们测量一下。

实验准备


为了以纳秒的精度测量操作，您需要一个非常紧凑的周期，也许以C为单位。它看起来像这样：

  for (i = 0; i < ...; i++) { //   . *(volatile int *) one_global_var; //   CPU.    _mm_clflush(one_global_var); //   ,     //    (25    160). // , - . asm volatile("mfence"); //     clock_gettime(CLOCK_MONOTONIC, &ts); }

完整代码可在GitHub上获得。

代码很简单。 执行内存读取。 我们从CPU缓存中转储数据。 我们测量时间。

（注意：在第二个实验中，我尝试使用MOVNTDQA加载数据，但这需要特殊的不可缓存内存页和root权限）。

在我的计算机上，该程序显示以下数据：

  ＃时间戳记，循环时间
 3101895733，134
 3101895865，132
 3101896002，137
 3101896134、132
 3101896268、134
 3101896403，135
 3101896762，359
 3101896901，139
 3101897038，137

通常，会获得一个持续时间约为140 ns的周期，时间会周期性地跳至约360 ns。 有时，奇怪的结果会弹出3200 ns。

不幸的是，数据太嘈杂。 很难确定更新周期是否存在明显的延迟。

快速傅立叶变换


在某个时候，它突然降临在我身上。 由于我们要查找固定间隔的事件，因此我们可以将数据提交给FFT算法（快速傅里叶变换），该算法对主要频率进行解密。

我并不是第一个考虑这一点的人：马克· 西伯恩（ Mark Seaborn）着名的罗汉默（Rowhammer）漏洞是在2015年实施的。 即使查看了Mark的代码，要使FFT正常工作也比我预期的要难。 但最后，我将所有内容放在一起。

首先，您需要准备数据。 FFT要求输入具有恒定采样间隔。 我们还希望修整数据以减少噪声。 通过反复试验，我发现在对数据进行初步处理后可获得最佳结果：

  • 循环迭代的较小值（小于平均1.8）会被截断，忽略并替换为零。 我们真的不想制造噪音。
  • 所有其他读数都将替换为单位，因为由某些噪声引起的延迟幅度对我们而言实际上并不重要。
  • 我将采样间隔定为100 ns，但是任何奈奎斯特频率（两倍于预期频率）的数字都可以 。
  • 数据必须在固定时间采样，然后再提交给FFT。 所有合理的采样方法都可以正常工作，我决定采用基本线性插值法。

该算法是这样的：

 UNIT=100ns A = [(timestamp, loop_duration),...] p = 1 for curr_ts in frange(fist_ts, last_ts, UNIT): while not(A[p-1].timestamp <= curr_ts < A[p].timestamp): p += 1 v1 = 1 if avg*1.8 <= A[p-1].duration <= avg*4 else 0 v2 = 1 if avg*1.8 <= A[p].duration <= avg*4 else 0 v = estimate_linear(v1, v2, A[p-1].timestamp, curr_ts, A[p].timestamp) B.append( v )

在我的数据上哪个会产生像这样的相当无聊的向量：

  [0，0，0，0，0，0，1，0，0，0，0，0，0，0，0，0，0，0，0， 
  0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，1，1，0，
  0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0， 
  0，0，1，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，0，...]

但是，向量很大，通常约为20万个数据点。 有了这些数据，就可以使用FFT！

 C = numpy.fft.fft(B) C = numpy.abs(C) F = numpy.fft.fftfreq(len(B)) * (1000000000/UNIT)

很简单，对吧？ 这产生两个向量：

  • C包含复数的频率分量。 我们对复数不感兴趣，您可以使用abs()命令使它们变平滑。
  • F包含标签，该标签的频率跨度位于向量C的哪个位置。我们通过乘以输入向量的采样频率将指数归一化为赫兹。

结果可以绘制在图表上：



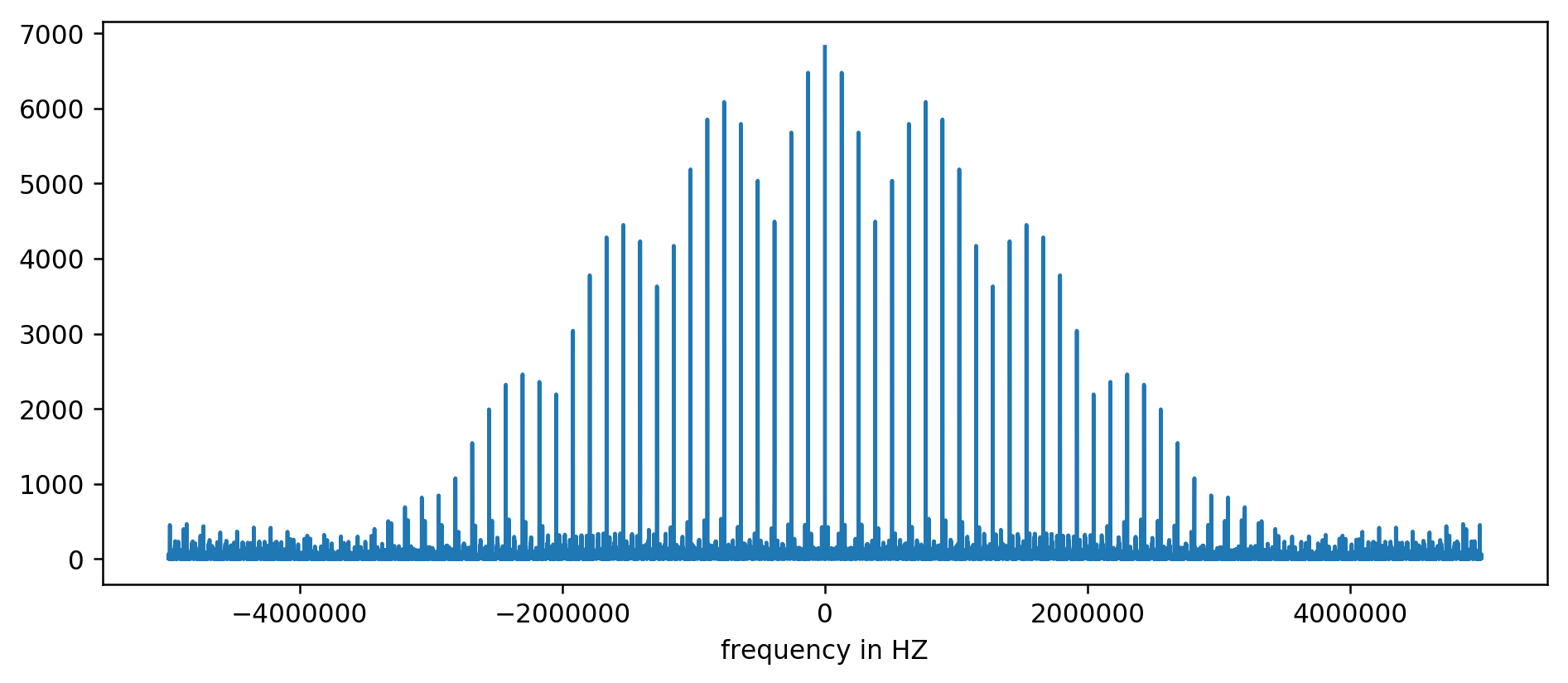
Y轴无单位，因为我们将延迟时间归一化。 尽管如此，在某些固定频率范围内仍清晰可见突发。 让我们更仔细地考虑它们：



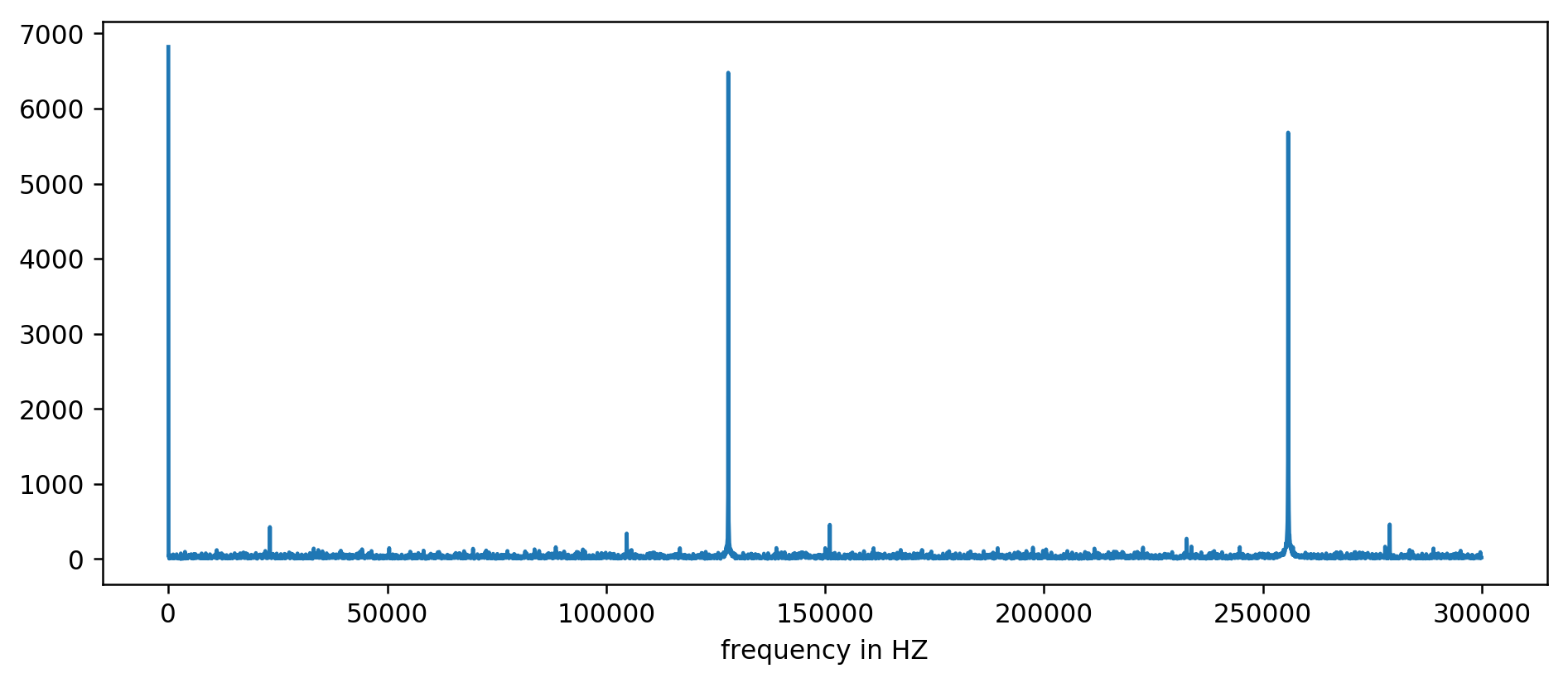
我们清楚地看到了前三个高峰。 经过一番表达，包括过滤读数至少是平均值的十倍之后，您可以提取基本频率：

  127850.0
 127900.0
 127950.0
 255700.0
 255750.0
 255800.0
 255850.0
 255900.0
 255950.0
 383600.0
 383650.0

我们认为：1000000000（ns / s）/ 127900（Hz）= 7818.6 ns

万岁！ 频率的第一跳确实是我们想要的，并且确实与更新时间相关。

256 kHz，384 kHz，512 kHz的其余峰值就是所谓的谐波，是我们128 kHz基本频率的倍数。 这是将FFT应用于方波之类的完全预期的副作用。

为了方便实验，我们为命令行创建了一个版本 。 您可以自己运行代码。 这是在我的服务器上启动的示例：

  〜/ 2018-11-内存刷新$ make
 gcc -msse4.1 -ggdb -O3 -Wall -Wextra measure-dram.c -o measure-dram
 ./measure-dram |  python3 ./analyze-dram.py
 [*]验证ASLR：main = 0x555555554890堆栈= 0x7fffffefe2ec
 []有趣的事实。 我每秒做了40663553 clock_gettime（）
 [*]测量MOVQ + CLFLUSH时间。 运行131072次迭代。
 [*]写出数据
 [*]输入数据：最小值= 117平均= 176中值= 167最大值= 8172项= 131072
 [*]截止范围212-inf
 []截止值以下127849项，截止值以上0项，非零3223项
 [*]运行FFT
 [*] 250kHz以下2kHz以上的最高频率为7716
 [+]高于2kHZ的最高频率尖峰在：
 127906Hz 7716
 255813Hz 7947
 383720Hz 7460
 511626Hz 7141

我必须承认，代码并不完全稳定。 如果出现问题，建议禁用Turbo Boost，CPU频率缩放和性能优化。

结论


这项工作有两个主要结论。

我们看到低级数据很难分析，而且看起来很嘈杂。 不用肉眼评估，您总可以使用良好的旧FFT。 从某种意义上说，在准备数据时，一厢情愿是必要的。

最重要的是，我们已经表明，通常可以通过用户空间中的简单过程来测量微妙的硬件行为。 这种想法导致发现了原始的Rowhammer漏洞 ，该漏洞已在Meltdown / Spectre攻击中实现，并在最近的Rowhammer ECC内存转世中再次得到证明。

许多内容仍然超出了本文的范围。 我们几乎没有涉及内存子系统的内部操作。 为了进一步阅读，我建议：


最后，这是旧铁氧体存储器的良好描述：

Source: https://habr.com/ru/post/zh-CN431010/

More articles:


All Articles