亚历山大·史密斯（Alexander Smith）在Goldfeld假设上的工作揭示了椭圆曲线的基本特性
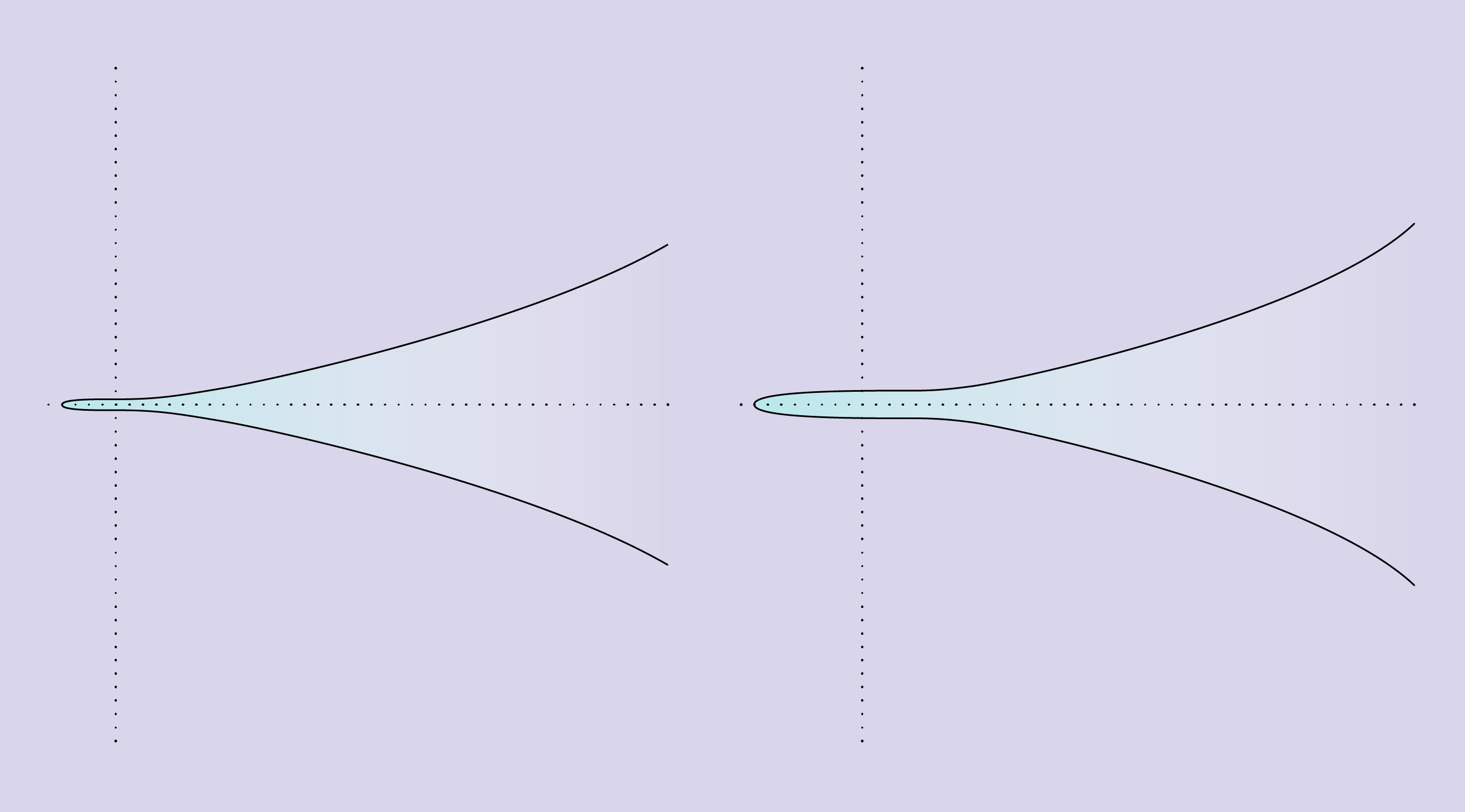两条椭圆曲线说明了等级概念的奇怪之处。 左边的曲线由等式y 2 = x 3 + 1来描述，仅通过五个有理点并具有等级0。右边的曲线由等式y 2 = x 3 + 8来描述，其经过无限个有理点，并且具有等级1。椭圆曲线可以有很多变体，但是它们的真实变体只有两个。 这是哈佛大学研究生获得的新证据的结果。
椭圆曲线看似奇特，但它们是不起眼的几何对象，没有比直线，抛物线或椭圆更复杂的了。 在去年在线发表的
著作中 ，
Alexadr Smith证明了40年前有关秩椭圆曲线基本特征的假设。 Smith证明，对于具有一个特征的给定曲线族，一半的等级为0，一半的等级为1。
这一结果确立了已经占据了许多世纪的数学家的对象的支持特性，在最近几十年中，其重要性尤其得到提高。
“我们已经考虑了1000多年，现在我们对椭圆曲线有了概率的了解。 普林斯顿大学的数学家
张绍乌说，这非常重要。
椭圆曲线是将变量提高到三次方的方程，例如y
2 = x
3 +1。在最近几十年中，
椭圆曲线出现在许多重要的数学证明中，包括1994年
以来费马大定理的最重要证明。 它们的部分意义在于它们属于最复杂类型的多项式方程，数学家对此具有某种系统性的想法。
哥伦比亚大学的数学家
Dorian Goldfeld说：“椭圆曲线是一个有趣的例子。”他在1979年提出了一个以他的名字命名的假设。
Goldfeld假设对椭圆曲线的等级进行了预测。 正如我们在最近的一篇文章中已经描述的那样：“
如果没有严格的证明 ，
那么哪些证据可以说服数学家？ ”等级是对曲线的一组理性解（可以表示为分数的解）的复杂性的度量。 尽管曲线上的秩没有经过证明的限制（到目前为止，最高的28个被认为是最高的），但Goldfeld假设预测，椭圆曲线的平均一半的等级为0，另一半的等级为1。
如果椭圆形曲线的一半的秩为0，另一半的椭圆形为1，那么对于您来说，可能似乎还不存在秩大于1的椭圆曲线。如果您有一盒乒乓球，并且知道一半它们是黑色的，一半是白色的，那么不能有红色的。
更令人困惑的是，等级为2或更高的椭圆曲线不仅存在数不胜数，而且存在无限数量。 看似荒谬的结果是狡猾的统计数据与无限性共同作用的结果。 即使有很多2级及以上的曲线，也有0级和1级的曲线如此之多，以至于2级及以上的曲线在统计上并不显着。 如果将所有曲线放在一个盒子中并从那里随机取出，那么拉出等级大于1的曲线的机会正式等于零。
曲线的等级为0是什么意思？ 这样的曲线有一定数量的有理点-最多不超过16个，如
Barry Mazur在1970年代所证明的。
多里安·戈德菲尔德有理由相信，大量的椭圆曲线的等级为0。如果您想象一条曲线如何沿平面运行，就会发现它经过的大多数点都不合理。 即使这些点任意复杂，也不能将它们表示为分数。 随机曲线与许多有理点（无限集）相交的机会很小。
史密斯说：“我是这样认为的：如果你选择一条随机的椭圆曲线，那么它将有理由获得等级0。它并不想有理性的点。”
以类似的方式解释了等级1曲线的普遍性。 等级1的曲线具有无限多个有理点，但是它们都非常整齐地对齐，因此您可以在一个相当简单的过程中将它们彼此连接。
对于等级2和更高的曲线，有理点的集合更加复杂。 它们包含彼此不相关的几个有理点的无限子集。
“出现两个独立点的机会是什么？ -戈德菲尔德说。 “很低。” 我的假设说，这种情况很少发生。”
当Goldfeld首次提出他的假设时，大多数数学家都认为它是错误的。 他们指出了计算实验的结果，据此，等级为2或更高的曲线的发生频率要比0％的情况高得多。
Goldfeld回答说，他们只是把范围太小了。 他指出，如果仅研究前10个整数，则可能会得出极其不准确的估计，即40％的数字是质数。 类似地，这些计算实验已从椭圆曲线的小子集外推到无限大的曲线族。
“我说看素数！ 那是我的答案。 我们需要爬得更高，因为一开始会出现很多乐趣，”戈尔德菲尔德说。
Goldfeld假设并不适用于所有椭圆曲线。 它描述了特殊的椭圆曲线，二次扭曲系列。 示例：椭圆曲线cy
2 = x
3 -x，其中c是常数。 通过更改c的值，可以弯曲椭圆曲线。 戈德费尔德假设是指可以通过更改c的值来获得的曲线的无限多种。
亚历山大·史密斯（Alexander Smith）作证说，戈德菲尔德是正确的。 在一篇新论文中，他证明了（特殊类型的）椭圆曲线的100％的等级为0或1。他还证明了这些曲线在两个等级之间均分，尽管有一个陷阱。 他对50–50划分的证明是基于
Birch – Swinnerton-Dyer （BJD）
假设的有效性。 BSD假设是数学中最著名的开放问题之一。 数学家尚未接近证明，但总的来说，他们认为它是正确的。
即使有这样的警告，史密斯的结果仍然被认为是重要的。 数学家说，他展示了一种方法，可以充分证明Goldfeld假设，而无需修改令人沮丧的BSD假设。 这种方法使人们对椭圆曲线的性质有了新的认识。
威斯康星大学的数学家
梅兰妮·伍德说：“亚历克斯·史密斯的工作非常有趣，我认为还有待研究，并应得到应有的成果。” “可以证明这一事实非常重要且具有革命性。”