使用Verilog HDL的开关发生器的实际实现

摘要

线性反馈移位寄存器是在硬件中实现伪随机位发生器的绝佳工具。 它们抑制了简单有效的电子结构。 此外，它们能够产生具有大周期和良好统计特性的输出序列。 但是，由于使用Berlekamp-Massey算法在给定少量密钥流位的情况下可以唯一地预测输出序列，因此标准LFSR并不是加密安全的。 已经提出了几种破坏LFSR设计固有的线性的方法。 这些方法包括非线性组合发生器，非线性滤波器发生器和时钟控制发生器。 然而，它们仍然容易受到许多攻击，例如边通道攻击和代数攻击。 2015年，提出了一种新的时钟受控发电机，称为开关发电机。 事实证明，这种新型发生器能够抵抗代数攻击和边信道攻击，同时又能保持效率和安全性要求。 在本项目中，我们介绍了使用Verilog HDL的开关发生器的设计。

引言和历史背景

硬件中伪随机数生成的历史与流密码的发展紧密相关。 与将大块（64位或更多）纯文本加密的块密码不同，流密码是分别对纯文本字符（通常一点一点）加密的密码。 许多流密码体系结构需要密钥流生成器，该密钥流生成器是伪随机位生成器，其种子是加密密钥。 对于每个纯文本位，将相应的密文位计算为纯文本位和相应的密钥流位的某些可逆函数（通常是异或门）。 因此，设计安全有效的密钥流生成器对于流密码操作至关重要。


用于构建密钥流生成器的一种有用工具是线性反馈移位寄存器。 可以使用基本电子组件轻松构建它们，并且可以在可编程逻辑设备上简单地对其进行编程。 而且，由于它们的结构简单，可以对LFSR进行数学建模和分析，这导致了有关它们的大量知识和结果。 正确构造的LFSR的输出序列具有指数长度和良好的统计特性，例如较大的线性复杂度。


尽管LFSR具有良好的统计特性，但由于其线性特性，不能用作标准形式的密钥流生成器。 如果攻击者设法知道 $$$2L$连续的密钥流位，然后可以使用Berlekamp-Massey算法唯一有效地预测输出序列，其中 $$$L$是寄存器的数量。 提出了许多不同的方法来破坏LFSR输出序列中固有的线性度：

• 使用多个LFSR及其输出的非线性组合功能（非线性组合生成器）。
• 将输出序列生成为LFSR状态的某些非线性函数（非线性滤波器生成器）。
• LFSR（时钟控制的发生器）的时钟不规则。

尽管如此，所有这些设计仍然容易受到诸如代数和旁通道攻击之类的攻击。 2000年之后，这不再是一个关键的问题，因为提出了分组密码Rijndael并被选为高级加密标准（AES）。 AES能够以流密码模式运行，并满足流密码的所有工业标准。 此外，随着计算能力的提高，AES可以部署在各种平台上。 这已导致流密码应用程序的显着减少。


阿迪·沙米尔（Adi Shamir）在“ Stream Ciphers 2004”和“ Asiacrypt 2004”中介绍了最新技术，主题为“ Stream Ciphers：死还是生？”。 在他的演讲中，他建议流密码可以在以下应用程序中生存：

• 速度非常快的面向软件的应用程序（例如路由器）。
• 占用空间极小的面向硬件的应用程序（例如智能卡）。

密钥流生成器的最新建议之一是开关生成器。 据称，它在保持效率和运行速度的同时，还能抵抗代数和旁道攻击。


在这个项目中，我们将使用Verilog HDL在硬件上介绍开关发生器的设计。 首先，我们介绍两种常见的LFSR形式：斐波那契LFSR和Galois LFSR。 接下来，我们提出LFSR的数学表示。 然后，我们将介绍引入的开关发生器。 最后，我们介绍了开关发生器的Verilog设计。

线性反馈移位寄存器

线性反馈移位寄存器是由线性列表的寄存器（也称为延迟元件）及其之间的预定义连接组成的电路。 全局（单个）时钟信号控制LFSR内部的数据流。 两种最常用的LFSR类型是斐波那契LFSR和Galois LFSR。 仅以连接形式延迟。 正如我们将在稍后的数学模型部分中看到的那样，斐波那契和Galois体系结构之间有许多相似之处，其中一种优于另一种是特定于应用程序的。


在本文中，我们假设一个假设的全局时间计数器始于 $$$0$并增加 $$$1$在全局时钟周期的每个上升沿之后。

寄存器

寄存器是一种逻辑元件，能够存储称为状态的一位数据。 它有两条输入线：一位数据线和一条时钟信号线。 它具有始终等于内部状态的一位输出。 在时钟输入的每个上升沿，将数据输入分配给状态，否则状态保持不变。 让我们表示寄存器的状态 $$$S$在时间 $$$t$作为 $$$\ mathop S \ nolimits ^ t$。

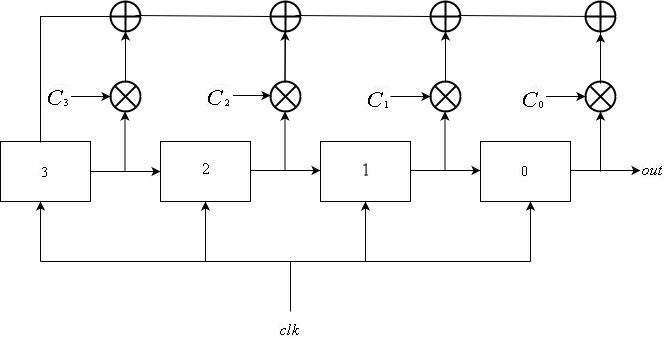
斐波那契

斐波那契LFSR包含 $$$L$从中枚举的寄存器 $$$0$到 $$$L-1$，都连接到相同的时钟信号。 输入寄存器 $$$我$是寄存器的输出 $$$我+ 1$为 $$$0 \ le我\ le L-2$。 寄存器的反馈输入 $$$L-1$是某些寄存器子集的输出的异或。 寄存器更新可以用以下数学方式描述：

$$

$$\ mathop S \ nolimits_i ^ t = \ left \ {\开始{array} {l} \ mathop S \ nolimits_ {i + 1} ^ {t-1} {\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ rm {if} \ \} 0 \ le i \ le L-2 \\ \ mathop \ bigoplus \ limits_ {j = 1} ^ k \ mathop S \ nolimits_j ^ {t-1} \ otimes \ mathop C \ nolimits_j {\ \ \ \ \ rm {if} \ \} i = L-1 \ end {array} \ right。$$

在哪里 $$$C_j = 1$如果注册 $$$j$包含在反馈中， $$$0$否则。

输出序列从寄存器获得 $$$0$。 也就是说，输出顺序为 $$$\ mathop {\左\ {{\ mathop S \ nolimits_0 ^ i} \ right \}} \ nolimits_ {i \ ge 0}$ 。

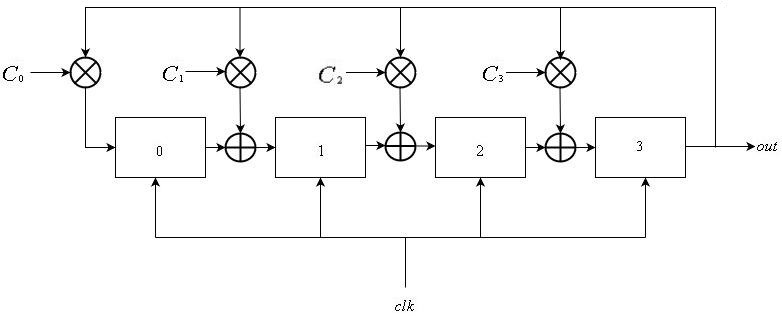
Galois LFSR

Galois LFSR还包含一个线性列表 $$$L$从中枚举的寄存器 $$$0$到 $$$L-1$，所有共享全局时钟信号。 输入寄存器 $$$我$是寄存器的输出 $$$i-1$为 $$$1 \ le我\ le L-1$。 对于寄存器的某些子集，其输入与寄存器的输出异或 $$$L-1$。 可以表示为：

$$

$$\ mathop S \ nolimits_i ^ t = \左\ {\开始{array} {l} \ mathop S \ nolimits_ {i-1} ^ {t-1} \ oplus \ mathop S \ nolimits_ {L-1} ^ {t-1} \ otimes \ mathop C \ nolimits_i {\ rm {\ \ \ \ if \ \}} 1 \ le i \ le L-1 \\ \ mathop S \ nolimits_ {L-1} ^ {t- 1} \ otimes \ mathop C \ nolimits_0 {\ rm {\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ if \ \}} i = 0 \ end {array} \ right。$$

在哪里 $$$C_i = 1$如果输入寄存器 $$$我$与寄存器的输出异或 $$$L-1$。


以类似于斐波纳契LFSR的方式，将输出序列定义为 $$$\ mathop {\左\ {{\ mathop S \ nolimits_ {L-1} ^ i} \ right \}} \ nolimits_ {i \ ge 0}$ 。

斐波那契和伽罗瓦设计之间的比较

在数学意义上，斐波那契和伽罗瓦LFSR之间存在直接对应关系，我们将在下一部分中看到。 但是，使用Galois的设计有两个明显的优点：

• 在软件实施中，它不需要 $$$L$位奇偶校验，这增加了复杂度的对数因子。
• 在硬件实现中，它仅需要两个输入异或门，其传播延迟显着小于斐波那契设计中使用的多输入异或门。

在我们的项目中，我们考虑了LFSR的矩阵公式，因此两种架构都是可以互换的。

LFSR的数学模型

在以下各节中，除非另有说明，否则我们假定所有计算均在Galois字段下完成 $$$Gf \左（2 \右）$。 也就是说，所有运算都是以模运算 $$$2$。 此约定的另一种实现是，所有乘法都是逻辑与门，所有求和都是异或门。


考虑所有状态 $$$L$LFSR在某些时候的寄存器 $$$t$; 这可以表示为来自 $$${\左\ {{0,1} \右\} ^ L}$ ：

$$

$${S ^ t} = \左（{\ mathop S \ nolimits_0 ^ t; \ mathop S \ nolimits_1 ^ t; \ ldots; \ mathop S \ nolimits_ {L-1} ^ t} \ right）$$

我们将此向量表示为LFSR的状态。 请注意，最多 $$${2 ^ L}$可能的状态 $$$L$注册LFSR。 还要注意，如果LFSR要达到全零状态，则它不能达到任何其他状态。 因此我们说有 $$$2 ^ L-1$LFSR的重要性。


考虑以下线性变换：

$$

$$F = \左（{\ begin {array} {* {20} {c}} 0＆1＆\ cdots＆0 \\ \ vdots＆\ vdots＆\ ddots＆\ vdots \\ 0＆0＆\ cdots＆1 \\ {\ mathop C \ \ nolimits_0}＆{\ mathop C \ nolimits_1}＆\ cdots＆{\ mathop C \ nolimits_ {L-1}} \ end {array}} \ right）$$

鉴于 $$$\ mathop S \ nolimits ^ t$是斐波纳契LFSR的状态，可以观察到

$$

$$F \ cdot \ mathop S \ nolimits ^ t = \ mathop S \ nolimits ^ {t + 1}$$

如果 $$$\ mathop S \ nolimits ^ t$处于伽罗瓦（Galois）LFSR的状态，然后考虑转变 $$$G$：

$$

$$G = \ left（{\ begin {array} {* {20} {c}} 0＆\ cdots＆0＆{\ mathop C \ nolimits_0} \\ 1＆\ cdots＆0＆{\ mathop C \ nolimits_1} \\ \ vdots＆ \ ddots＆\ vdots＆\ vdots \\ 0＆\ cdots＆1＆{\ mathop C \ nolimits_ {L-1}} \ end {array}} \ right）$$

在这种情况下，我们有

$$

$$G \ cdot \ mathop S \ nolimits ^ t = \ mathop S \ nolimits ^ {t + 1}$$

在处理重复更新时，LFSR的矩阵表示形式可以很灵活，因为它们可以解释为简单的矩阵乘积。 可以观察到 $$$F = {G ^ T}$。 这个事实表明，如果将斐波那契和伽罗瓦设计视为来自 $$${\左\ {{0,1} \右\} ^ N}$ 到 $$${\左\ {{0,1} \右\} ^ N}$ 。


将某个LFSR的状态向量乘以矩阵（Fiboancci或Galois类型）被称为计时或更新LFSR。

开关发电机

开关发生器是2015年提出的时钟控制发生器。事实证明，它具有抵抗代数和旁通道攻击的能力。 在本节中，我们将介绍其发明者所指定的开关发生器的设计。

基本结构

开关发生器由两个LFSR组成：控制LFSR $$长度 $$$N$和数据LFSR $$$B$长度 $$$M$。 控制LFSR如前所述进行更新。 但是，数据LFSR使用两种可能的矩阵之一进行更新， $$$\ mathop M \ nolimits_1 ^ i$或 $$$\ mathop M \ nolimits_2 ^ j$，在哪里 $$${M_1}，{M_2}$是一些原始多项式的伴随矩阵。 从控制LFSR输出的信号确定在另一个矩阵上选择一个矩阵。 此过程可以描述如下：

$$

$$\ mathop B \ nolimits ^ t = \左\ {\开始{array} {l} \ mathop M \ nolimits_1 ^ i \ cdot \ mathop B \ nolimits ^ {t-1} {\ rm {\ \ \ \ if \ \}} \ mathop A \ nolimits_ {M-1} ^ t = 0 \\ \ mathop M \ nolimits_2 ^ j \ cdot \ mathop B \ nolimits ^ {t-1} {\ rm {\ \ \ \如果\ \}} \ mathop A \ nolimits_ {M-1} ^ t = 1 \ end {array} \对$$

开关发生器的输出是LFSR的输出 $$$B$。 请注意，我们假设 $$是Galois LFSR。 它也可以是斐波那契LFSR。


整数 $$$我，j$被称为切换索引。

种子

回想一下，LFSR最多可以迭代一次 $$${2 ^ L} -1$非平凡的州，然后再访问以前的州。 自矩阵 $$${M_1}，{M_2}$是LFSR的变换矩阵，我们可以推导出整数 $$$我，j$最多可以 $$$2 ^ M-1$在矩阵开始重复之前。


开关发生器的种子是 $$$N + 3M$位，代表LFSR的初始状态 $$和 $$$B$和整数幂 $$$我，j$。 注意矩阵 $$${M_1}，{M_2}$在整个实施过程中是固定的，不包含在种子中。

Verilog设计

在本节中，我们将介绍使用Verilog HDL的开关发生器的设计。 我们将以自下而上的方式介绍每个模块的设计。 最后，我们介绍了开关发生器模块。


在我们的设计中，我们试图将同步组件保持在最低限度。 仅有的时钟控制组件是LFSR $$$A，B$。


矩阵和向量运算可以通过多种不同的方法来实现，这些方法在逻辑单元的消耗，存储单元和过程复杂性方面都不同。 在我们的设计中，我们消除了对过程块的需求，并最大限度地使用了逻辑元素。


以下模块中的所有矩阵均从以下位置开始编制索引 $$$0$从左到右，然后从上到下。


还要注意，所有模块都有参数化的大小。 这是出于调试目的。 在实际的实现中，所有大小都是固定的。

多路复用器

这是一个实现2对1的模块 $$$N$位多路复用器。 该模块有两个 $$$N$位输入线，1位选择器线和 $$$N$位输出线。 如果选择器输入为 $$$0$然后将输出设置为第一条输入线，否则将其设置为第二条输入线。


多路复用器模块

向量转换

该模块对向量执行线性变换。 它接受输入 $$$N \倍N$变换矩阵和 $$$N$位向量。 它输出其输入的矩阵向量乘积。


输出向量中的每一位都是 $$$N$位异或门，以输入的结果为输入 $$$N$输入向量和相应矩阵行的按位和。 也就是说，每个输出位都硬连接到输入，不需要任何程序块。


恰好 $$$N ^ 2$使用两个输入和门，以及 $$$N$$$$N$-输入异或门。


向量转换模块

身分识别

该模块不接受任何输入。 其 $$$N \倍N$位输出初始化为 $$$N$单位矩阵 为了方便起见，声明了这样的模块，因此我们不必为每个不同的大小初始化全局寄存器向量。


身份矩阵模块

转置

该模块接受 $$$N \倍N$矩阵并输出其转置。 此模块中既不使用逻辑也不使用存储器元素，其输出仅是其输入的排列
。

矩阵转置模块

矩阵乘法

这是一个实现矩阵矩阵乘法的模块。 它接受两个 $$$N \倍N$矩阵作为输入，并输出其矩阵矩阵乘积。


该模块包含矩阵转置模块的一个实例。 这使得可以将连续索引分配给第二输入矩阵中的列。 然后，将输出矩阵中的每个条目分配给 $$$N$-输入异或门，其输入是按位和从第一个矩阵起的对应行，从第二个矩阵起的列。


恰好 $$$N ^ 3$二输入和门 $$$N ^ 2$$$$N$-input xor用于此实现。


矩阵乘法模块

矩阵求幂

该模块将矩阵提高到整数幂。 它接受输入 $$$N \倍N$矩阵和 $$$K$位整数。 它的输出是升到指定整数幂的矩阵。


矩阵幂运算模块

控制单元

该模块实现了 $$$N$位控制LFSR。 它是我们设计中两个时钟控制模块之一。


它包括一个静态 $$$N \倍N$LFSR转换矩阵和变量 $$$N$位状态。 它的输入包括一个时钟，一个 $$$N$位状态复位和复位信号。 它的输出是一位，它是LFSR的最后一位。


在时钟信号的每个上升沿之后，使用矩阵矢量乘法模块根据变换矩阵更新状态。 在复位信号的每个上升沿之后，将状态复位分配给内部状态。





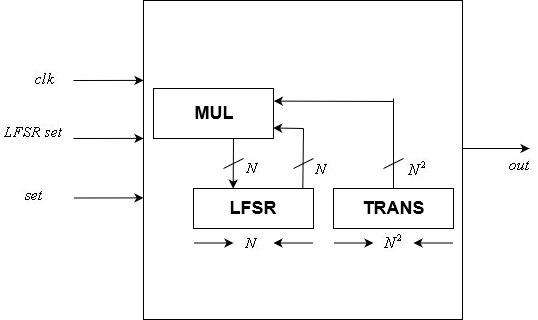控制单元模块

数据单位

的 $$$N$数据LFSR使用此模块实现。 像控制单元模块一​​样，它是时钟控制的


该模块包括两个 $$$N \倍N$变换矩阵和 $$$N$位LFSR状态。 它接受时钟信号，控制信号， $$$N$位LFSR状态复位，两个 $$$N \倍N$矩阵变换复位，并产生复位信号。 它具有一位输出，即内部LFSR的最后一位。


注意，由于可以改变种子，所以也可以改变变换矩阵，这与控制单元的变换矩阵是否固定不同。




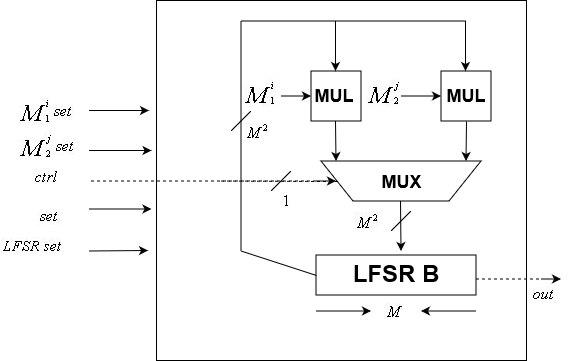\数据单位

开关发电机

这是我们设计的主要模块。 它由整数参数化 $$$N，M$，分别是控件和数据单元的大小。


该模块的输入是时钟信号， $$$N + 3M$位种子和置位信号。 种子只是控制LFSR重置，数据LFSR重置和整数的串联 $$$我，j$它的输出是一位，是开关发生器产生的伪随机位。


该模块包括两个 $$$M \乘以M$矩阵 $$$\ mathop M \ nolimits_1，\ mathop M \ nolimits_2$。 这些矩阵在整个实现过程中都是固定的。


两个矩阵求幂模块实例用于计算数据单元的输入矩阵，其中它们的输入是固定的变换矩阵和整数 $$$我，j$，从种子中提取。


开关发电机模块

结论与建议

在这个项目中，我们介绍了使用Verilog HDL的开关发生器的设计。 这种设计完全集中在硬件上，并且消除了对过程块的使用。 这种方法允许以逻辑和存储元件为代价的最大性能。 对于某些具有逻辑和存储元素约束的应用，牺牲性能并增加程序块的使用以减少电子元素的使用可能是有益的。


该项目的一个缺点是，它承担了为用户选择良好的开关指标的责任。 一种可能的进步是添加了一个硬件组件来检查所使用的交换索引的有效性。 这需要复杂算法的硬件实现，例如找到给定矩阵的特征多项式并检查其素数性。


可能的改进是添加一个真正的随机数生成器以检查随机切换索引，并在找到有效对后输出它们。 可以证明，此过程很可能在短时间内停止。

参考文献

1. Katz，Jonathan等。 应用密码学手册。 CRC出版社，1996年。
2. 崔俊等。 “开关发生器：新型时钟控制发生器，可抵抗代数和旁通道攻击。” 熵17.6（2015）：3692-3709。
3. 阿迪·沙米尔（Shamir，Adi）。 “流密码：死还是生？”。 ASIACRYPT。 2004。
4. 初学者的LFSR