学习潜伏期：排队论

随着时间的推移，延迟的主题不仅在Yandex中的不同系统中变得有趣。 当任何服务担保出现在这些系统中时，就会发生这种情况。 显然，事实是，重要的是不仅要向用户保证一定的机会，而且要保证在合理的响应时间内收到它。 对于不同的系统，响应时间的“合理性”当然会有很大的不同，但是在所有系统中表现出延迟的基本原理是很普遍的，可以将它们与具体情况分开考虑。

我叫Sergey Trifonov，我在Yandex中的Real-Time Map Reduce团队工作。 我们正在开发一个实时数据流处理平台，具有秒和亚秒级的响应时间。 该平台可供内部用户使用，并允许他们在不断传入的数据流上执行应用程序代码。 在过去的一百多年中，我将尝试简要介绍人类有关延迟分析的基本概念，现在，我们将尝试了解使用排队论可以确切地了解延迟。

据我所知，与排队系统（电话通信网络）的出现有关，已经开始系统地研究等待时间现象。 排队理论始于1909年A.K. Erlang的工作，其中他证明了泊松分布适用于随机电话业务。 Erlang开发了一种已经用于设计电话网络数十年的理论。 该理论使我们能够确定拒绝服务的可能性。 对于具有电路交换通道的电话网络，如果所有通道都忙并且无法进行呼叫，则会发生故障。 此事件的可能性必须加以控制。 我想保证，例如，将处理所有呼叫的95％。 如果知道呼叫的持续时间和数量，则使用Erlang的公式可以确定需要多少台服务器才能实现此保证。 实际上，这项任务只是关于质量保证，如今人们仍在解决类似的问题。 但是系统已经变得更加复杂。 排队理论的主要问题是，在大多数机构中，它都不被教，很少有人理解通常的M / M / 1队列之外的问题（请参阅下面的表示法），但是众所周知，生活比这个系统复杂得多。 因此，我建议绕过M / M / 1，立即转到最有趣的地方。

平均值

如果您不试图获得有关系统中概率分布的完整知识，而是专注于更简单的问题，则可以获得有趣且有用的结果。 当然，其中最著名的是利特尔定理 。 它适用于具有任何输入流，任何复杂性的内部设备以及内部具有任意调度程序的系统。 唯一的要求是系统必须稳定：平均响应时间和队列长度必须存在，然后通过简单表达式将它们连接起来

$$

$$L = \ lambda W$$

在哪里 $$$L$ -系统所考虑部分中请求的平均时间[pcs]， $$$W$ -请求通过系统此部分的平均时间， $$$\ lambda$ -接收系统请求的速度[pcs / s]。 该定理的优势在于它可以应用于系统的任何部分：队列，执行程序，队列+执行程序或整个网络。 通常，该定理的用法大致如下：“ 1Gbit / s的数据流涌向我们，我们测量了平均响应时间，它是10毫秒，因此，我们平均有1.25 MB的传输空间。” 因此，这种计算是不正确的。 更准确地说，只有所有请求的字节大小都相同时，才成立。 利特尔定理将查询按片段而不是字节进行计数。

如何使用利特尔定理

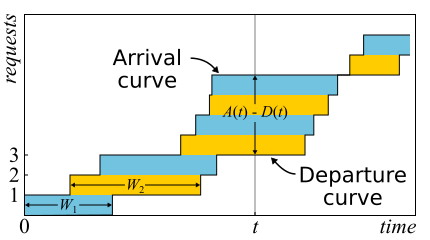
在数学中，通常需要研究证据以获得真正的见解。 就是这种情况。 利特尔定理是如此之好，我在这里给出了证明的草图。 传入流量由功能描述 $$$A（吨）$ -当时登录的请求数 $$$t$ 。 相似地 $$$D（吨）$ -当时已注销的请求数 $$$t$ 。 请求的进入（退出）时刻被视为其最后一个字节的接收（传输）时刻。 系统的边界仅由这些时刻决定；因此，该定理可广泛应用。 如果在同一轴上绘制这些函数的图形，则很容易看到 $$$A（t）-D（t）$ 是系统在时间t的请求数，并且 $$$W_n$ -第n个请求的响应时间。

该定理仅在1961年得到正式证明 ，尽管该关系本身在此之前就已为人所知。

实际上，如果可以在系统中对请求进行重新排序，那么一切都会有些复杂，因此为简单起见，我们将假定这种情况不会发生。 尽管该定理在这种情况下也是正确的。 现在让我们计算图表之间的面积。 有两种方法可以做到这一点。 首先，根据列-作为积分通常认为。 在这种情况下，事实证明，整数就是队列的大小。 其次，逐行-简单地增加所有请求的延迟。 显然，两个计算得出的面积相同，因此它们是相等的。 如果相等的两个部分都除以我们计算面积的时间Δt，那么在左侧，我们将获得平均队列长度 $$$L$ （根据平均值的定义）。 右边有些棘手。 我们需要向分子和分母添加另一个请求数N，然后我们将成功

$$

$$\ frac {\ sum W_i} {\ Delta t} = \ frac {\ sum W_i} {N} \ frac {N} {\ Delta t} = W \ lambda$$

如果我们考虑足够大的Δt或一个雇用期，则可以消除边缘的问题，并可以证明定理成立。

重要的是要说证明中我们没有使用任何概率的分布。 实际上，利特尔定理是确定性定律！ 这样的定律在操作法排队理论中被称为。 它们可以应用于系统的任何部分以及各种随机变量的任何分布。 这些定律构成了一个构造函数，可以成功地用于分析网络中的平均值。 缺点是它们都仅适用于平均值，并且不提供有关分布的任何知识。

回到为什么Little定理不能应用于字节的问题，假设 $$$A（吨）$ 和 $$$D（吨）$ 现在，它们的度量单位不是字节，而是字节。 然后，进行类似的论证，我们得到 $$$W$ 奇怪的是面积除以字节总数。 仍然是几秒钟，但这只是加权平均延迟，较大的请求获得更大的加权。 这个值可以称为字节的平均延迟-通常，这是合乎逻辑的，因为我们用字节替换了片段-但不是请求的延迟。

利特尔定理说，对于特定的请求流，响应时间与系统中的请求数量成比例。 如果所有请求看起来都一样，则不增加功率就无法减少平均响应时间。 如果我们事先知道查询的大小，则可以尝试在内部重新排序，以减小 $$$A（吨）$ 和 $$$D（吨）$ 因此，平均系统响应时间。 继续这个想法，我们可以证明最短处理时间算法和最短剩余处理时间算法分别为一台服务器提供了最小的平均响应时间，而不会挤满它。 但是有一个副作用-可能不会无限期地处理大型请求。 这种现象被称为“饥饿”，并且与计划的公平性概念密切相关，可以从以前的计划工作岗位上学到：神话与现实 。

理解利特尔定律还有另一个常见的陷阱。 有一个单线程服务器可以处理用户请求。 假设我们以某种方式测量了L-该服务器在队列中的平均请求数，S-服务器处理一个请求的平均时间。 现在考虑一个新的传入请求。 平均而言，他看到L在他前面询问。 服务每个人平均需要S秒。 原来，平均等待时间 $$$W = L S$ 。 但是根据定理，事实证明 $$$W = L / \ lambda$ 。 如果我们将表达式等式，那么我们会看到废话： $$$S = 1 / \ lambda$ 。 这种推理有什么问题？

1. 引起您注意的第一件事：定理的响应时间不取决于S。实际上，它确实取决于S。 只是平均队列长度已经考虑了这一点：服务器越快，队列长度越短，响应时间越短。
2. 我们考虑的系统中，队列不会永远累积，而是会定期重置。 这意味着服务器利用率低于100％，并且我们跳过所有传入请求，并且以这些请求到达的平均速度相同，这意味着平均处理单个请求不会花费S秒，而是会花费更多 $$$1 / \ lambda$ 秒，仅仅是因为有时我们不处理任何请求。 事实是，在没有损失的任何稳定的开放系统中，吞吐量不取决于服务器的速度，它仅由输入流确定。
3. 传入请求在系统中看到的是时间平均请求数的假设并不总是正确的。 反例：传入的请求定期发送，我们设法在下一个请求到达之前处理每个请求。 实时系统的典型图片。 传入的请求在系统中始终会看到零个请求，但是平均而言，系统显然拥有多于零个请求。 如果请求是完全随机的，那么它们实际上是“看到请求的平均数量” 。
   
   
   
4. 我们没有考虑到服务器中可能已经有一个请求需要“扩展”的可能性。 在一般情况下，“售后服务”的平均时间与最初的服务时间有所不同，有时反而可能会更长。 当我们讨论微爆时，我们将在最后讨论这个问题，敬请期待。

因此，利特尔定理可以应用于大型和小型系统，队列，服务器以及单个处理线程。 但是在所有这些情况下，请求通常以一种或另一种方式进行分类。 不同用户的请求，不同优先级的请求，来自不同位置的请求或不同类型的请求。 在这种情况下，按类汇总的信息就没有意义。 是的，混合请求的平均数量和所有请求的平均响应时间再次成比例。 但是，如果我们想知道某类请求的平均响应时间怎么办？ 令人惊讶的是，利特尔定理可以应用于特定类别的查询。 在这种情况下，您需要 $$$\ lambda$ 此类请求的速率，不是全部。 作为一个 $$$L$ 和 $$$W$ -在系统的调查部分中此类请求的数量和停留时间的平均值。

开放式和封闭式系统

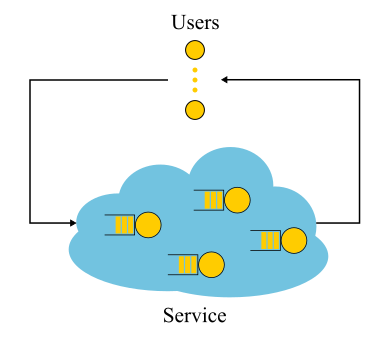
值得注意的是，对于封闭系统，“错误”的推理路线可以得出结论 $$$S = 1 / \ lambda$ 原来是真的。 封闭系统是这样的系统，其中请求不是来自外部，也不是外部，而是在内部循环。 或者，否则，是反馈系统：一旦请求离开系统，就会有一个新的请求代替。 这些系统也很重要，因为任何开放系统都可以视为浸入封闭系统中。 例如，您可以将网站视为开放系统，在其中不断请求，处理和撤回请求，或者相反，将其与网站的整个受众一起视为封闭系统。 然后，他们通常会说用户数量是固定的，他们要么等待请求的响应，要么“想”：他们收到了他们的页面，但还没有单击链接。 如果认为时间始终为零，则该系统也称为批处理系统。

如果外部到达的速度，则密闭系统的小定律是有效的 $$$\ lambda$ （它们不在封闭的系统中）替换为系统带宽。 如果我们将上述讨论的单线程服务器包装在批处理系统中，则会得到 $$$S = 1 / \ lambda$ 和100％回收。 通常，对系统的这种查看会带来意想不到的结果。 在90年代，正是互联网与用户作为单一系统的这种观点推动了对指数分布以外的分布的研究。 我们将进一步讨论分布，但是在这里我们注意到，那时几乎所有事物和地方都被认为是指数式的，甚至找到了一些理由，而不仅仅是“否则太复杂”精神的借口。 然而，事实证明并非所有实用上重要的分布都具有同样长的尾巴，因此可以尝试了解分布尾巴。 但是现在，让我们回到平均值。

相对论效应

假设我们有一个开放的系统：一个复杂的网络或一个简单的单线程服务器-没关系。 如果我们将请求的到达速度加倍并将处理速度提高一半（例如，通过将所有系统组件的容量增加一倍），将会发生什么变化？ 利用率，吞吐量，系统中平均请求数和平均响应时间将如何变化？ 对于单线程服务器，您可以尝试采用公式，在“额头上”应用公式并获得结果，但是如何处理任意网络？ 直观的解决方案如下。 假设时间加倍，那么在我们的“加速参考系统”中，服务器的速度和请求流似乎没有变化； 因此，加速时间中的所有参数都具有与以前相同的值。 换句话说，任何系统的所有“运动部件”的加速度等于时钟的加速度。 现在，我们将这些值转换为具有正常时间的系统。 无量纲数量（利用率和平均请求数）将保持不变。 其维包括一阶时间因子的值成比例地变化。 [requests / s]的吞吐量将加倍，并且响应和等待时间[s]将减半。

可以用两种方式解释此结果：

1. 以k倍加速的系统可以以k倍多的速度消化任务流，而以k倍的平均响应时间来消化任务流。
2. 可以说，能力没有改变，只是任务的大小减少了k倍。 事实证明，我们向系统发送了相同的负载，但被分割成较小的部分。 还有……哦，一个奇迹！ 平均响应时间减少了！

再一次，我注意到，这适用于各种系统，而不仅仅是简单的服务器。 从实际的角度来看，只有两个问题：

1. 并非系统的所有部分都可以轻松加速。 我们根本不能影响某些人。 例如，光速。
2. 并非所有任务都可以无限地划分为越来越小的任务，因为还没有学会将信息传输到少于1位的部分。

考虑通过极限。 假设在同一个开放系统中，解释号为2。我们将每个传入请求均分为两半。 响应时间也减半。 重复除法多次。 而且，我们甚至不需要更改系统中的任何内容。 事实证明，只需将传入的请求分成足够多的部分，就可以使响应时间任意缩短。 在极限范围内，我们可以说不是查询而是“查询流体”，它由服务器过滤。 这就是所谓的流体模型，它是简化分析的非常方便的工具。 但是为什么响应时间为零？ 怎么了？ 我们在哪里不考虑延迟？ 事实证明，我们不仅仅考虑光速，还不能将其提高一倍。 网络通道中的传播时间无法更改，只能忍受。 实际上，通过网络的传输包括两个部分：传输时间和传播时间。 第一个可以通过增加功率（通道宽度）或减小数据包的大小来加速，第二个很难影响。 在我们的“液体模型”中，没有用于储存液体的容器-具有非零且恒定传播时间的网络通道。 顺便说一句，如果我们将它们添加到“液体模型”中，则延迟将由传播时间的总和确定，并且节点中的队列仍将为空。 队列仅取决于数据包大小和输入流的可变性（读取突发）。

随之而来的是，在延迟方面，您无法进行流量计算，甚至回收设备也无法解决所有问题。 有必要考虑到请求的大小，不要忘记分发时间，尽管在计算中添加它并不困难，但在排队论中通常会忽略它。

发行版

排队的原因是什么？ 显然，系统没有足够的容量，并且过多的请求正在累积吗？ 不对！ 在有足够资源的系统中也会出现队列。 如果没有足够的容量，那么该系统就如理论家所说的那样不稳定。 排队的主要原因有两个：请求的不规则性和请求大小的可变性。 我们已经研究了消除这两个原因的示例：一个实时系统，其中相同大小的请求严格周期性地发出。 队列永远不会形成。 队列中的平均等待时间为零。 , , , . , .

A/S/k/K, A — , S — , k — , K — (, ). , M/M/1 : M (Markovian Memoryless) , . : $$$\lambda$ — — , : . M , μ . , , . , 4- . , , : G — (, , ), D — deterministic. C — D/D/1. , 1909 ., — M/D/1. — M/G/k k>1, M/G/1 1930-.

?

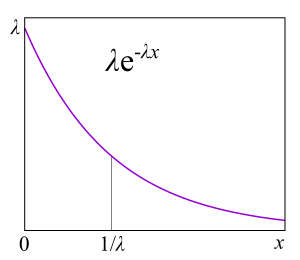
, , , , , . , . , failure rate . , , : , . failure rate function, . , «» , . , : , . , failure rate — , , - , — . , , , , , . « ».

Failure rate . — . Failure rate , , , . failure rate, , , . failure rate, , , . , , , software hardware? : ? . , , - . ? , — . ( failure rate) . « » .

, , failure rate, , , unix- . , .

RTMR , . LWTrace - . . , . , $$$\mathbf{P}\{S>x\}$ . , failure rate , , : .



$$$\mathbf{P}\{S>x\} = x^{-a}$ , — . , « », 80/20: , . . , . , RTMR -, , . $$$a=1.16$ , 80/20: 20% 80% .

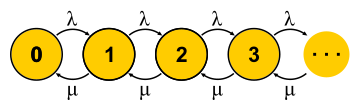
, . . , , , - . , — . « » , « » — . : , ? , ( , ), . , 0 . , , $$$\mu N_1$ $$$\lambda N_0$ 。 , , — . . , . M/M/1 $$$\mathbf{P}\{Q=i\} = (1 - \rho) \rho^i$ 在哪里 $$$\rho = \lambda / \mu$ -这是服务器利用率。 故事的结尾。 在介绍的过程中，我错过了大量的假设，并做了一些概念上的替换，但我希望本质不会受到影响。

重要的是要了解，这种方法仅在机器的当前状态完全确定其进一步行为的情况下才有效，并且关于如何进入此状态的故事并不重要。 对于每天对有限状态机的理解，这毋庸置疑-毕竟这是一个条件。 但是对于一个随机过程，由此得出的结论是，所有分布都必须是指数分布的，因为只有它们没有内存-它们具有恒定的故障率。

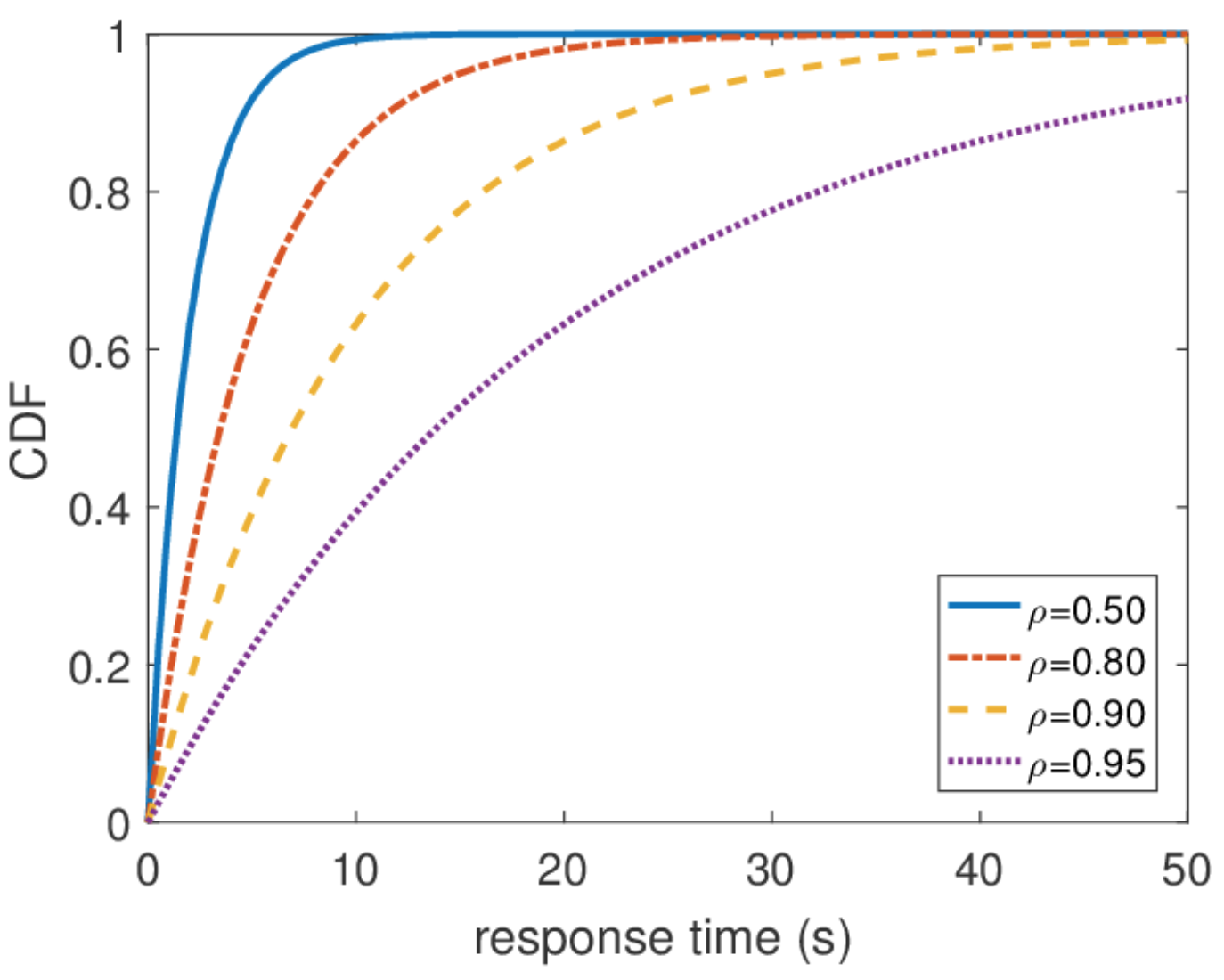
同样重要的是，如果我们知道平衡分布，则很容易获得有关系统的所有其他信息。 系统中的平均查询数量是该分布的平均值。 为了找出平均响应时间，我们将利特尔定理应用于查询数量。 响应时间的分布较难找到，但是通过一些操作，您可以发现 $$$\ mathbf {P} \ {响应\ _time> t \} = e ^ {-（\ mu- \ lambda）t}$ 什么是平均响应时间 $$$1 /（\ mu- \ lambda）$ 。

无限的响应时间

从这个分布中，您可以找到响应时间的任何百分位数，结果表明百分位数等于无穷大。 换句话说，最坏的响应时间不受上面的限制。 一般来说，这并不奇怪，因为我们使用了泊松流。 但是实际上，这种行为是永远无法实现的。 显然，到服务器的请求输入流至少受到到该服务器的网络通道的宽度的限制，并且队列长度受此服务器上的内存的限制。 相反，泊松流具有非零的概率，保证了任意大突发的发生。 因此，如果您对高百分位数感兴趣并且系统负载非常高，那么在设计系统时，我不建议您从泊松输入流的假设出发。 最好使用其他流量模型，这将在我谈论网络演算时再讨论。

缩放和保修

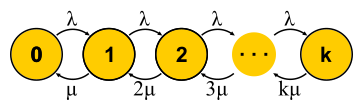
既然我们已经拥有足够强大的方法来分析系统，那么我们可以尝试将其应用于不同的任务并获得收益。 这就是大众服务理论在二十世纪下半叶发展起来的方式。 让我们尝试了解所取得的成就。 首先，让我们回到Erlang解决的任务。 这些是任务M / M / k / k和M / M / k，在其中我们要限制失败的可能性。 事实证明，构建马尔可夫链并不困难。 不同之处在于，随着任务的添加，反向转移的可能性增加，因为任务开始并行处理，但是当任务数等于服务器数时，就会发生饱和。 此外，对于M / M / k / k，网络结束，自动机实际上是有限的，并且所有到达最后一个状态的请求都被拒绝。 此事件的概率仅等于我们处于最后状态的概率。

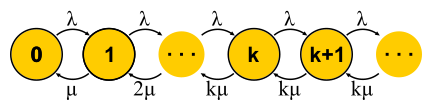
对于M / M / k，情况更加复杂，请求排队，出现新状态，但是反向转换的可能性并未增加-所有服务器都已在工作。 对于M / M / 1，网络变得无限。 顺便说一句，如果系统中的请求数量受到限制，那么链将始终具有有限数量的状态，并且将解决一种或另一种状态，这对于循环链来说是无法说的。 在封闭系统中，链始终是有限的。 求解描述的M / M / k / k和M / M / k的电路，我们分别得出公式B和Erlang 公式C。 它们相当笨重，我不会给他们，但是在它们的帮助下，您可以为直觉的发展获得有趣的结果，这称为平方根人员编制规则。 假设有一个M / M / k系统，每秒有一些给定的请求输入流λ。 假设到明天负荷应该增加一倍。 问题是：如何增加服务器数量，以使响应时间保持不变？ 服务器数量需要加倍，对吗？ 事实证明一点也不。 回想一下，我们已经看到：如果将时间（服务器和登录）速度缩短一半，那么平均响应时间将减少一半。 几台慢速服务器和一台快速服务器不是一回事，但是计算能力却是相同的。 特别是对于M / M / 1，响应时间与“自由容量”的数量成反比 $$$\亩-\ lambda$ 并且仅由该体积决定。 当流量和处理能力加倍时，系统的可用容量将增加一倍： $$$2 \亩-2 \ lambda$ 。 似乎要解决该问题，您只需要节省可用容量，但是响应时间（M / M / k）已经由更复杂的Erlang公式确定。 事实证明，必须与“繁忙服务器”数量的平方根成比例地维护可用容量，以保持相同的响应时间。 “繁忙服务器”的数量是指服务器总数乘以利用率：这是稳定运行所需的最小服务器数量。

有时，他们使用此规则尝试证明如何使用服务器扩展群集。 但是不要以为任何集群都是M / M / k系统都是一种幻想。 例如，如果您在输入端有一个平衡器，该平衡器将队列中的请求发送到服务器，则不再是M / M / k，因为M / M / k表示一个公共队列，服务器在释放请求时从该队列中提取请求。 但是此模型适用于例如具有公共FIFO队列的线程池。 但是，即使在这种情况下，也要记住，该规则是线程很多的情况的近似值。 实际上，如果您有10个以上的线程，则可以放心地假设其中有很多线程。 好吧，不要忘了普遍存在的指数分布：如果不假设所有分布的指数性，该规则也不起作用。

网络响应时间

最终，由于我们创建了分布式系统，因此有趣的是至少一个链状连接的M / M / k网络。 为了研究网络，我想要一个构造函数：将已知元素连接到块中的简单明了规则。 例如，在控制理论中，传递函数可以理解为与串行或并行连接相结合。 在这里，任何节点的输出流都有非常复杂的分布，M / M / k除外，根据众所周知的Burke定理， M / M / k会产生独立的泊松流。 您可能会猜到，该例外主要被使用。

两个泊松流的连接是泊松流。 泊松流一分为二的概率再次给出了两个泊松流。 所有这些导致这样一个事实，即系统中的所有队列似乎都是独立的，并且您可以用正式语言获得所谓的产品形式解决方案 。 也就是说，队列长度的联合分布只是所有队列长度分布的乘积，单独考虑-这就是概率论中表示独立性的方式。 我们只是找到流向所有节点的输入流，并分别对每个节点使用公式。 有许多限制：

1. 概率路由算法。 节点服务的请求以已知的概率随机选择下一个。 这并不像看起来那样糟糕，因为可以使用“请求类”：说所有Vasya的请求先到达1号服务器，然后到达2号服务器，然后出网络，然后Petya的请求到达2号服务器。 ，然后以相同的概率访问1号或3号服务器并退出。 也就是说，并非所有过渡都必须是随机的，某些甚至所有过渡都可能具有100％的概率。
2. 假设克莱因洛克（Kleinrock）的独立性。 请求处理时间不能取决于请求的历史记录或类别，而仅由服务器确定，并且当请求再次通过同一服务器时，每次都会对其进行随机选择。 实际上，无法设置将在不同服务器中使用的请求的大小，并且服务时间仅由服务器本身确定。 您也可以尝试解决此限制。 为此，通常使用概率路由，并进行循环以一定概率返回到同一服务器-就像它们重新启动请求一样。 我认为这是一个很奇怪的技巧，因为这样的请求会重新进入队列，并且不会立即执行，但是对于某些任务来说，这并不重要。
3. 泊松输入所有节点上的流量和指数服务时间。

杰克逊网络示例。

值得注意的是，在存在反馈的情况下，由于流动是相互依赖的，因此无法获得泊松流。 在反馈节点的输出处，还获得非泊松流，结果，所有流都变为非泊松流。 但是，令人惊讶的是，如果满足上述限制，所有这些非泊松流的行为与泊松流完全相同（哦，这是概率论）。 然后我们再次获得产品形式的解决方案。 这种网络称为Jackson网络 ，它们可以提供反馈，因此可以多次访问任何服务器。 还有其他的网络允许更多的自由，但是结果，关于网络的排队论的所有重要分析成果都在投入和产品形式解决方案中涉及了泊松流，这成为对此理论的批评对象，并在90年代导致其他理论的发展，以及实际需要什么分布以及如何使用它们的研究。

整个杰克逊网络理论的重要应用是IP网络和ATM网络中的数据包建模。 该模型非常合适：数据包大小变化不大，也不取决于数据包本身，仅取决于信道宽度，因为服务时间对应于数据包发送到信道的时间。 随机发送时间虽然听起来很疯狂，但实际上并没有很大的可变性。 此外，事实证明，在具有确定的服务时间的网络中，延迟不能大于类似的Jackson网络中的​​延迟，因此可以安全地使用此类网络从上方估计响应时间。

非指数分布

我讨论的所有结果都与指数分布有关，但我也提到实际分布是​​不同的。 感觉整个理论是完全没有用的。 这并非完全正确。 此外，有一种方法可以将其他分布集成到此数学设备中，几乎可以将任何分布都集成到其中，但这将使我们付出一些代价。 除了一些有趣的情况外，失去了以显式形式获得解决方案的机会，产品形式的解决方案以及构造函数都失去了：每个问题都必须使用马尔可夫链完全从头解决。 从理论上讲，这是一个大问题，但在实践中，它仅意味着数值方法的应用，并有可能解决更为复杂和接近现实的问题。

相法

这个想法很简单。 马尔可夫链不允许我们在一个状态内拥有记忆，因此所有过渡都应该是随机的，并且两个过渡之间的时间呈指数分布。 但是，如果将状态划分为几个子状态怎么办？ 如果我们希望整个结构保持马尔可夫链，并且我们确实希望这样做，则子状态之间的过渡必须仍然具有指数分布，因为我们知道如何求解此类链。 如果子状态是串联排列的，则通常将其称为相，并且将分区过程称为相方法。

最简单的例子。 请求的处理分为多个阶段：例如，首先，我们从数据库中读取必要的数据，然后执行一些计算，然后将结果写入数据库。 假设所有这三个阶段都具有相同的时间指数分布。 所有三个阶段的渡越时间在一起是什么分布？ 这是Erlang的发行版本。



但是，如果您进行了很多很多相同的简短阶段，该怎么办？ 在极限条件下，我们获得确定性分布。 也就是说，通过构建一条链，可以减少分布的可变性。

是否可以增加可变性？ 很简单 我们使用替代类别，而不是阶段链，随机选择其中一个。 一个例子。 几乎所有请求都可以快速执行，但是，一个巨大的请求到来的可能性很小，这需要很长时间。 这样的分布将降低故障率。 我们等待的时间越长，请求就越有可能属于第二类。



不断开发阶段方法，理论家发现，存在一类分布，您可以使用该分布精确地求解任意非负分布！ 考克斯的分配是通过阶段法建立的，仅不需要我们经历所有阶段，在每个阶段之后都有完成的可能性。



这种分布既可以用于生成非泊松输入流，也可以用于创建非指数服务时间。 例如，这里是M / E2 / 1系统的马尔可夫链，具有服务时间的Erlang分布。 状态由一对数字（n，s）确定，其中n是队列的长度，而s是服务器所在的阶段的编号：第一或第二。 n和s的所有组合都是可能的。 传入消息仅更改n，并且在阶段完成后，它们交替出现并在第二阶段完成后减小队列的长度。

你有爆裂！

加载一半容量的系统能否减慢速度？ 作为第一个测试对象，我们准备M / G / 1。 给出：入口处的泊松流和任意分配的使用时间。 考虑单个请求在整个系统中的路径。 随机传入的请求在自己前面的队列中看到请求的平均时间数 $$$\ mathbf {E} [N_Q]$ 。 他们每个人的平均处理时间 $$$\ mathbf {E} [S]$ 。 等于处置的概率 $$$\ rho$ ，服务器中还有另一个请求，必须首先及时“服务” $$$\ mathbf {E} [S_e]$ 。 总结一下，我们得出队列中的总等待时间 $$$\ mathbf {E} [T_Q] = \ mathbf {E} [N_Q] \ mathbf {E} [S] + \ rho mathbf {E} [S_e]$ 。 利特定理 $$$\ mathbf {E} [N_Q] = \ lambda \ mathbf {E} [T_Q]$ ; 结合起来，我们得到：

$$

$$\ mathbf {E} [T_Q] = \ frac {\ rho} {1- \ rho} \ mathbf {E} [S_e]$$

即，队列中的等待时间由两个因素确定。 第一个是服务器利用率的影响，第二个是平均售后服务时间。 考虑第二个因素。 请求到达某个点 $$$t$ ，看到善后需要时间 $$$S_e（t）$ 。



平均时间 $$$\ mathbf {E} [S_e]$ 由函数的平均值确定 $$$S_e（t）$ ，即三角形的面积除以总时间。 显然，我们可以将自己限制在一个“中间”三角形，然后 $$$\ mathbf {E} [S_e] = \ mathbf {E} [S ^ 2] / 2 \ mathbf {E} [S]$ 。 这真是出乎意料。 我们已经收到，售后服务时间不仅取决于服务时间的平均值，还取决于其可变性。 解释很简单。 掉入长时间间隔的可能性 $$$S$ 此外，它实际上与该间隔的持续时间S成正比。 这解释了著名的“等待时间悖论”或“检查悖论”。 但回到M / G / 1。 如果您结合我们获得的所有内容并使用可变性进行重写 $$$C ^ 2_S = \ mathbf {E} [S] / \ mathbf {E} [S] ^ 2$ 得到著名的Pollaczek-Khinchine公式 ：

$$

$$\ mathbf {E} [T_Q] = \ frac {\ rho} {1- \ rho} \ frac {\ mathbf {E} [S]} {2}（C ^ 2_S + 1）$$

如果证明让您感到厌烦，我希望它能使实际应用的结果满意。 我们已经在RTMR中检查了服务时间数据。 长长的尾巴变化很大，在这种情况下 $$$C ^ 2_S = 381$ 。 您所看到的不仅仅是 $$$C ^ 2_S = 1$ 用于指数分布。 平均而言，一切都非常快： $$$\ mathbf {E} [S] = 263.792μs$ 。 现在假设RTMR是由M / G / 1系统建模的，并且让系统不被重载，丢弃 $$$\ rho = 0.5$ 。 代入公式，我们得到 $$$\ mathbf {E} [T_Q] = 1 *（381 + 1）/ 2 * 263.792μs= 50 ms$ 。 由于微爆，即使是这样一种快速且未充分利用的系统，平均而言也可以变成令人作呕的系统。 在50毫秒内，您可以访问硬盘驱动器6次，或者，如果幸运的话，甚至可以访问另一大洲的数据中心！ 顺便说一下，对于G / G / 1，有一个近似值考虑了传入流量的可变性：它看起来完全一样，只是相反 $$$C ^ 2_S + 1$ 这是两个品种的总和 $$$C ^ 2_S + C ^ 2_A$ 。 对于多台服务器，情况会更好，但是多台服务器的效果仅影响第一个因素。 可变性的影响仍然存在： $$$\ mathbf {E} [T_Q] ^ {G / G / k}≈\ mathbf {E} [T_Q] ^ {M / M / k}（C ^ 2_S + C ^ 2_A）/ 2$ 。

微爆发看起来像什么？ 关于线程池，这些任务的服务速度足够快，以至于在回收计划中不可见，而速度又很慢，足以在它们自己后面创建队列并影响池响应时间。 从理论上讲，这些都是从分布的尾部开始的巨大查询。 假设您有一个包含10个线程的池，然后查看基于运行时间和停机时间的指标的回收计划，该指标每15秒收集一次。 首先，您可能根本没有注意到一个线程正在挂起，或者所有10个线程同时执行大型任务一秒钟，然后在14秒钟内什么也不做。 15秒的分辨率不允许看到高达100％的利用率跃升至0％的跃迁，并且响应时间受到影响。 , , 15 6 , .



, ( ) .

, RTMR SelfPing, ( 10 ), — . , 10 15 . , . , , 10 , , — . self-ping- CPU. , : , , . : , , . : . , 15- , — .

, , SelfPing , ? ? , LWTrace. , . -100 . . : ; — , , ; perf , , .

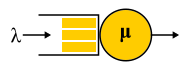
« », . , , . FIFO-. , , latency ( SPT SRPT). — . , , , . , « », .

, - product-form solution . M/ Cox /1/ PS . , (Coxian distribution) (Processor Sharing), , , . ? , . , , (. ) , , M/ M /1/ FIFO , , .

! , , , ! insensitivity property. , , , , . — M/M/∞. , . , product-form solution — BCMP .

. , (, ), , , ó . . 解决方法。 $$$\mathbf{E}[T] = 1/3 \mathbf{E}[T_1] + 2/3 \mathbf{E}[T_2]$ 。 $$$\mathbf{E}[T_i] = 1/(\mu_i - \lambda_i)$ M/M/1/FCFS $$$\mathbf{E}[T] = 1/3 * 1/(3 - 3 * 1/3) + 2/3 * 1/(4 - 3*2/3) = 0.5$ 。

, , . , .

1. , , , computer science, . Performance Modeling and Design of Computer Systems: Queueing Theory in Action (2013). - , . ó — .
2. , , , , Robert B. Cooper. , .