幸福理论。 事故不是偶然的吗？

我继续让哈勃（Habr）的读者熟悉他的著作《幸福理论》（Theory of Happiness）中的章节，并附带“中庸之道的数学基础”。 这本尚未出版的流行科学书，非常非正式地讲述了数学如何使您以新的认识水平看待世界和人们的生活。 它适用于对科学感兴趣的人和对生活感兴趣的人。 而且由于我们的生活是复杂的，而且总体上是不可预测的，因此本书的重点主要放在概率论和数理统计上。 这里没有证明定理，也没有给出科学的基础知识，这绝不是教科书，而是所谓的娱乐科学。 但是，正是这种几乎好玩的方法，使我们能够发展直觉，为学生提供生动的例子来丰富讲座，最后向非数学家和我们的孩子解释我们在干科学中发现的如此有趣。



在本章中，我们讨论预定的硬币飞行，地形图，数学灾难以及随机性。 在此过程中，让我们看一下诸如测度理论和动态混沌理论之类的数学部分。

关于日常活动动荡的卑鄙定律的讨论通常始于著名的三明治定律 。 它的配方简单，易于验证且广为人知：

三明治总是把黄油滴下来。

显然，这里的“始终”一词是一种夸张。 容易想象三明治会掉落的情况，而涂油的一面完好无损。 人们对这项法律有什么了解？ 三明治很可能经常掉下来使黄油变得引人注目。 但是，下跌的不利结果是否比下跌的可能性更大？ 三明治是不同的，它们处于不同的环境中，处于不同的高度。...有太多的参数，因此谈论此类任务中的模式可能毫无意义。 什么都可能发生。 碰巧它掉进了油里，然后变得侮辱人了，我们记住了法律，也记住了它。 而且，如果三明治变得不那么有趣-随着加油，或者事实证明根本没有加油，那就没什么可谈的了-很明显，法律是可笑的！ 最后，三明治就像一枚硬币，数学家用来获得具有两个可能值的随机变量：“鹰”和“尾巴”。 如果硬币是“诚实的”，那么倒下哪一侧绝对不重要，我们说老鹰和尾巴掉落的可能性是相同且相等的 $$$1/2$ 。 理论上，三明治应该相同。 我们将在下一章中再次讨论它们，但是现在让我们看一下最可能的简单概率系统-代币。

概率理论实验中的硬币以某种特殊的魔术方式抛掷，因此抛掷过程中初始位置，初始速度和旋转速度的选择不会影响特定结果的概率。 但这显然是不可能的！ 硬币是一个机械系统，遵循机械定律，但它们不包含随机变量。 像硬币这样的简单物体的运动定律的未来唯一地取决于该物体的过去状态。 如果机器人掷硬币，或者拉普拉斯恶魔是具有完全有关任何机械系统的坐标和速度信息的神话生物，那么使用恒定的初始数据将获得相同的结果。 我们当然不是机器人或恶魔，但是人们真的会把硬币扔得如此草率和不可预测，以至于机械定律可能导致事故吗？

一般说来，随机性来自力学定律所描述的世界吗？ 随机来自何处？ 真正混乱或随机的系统（根本上是不可预测的）与仅难以猜测行为但可以计算出行为的系统之间有什么区别？

1986年，约瑟夫·凯勒（Joseph Keller）考虑了硬币问题。 根据凯勒（Keller）文章的推理，我们提供了对此过程中不确定性发生的简单解释。 硬币落在哪一侧取决于其飞行时间。 $$$t$ 从角速度 $$$\ omega$ 。 如果以每单位时间的转数来测量角速度，则硬币产生的转数可以非常简单地表示 $$$n = t \欧米茄$ 。 这种依赖性在坐标系中设置了相等转数的线 $$$（t，\ omega）$ ，进而限制与偶数和奇数转数相对应的区域。

该图显示了飞行中的硬币执行的转数的奇偶性。 矩形显示最常发生硬币算命过程的区域。

在这样的图中，可以显示硬币翻转的结果是什么，每秒扭曲已知的转数，并在已知的翻转时间之后被捕获。 如果我们掉入一条白色的条带，那么折腾的那一面将掉落在上面，如果是橙色，则相反。 等速线是双曲线，可以看出，随着速度的增加，区域的交替变得越来越频繁，区域本身也变薄。 人的手是不完美的，很小的初始值散布一次覆盖了许多区域，从而导致结果不可预测。 在手的范围内（图中的矩形），偏移足够 $$$5 \％$ 从白色条纹跳到橙色。 问题仍然存在：这种构造如何遵循真正的机械硬币的“诚实性”？ 如何从结果图中获得丢失鹰或尾巴的可能性？

紧急采取行动！

为了更好地理解我们正在讨论的内容，我们将投入一些在学校没有教授的数学。 我们在引言中说过，数学家不会学习数字或几何形状，就像在学习一门学校课程后看起来的那样。 它们处理数学结构（抽象的代数，半环，场，monoid，拓扑空间和其他抽象的东西），似乎对它们进行了描述，但完全不涉及实践，定义它们，研究它们的性质，证明定理。 然后，他们磨练在各种知识领域中找到这种结构的技能，从而取得了令人惊奇的有用突破，包括在纯应用领域中的突破。 现在，我们将稍微介绍一下此类数学，并考虑如何基于非常抽象的度量概念来构建概率理论基础。

我们描述了硬币的力学原理，并获得了描述具有某些属性的解决方案集的区域。 区域是平坦的图形，如何正确地从它们移动到概率？ 我们需要衡量我们的区域，我们自然会来到他们的区域。 面积-是平面图形的度量 。 这是将集合与某个非负数值相关联的函数的精确数学术语。 度量的示例是枚举集中的数量（例如，袋子中的苹果数量）以及数字的长度 ， 面积和体积 。

在数学中有一整节叫做测量理论 。 这个理论诞生于19世纪和20世纪之交（Emil Borel和Henri Lebesgue起源于此），为数学家提供了分析Cantor和分形集等非常复杂的对象的机会。 它构成了功能分析和现代概率论的基础，而这一基础是由杰出的俄罗斯数学家安德烈·科尔莫戈洛夫（Andrei Kolmogorov）奠定的。 概率定义作为一种度量，使您可以查看离散集和连续集的概率的所有基本属性。

尽管我们的书不是教科书，但值得停下来从鸟瞰的角度看一下probability概率的概念，并体会一下数学的味道。 首先，我们列出了所有度量的主要属性。 为了更好地想象它们，可以使用“数量”或“长度”或“区域”一词代替“度量”一词。

1.空集的度量为零。
2.对于有限度量，整个可测量集的度量是有限的。
3.子集的度量不超过集合的度量
4.两个任意集合的并集度量等于这两个集合的度量之和减去它们相交的度量（可加性）。
5.补充子集的度量等于整个集合的度量与子集的度量之间的差。

可以使用任何非负数值函数作为度量吗？ 一点也不。 例如，年龄给一个人一个完全特定的数字。 但是两个人的年龄不能定义为他们的年龄之和。 跑步速度不是衡量标准-两个人的跑步速度不是两倍。 但是动量（动量）或能量已经具有度量的性质。 重量，金钱，知识量，哭声的量，虽然不总是容易衡量的，但也可以作为许多人的衡量标准。

在直觉上，几乎每个人现在都熟悉概率的概念。 政治学家和记者在脱口秀节目上估计，有人谈论全球变暖或明天下雨，有人开玩笑说： 在特维尔遇到恐龙的可能性是多少？ -一秒钟：是否开会。 在现代数学中， 概率的概念定义为对称为概率空间的特殊集合的度量。 它包括基本事件及其使用并集，交集和排除操作获得的组合。 基本事件的一个示例：“投掷骨头时损失三倍”。 非基本事件的一个示例：“除两个以外的任何偶数的丢失”。 因此，我们列出了概率的属性：

1.不可能发生的事件的可能性为零。
2.整个概率空间的概率等于1。
3.如果一个事件也需要另一个事件，则第二个事件的概率不会超过第一个事件的概率。 在这里，事件的“需求”关系等同于集合的“是子集”，并不意味着“是原因”。
4.两个任意事件中至少一个发生的概率等于这些事件中每个事件的概率之和，减去事件同时发生的概率。
5.事件未发生的概率为一减去事件发生的概率。

仔细研究度量和概率的属性，您将看到我们在谈论相同的属性。

并非概率的所有性质都来自其对度量的定义：事件的独立性概念以及通过条件概率引入概率乘积同时计算两个或多个独立事件的概率的方法 ，但是这些概念与Kolmogorov定义一致。

离散随机变量对应于有限可数集；在其中，自然度量是元素数量的普通计数。 因此，离散概率空间中的概率是每个学生都熟悉的选项的组合计算。 对于连续随机变量，概率作为度量，更像是长度或面积，在这里我们谈论的是概率密度 。

与测度的概率类比不止于此。 平均值是多少？ 这类似于由点质量或已知密度的实体组成的图形的质心位置 。 这些数量的计算方法相同。 随机变量在平均数附近的分散如何表征： 方差 ？ 就像惯性矩可以表征质心周围的质量分布一样。 再次，用于计算样本或分布的方差的公式与用于一组狡猾形状的实体或实体的惯性矩的公式一致。

顺便说一句，如果我们在概率的定义和性质中用“最大值”代替总和，而用“最小”代替乘积，那么我们可以构建一个替代理论，称为可能性理论 。 这就是数学的原理。 我们从抽象推理开始：数字构成一个具有加法和乘法运算的代数，但是在有限的数区间上，您可以构建一个具有最小和最大运算的相似代数。 我们在新的代数上建立度量的概念，并发现它打开了世界的新视野！ 与概率论相反，在这种理论中，可以构造两个协调的度量- 可能性和必要性 ，并且与概率不同，它们与合并事件和相交事件的操作都非常一致。 这个方向是由阿塞拜疆人American Lotfi Zadeh最初创建的，它是模糊逻辑的基础，并用于自动模式识别和决策系统。

令人难以置信，但却是事实！

量度的第一个特性看似微不足道，但它的不对称性很有趣。 如果子集的度量为零，则并不意味着它为空！ 例如，一条线是平面上点的子集，但其面积（度量）为零。 还有更多奇特的例子-具有复杂结构的Cantor和分形集，包含无数个点，显然“占据”了某个面积或体积，但是零度量值。

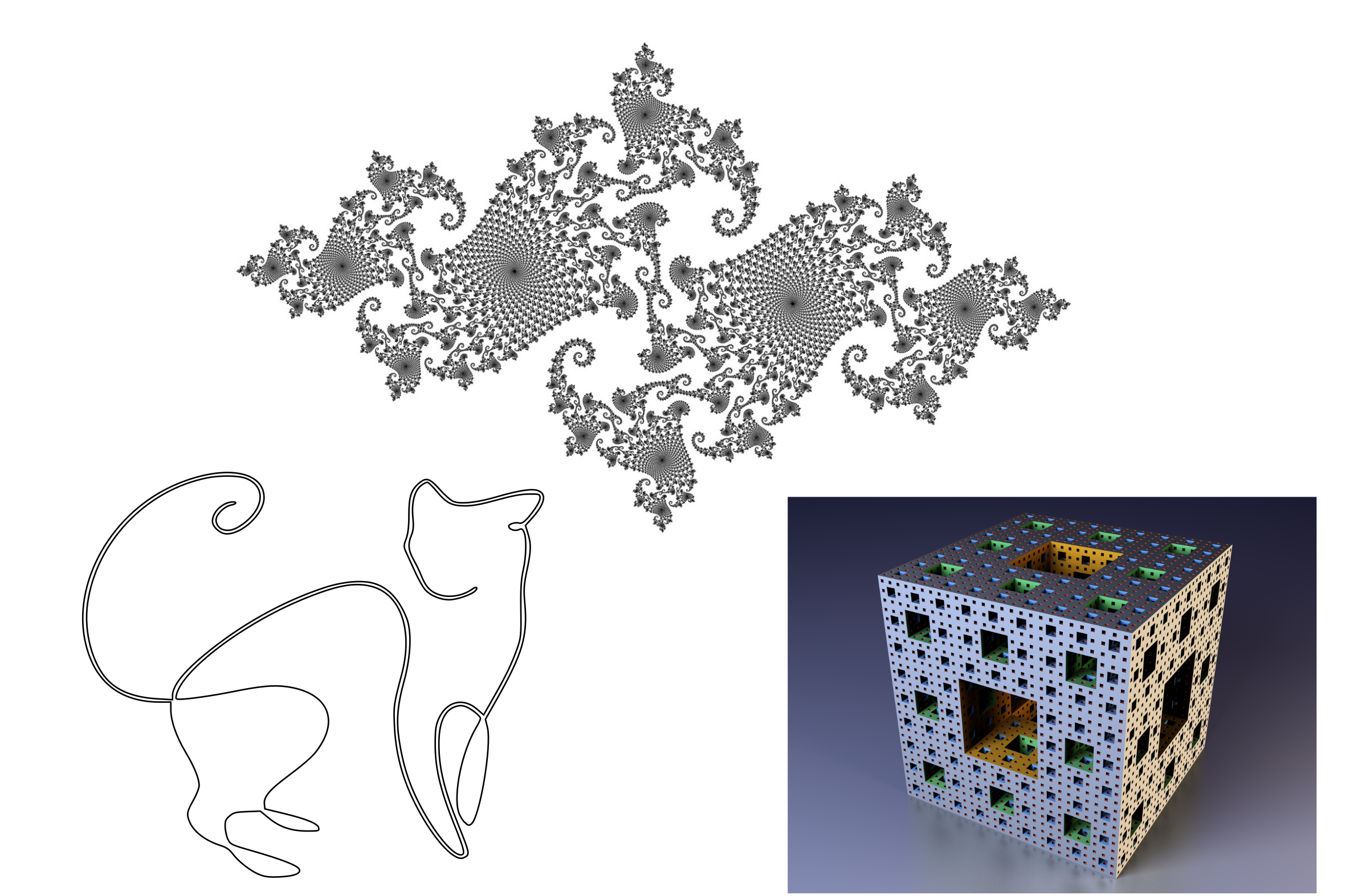零度量的一些对象：平面上的线，零星的Julia集，Menger分形海绵。

在准备此插图时，我在高分辨率的透明背景上发现了朱莉娅断开连接的一组奇妙图像。 将其插入矢量编辑器后，我遇到了一个有趣的难题-用鼠标选择该图像非常困难。 它是如此“松散”，以至于进入填充像素的可能性明显小于进入透明背景的可能性。 在概率空间中，零度量的子集也可能存在，但这并不意味着来自这些子集的事件是不可能的。 从第四次到第五次尝试，我仍然可以选择图像，因为像素的大小是有限的。 但是，如果我可以支配无限分辨率的真正不连贯的朱莉娅集，将会发生什么？

假设您正在使用一个软件随机数生成器，该生成器可以从 $$$0$ 之前 $$$1$ 。 数字掉出的概率是多少？ $$$0$ ？ 和数字 $$$1/2$ 或 $$$e / \ pi$ ？ 在所有这些情况下，答案都是-零！ 而是计算机可以使用的最小的正数，即所谓的机器epsilon，因为计算机以有限的小数位数运行。 等一下，您说的是什么意思零？ 相同的数字并非不可能。 让我们进行一个实验，结果得到一个特定的数字，当我们得到它时，“通过构造”它出现的可能性不能为零。 没错，但是我应该等多久才完全退出0？ 几乎是永无止境！ 事实是，单个数字（如线段上的点）具有零度量和诚实的零概率。 只有连续段的度量（甚至很小的）都不为零。 因此，我们不是在谈论概率，而是在谈论概率密度，当概率密度乘以概率空间中子集的有限度量时，将得出一个有限值-落入该子集的概率。 顺便说一句，证明它是我们无限精确的理想随机数生成器，用它获得某个有理数（不是一些具体的，但有的）的可能性也将为零。 在19世纪末，有理数形成了实数集的零度量的密集子集的证明引起了争议。

如果有人耐心地用一枚硬币进行了上千次实验，并高兴地告诉您，他得到的“鹰”和“尾巴”一样多，那么您可以放心地表示怀疑或祝贺他的运气不佳。 尽管抛硬币和离散的随机过程，但随着统计数据的累积，概率空间的力量将增加，并且事件的度量标准：“老鹰”的数量与“尾巴”的数量一致。 使用斯特林公式可以证明，随着测试次数的增加，该“最可能”事件的概率趋于零。 $$$1 / \ sqrt {\ pi n}$ 。 对于一百个演员表，这是百分之五多一点，一万个-只有百分之五。 在这种情况下，数学家说： 几乎可以肯定，“鹰”的数量将不等于“尾”的数量 。 不管听起来多么奇怪，但“几乎可以肯定”是一个精确的数学术语，这意味着该事件是零度量概率空间子集的补充。 当我们问自己时，我们将在以下各章之一中回到这些考虑：每个人中有多少人可以认为自己是正常的。

检查真实硬币的诚实性

让我们回到硬币及其诚实性上。概率的Kolmogorov定义使频率定义（作为发生事件的相对频率）与几何定义（在可能性的总“体积”中占事件“体积”的一部分）一致。因此，图中为旋转硬币计算出的白色条纹区域的分数反映了我们抛掷硬币的同一侧掉落的可能性。

但是麻烦！图中每个条带的面积是无限的（如果考虑坐标平面的四分之一）。但是，该度量的可加性将使我们能够准确地表明，这不会阻止阴影区域和白色区域的面积相同。以显式形式，我们曲线的方程式为$$$\omega = n/t$ 。 如果曲线下面积 $$ω = 1 / t等于$\omega = 1/t$$$S，则由于可加性，曲线下的面积$S$$$ω = n / t等于$\omega = n/t$$$$S_n = n S$ 。 反过来，对于单个条，我们得到： $$$S_{n} - S_{n-1} = n S - (n-1)S = S$ 。事实证明，面积的差异不取决于双曲线的“数量”。对于双曲线这不是什么特别的事情；对于任何形式的曲线都可以得出相同的结论$$y = n f （x ）（仅函数）$y = n f(x)$$$f是可测量的。如果是这样，那么对于整个定义区域，也有可能进入图表的白色部分或阴影部分，就像“诚实”硬币所期望的那样。我们刚才引用的论点看起来很简单，但是它们给出了非常普遍的结果，适用于任何加法量。度量的抽象概念使我们可以比较无休止的数量，同时保持在逻辑和常识的框架内。抽象是好的，但是可以说，实际上我们并不是在抛掷所有可能参数的硬币。如使用高速相机进行的实验所示，角速度在$f$



$$20至$20$$$每秒 40转，飞行持续时间从一半到一秒。该区域在图中以矩形突出显示。在其中，白色条纹的总面积略大于橙色条纹的总面积，我们可以得出结论，抛掷时掉出同一侧的概率为$40$$$$50.6\%$ 。

2007年，斯坦福大学的Percy Deaconess等人发表了一篇文章，提供了抛硬币过程的详细分析。详细描述飞盘和旋转盘的力学原理，旋转盘不仅旋转而且还进动-旋转轴本身在飞行中旋转，显示出在从“鹰从上方”位置手动抛掷时，“鹰”掉落百分之一百的可能性大于一半。

是很多还是一点？您需要进行多少次实验才能发挥作用？随着实验数据的积累，平均值的标准误差（反映可以计算平均值的误差）与测试次数的平方根成比例地减小：$$σ μ = σ / √ñ，在这里$\sigma_{\mu} = \sigma/\sqrt{n}$$$σ是研究分布的标准偏差。在我们的案例中，对于伯努利分布，概率$\sigma$$$0.51等于$0.51$$$$\sqrt{0.51\times0,49}\approx0.5$ 。 为了自信地确定平均值的百分之一的偏差，该偏差应 $$3个标准差。因此，我们可以估计试验次数：$3$

$$

$$n = \left(\frac{\sigma}{\sigma_{\mu}}\right)^2 = \left(\frac{3\times0.5}{0.01}\right)^2 \approx 22500$$

如此多次，您需要掷硬币来注意结果的机械预先确定。为了更清楚地说明其含义，我将举一个例子进行两次200次理想和稍微不完美的“硬币”测试，以计算损失例如老鹰的可能性。每个测试包括$$40,000次抛掷 单词“ coin”和“ tossing”都用引号引起来，因为实际上并没有使用物理硬币，而是服从伯努利分布的随机数生成器。$40000$

尝试扔出理想的，稍有瑕疵的硬币以修复瑕疵。

可以看出，只有在$$观察到的平均值“云”的 20,000个测试开始明显分开。好吧，对于家用，我们可以假设硬币是随机产生的两个相等可能性选项的良好生成器。$20000$

旅游法

概率的几何和频率确定的等价揭示了均值定律的奥秘，在旅行者，地质学家和所有使用地形图的人中都知道：

游客去的地方通常是在地图的折页上或在图纸的边缘上。

假设我们同样经常对位于地图所有部分的对象感兴趣。但是我们很少对零度量的对象感兴趣-使用地图的全部目的是调查对象的周围环境，即某个有限区域。让一小部分对我们来说足够了$$整个地图区域中的 α$\alpha$$$S弄清楚如何到达对象。因此，如果物体在某个临界距离处接近弯曲或边缘$S$$$d，我们将考虑遵守旅游法。边界区域在地图总面积中所占的份额将使我们有机会体验自己的卑鄙定律。这就是地图上令人不快的部分看起来的样子$d$$$α = 0.5 ％，一转弯。$\alpha=0.5\%$

灰色表示“坏”区域。分别示出了卡宽度40厘米的半点区域的一部分，它有一个直径略大于3厘米。

对于方形卡$$$d = \sqrt{\alpha S}$ 。 不愉快的小条将有一个区域 $$$d \sqrt{S} = S\sqrt{\alpha}$ 。四个条纹（两个垂直和两个水平）将位于边缘，任何附加的弯曲（水平或垂直）将添加另一个条纹。同时，相交的条带会在面积上增加额外的正方形$$$d^2 = \alpha S$ 。 通过折叠卡使其原来 $$$n$ 水平和 $$$m$ 垂直弯曲，我们得到的不愉快区域的总面积等于： $$$S（n + 2）\ sqrt {\ alpha} + S（m + 2）\ sqrt {\ alpha} -S（n + 2）（m + 2）\ alpha$ 。 将其带到整个地图的区域，我们在总区域中得到了不愉快的份额：

$$

$$p =（n + m + 4）\ sqrt {\ alpha}-（n + 2）（m + 2）\ alph$$

该图显示了该比例超出的区域 $$$50 \％$ 各种价值 $$$\ alpha$ 。

处于地图折叠处或其边缘的可能性增加的区域。 数字表示所考虑的邻域的面积占整个地图面积的比例。

事实证明，对折成两半的卡已经正式被认为相对于游客而言是不诚实的。 多数情况下，纸牌具有三个垂直折叠和三个水平折叠，这使满足均值律的概率为 $$$60 \％$ 在 $$$\ alpha = 0.5 \％$

机会从何而来？

在纪念品商店中，您可以找到“需求选择”的磁性摆锤。 它们也是机械随机发生器，有时被错误地称为“混沌摆”。 从某个初始位置和速度开始运动，摆进行一系列“不可预测的”振荡，最后在一个扇区中停止。 但是，这里的波动并不是不可预测的，它们对初始条件非常敏感。 对于摆锤可以停止的每个扇区，在坐标速度空间中都有一个吸引区域 。 这是一组这样的初始条件，在这种条件下，摆必定会吸引到指示扇区中的某个点。 摆的停止点称为吸引子 -吸引点。 在图片为钟摆的情况下，坐标和速度的空间是四维的，因此显示吸引区域并不容易。 但是，如果我们仅将自己限制在两个扇区，并将问题简化为一维（这样的摆称为Duffing振子），那么初始值的空间将变成一个平面，从而可以看到吸引区域。 它们看起来像是复杂的阴阳符号，很快变成狭窄的条带，将吸引人的区域分开。

一维欲摆吸引子的吸引区域-Duffing振子。

就像硬币一样，稍微改变初始条件，我们就从一个吸引子变成了另一个吸引子。 骰子和轮盘赌的工作方式相同，但它们本身并不是随机生成器。 这些不是真正的混沌系统，可以准确地计算其行为。

但是真正的机会是什么？ 真正的随机系统的一个很好的例子是汽车在道路上的出现。 人们不同意，不协调他们的计划，道路之外的合奏的每个元素都独立发挥作用。 尽管人们的行为有某些规律-早上和晚上的高峰时间，晚上的空旷道路等，但我们没有并且永远也不会获得有关运动中每个参与者的足够信息来预测其中任何一个的出现。 量子水平的基本粒子的力学，不稳定原子的衰变，遗传密码的变化，最有可能的是地震和证券交易所的股票报价也是随机的。 对于研究人员而言，唯一剩下的就是将它们视为随机变量，并根据概率论对其进行描述。

但是，还有另一种机会源- 动态混乱 。 混沌系统与随机系统的不同之处在于，它们由不包含随机性的精确方程和参数来描述。 但是，它们的行为不仅复杂，而且混乱而且确实不可预测。 如果我们开始非常仔细地在欲望和钟摆上以精确控制的频率和幅度振荡，我们将发现它的平稳运动无法长时间计算。 在任意精确的计算机上，没有任何算法可以让我们为任意遥远的未来计算摆的确切行为。 他不会停在任何扇区，但会平稳移动，但永远不会两次回到坐标速度空间中的同一点。 极其简单的混沌系统的另一个示例是理想球在弹簧上的理想桌子上的重力场中弹跳。 相对简单的洛伦兹方程式表明，我们永远无法预测超过两周的天气-这也是一个混乱的系统。

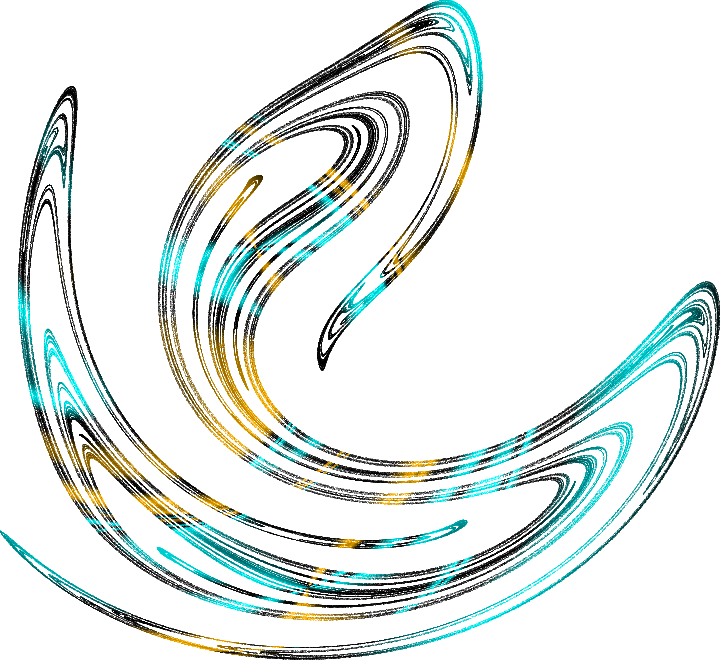
动态混沌理论能够解释这种不可预测性的本质。 我们检查了一个简单的一维欲望钟摆，它有两个稳定的固定点-两个吸引子，一个不稳定的点，系统试图摆脱这个不稳定点，用白色圆圈表示。 在混沌模式下，系统中出现了无数个不稳定的静止轨迹，而不是一组吸引子。 这个集合是无限的，但是度量为零 ，并且是一个非常复杂的不相交的结构。 一旦在这些轨迹之一上，原则上就不可能使用任何有限算法来跟踪它。 但最令人惊讶的是，事实证明，这种无限数量的不稳定轨迹本身具有吸引力！ 混沌系统从一个不稳定的轨迹附近连续跳到另一个轨迹，同时始终保持在这个奇怪的吸引子的范围内。 因此，这些集合称为： 奇怪的吸引子 。 这就是一个奇怪的吸引子部分，由于欲望的摆幅，容易受到谐波振荡的影响，看上去如此迷人。 一维摆的目的可以在三维空间（坐标，速度，强制振荡的相位）中描述。 如果用飞机在该空间中切开一个吸引子，则可以看到其结构，这称为庞加莱截面 。 这里的每个点都是轨迹的迹线，点的颜色反映了轨迹彼此散射的相对速度。 这是几个美丽的奇怪吸引子：


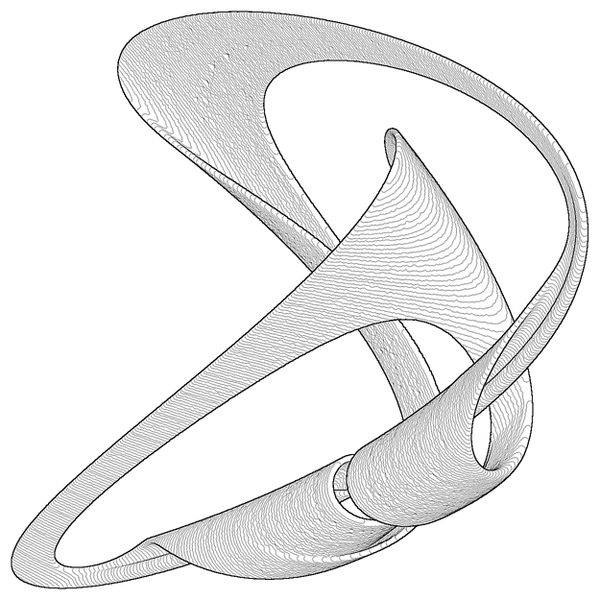左：庞加莱部分，显示弹跳弹簧的球在弹跳时的弹道。 许多点属于与能量守恒定律相对应的球体表面。 右：包围厚板强迫振动时产生的奇怪吸引子的体积区域。

混沌轨迹的平滑度使您可以展望未来。 这解释了一个令人讨厌的观察结果：一方面，天气预报员有时无法自信地预测一周的天气，但另一方面，如果您说明天将与今天相同，那么在四分之三的情况下，您不会被误认为。 通常，关于天气预报员的笑话是不公平的，我们必须赞扬人类的思想和毅力，这使人们有可能在现代水平上预报天气！

从理论上讲，动态混乱非常复杂且美丽，它可以产生令人赞叹的优雅影像，但它也很有用。 例如，计算机中用来生成随机数的算法也是确定性的。 对于本书中的示例，我使用了一个伪随机数生成器，该生成器没有启动真正的随机过程（alpha衰减或对道路上的汽车进行计数），而是根据之前接收到的先前的数字来计算下一个“随机”数。

从硬币到蝴蝶再到命运本身

观察到微小的偏差如何演变为系统的整体变化，导致人们想到了“蝴蝶效应”。 让我提醒您，这种影响意味着一系列微不足道的乍看起来会产生深远的戏剧性后果。 雷·布拉德伯里（Ray Bradbury）的短篇小说《和雷击》中的蝴蝶被过去的研究人员所压倒，从而彻底改变了未来。 动态混乱理论的创造者爱德华·洛伦兹（Edward Lorenz）的演讲之一是：“巴西蝶形翅膀的襟翼会在德克萨斯州引发龙卷风吗？”

我们隐含地提及这种影响，并感叹：“如果我不转弯，一切都会有所不同！”，“如果他没有登上这列火车，就不会有灾难！” 或“由于这样的琐事，他们吵架了！” 但是，我们看到，一个真正的随机量子世界和超精密原子钟共存，在恒星和星系世界以及土星环或柯伊珀环的混乱，分子的热运动以及生物系统或汽车机制的惊人运行精度中都存在着稳定的哈密顿系统。 不，蝴蝶翅膀的襟翼不会引起飓风，但是会消失得无影无踪，从而产生一连串的涡旋，将能量和信息传递到越来越小的涡旋中，直到能量和信息都在波动的混乱中消失为止。 应当清楚地了解到，只有在系统不稳定或系统处于分叉或灾难边缘时，小的偏差才会导致系统的根本重组-这就是用数学语言在系统中调用系统行为的全局变化，而参数却有很小的变化。 分叉总是在参数空间中形成零度量集-它们是点或边界。 较小的干扰不会在几乎所有地方导致灾难（这也是一个精确的术语，意思是“除一组零度量值之外的所有地方”），自然界中不稳定的状态很少会通过“时间的考验”。

如果这对夫妻“因为废话”而分手，无论如何她注定要分手，那就很不稳定。 稳定的夫妻经历了战争和饥荒，然后有时分手，但这并不是因为琐事，而是由于一个人一生中可能发生的深刻变化。 在导致火车撞车的一系列事件中，很难挑出关键事件（特定的错误或致命事故），而且很可能关键不是事件，而是系统违反规则，导致系统进入不稳定状态。 如果系统中有很多参数，并且其中一些参数是随机的，并且我们的生活是这样构成的，那么这样的系统中的信息就容易丢失，并且不可能在我们生命中的确切时刻恢复“一切都出错了”。 不要为发生的事情感到后悔折磨自己，而要仔细看一下现在发生的事情，以免错过真正的分歧。

在这方面，我们可以回想起一种形态学定律，这被某些德雷森称为恢复定律 ：

改善状况的时间与恶化时间成反比。

给出以下观察结果作为示例： 粘花瓶要比弄断花瓶花费更长的时间。 该定律出乎意料地准确描述了稳定系统弛豫过程的特征速率之间的关系，这可以通过递减的指数定律来描述。 $$$e ^ {-\ lambda t}$ 和线性系统中的不稳定系统中灾难性过程的发展速度-小扰动的指数增长 $$$e ^ {\ lambda t}$ 。 这些速度确实彼此成反比。 但是，花瓶的例子并不是放松，而是过渡到最可能的状态。 它更接近另一个过程- 自组织 ，这个过程是逻辑定律描述的第一近似，与放松相比，与灾难相比更接近放松。

典型的非平稳过程：灾难，放松和自组织，具有相同的特征时间。

$$

$$* * *$$

有时候，我在雪地里行走，惊讶于雪花飘落在我的鼻子上。 令我惊讶的是，这一事件的可能性微乎其微。 从它的角度来看，她出生在太平洋上空高高的天空中，在云层中湍急的湍流中盘旋，跌落的方向不断变化……直达我的鼻尖！ 光子从遥远的恒星发出的光亮路径是什么！ 几万年来，它们冲过宇宙，没有被尘土吞没，没有遇到小行星！ 他们出生在遥远恒星的量子世界中，并在我眼中视网膜上视蛋白蛋白质的量子世界中结束了他们的旅程。 即使考虑到该事件的可能性也没有任何意义，它为零，但是该事件发生了，我看到一颗星星闪烁的光芒。 现在很明显，这全是因为我的鼻子甚至分子的面积都具有非零的量度，但仍然令人惊奇：几乎肯定不应该发生的事情还在发生！

让哲学家争论一下预定的或偶然的命运，我们对自然知识的真理或幻象。 我敦促读者从数学抽象的高度看待世界，并欣赏它的美丽和一致性。