合并按照以下原则对工作进行排序:
- 搜索有序的子数组(作为一个选项-形成)。
- 有序子数组被串联到一个公共有序子数组中。
就其本身而言,数组内部的任何有序子数组都没有太大价值。 但是,如果在一个数组中找到
两个有序的子数组,那么这是完全不同的事情。 事实是,您可以非常快速且低成本地合并它们-从一对有序子数组中形成一个常规有序子数组。

如您所见,将两个有序数组组合为一个并不容易,但非常简单。 您需要在两个数组中从左到右同时移动,并比较两个数组中的下一对元素。 较小的元素被发送到普通锅炉。 当元素以数组之一结尾时,另一个数组中的其余元素仅按顺序传输到主列表。
这是此类算法的精髓。 最初,随机数组可以分为许多小的有序子数组。 在成对合并中,有序子数组的数量减少,每个子数组的长度都增加。 在最后一步,该数组仅包含两个有序子数组,这些子数组合并为一个有序结构。

这个概念的作者是约翰·冯·诺伊曼。 有时有争议的说法是他在曼哈顿项目上工作时就提出了分类要求,因为他面临着在核弹研制过程中提供对大量统计数据进行有效计算的任务。 很难评估这个版本的合理性,因为他的第一本关于合并排序的工作可以追溯到1948年,炸弹的创建是在3年前完成的。 但是,有什么样的原子排序,让我们来看一下。
自然诺伊曼融合
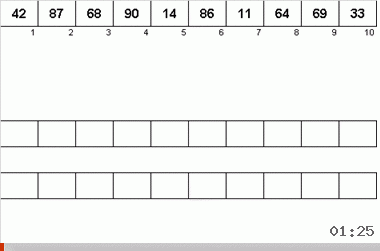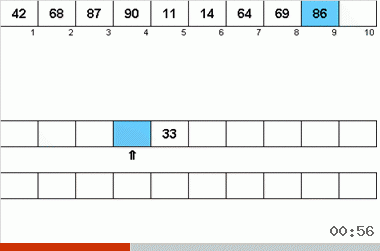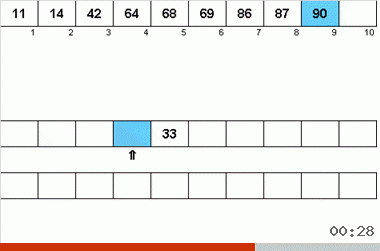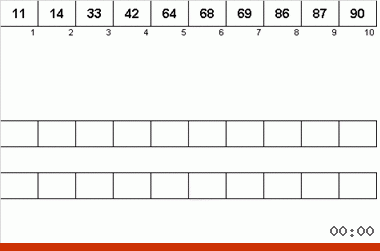
Neyman算法受40年代计算机设计特征的影响。 它看起来像这样:
- 总共使用了三种磁带-主磁带,其中记录了未分类的数据和两个辅助数据。
- 从主磁带顺序读取数据。
- 虽然顺序读取的数据是有序的子阵列,但它们会被复制到辅助磁带之一。
- 一旦完成下一个排序的子阵列(即,在主磁带上找到小于前一个元素的元素),便会在辅助磁带(子阵列的末端)上放置一个指针,并切换到另一个辅助磁带。
- 再次重复点2-4,仅将数据传输到另一个辅助磁带。 在下一个有序子阵列的末尾,主磁带交替切换到一个辅助磁带,然后切换到另一个。
- 读取完主磁带上的所有数据后,将进行辅助磁带的处理。
- 两个辅助磁带依次读取数据。
- 在这种情况下,将两个磁带的下一个数据相互比较。 根据比较结果,该对中最小的元素记录在主磁带上。
- 由于辅助磁带上阵列的边界用指针标记,因此读取和比较仅在已排序的子阵列内进行。
- 如果在一个辅助磁带上,下一个子阵列的元素已结束,则从其余磁带上将子阵列的其余部分简单地转移到主磁带上。
- 我们再次重复整个过程,直到主磁带上的数据为完全有序的阵列。
Neumann排序是一种自适应算法:它不仅固定数组的排序部分,而且首先尝试增加它们的大小,以便在细长的有序子数组的基础上形成甚至更长的有序子数组。 因此,它也称为
自适应合并排序 。
该算法的复杂度适中-O(
n 2 ),但是,对于管计算的先驱来说,这是一个突破。
在第一个合并排序的示例中,此类算法的缺点已经很明显-额外内存的成本。 在这方面,几乎所有合并排序都需要O(
n ),但是,很少有例外。
Bowes-Nelson直接合并
严格来说,Bowes-Nelson算法是一个排序网络,而不是排序。 在此过程中,将数组及其所有子数组分为两半,没有什么可以阻止所有这些一半在所有阶段并行处理。 但是,它也可以以排序的形式表示。 我们还将讨论网络排序的主题。

- 数组分为两半-分为左半部分和右半部分。
- 元素分为几组。
- 在第一次迭代中,这是两个元素(左半部分的第一个元素+右半部分的第一个元素,左半部分的第二个元素+右半部分的第二个元素,依此类推),第二个迭代-四个元素(1-左半部分的第二和第二元素+右半部分的第一和第二元素,左半部分的第三和第四元素+右半部分的第三和第四元素,依此类推),在第三部分-八岁等等
- 左半部分的每个组的元素都是排序的子数组,右半部分的每个组的元素也是排序的子数组。
- 合并上一段中排序后的子数组。
- 返回点1。循环继续进行,直到组的大小小于数组的大小为止。
似乎这里需要额外的内存。 但是不! 为了使动画更容易理解,将阵列的左半部分和右半部分彼此相对放置,以便比较的子阵列的相对位置更加明显。 但是,由于严格的二等分法,在不涉及内存中额外资源的情况下,可以进行所有比较和交换的算法。 这对于合并排序非常不常见。
def bose_nelson(data): m = 1 while m < len(data): j = 0 while j + m < len(data): bose_nelson_merge(j, m, m) j = j + m + m m = m + m return data def bose_nelson_merge(j, r, m): if j + r < len(data): if m == 1: if data[j] > data[j + r]: data[j], data[j + r] = data[j + r], data[j] else: m = m // 2 bose_nelson_merge(j, r, m) if j + r + m < len(data): bose_nelson_merge(j + m, r, m) bose_nelson_merge(j + m, r - m, m) return data
所有分选合并中都有某些东西使它们类似于氢弹。 首先发生分裂,然后进行合成。
参考文献
 合并
合并 /
合并系列文章:
今天的文章中提到的两种排序现在都可以在AlgoLab应用程序中使用(对于那些使用此Excel应用程序研究算法的人,请更新文件)。 在短短的几天内,随着即将发布的关于合并排序的续集的发布,将提供更多此类的算法。
Bowes-Nelson排序有一个限制-数组的大小必须为2的幂。 如果不满足此条件,则宏将裁剪数组到合适的大小。

本文是在EDISON Software的支持下编写的,该公司编写3D重建软件并正在开发复杂的测量设备 。