需要更多不同的模糊

使用高斯模糊滤镜的图像模糊广泛用于各种任务。 但是有时候在所有情况下，您都需要比仅一个过滤器更多的变化，在这种情况下，只有一个参数可以调整-它的大小。 在本文中，我们将介绍其他几种模糊实现。

引言

高斯模糊效果是线性运算，在数学上表示图像与滤波器矩阵的卷积。 在这种情况下，图像中的每个像素将替换为以某些加权因子拍摄的附近像素的总和。

过滤器之所以称为“高斯”，是因为它是根据称为“高斯”的函数构建的， $$$e ^ {-x ^ 2}$ ：



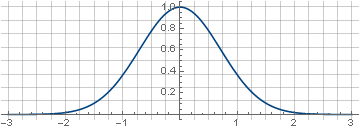
其二维形式是通过绕纵坐标轴旋转而获得的， $$$e ^ {-（x ^ 2 + y ^ 2）}$ ：



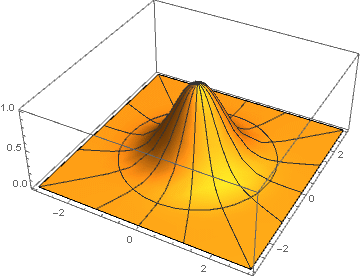
这里是每对坐标 $$$（x，y）$ 到中心的距离由公式计算 $$$\ sqrt {x ^ 2 + y ^ 2}$ ，它作为参数传递给高斯函数-并且，您可以轻松地看到， $$$e ^ {-\左（\ sqrt {x ^ 2 + y ^ 2} \右）^ 2}$ 减少到 $$$e ^ {-（x ^ 2 + y ^ 2）}$ 。

基于细分的矩阵 $$$[-3.3]$ 并进行一定程度的采样，结果将如下所示：

$$

$$\ left（\ begin {array} {ccccccc} 1.52 \乘以10 ^ {-8}＆2.26 \乘以10 ^ {-6}＆0.0000454＆0.000123＆0.0000454＆2.26 \乘以10 ^ {-6}＆1.52 \乘以10 ^ {-8} \\ 2.26 \乘以10 ^ {-6}＆0.000335＆0.00674＆0.0183＆0.00674＆0.000335＆2.26 \乘以10 ^ {-6} \\ 0.0000454＆0.00674＆0.135＆0.368＆0.135 ＆0.00674＆0.0000454 \\ 0.000123＆0.0183＆0.368＆1.00＆0.368＆0.0183＆0.000123 \\ 0.0000454＆0.00674＆0.135＆0.368＆0.135＆0.00674＆0.0000454 \\ 2.26 \次10 ^ {-6}＆0.000335＆0.00674＆ 0.0183＆0.00674＆0.000335＆2.26 \倍10 ^ {-6} \\ 1.52 \倍10 ^ {-8}＆2.26 \倍10 ^ {-6}＆0.0000454＆0.000123＆0.0000454＆2.26 \倍10 ^ { -6}＆1.52 \ times 10 ^ {-8} \\ \ end {array} \ right）$$

或者，如果我们将矩阵元素的值视为亮度级别，如下所示：



在信号处理方面，这称为脉冲响​​应，因为这是该滤波器与单个脉冲（在这种情况下为像素）的卷积结果的外观。

最初，高斯是在无限间隔上定义的。 但是由于其衰减很快，因此有可能从计算中排除接近零的值-因为它们仍然不会影响结果。 在实际应用中，还必须进行值归一化，以使在卷积后图像亮度不会改变。 并且在使每个像素具有相同颜色的图像模糊的情况下，图像本身不应更改。

为方便起见，通过引入附加参数，标准化也常用于坐标中 $$$\ sigma$ （读为“ sigma”）-考虑范围内的一个参数 $$$[-1,1]$ 和 $$$\ sigma$ 确定高斯的压缩率：

$$

$$\ frac {e ^ {-\ frac {x ^ 2 + y ^ 2} {2 \ sigma ^ 2}}} {2 \ pi \ sigma ^ 2}$$

归一化除法器 $$$2 \ pi \ sigma ^ 2$ 通过无穷大处的定积分解析式获得：

$$

$$\ int _ {-\ infty} ^ {\ infty} \ int _ {-\ infty} ^ {\ infty} e ^ {-\ frac {x ^ 2 + y ^ 2} {2 \ sigma ^ 2}} \， dx dy = 2 \ pi \ sigma ^ 2$$

由于平等的事实 $$$e ^ {-\左（x ^ 2 + y ^ 2 \右）} = e ^ {-x ^ 2} e ^ {-y ^ 2}$ 高斯模糊可以依次实现，首先在行中然后在列中进行-这可以使您节省大量计算时间。 在这种情况下，有必要针对一维情况使用归一化公式-

$$

$$\ frac {e ^ {-\ frac {x ^ 2} {2 \ sigma ^ 2}}} {\ sqrt {2 \ pi \ sigma ^ 2}}$$

开始

对于任意滤波器，我们首先需要根据一个变量定义自己的衰减函数 $$$f$ ，通过替换从中获得两个变量的函数 $$$x$ 在 $$$\ sqrt {x ^ 2 + y ^ 2}$ 在哪里 $$$x$ 和 $$$y$ 这些是范围内矩阵元素的坐标 $$$（-1,1）$ ，然后将其用于填充矩阵的元素。 归一化将不会被分析地考虑，而是矩阵所有元素的直接求和-这既简单又准确-因为离散化后函数会“变薄”，并且归一化值将取决于离散化程度。

如果矩阵元素是从头开始编号的，则坐标 $$$x$ 或 $$$y$ 由公式计算

$$

$$\ frac {2索引} {size-1} -1$$

在哪里 $$$索引$ -行或列中元素的序列号，以及 $$$大小$ -元素总数。

例如，对于5 x 5矩阵，它看起来像这样：

$$

$$\左（\ begin {array} {ccccc} f（-1，-1）＆f \左（-\ frac {1} {2}，-1 \ right）＆f（0，-1）＆f \左（\ frac {1} {2}，-1 \右）＆f（1，-1）\\ f \左（-1，-\ frac {1} {2} \ right）＆f \左（-\ frac {1} {2}，-\ frac {1} {2} \ right）＆f \ left（0，--\ frac {1} {2} \ right）＆f \ left（\ frac { 1} {2}，-\ frac {1} {2} \ right）和f \ left（1，-\ frac {1} {2} \ right）\\ f（-1.0）＆f \ left （-\ frac {1} {2}，0 \右）＆f（0,0）＆f \左（\ frac {1} {2}，0 \右）＆f（1,0）\\ f \左（-1，\ frac {1} {2} \右）＆f \左（-\ frac {1} {2}，\ frac {1} {2} \右）＆f \左（0， \ frac {1} {2} \ right）和f \ left（\ frac {1} {2}，\ frac {1} {2} \ right）＆f \ left（1，\ frac {1} {2 } \ right）\\ f（-1,1）＆f \ left（-\ frac {1} {2}，1 \ right）＆f（0,1）＆f \ left（\ frac {1} { 2}，1 \ right）＆f（1,1）\\ \ end {array} \ right）$$

或者，如果我们排除仍然为零的边界值，则坐标将通过公式计算

$$

$$\ frac {2 index-size + 1} {size}$$

矩阵将相应地采用以下形式

$$

$$\ left（\ begin {array} {ccccc} f \ left（-\ frac {4} {5}，-\ frac {4} {5} \ right）和f \ left（-\ frac {2} { 5}，-\ frac {4} {5} \ right）＆f \左（0，-\ frac {4} {5} \ right）＆f \ left（\ frac {2} {5}，-\ frac {4} {5} \ right）和f \ left（\ frac {4} {5}，-\ frac {4} {5} \ right）\\ f \ left（-\ frac {4} {5 }，-\ frac {2} {5} \ right）和f \ left（-\ frac {2} {5}，-\ frac {2} {5} \ right）＆f \ left（0，-\ frac {2} {5} \ right）和f \ left（\ frac {2} {5}，-\ frac {2} {5} \ right）＆f \ left（\ frac {4} {5}， -\ frac {2} {5} \ right）\\ f \左（-\ frac {4} {5}，0 \ right）＆f \ left（-\ frac {2} {5}，0 \ right ）＆f（0,0）＆f \左（\ frac {2} {5}，0 \右）＆f \左（\ frac {4} {5}，0 \右）\\ f \左（ -\ frac {4} {5}，\ frac {2} {5} \ right）和f \左（-\ frac {2} {5}，\ frac {2} {5} \ right）和f \左（0，\ frac {2} {5} \右）＆f \左（\ frac {2} {5}，\ frac {2} {5} \右）＆f \左（\ frac {4} {5}，\ frac {2} {5} \ right）\\ f \ left（-\ frac {4} {5}，\ frac {4} {5} \ right）＆f \ left（-\ frac {2} {5}，\ frac {4} {5} \ right）和f \ left（0，\ frac {4} {5} \ right）＆f \ left（\ frac {2} {5}， \ frac {4} {5} \ right）和f \ left（\ frac {4} {5}，\ frac {4} {5} \ right）\\ \ end {array} \ right）$$

通过公式计算矩阵元素之后，有必要计算它们的总和并将矩阵除以它。 例如，如果我们得到一个矩阵

$$

$$\左（\开始{array} {ccc} 1＆4＆1 \\ 4＆20＆4 \\ 1＆4＆1 \\ \ end {array} \ right）$$

则所有元素的总和为40，归一化后的形式为

$$

$$\ left（\ begin {array} {ccc} \ frac {1} {40}＆\ frac {1} {10}＆\ frac {1} {40} \\ \ frac {1} {10}＆\ frac {1} {2}＆\ frac {1} {10} \\ \ frac {1} {40}＆\ frac {1} {10}＆\ frac {1} {40} \\ \ end {array } \对）$$

其所有元素的总和为1。

线性衰减

首先，采用最简单的功能-该行：

$$

$$\左\ {\开始{array} {ll} 1-x，＆x <1 \\ 0，＆x \ geqslant 1 \\ \ end {array} \ right$$

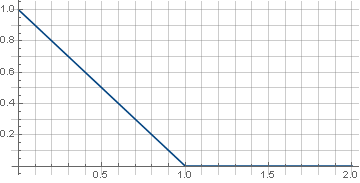
此处的分段连续定义要求函数必须保证为零，并且在旋转过程中在矩阵的角上不会出现伪影。 另外，由于旋转使用的坐标的平方和的根始终为正，因此仅在值的正部分确定函数就足够了。 结果，我们得到：

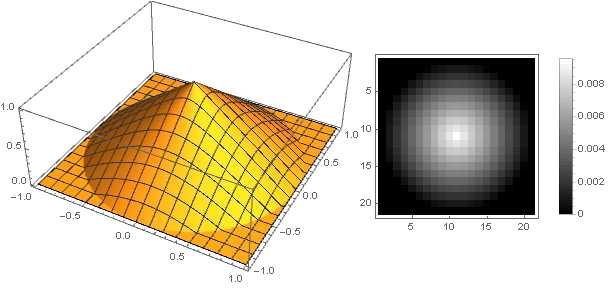
软线性衰减

从斜线到零功能的急剧过渡会引起矛盾，并带有美感。 为了解决这个问题，该功能将为我们提供帮助。

$$

$$1- \ frac {n x-x ^ n} {n-1}$$

在其中 $$$n$ 确定对接的“刚性”， $$$n> 1$ 。 举个例子 $$$n = 3$ 我们得到

$$

$$\左\ {\开始{array} {ll} 1- \ frac {3 xx ^ 3} {2}，＆x <1 \\ 0，＆x \ geqslant 1 \\ \ end {array} \ right。$$

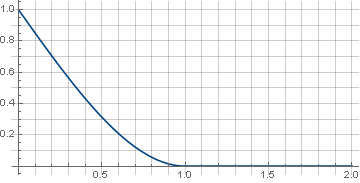
过滤器本身看起来像

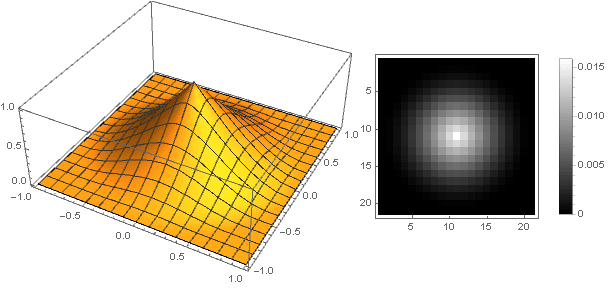
双曲衰减

通过采用另一个函数（例如，双曲线），并通过与抛物线求和，可以确保平滑地过渡到零，从而使滤波器更“锐利”并且更平滑地趋于零。



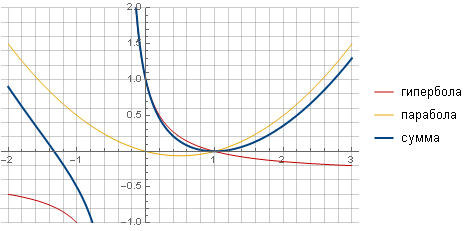
经过所有的计算和简化，我们得出公式

$$

$$\ left \ {\ begin {array} {ll} \ frac {（x-1）^ 2（k x + k + 1）} {（k + 1）（k x + 1）}，＆x <1 \\ 0和＆x \ geqslant 1 \\ \ end {array} \对$$

在哪个参数 $$$k> 0$ 确定衰减的性质：



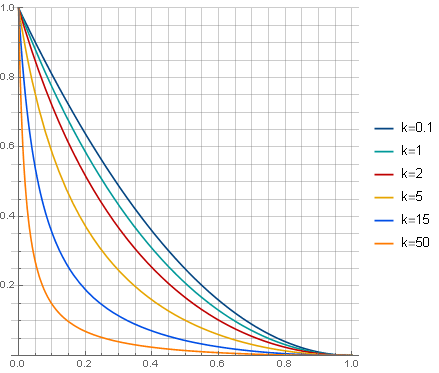
过滤器本身看起来（ $$$k = 5$ ）如何

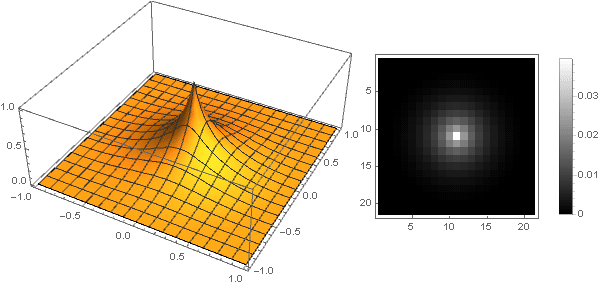
散景效果

您可以采取另一种方法-使过滤器的顶部不尖锐，但很愚蠢。 实现此目的的最简单方法是将阻尼功能设置为常数：

$$

$$\左\ {\开始{array} {ll} 1，＆x <1 \\ 0，＆x \ geqslant 1 \\ \ end {array} \ right。$$

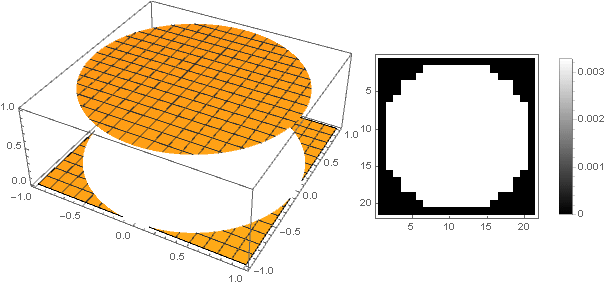
但是在这种情况下，我们得到了很强的像素感，这与美感形成了鲜明的对比。 为了使它的边缘更平滑，高阶抛物线将为我们提供帮助，通过沿纵坐标轴移动它并平方，可以得到

$$

$$\ left \ {\ begin {array} {ll} \ left（1-x ^ n \ right）^ 2，＆x <1 \\ 0，＆x \ geqslant 1 \\ \ end {array} \ right。$$

可变参数 $$$n$ 您可以获得各种各样的过滤器选项：

$$

$$n = 0.5$$

$$

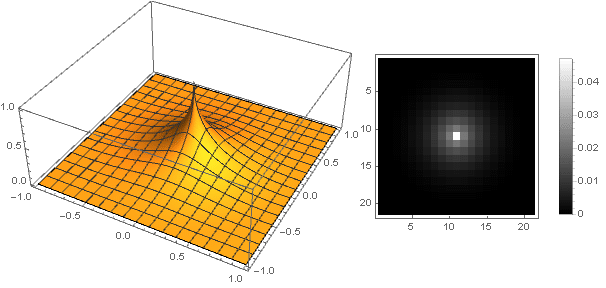
$$n = 2$$

$$

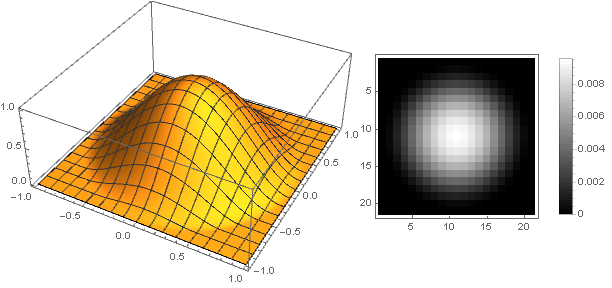
$$n = 10$$

$$

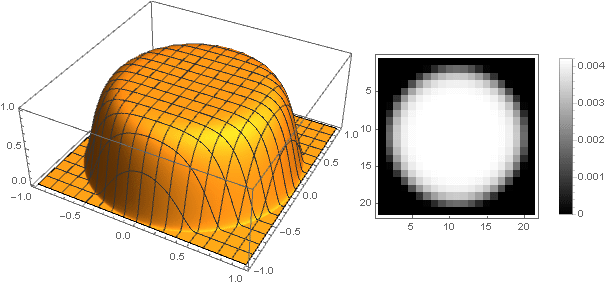
$$n = 50$$

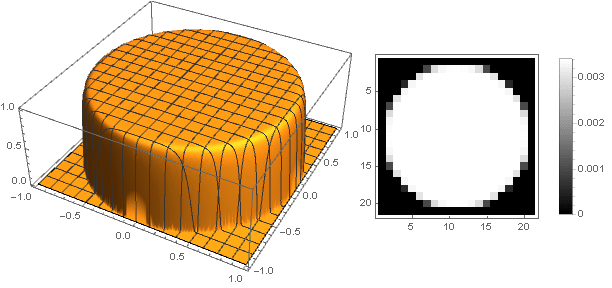
通过稍微修改阻尼功能，可以使滤镜边缘的环更明显，例如：

$$

$$\左\ {\开始{array} {ll} \左（1-x ^ n \右）^ 2 \左（d + x ^ m \右），＆x <1 \\ 0，＆x \ geqslant 1 \\ \ end {array} \对$$

这里参数 $$$d$ 确定中心的高度，并 $$$m$ -过渡到边缘的清晰度。
对于 $$$d = 0.2，m = 2，n = 10$ 我们得到



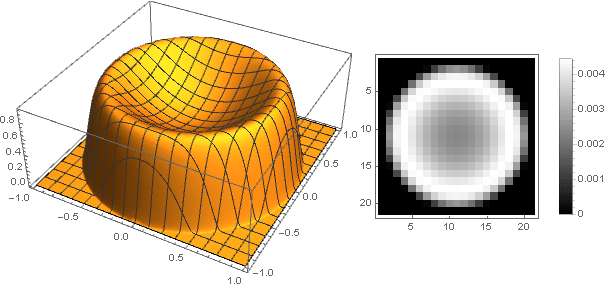
但是为了 $$$d = 0，m = 12，n = 2$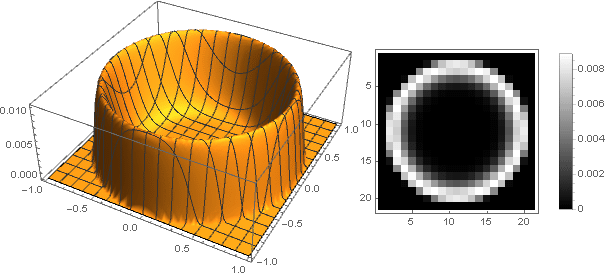

高斯变异

高斯本身的功能也可以直接修改。 最明显的方法是对指数进行参数化-我们现在不考虑它，但采取更有趣的选择：

$$

$$\ left \ {\ begin {array} {ll} e ^ {\ frac {kx ^ 2} {x ^ 2-1}}，＆-1 <x <1 \\ 0，否则，\\ \ end {数组} \对$$

由于事实与 $$$x$ 单位分母 $$$x ^ 2-1$ 倾向于零分数 $$$\ frac {k x ^ 2} {x ^ 2-1}$ 趋于负无穷大，指数本身也趋于零。 因此除以 $$$x ^ 2-1$ 允许使用压缩功能定义的域 $$$（-\ infty，\ infty）$ 之前 $$$（-1,1）$ 。 而且，什么时候 $$$x = \ pm 1$ 由于除以零（ $$$1 ^ 2-1 = 0$ ）函数的值未定义，但有两个限制-一方面（从内部）的限制为零，另一方面，无穷大：

$$

$$\ underset {x \到1 ^-} {\ text {lim}} e ^ {\ frac {k x ^ 2} {x ^ 2-1}} = 0$$

$$

$$\ underset {x \到1 ^ +} {\ text {lim}} e ^ {\ frac {k x ^ 2} {x ^ 2-1}} = \ infty$$

由于边界值不包括在间隔中，因此仅在一侧的极限中为零就足够了。 有趣的是，此属性扩展到此函数的所有派生类，从而确保与零的完美匹配。

参量 $$$k$ 确定与高斯的相似度-数值越大，相似度越强-这是因为截面逐渐增加 $$$\ frac {1} {x ^ 2-1}$ 落在功能的中心。 可以假定，由于这个原因，在极限范围内，您可以得到原始的高斯函数-但是，不幸的是，没有-函数仍然不同。



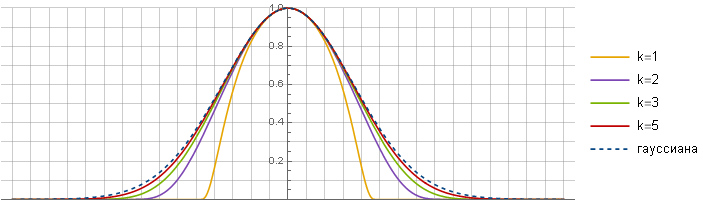
现在您可以看到发生了什么：

$$

$$k = 5$$

$$

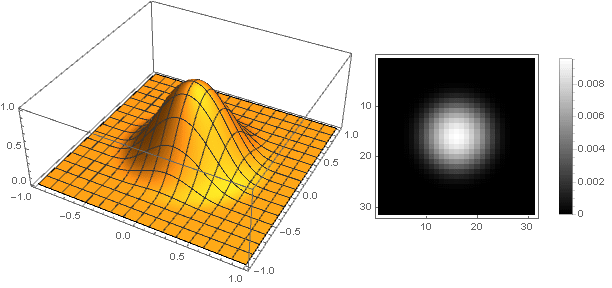
$$k = 2$$

$$

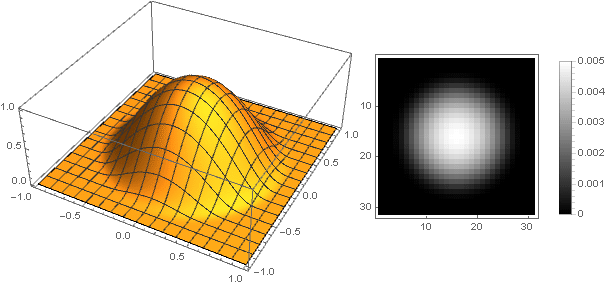
$$k = 0.5$$

$$

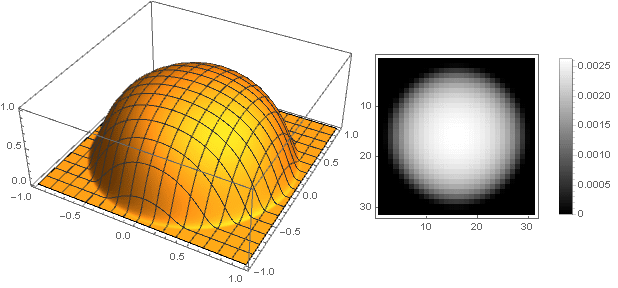
$$k = 0.1$$

$$

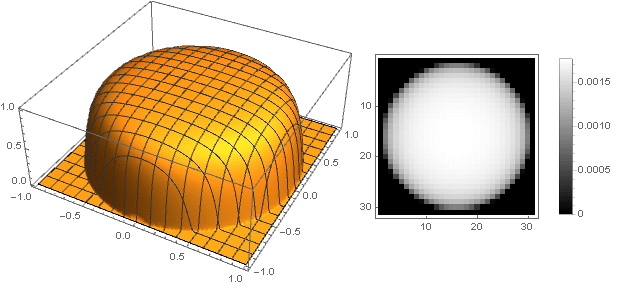
$$k = 0.01$$

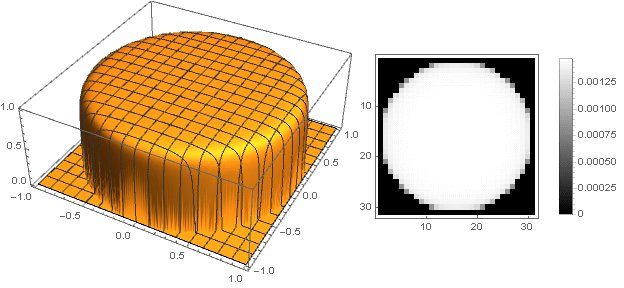
形状变化

通过将转换函数从两个坐标更改为一个 $$$\ sqrt {x ^ 2 + y ^ 2}$ ，您可以获得其他形状，而不仅仅是磁盘。 例如：

$$

$$f \左（\ frac {\左| x-y \右| + \左| x + y \右|} {2} \右）$$

$$

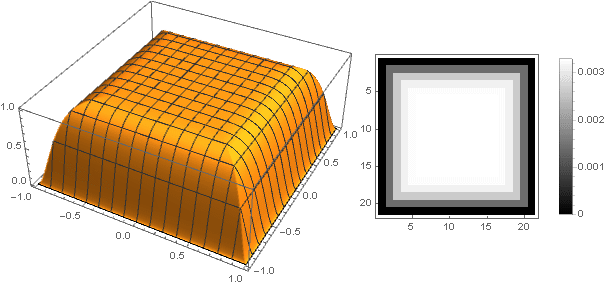
$$f（\左| x \右| + \左| y \右|）$$

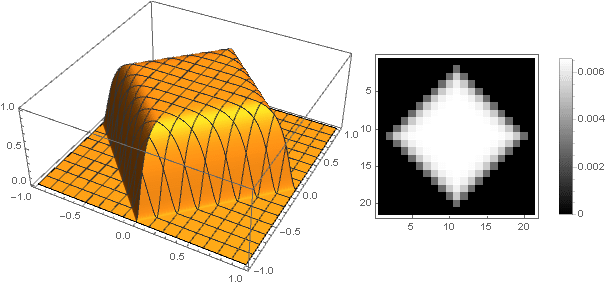
通过移至复数，可以构造更复杂的数字：

$$

$$f \左（\ frac {\左| \ Re \左（（x + iy）（-1）^ {\ frac {0} {3}} \右）\右| + \左| \ Re \左（（x + iy）（-1）^ {\ frac {1} {3}} \ right）\ right | + \ left | \ Re \ left（（x + iy）（-1）^ {\ frac { 2} {3}} \ right）\ right |} {\ sqrt {3}} \ right）$$

$$

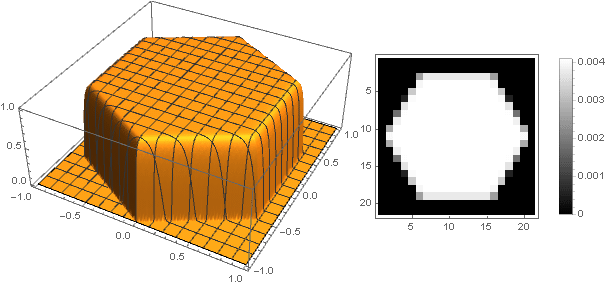
$$f \ biggl（10 \左| \ Re \左（（x + iy）（-1）^ {\ frac {1} {8}} \右）\右| \ biggr）\ cdot f（\左| x + iy \对|）$$

$$

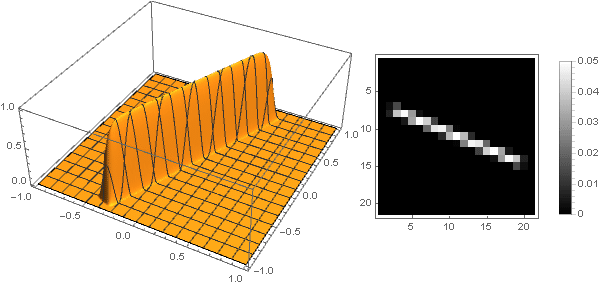
$$f \ biggl（\ biggl | 5 \左| x + iy \右|（x + iy）\ Re \ biggl（\ cos \左（\ frac {5} {2} \ arg（x + iy）\右）\ biggr）\ biggr | \ biggr）\ cdot f（\左| x + iy \右|）$$

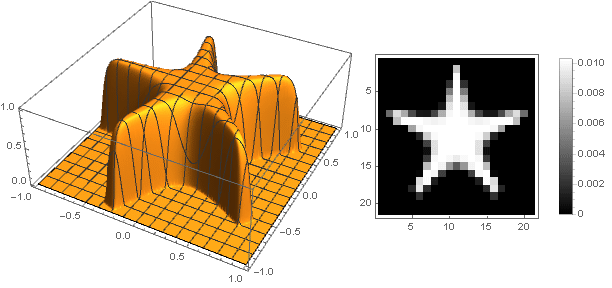
在这种情况下，必须确保在转换坐标时不要超出间隔 $$$（0,1）$ -好吧，反之亦然，请为参数的负值重新定义阻尼函数。

一些具体的例子

如果不对特定图像进行实际测试，则文章将是不完整的。 由于我们没有科学的工作，因此我们也不会采用Lena的形象-我们会做一些柔软蓬松的事情：


















相同的过滤器，但对于文本：

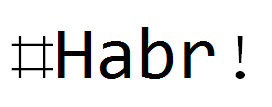
结论

同样，您可以构建更复杂的滤镜，包括带有锐化或轮廓的滤镜。 并修改已经考虑的内容。

当滤波器系数的值取决于坐标或直接被滤波的图像时，非线性滤波尤其令人关注，但这已经成为其他研究的主题。

更详细地， 这里考虑了用于与常数对接的函数的推导。 这里考虑的窗函数也可以用作衰减函数-所需要做的只是将参数c（0,1）缩放为（ $$$\ frac {1} {2}$ ，1）或最初通过公式考虑窗口函数 $$$\ frac {1} {2} \ left（f \ left（\ frac {t x + 1} {t-1} \ right）-f \ left（\ frac {t x-1} {t-1} \正确）\正确）$ 。

本文的Wolfram Mathematica源文档可以在这里下载。